Fuzzy Structural Analysis Michael Beer Dresden University of

Fuzzy Structural Analysis Michael Beer Dresden University of Technology Institute of Structural Analysis

Fuzzy Structural Analysis Introduction Basic problems Solution technique - -level optimization Examples Conclusions Dresden University of Technology Institute of Structural Analysis

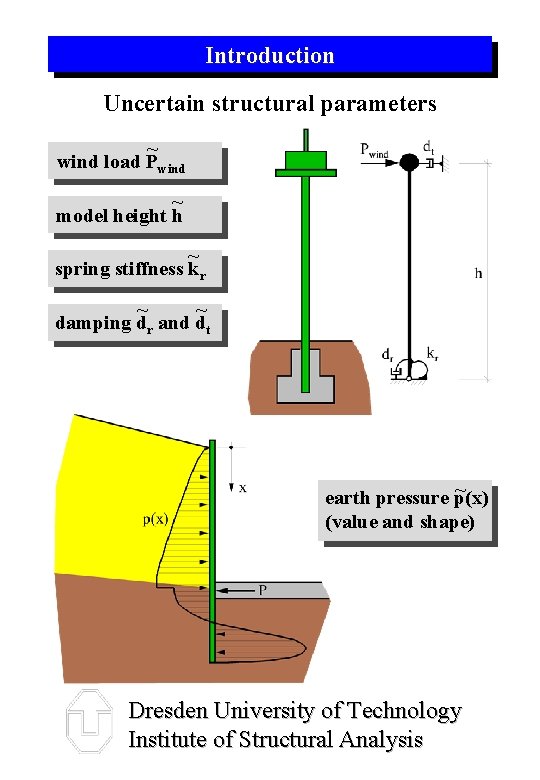
Introduction Uncertain structural parameters ~ wind load Pwind ~ model height h ~ spring stiffness kr ~ ~ damping dr and dt ~ earth pressure p(x) (value and shape) Dresden University of Technology Institute of Structural Analysis

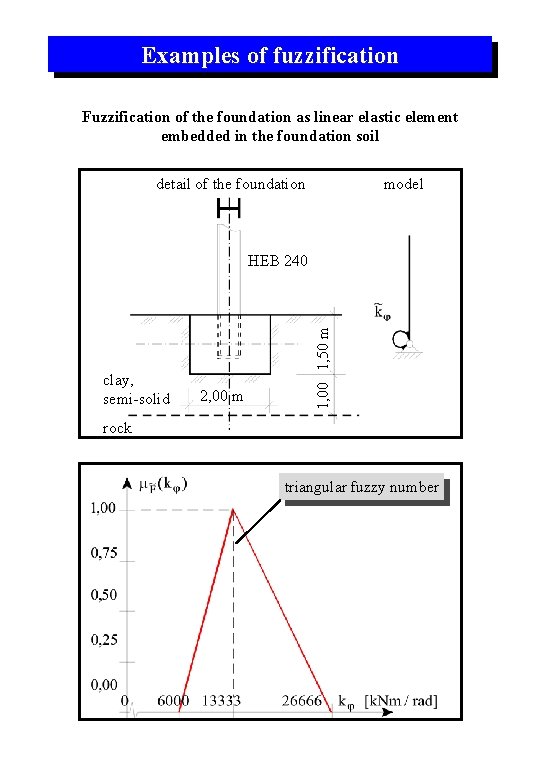
Examples of fuzzification Fuzzification of the foundation as linear elastic element embedded in the foundation soil detail of the foundation model clay, semi-solid 2, 00 m 1, 00 1, 50 m HEB 240 rock triangular fuzzy number

Examples of fuzzification Fuzzification of end-plate shear connections at the corner of a plane frame detail of the plane frame model IPE 330 HEB 240 triangular fuzzy number

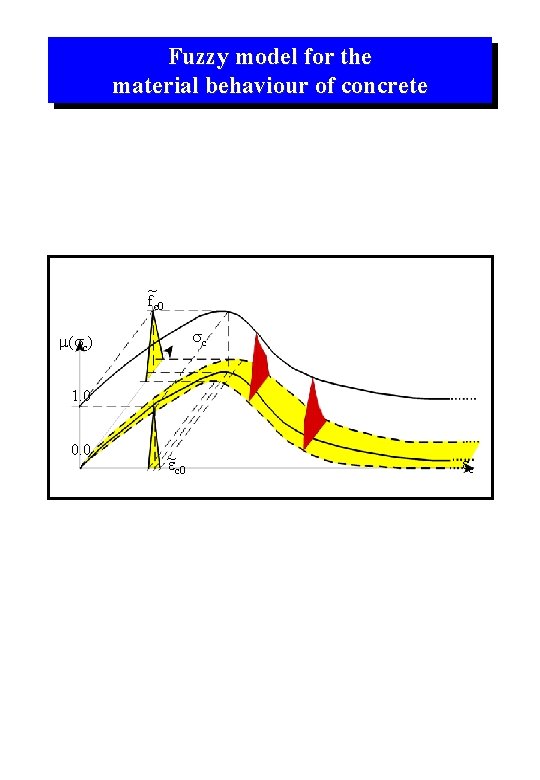
Fuzzy model for the material behaviour of concrete ~ fc 0 sc m(sc) 1. 0 0. 0 ~e c 0 ec

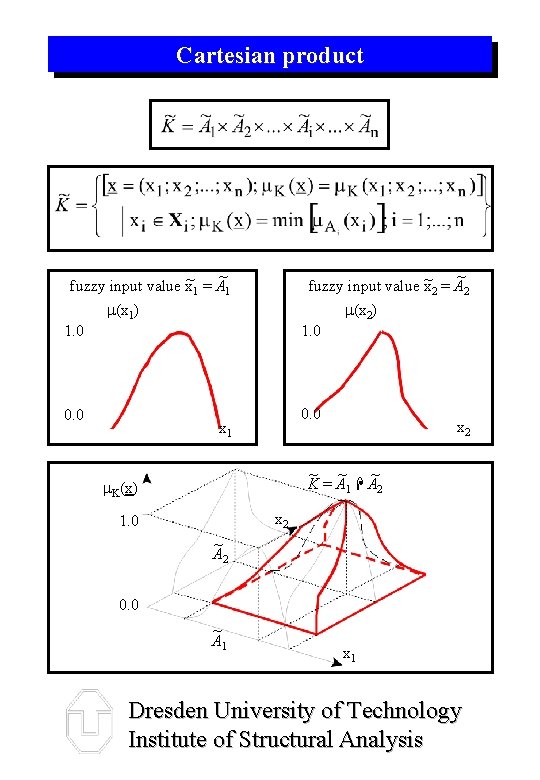
Cartesian product ~ fuzzy input value x~1 = A 1 m(x 1) 1. 0 ~ fuzzy input value x~2 = A 2 m(x 2) 1. 0 0. 0 x 1 x 2 ~ ~ ~ K = A 1 A 2 m. K(x) x 2 1. 0 ~ A 2 0. 0 ~ A 1 x 1 Dresden University of Technology Institute of Structural Analysis

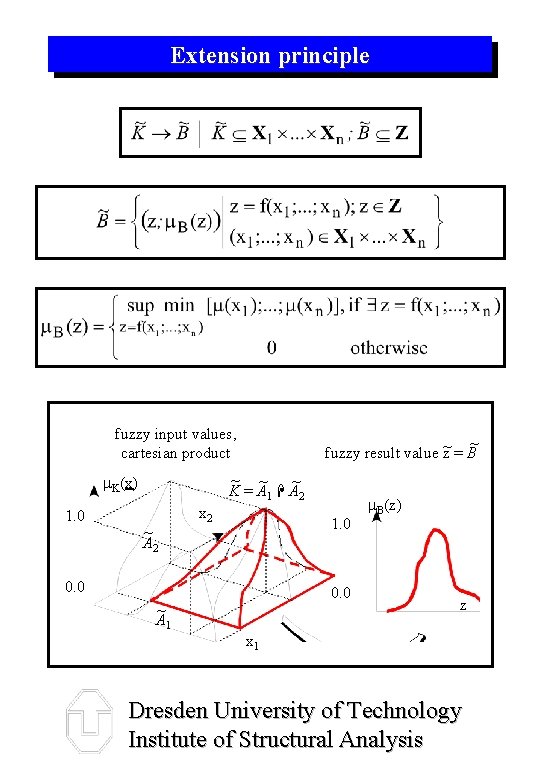
Extension principle fuzzy input values, cartesian product ~ ~ ~ K = A 1 A 2 m. K(x) 1. 0 ~ fuzzy result value z~ = B ~ A 2 x 2 1. 0 0. 0 ~ A 1 m. B(z) z x 1 Dresden University of Technology Institute of Structural Analysis

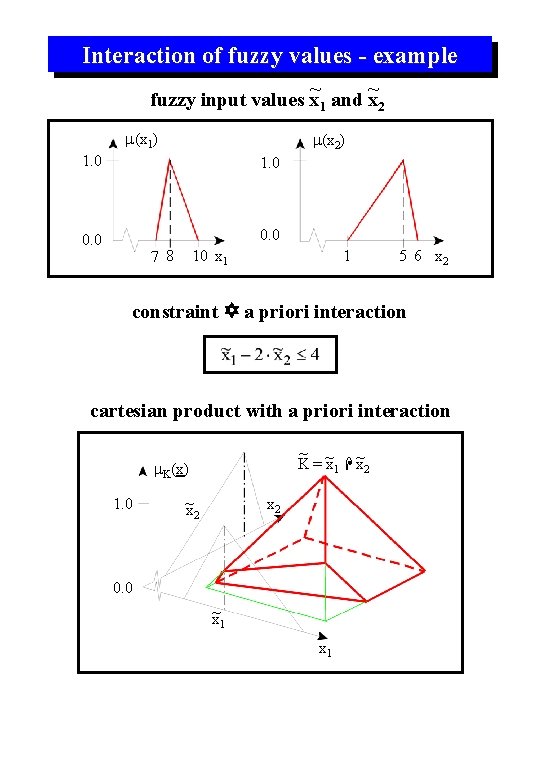
Interaction of fuzzy values - example ~ ~ fuzzy input values x 1 and x 2 m(x 1) m(x 2) 1. 0 0. 0 7 8 10 x 1 1 5 6 x 2 constraint a priori interaction cartesian product with a priori interaction ~ K = ~x 1 ~ x 2 m. K(x) 1. 0 ~ x 2 0. 0 ~ x 1

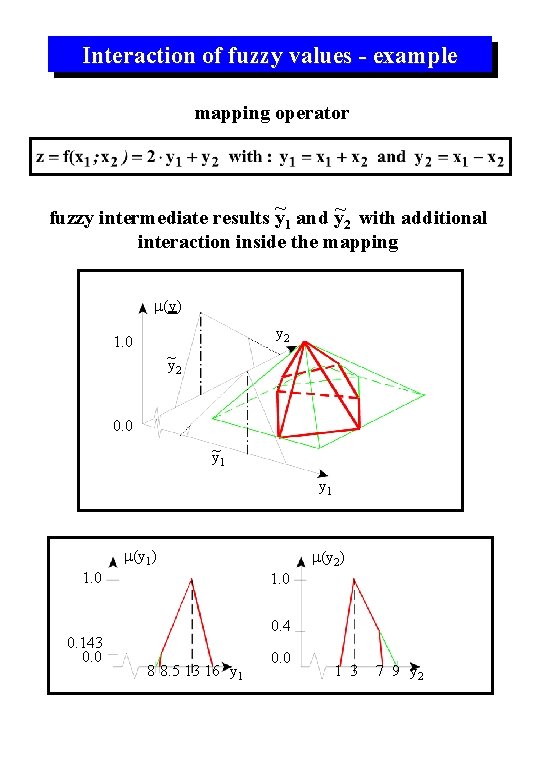
Interaction of fuzzy values - example mapping operator fuzzy intermediate results y~1 and y~2 with additional interaction inside the mapping m(y) y 2 1. 0 ~ y 2 0. 0 ~ y 1 m(y 1) 1. 0 0. 143 0. 0 m(y 2) 1. 0 0. 4 8 8. 5 13 16 y 1 0. 0 1 3 7 9 y 2

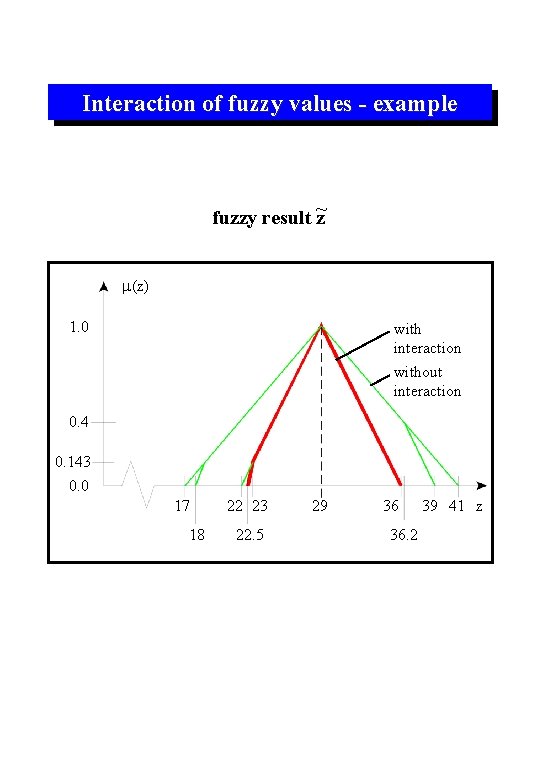
Interaction of fuzzy values - example fuzzy result ~z m(z) 1. 0 with interaction without interaction 0. 4 0. 143 0. 0 17 18 22 23 22. 5 29 36 36. 2 39 41 z

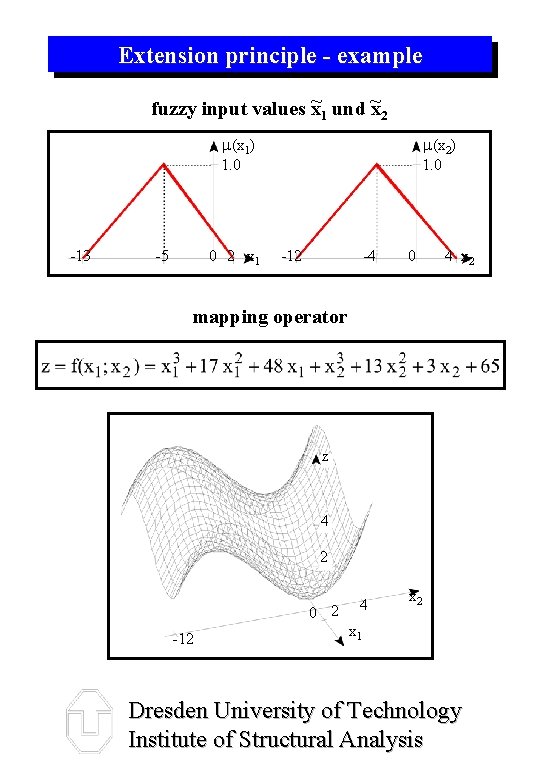
Extension principle - example fuzzy input values x~1 und ~x 2 m(x 1) 1. 0 -13 0 2 x 1 -5 m(x 2) 1. 0 -12 -4 0 4 x 2 mapping operator z 4 2 0 2 -12 x 1 Dresden University of Technology Institute of Structural Analysis

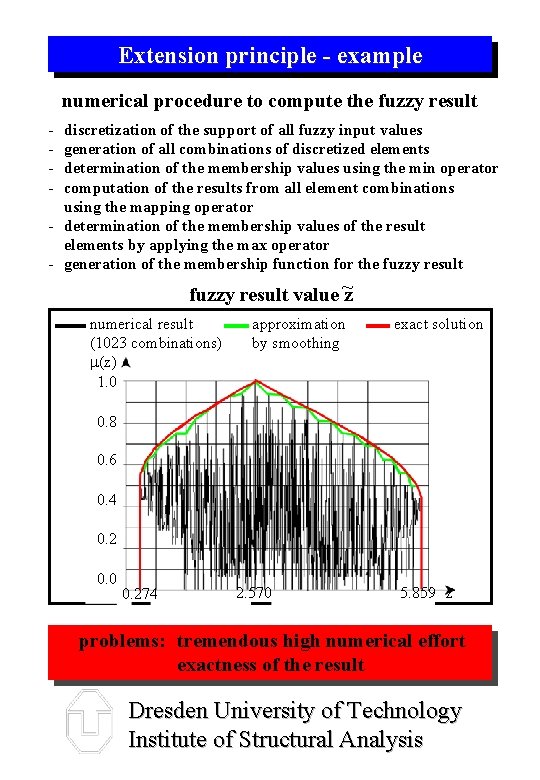
Extension principle - example numerical procedure to compute the fuzzy result - discretization of the support of all fuzzy input values generation of all combinations of discretized elements determination of the membership values using the min operator computation of the results from all element combinations using the mapping operator - determination of the membership values of the result elements by applying the max operator - generation of the membership function for the fuzzy result value ~z numerical result (1023 combinations) m(z) 1. 0 approximation by smoothing exact solution 0. 8 0. 6 0. 4 0. 2 0. 0 0. 274 2. 570 5. 859 z problems: tremendous high numerical effort exactness of the result Dresden University of Technology Institute of Structural Analysis

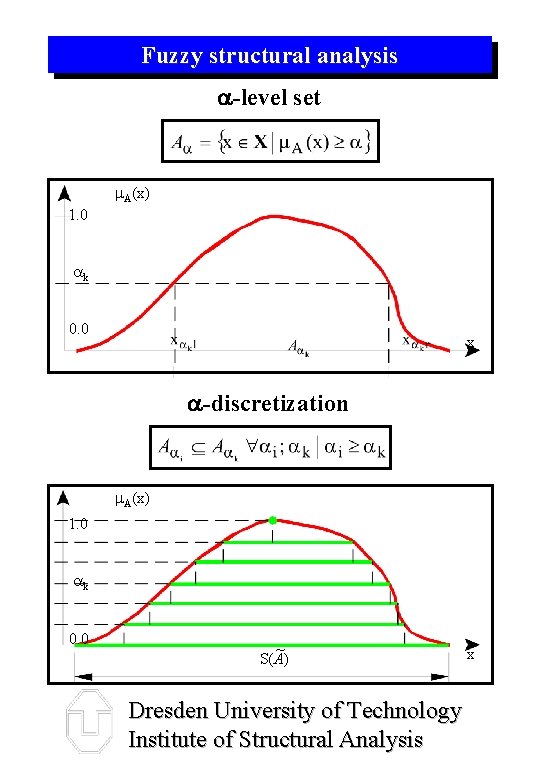
Fuzzy structural analysis -level set m. A(x) 1. 0 ak 0. 0 x -discretization m. A(x) 1. 0 ak 0. 0 ~ S(A) Dresden University of Technology Institute of Structural Analysis x

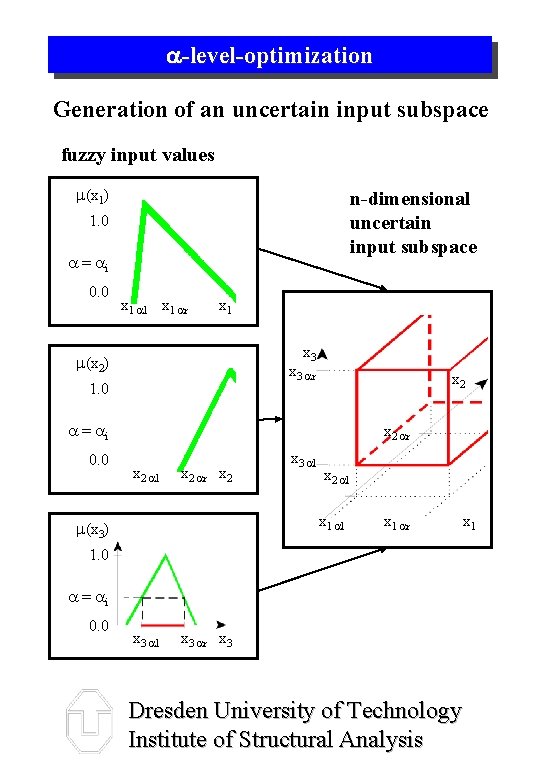
-level-optimization Generation of an uncertain input subspace fuzzy input values m(x 1) n-dimensional uncertain input subspace 1. 0 a = ai 0. 0 x 1 al x 1 ar x 1 x 3 m(x 2) x 3 ar 1. 0 x 2 a = ai 0. 0 x 2 ar x 2 al x 2 ar x 2 x 3 al x 2 al x 1 al m(x 3) x 1 ar x 1 1. 0 a = ai 0. 0 x 3 al x 3 ar x 3 Dresden University of Technology Institute of Structural Analysis

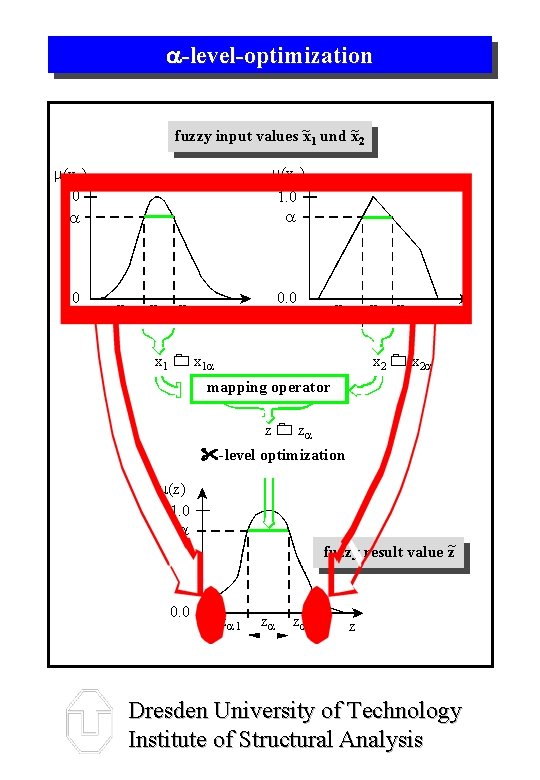
-level-optimization fuzzy input values ~x 1 und x~2 m(x 2) 1. 0 a m(x 1) 1. 0 a 0. 0 x 1 a l x 1 a r 0. 0 x 1 x 2 a l x 2 a r x 1 a x 2 a mapping operator z za -level optimization m(z) 1. 0 a 0. 0 fuzzy result value z~ za l za za r z Dresden University of Technology Institute of Structural Analysis

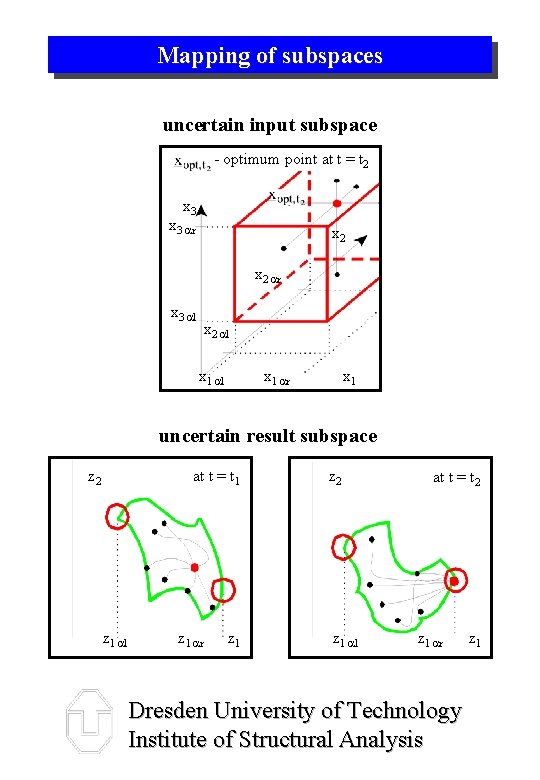
Mapping of subspaces uncertain input subspace - optimum point at t = t 2 x 3 ar x 2 ar x 3 al x 2 al x 1 ar x 1 uncertain result subspace at t = t 1 z 2 z 1 al z 1 ar z 1 z 2 z 1 al at t = t 2 z 1 ar Dresden University of Technology Institute of Structural Analysis z 1

-level-optimization fuzzy input values, uncertain input subspace optimization problem search for the optimum points xopt and computation of the assigned results zj objective functions zj = fj(x) (discrete set) are described by the mapping operator - no special properties, generally only implicit standard optimization methods are only partly suitable to solve the problem modified evolution strategy with elements of the Monte-Carlo method and the gradient method fuzzy result values Dresden University of Technology Institute of Structural Analysis

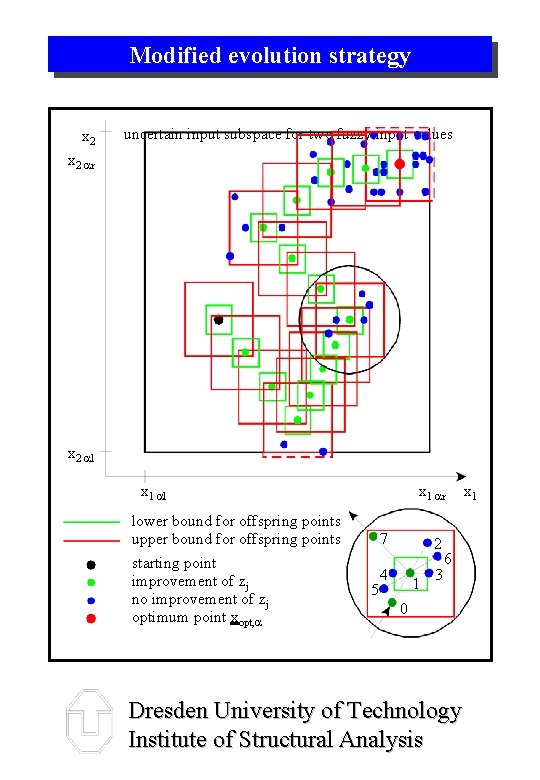
Modified evolution strategy x 2 uncertain input subspace for two fuzzy input values x 2 ar x 2 al x 1 al lower bound for offspring points upper bound for offspring points starting point improvement of zj no improvement of zj optimum point xopt, a x 1 ar 7 5 2 4 1 3 6 0 Dresden University of Technology Institute of Structural Analysis x 1

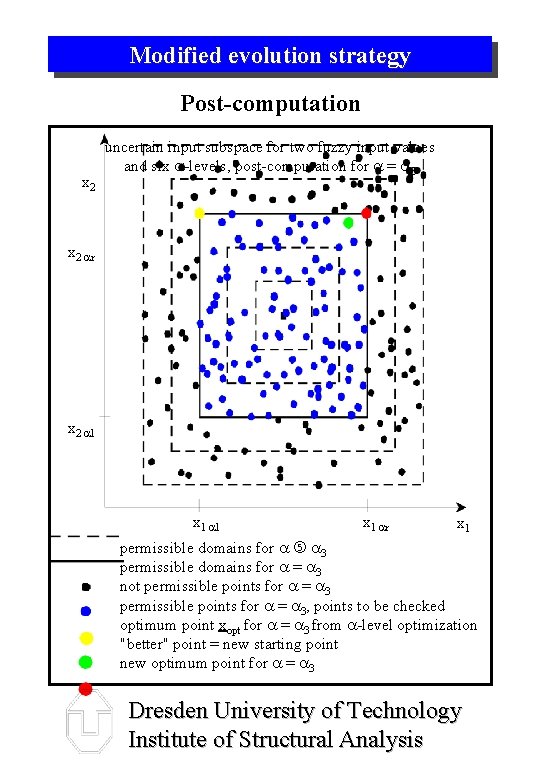
Modified evolution strategy Post-computation x 2 uncertain input subspace for two fuzzy input values and six a-levels, post-computation for a = a 3 x 2 ar x 2 al x 1 ar x 1 permissible domains for a a 3 permissible domains for a = a 3 not permissible points for a = a 3, points to be checked optimum point xopt for a = a 3 from a-level optimization "better" point = new starting point new optimum point for a = a 3 Dresden University of Technology Institute of Structural Analysis

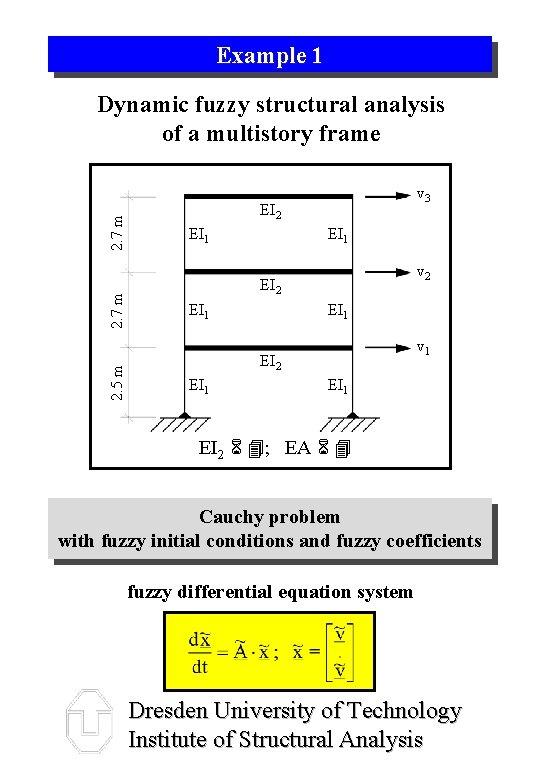
Example 1 2. 5 m 2. 7 m Dynamic fuzzy structural analysis of a multistory frame v 3 EI 2 EI 1 v 2 EI 1 v 1 EI 2 EI 1 EI 2 ; EA Cauchy problem with fuzzy initial conditions and fuzzy coefficients fuzzy differential equation system Dresden University of Technology Institute of Structural Analysis

Investigation I deterministic parameters EI 1 = 4 A 103 k. Nm 2 fuzzy damping parameters 1. 0 m(dii) 0. 5 0. 0 fuzzy initial conditions mapping operator Dresden University of Technology Institute of Structural Analysis dii

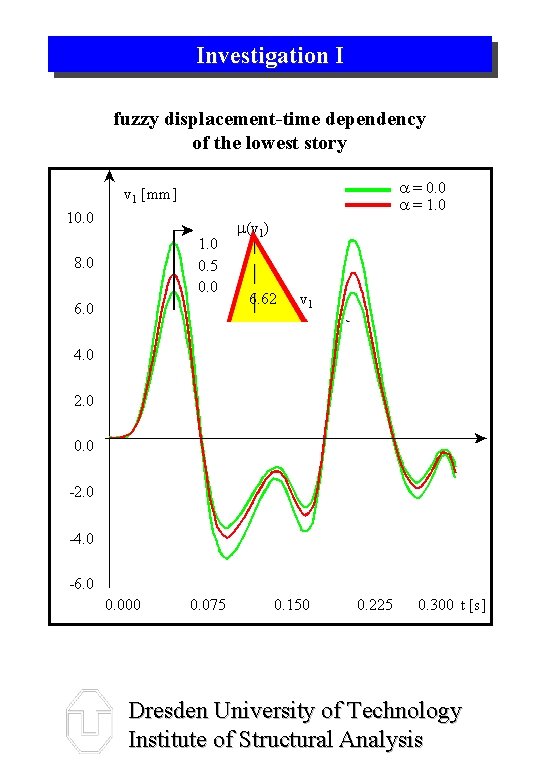
Investigation I fuzzy displacement-time dependency of the lowest story a = 0. 0 a = 1. 0 v 1 [mm] 10. 0 1. 0 0. 5 0. 0 8. 0 6. 0 m(v 1) 6. 62 v 1 4. 0 2. 0 0. 0 -2. 0 -4. 0 -6. 0 0. 000 0. 075 0. 150 0. 225 0. 300 t [s] Dresden University of Technology Institute of Structural Analysis

Investigation II I 1 = 1. 333 A 10 -4 m 4 deterministic parameters deterministic initial conditions deterministic dii = 0. 05 k. Nsm-1; i = 1; . . . ; 3 damping parameters fuzzy elastic modulus m(E) 1. 0 0. 5 0. 0 2. 7 A 107 3. 0 A 107 3. 2 A 107 E [k. Nm-2] mapping operator Dresden University of Technology Institute of Structural Analysis

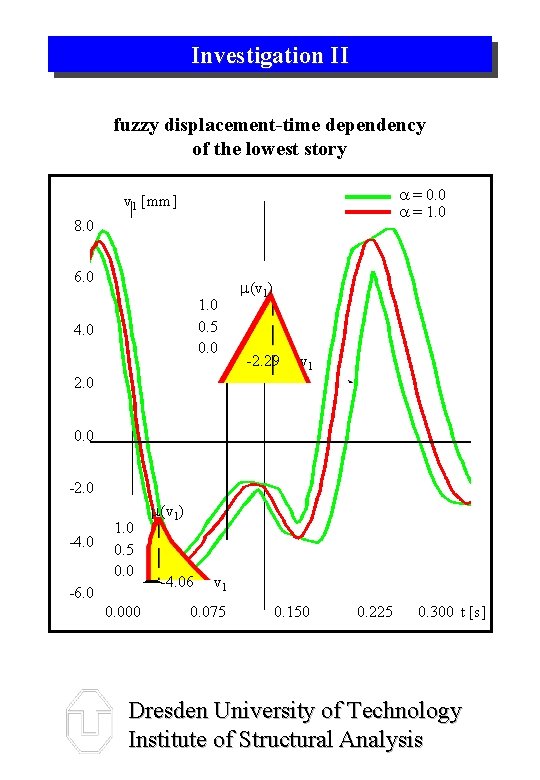
Investigation II fuzzy displacement-time dependency of the lowest story a = 0. 0 a = 1. 0 v 1 [mm] 8. 0 6. 0 1. 0 0. 5 0. 0 4. 0 m(v 1) -2. 29 v 1 2. 0 0. 0 -2. 0 -4. 0 1. 0 0. 5 0. 0 -6. 0 0. 000 m(v 1) -4. 06 v 1 0. 075 0. 150 0. 225 0. 300 t [s] Dresden University of Technology Institute of Structural Analysis

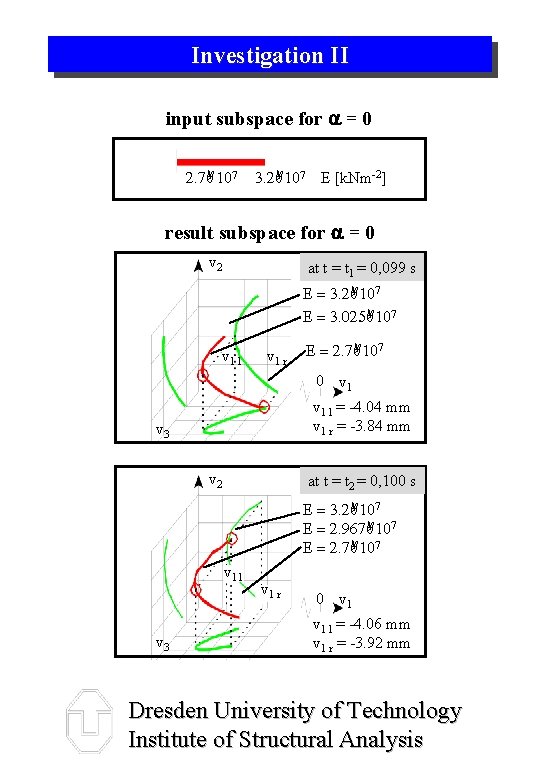
Investigation II input subspace for = 0 2. 7 A 107 3. 2 A 107 E [k. Nm-2] result subspace for = 0 v 2 at t = t 1 = 0, 099 s E = 3. 2 A 107 E = 3. 025 A 107 v 1 l v 1 r E = 2. 7 A 107 0 v 1 l = -4. 04 mm v 1 r = -3. 84 mm v 3 v 2 at t = t 2 = 0, 100 s E = 3. 2 A 107 E = 2. 967 A 107 E = 2. 7 A 107 v 1 l v 3 v 1 r 0 v 1 l = -4. 06 mm v 1 r = -3. 92 mm Dresden University of Technology Institute of Structural Analysis

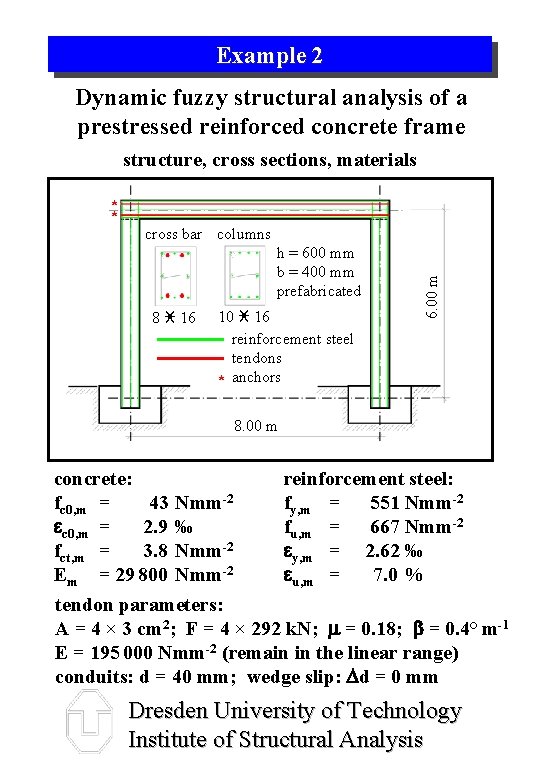
Example 2 Dynamic fuzzy structural analysis of a prestressed reinforced concrete frame structure, cross sections, materials cross bar columns h = 600 mm b = 400 mm prefabricated 8 i 16 10 i 16 reinforcement steel tendons * anchors 6. 00 m * * 8. 00 m concrete: fc 0, m = 43 ec 0, m = 2. 9 fct, m = 3. 8 Em = 29 800 Nmm-2 ‰ Nmm-2 reinforcement steel: fy, m = 551 Nmm-2 fu, m = 667 Nmm-2 ey, m = 2. 62 ‰ eu, m = 7. 0 % tendon parameters: A = 4 × 3 cm 2; F = 4 × 292 k. N; m = 0. 18; b = 0. 4° m-1 E = 195 000 Nmm-2 (remain in the linear range) conduits: d = 40 mm; wedge slip: Dd = 0 mm Dresden University of Technology Institute of Structural Analysis

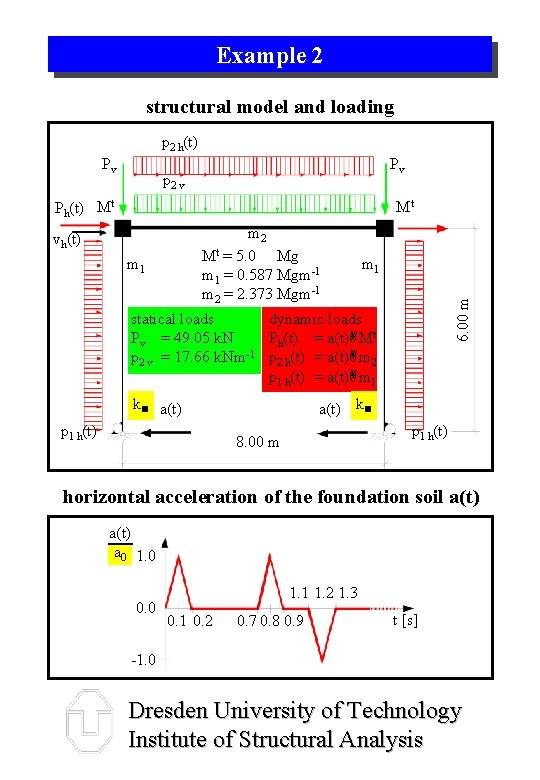
Example 2 structural model and loading p 2 h(t) Pv Pv p 2 v Ph(t) Mt Mt m 1 6. 00 m m 2 Mt = 5. 0 Mg m 1 = 0. 587 Mgm-1 m 2 = 2. 373 Mgm-1 vh(t) statical loads dynamic loads Pv = 49. 05 k. N Ph(t) = a(t)AMt p 2 v = 17. 66 k. Nm-1 p 2 h(t) = a(t)Am 2 p 1 h(t) = a(t)Am 1 k a(t) p 1 h(t) a(t) k p 1 h(t) 8. 00 m horizontal acceleration of the foundation soil a(t) a 0 1. 0 0. 0 1. 1 1. 2 1. 3 0. 1 0. 2 0. 7 0. 8 0. 9 t [s] -1. 0 Dresden University of Technology Institute of Structural Analysis

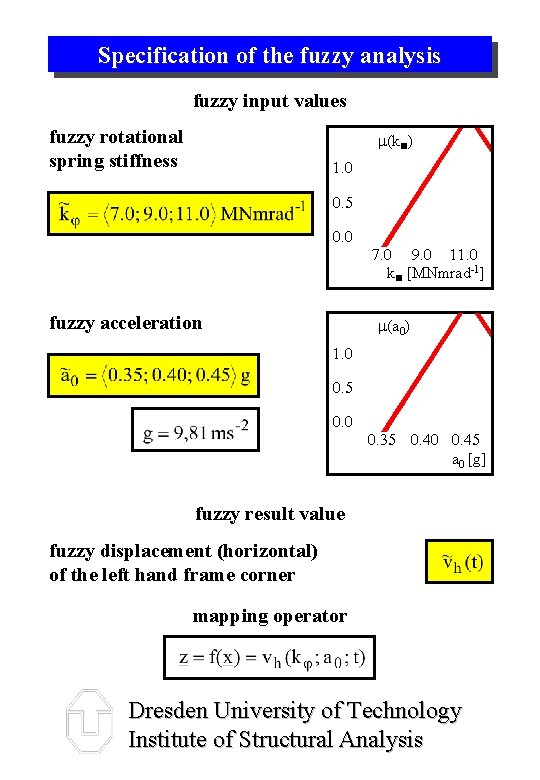
Specification of the fuzzy analysis fuzzy input values fuzzy rotational spring stiffness m(k ) 1. 0 0. 5 0. 0 fuzzy acceleration 7. 0 9. 0 11. 0 k [MNmrad-1] m(a 0) 1. 0 0. 5 0. 0 0. 35 0. 40 0. 45 a 0 [g] fuzzy result value fuzzy displacement (horizontal) of the left hand frame corner mapping operator Dresden University of Technology Institute of Structural Analysis

Deterministic fundamental solution plane structural model with imperfect straight bars and layered cross sections numerical integration of the differential equation system 1 st order in the bars interaction of internal forces incremental-iterative solution technique to consider complex loading processes consideration of all essential geometrical and physical nonlinearities large displacements and moderate rotations realistic material description of reinforced concrete including cyclic and damage effects Dresden University of Technology Institute of Structural Analysis

Numerical simulation constructing and loading process prestressing of all tendons and grouting of the conduits, no dead weight of the columns, hinged connection of the columns and the cross bar, dead weight of the cross bar transformation of the hinged joints into rigid connections (frame corners) additional translational mass at the frame corners and along the cross bar (statical loads) dynamic loads due to the time dependent uncertain horizontal acceleration a(t) dynamic analysis numerical time step integration using a modified Newmark operator, Dt = 0. 025 s Dresden University of Technology Institute of Structural Analysis

Fuzzy results horizontal displacement ~vh(t) of the left hand frame corner vh [mm] a = 0. 0 a = 1. 0 (linear analysis) 120 60 0 -60 -120 -180 0. 5 1. 0 1. 5 2. 0 2. 5 t [s] ~ largest fuzzy bending moment Mb at the right hand column base m(Mb) 1. 0 0. 0 linear 0. 0 nonlinear analysis 55. 9 81. 8 109. 0 141. 8 182. 8 222. 6 Mb [k. Nm] Dresden University of Technology Institute of Structural Analysis

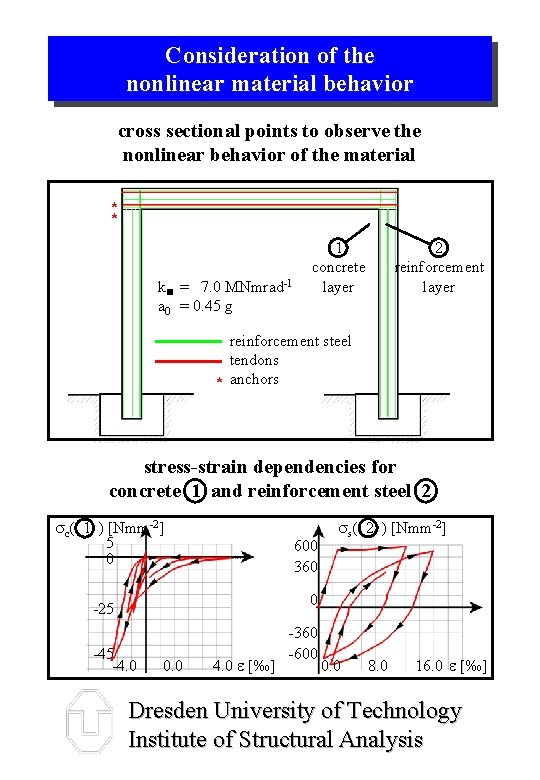
Consideration of the nonlinear material behavior cross sectional points to observe the nonlinear behavior of the material * * k = 7. 0 MNmrad-1 a 0 = 0. 45 g 1 concrete layer 2 reinforcement layer reinforcement steel tendons * anchors stress-strain dependencies for concrete 1 and reinforcement steel 2 sc( 1 ) [Nmm-2] 5 0 600 360 ss( 2 ) [Nmm-2] 0 -25 -4. 0 0. 0 4. 0 e [‰] -360 -600 0. 0 8. 0 16. 0 e [‰] Dresden University of Technology Institute of Structural Analysis

Conclusions Conditions for realistic structural analysis and safety assessment · suitably matched computational models · reliable input and model parameters, uncertainty has to be accounted for in its natural form „There is nothing so wrong with the analysis as believing the answer!“ Richard P. Feynman Dresden University of Technology Institute of Structural Analysis