Fuzzy Relations Review Fuzzy Relations Crisp Relation Definition

Fuzzy Relations Review Fuzzy Relations

Crisp Relation Definition (Product set): Let A and B be two nonempty sets, the product set or Cartesian product A B is defined as follows, A B {(a, b) | a A, b B } Extension to n sets A 1 A 2. . . An = {(a 1, . . . , an) | a 1 A 1, a 2 A 2, . . . , an An }

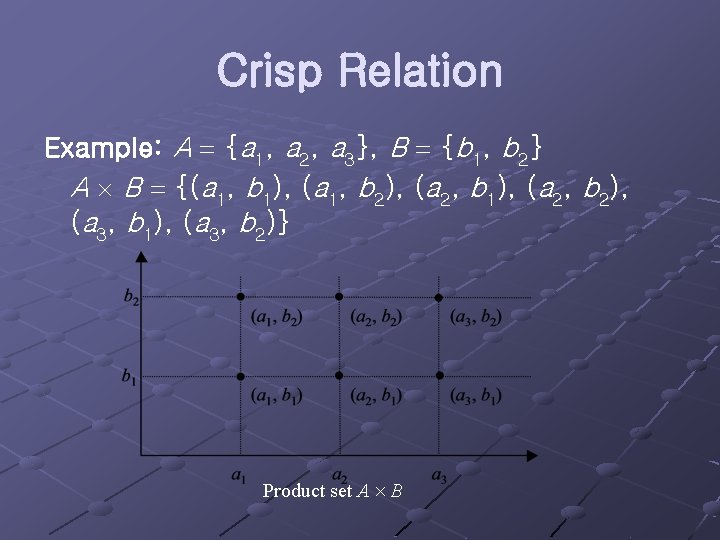
Crisp Relation Example: A {a 1, a 2, a 3}, B {b 1, b 2} A B {(a 1, b 1), (a 1, b 2), (a 2, b 1), (a 2, b 2), (a 3, b 1), (a 3, b 2)} Product set A B

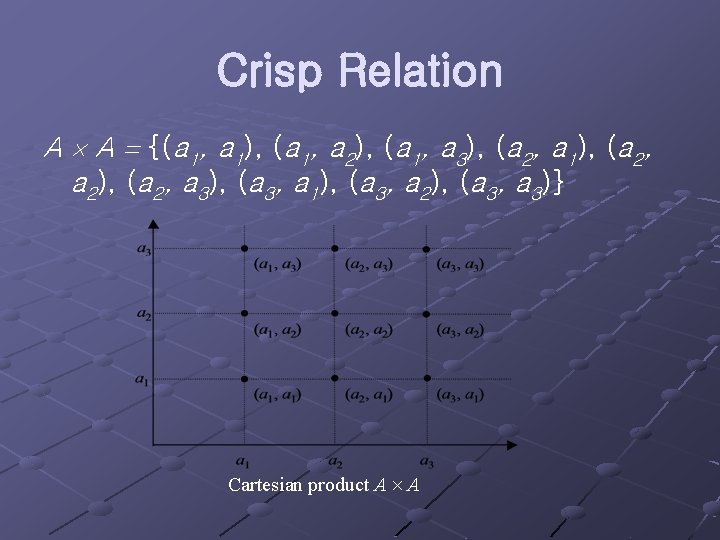
Crisp Relation A A {(a 1, a 1), (a 1, a 2), (a 1, a 3), (a 2, a 1), (a 2, a 2), (a 2, a 3), (a 3, a 1), (a 3, a 2), (a 3, a 3)} Cartesian product A A

Crisp Relation Definition n Binary Relation R = { (x, y) | x A, y B } A x B n n-ary Relation (x 1, x 2, x 3, … , xn) R , R A 1 A 2 A 3 … An

Crisp Relation Domain and Range dom(R) = { x | x A, (x, y) R for some y B } ran(R) = { y | y B, (x, y) R for some x A } A B x 1 dom(R ) R ran(R ) dom(R) , ran(R) f y 1 x 2 y 2 x 3 y 3 Mapping y f(x)

Crisp Relation Characteristics of relation (1) One-to-many x A, y 1, y 2 B (x, y 1) R, (x, y 2) R (2) Surjection (many-to-one) f(A) B or ran(R) B. y B, x A, y f(x) Thus, even if x 1 x 2, f(x 1) f(x 2) can hold. A B A y x 1 y 2 One-to-many relation (not a function) x 1 B f y x 2 Surjection

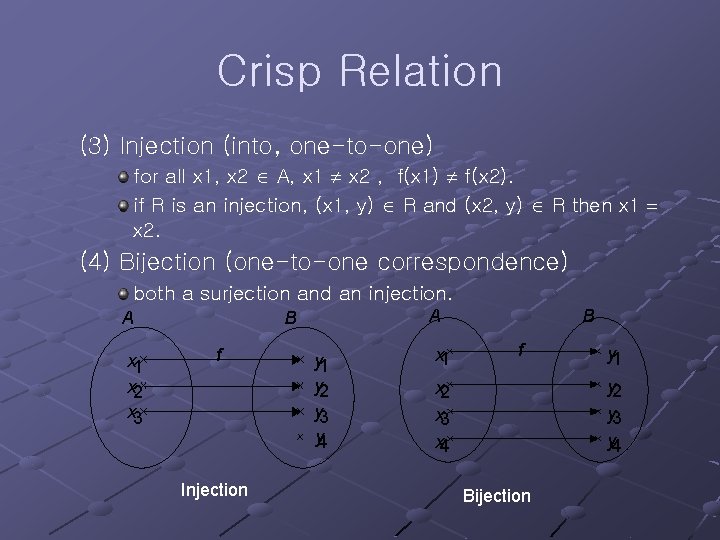
Crisp Relation (3) Injection (into, one-to-one) for all x 1, x 2 A, x 1 x 2 , f(x 1) f(x 2). if R is an injection, (x 1, y) R and (x 2, y) R then x 1 x 2. (4) Bijection (one-to-one correspondence) both a surjection and an injection. A x 1 x 2 x 3 A B f Injection y 1 y 2 y 3 y 4 x 1 B f y 1 x 2 x 3 y 2 y 3 x 4 y 4 Bijection

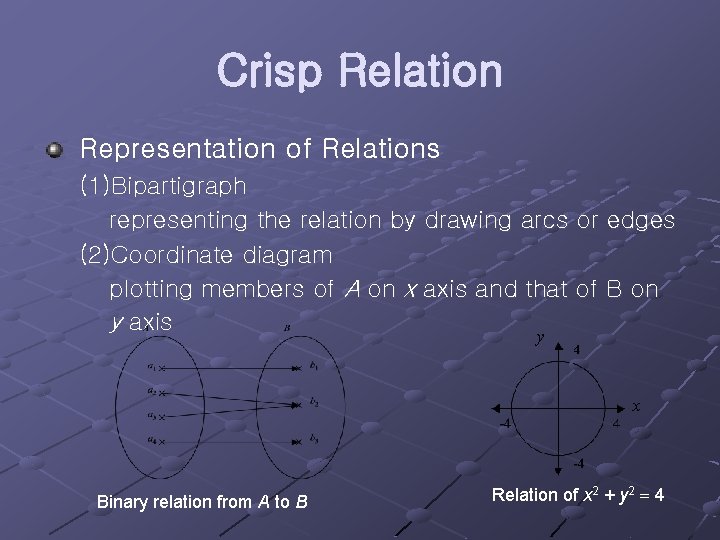
Crisp Relation Representation of Relations (1)Bipartigraph representing the relation by drawing arcs or edges (2)Coordinate diagram plotting members of A on x axis and that of B on y axis y x Binary relation from A to B Relation of x 2 + y 2 4

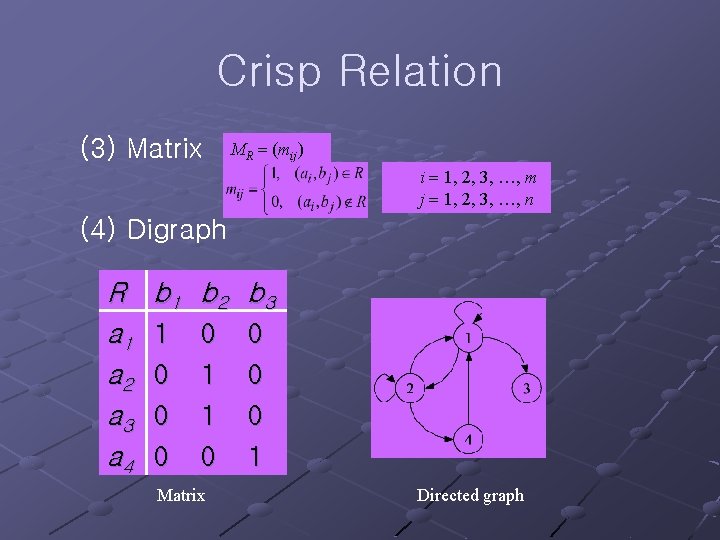
Crisp Relation (3) Matrix MR (mij) i 1, 2, 3, …, m j 1, 2, 3, …, n (4) Digraph R a 1 a 2 a 3 a 4 b 1 b 2 b 3 1 0 0 1 1 0 Matrix 0 0 0 1 Directed graph

Crisp Relation Operations on relations R, S A B (1) Union T R S If (x, y) R or (x, y) S, then (x, y) T (2) Intersection T R S If (x, y) R and (x, y) S, then (x, y) T. (3) Complement If (x, y) R, then (x, y) RC (4) Inverse R-1 {(y, x) B A | (x, y) R, x A, y B} (5) Composition T R A B, S B C , T S R A C T {(x, z) | x A, y B, z C, (x, y) R, (y, z) S}

Types of Relation on a set Reflexive relation x A (x, x) R or R(x, x) = 1, x A n n irreflexive if it is not satisfied for some x A antireflexive if it is not satisfied for all x A Symmetric relation (x, y) R (y, x) R or R(x, y) = R(y, x), x, y A n n asymmetric or nonsymmetric when for some x, y A, (x, y) R and (y, x) R. antisymmetric if for all x, y A, (x, y) R and (y, x) R

Types of Relation on a Set Transitive relation For all x, y, z A (x, y) R, (y, z) R (x, z) R 2 1 2 3 3 1 4 4 (b) R (a) R Transitive Closure

Types of Relation on a Set Equivalence relation (1) Reflexive x A (x, x) R (2) Symmetric (x, y) R (y, x) R (3) Transitive relation (x, y) R, (y, z) R (x, z) R

Types of Relation on a Set Equivalence classes a partition of A into n disjoint subsets A 1, A 2, . . . , An (a) Expression by set (b) Expression by undirected graph Partition by equivalence relation (A/R) {A 1, A 2} {{a, b, c}, {d, e}}

Types of Relation on a Set Compatibility relation (tolerance relation) (1) Reflexive relation x A (x, x) R (a) Expression by set (2) Symmetric relation (x, y) R (y, x) R (b) Expression by undirected graph Partition by compatibility relation

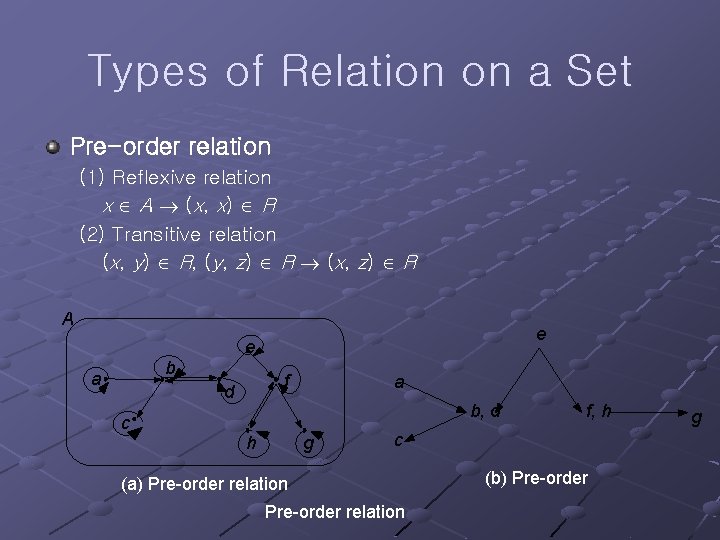
Types of Relation on a Set Pre-order relation (1) Reflexive relation x A (x, x) R (2) Transitive relation (x, y) R, (y, z) R (x, z) R A e e b a f d c a b, d h g f, h c (a) Pre-order relation (b) Pre-order g

Types of Relation on a Set Order relation n (1) Reflexive relation x A (x, x) R (2) Antisymmetric relation (x, y) R (y, x) R (3) Transitive relation (x, y) R, (y, z) R (x, z) R strict order relation (1’) Antireflexive relation x A (x, x) R n total order or linear order relation (4) x, y A, (x, y) R or (y, x) R

Types of Relations on a Set Comparison of relations Property Relation Equivalence Compatibility Pre-order Order Strict order Reflexive Anti reflexive Symmetric Anti symmetric Transitive

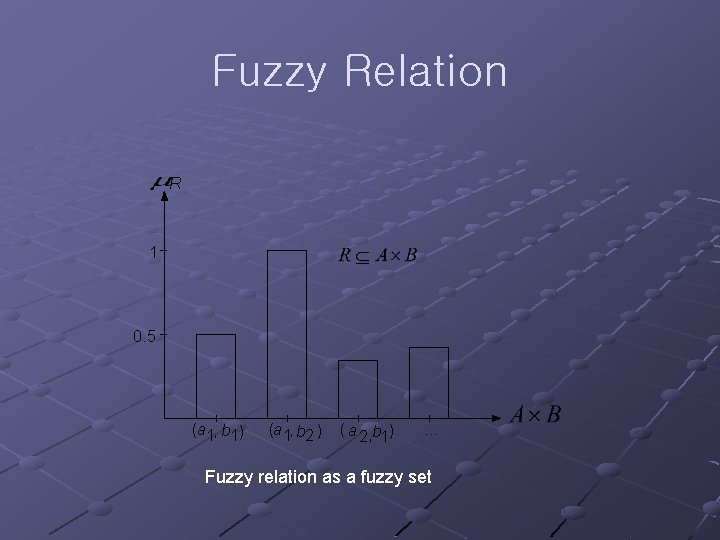
Fuzzy Relation Definition of fuzzy relation n Crisp relation membership function R(x, y) R : A B {0, 1} R (x, y) = n 1 iff (x, y) R 0 iff (x, y) R Fuzzy relation R : A B [0, 1] R = {((x, y), R(x, y))| R(x, y) 0 , x A, y B}

Fuzzy Relation R 1 0. 5 (a 1, b 1 ) (a 1, b 2 ) ( a 2, b 1) . . . Fuzzy relation as a fuzzy set

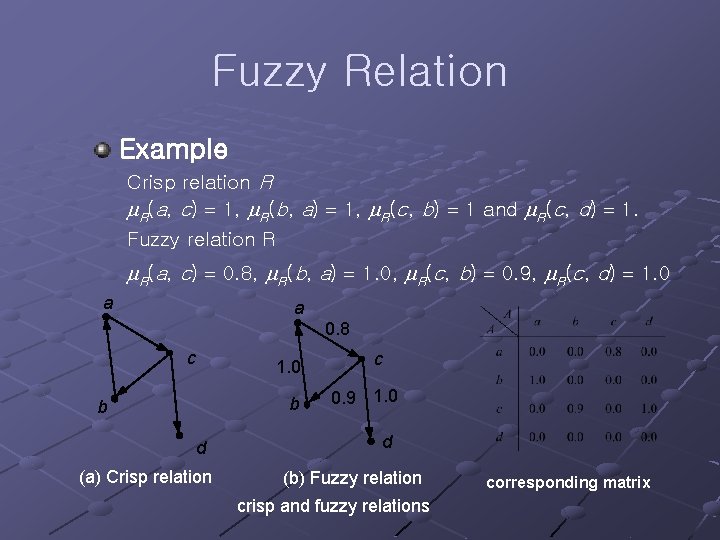
Fuzzy Relation Example Crisp relation R R(a, c) 1, R(b, a) 1, R(c, b) 1 and R(c, d) 1. Fuzzy relation R R(a, c) 0. 8, R(b, a) 1. 0, R(c, b) 0. 9, R(c, d) 1. 0 a a 0. 8 c 1. 0 b b d (a) Crisp relation c 0. 9 1. 0 d (b) Fuzzy relation crisp and fuzzy relations corresponding matrix

Fuzzy Relation Operation of Fuzzy Relation 1) Union relation (x, y) A B R S (x, y) Max [ R (x, y), S (x, y)] R (x, y) S (x, y) 2) Intersection relation R S (x) = Min [ R (x, y), S (x, y)] = R (x, y) S (x, y) 3) Complement relation (x, y) A B R (x, y) 1 - R (x, y) 4) Inverse relation For all (x, y) A B, R-1 (y, x) R (x, y)

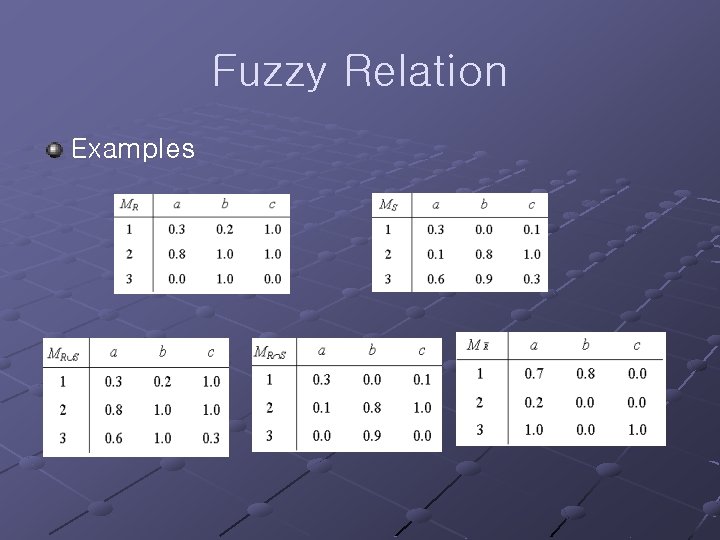
Fuzzy Relation Examples

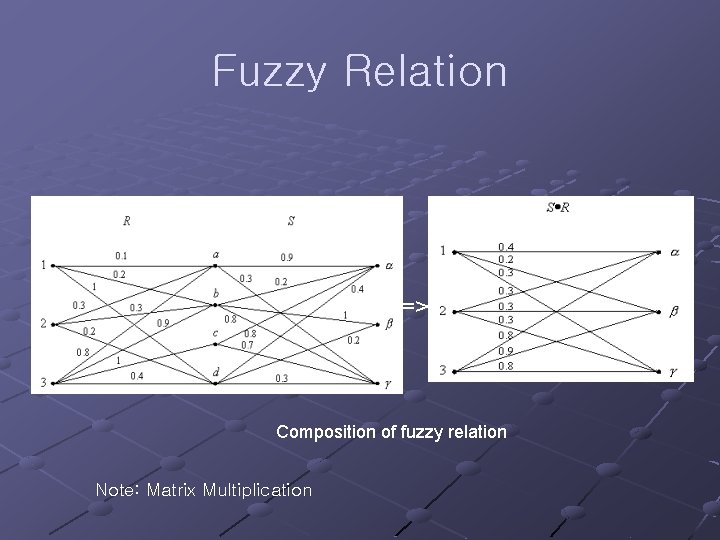
Fuzzy Relation (Standard) Composition n For (x, y) A B, (y, z) B C, R S (x, z) = Max [Min ( R (x, y), S (y, z))] y = [ R (x, y) S (y, z)] y MR S MR MS n Example =>

Fuzzy Relation => Composition of fuzzy relation Note: Matrix Multiplication

Fuzzy Relation -cut of fuzzy relation R = {(x, y) | R(x, y) , x A, y B} : a crisp relation. Example

Fuzzy Relation Decomposition of Fuzzy Relation n Example

Fuzzy Relation Projection n Example

Fuzzy Relation n Projection in n dimension n Cylindrical extension C (R ) ( a , b , c ) R ( a , b ) a A, b B , c C n Example

Types of Fuzzy Relations Reflexive n n n Irreflexive Antireflexive Epsilon Reflexive Symmetric n n Asymmetric Antisymmetric

Types of Fuzzy Relations Transitive (max-min transitive) n n Non-transitive: For some (x, z), the above do not satisfy. Antitransitive: Example: X = Set of cities, R=“very far” Reflexive, symmetric, non-transitive

Types of Fuzzy Relations Transitive Closure n n n Crisp: Transitive relation that contains R(X, X) with fewest possible members Fuzzy: Transitive relation that contains R(X, X) with smallest possible membership Algorithm:

Types of Fuzzy Relations Fuzzy Equivalence or Similarity Relation n Reflexive, symmetric, and transitive Decomposition: n Partition Tree n

Types of Fuzzy Relations Fuzzy Compatibility or Tolerance Relation n n Reflexive and symmetric Maximal compatibility class and complete cover Compatibility class Maximal compatibility class: largest compatibility class Complete cover: Set of maximal compatibility classes n n n Maximal alpha-compatibility class Complete alpha-covers Note: Relation from distance metrics forms tolerance relation in clustering.

Fuzzy Morphism Homomorphism n n Preserve relations by a function Example: Log function preserves the order of real data.

Other Compositions Sup-I composition INF-omega i composition n Degree of Implication i=min: a < b then 1, otherwise b. INF-omega i composition

Extension of fuzzy set Extension by relation n Extension of fuzzy set x A, y B y f(x) or x f -1(y) for y B if f -1(y) Example: A {(a 1, 0. 4), (a 2, 0. 5), (a 3, 0. 9), (a 4, 0. 6)}, B {b 1, b 2, b 3} f -1(b 1) {(a 1, 0. 4), (a 3, 0. 9)}, Max [0. 4, 0. 9] 0. 9 B' (b 1) 0. 9 f -1(b 2) {(a 2, 0. 5), (a 4, 0. 6)}, Max [0. 5, 0. 6] 0. 6 B' (b 2) 0. 6 f -1(b 3) {(a 4, 0. 6)} B' (b 3) 0. 6 B' {(b 1, 0. 9), (b 2, 0. 6), (b 3, 0. 6)}

Extension of Fuzzy Set Extension principle n Extension principle A 1 A 2 . . . Ar ( x 1 x 2 . . . xr ) Min [ A 1 (x 1), . . . , Ar(xr) ] f(x 1, x 2, . . . , xr) : X Y

Extension of Fuzzy Set Example:

Extension of fuzzy set Extension by fuzzy relation For x A, y B, and B B B' (y) Max [Min ( A (x), R (x, y))] x f -1(y) n Example For b 1 Min [ A (a 1), R (a 1, b 1)] Min [0. 4, 0. 8] 0. 4 Min [ A (a 3), R (a 3, b 1)] Min [0. 9, 0. 3] 0. 3 Max [0. 4, 0. 3] 0. 4 B' (b 1) 0. 4 For b 2, Min [ A (a 2), R (a 2, b 2)] Min [0. 5, 0. 2] 0. 2 Min [ A (a 4), R (a 4, b 2)] Min [0. 6, 0. 7] 0. 6 Max [0. 2, 0. 6] 0. 6 B' (b 2) 0. 6 For b 3, Max Min [ A (a 4), R (a 4, b 3)] Max Min [0. 6, 0. 4] 0. 4 B' (b 3) 0. 4 B' {(b 1, 0. 4), (b 2, 0. 6), (b 3, 0. 4)}

Extension of Fuzzy Set n Example A {(a 1, 0. 8), (a 2, 0. 3)} B {b 1 , b 2 , b 3 } C {c 1 , c 2 , c 3 } B' {(b 1, 0. 3), (b 2, 0. 8), (b 3, 0)} C' {(c 1, 0. 3), (c 2, 0. 3), (c 3, 0. 8)}

Extension of fuzzy set Fuzzy distance between fuzzy sets n Pseudo-metric distance (1) d(x, x) 0, x X (2) d(x 1, x 2) d(x 2, x 1), x 1, x 2 X (3) d(x 1, x 3) d(x 1, x 2) d(x 2, x 3), x 1, x 2, x 3 X + (4) if d(x 1, x 2)=0, then x 1 = x 2 metric distance n Distance between fuzzy sets , d(A, B)( ) Max d(a, b) [Min ( A(a), B(b))]

Extension of Fuzzy Set Example A {(1, 0. 5), (2, 1), (3, 0. 3)} B {(2, 0. 4), (3, 0. 4), (4, 1)}