Fuzzy Logic 1 Intelligent System Course Apples oranges










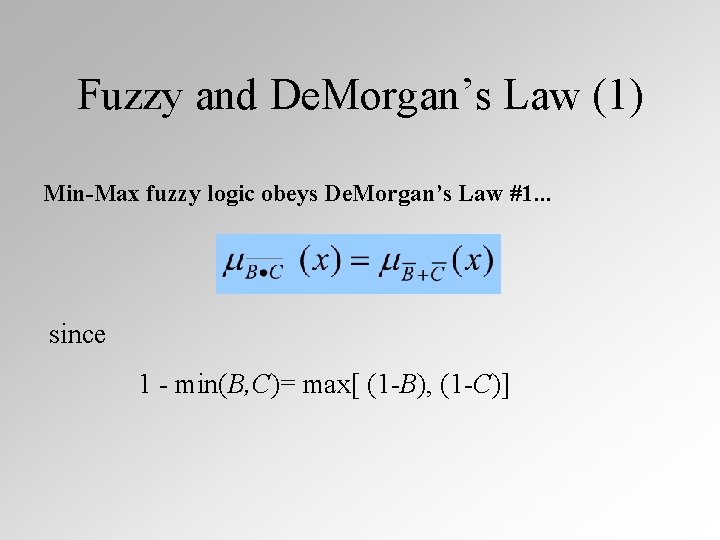
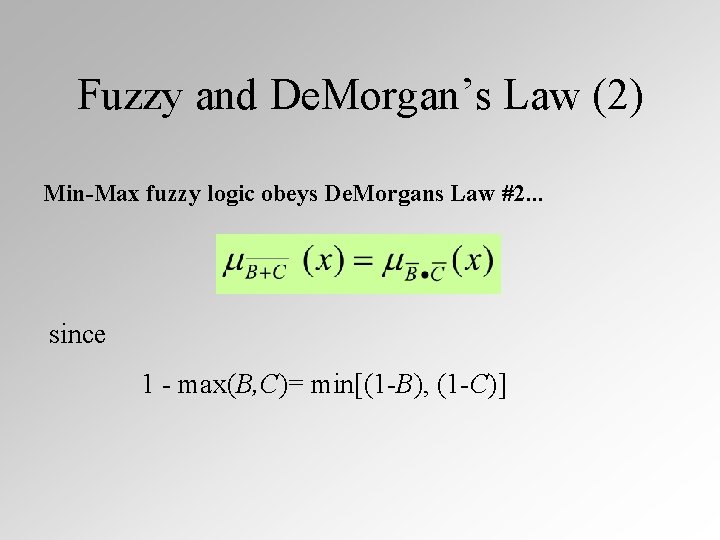
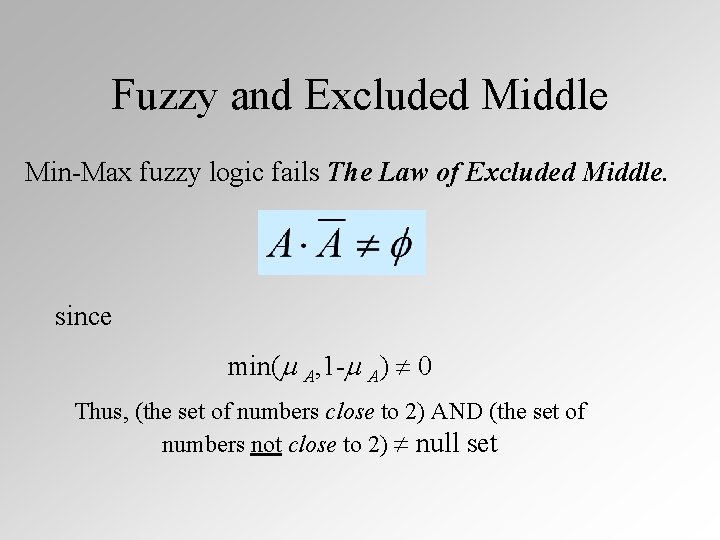


- Slides: 23

Fuzzy Logic (1) Intelligent System Course

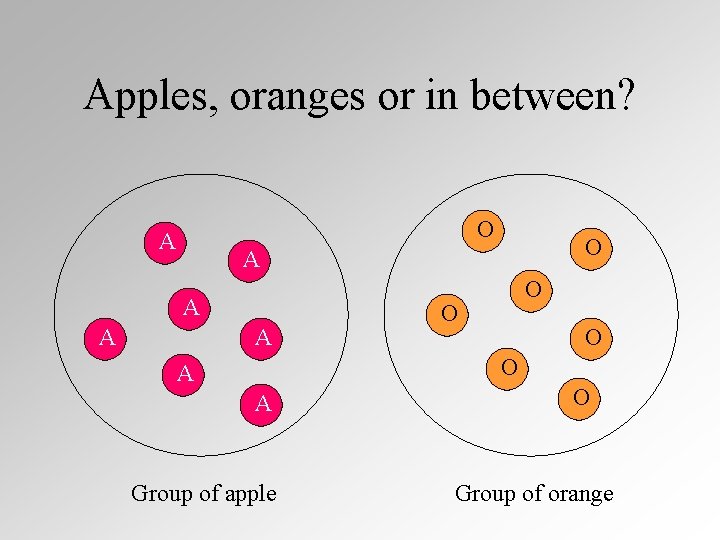
Apples, oranges or in between? O A A A A O O A A Group of apple O Group of orange

Lotfi Zadeh

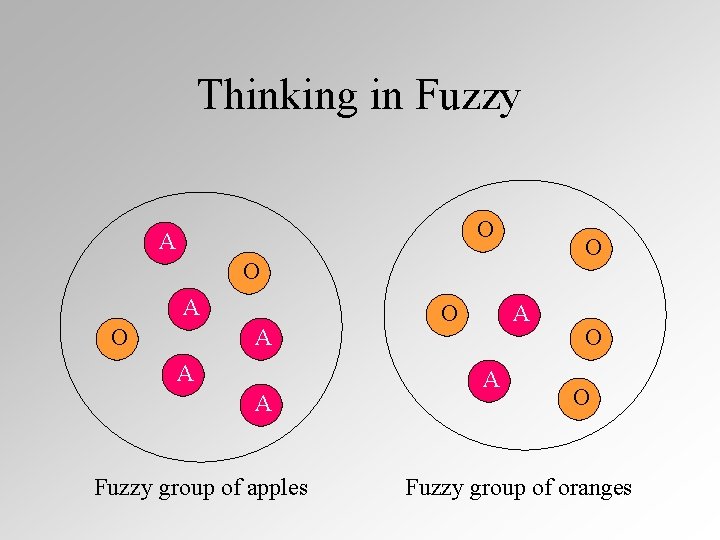
Thinking in Fuzzy O A O A A A Fuzzy group of apples O A A O O Fuzzy group of oranges

Crisp vs Fuzzy • Crisp sets handle only 0 s and 1 s • Fuzzy sets handle all values between 0 and 1 Crisp No Yes No Fuzzy Slightly Mostly Yes

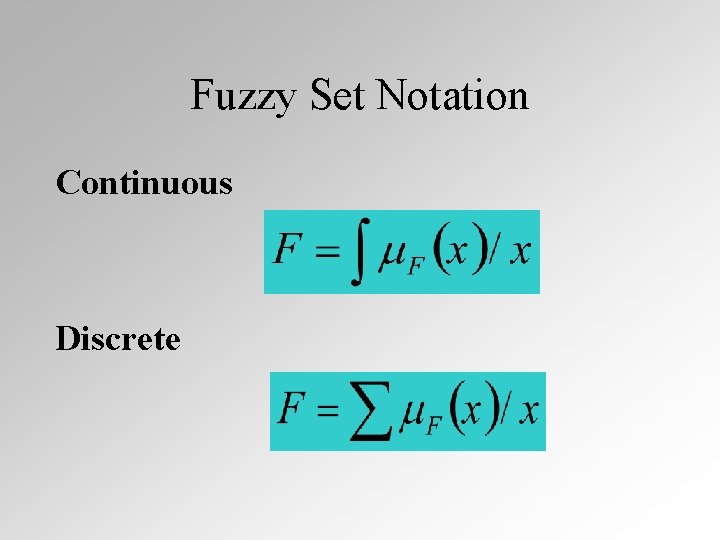
Fuzzy Set Notation Continuous Discrete

Continuous Fuzzy Membership Function • The set, B, of numbers near to two is B(x) 0 1 2 3 x

Discrete Fuzzy Membership Function The set, B, of numbers near to two is B(x) 0 1 2 3 x

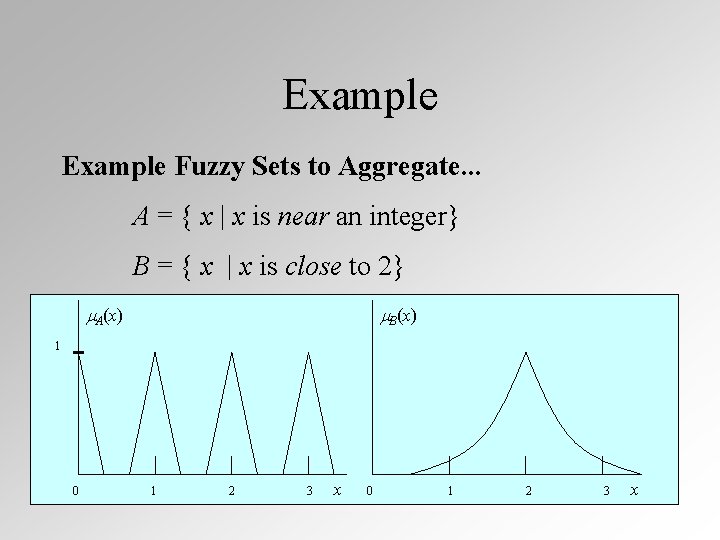
Example Fuzzy Sets to Aggregate. . . A = { x | x is near an integer} B = { x | x is close to 2} B(x) A(x) 1 0 1 2 3 x

Fuzzy Union • Fuzzy Union (logic “or”) 4 Meets crisp boundary conditions 4 Commutative 4 Associative 4 Idempotent

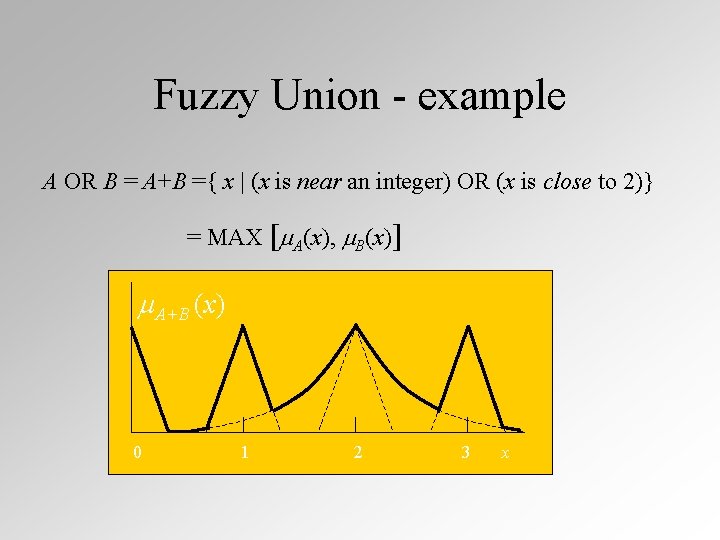
Fuzzy Union - example A OR B = A+B ={ x | (x is near an integer) OR (x is close to 2)} = MAX [ A(x), B(x)] A+B (x) 0 1 2 3 x

Fuzzy Intersection • Fuzzy Intersection (logic “and”) 4 Meets crisp boundary conditions 4 Commutative 4 Associative 4 Idempotent

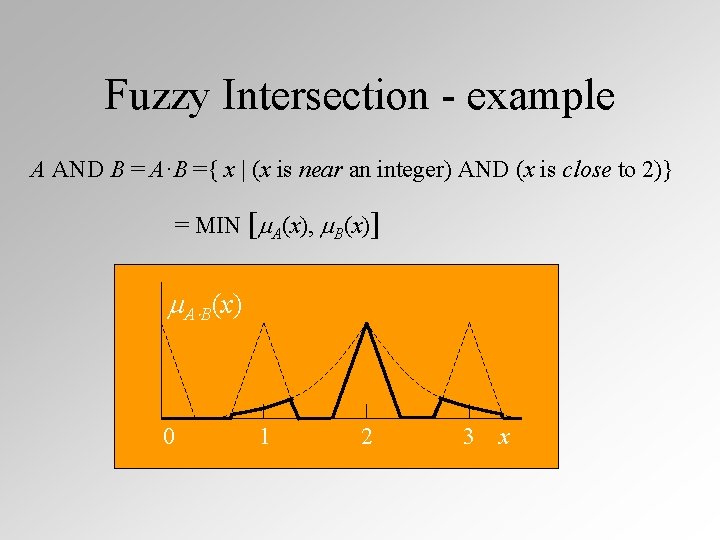
Fuzzy Intersection - example A AND B = A·B ={ x | (x is near an integer) AND (x is close to 2)} = MIN [ A(x), B(x)] A B(x) 0 1 2 3 x

Fuzzy Complement The complement of a fuzzy set has a membership function. . . 4 Meets crisp boundary conditions 4 Two Negatives Should Make a Positive 4 Law of Excluded Middle: NO! 4 Law of Contradiction: NO!

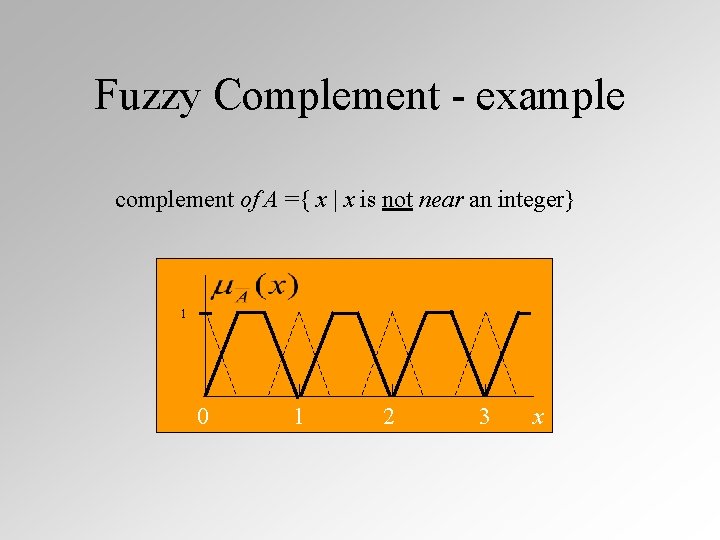
Fuzzy Complement - example complement of A ={ x | x is not near an integer} 1 0 1 2 3 x

Fuzzy Associativity (1) Min-Max fuzzy logic has intersection distributive over union. . . since min[ A, max(B, C) ]=min[ max(A, B), max(A, C) ]

Fuzzy Associativity (2) Min-Max fuzzy logic has union distributive over intersection. . . since max[ A, min(B, C) ]= max[ min(A, B), min(A, C) ]
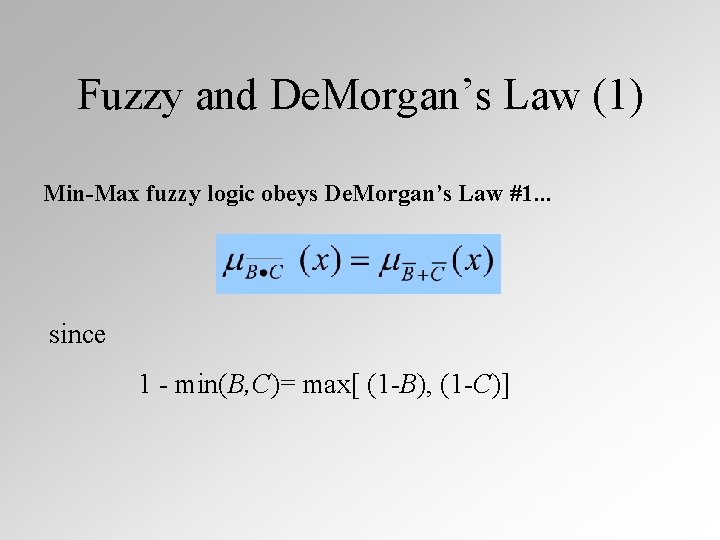
Fuzzy and De. Morgan’s Law (1) Min-Max fuzzy logic obeys De. Morgan’s Law #1. . . since 1 - min(B, C)= max[ (1 -B), (1 -C)]
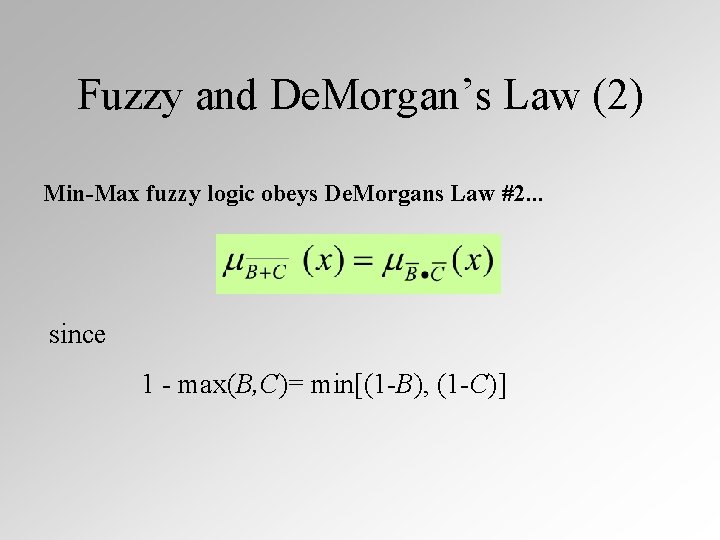
Fuzzy and De. Morgan’s Law (2) Min-Max fuzzy logic obeys De. Morgans Law #2. . . since 1 - max(B, C)= min[(1 -B), (1 -C)]
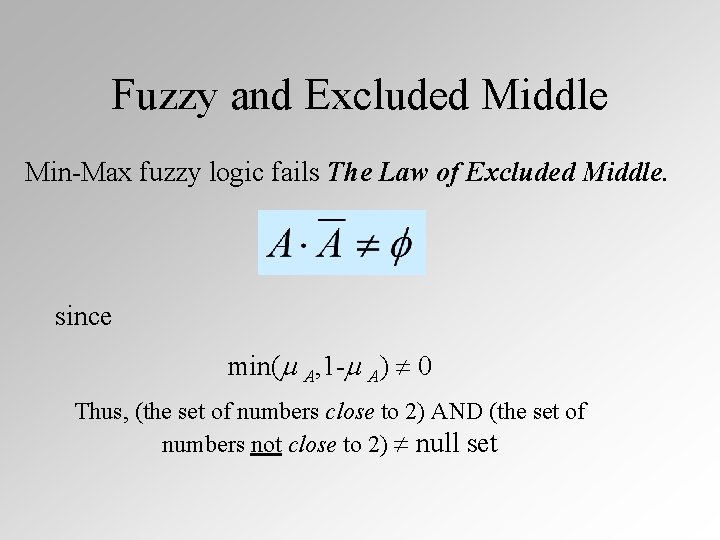
Fuzzy and Excluded Middle Min-Max fuzzy logic fails The Law of Excluded Middle. since min( A, 1 - A) 0 Thus, (the set of numbers close to 2) AND (the set of numbers not close to 2) null set

Fuzzy and the Law of Contradiction Min-Max fuzzy logic fails the The Law of Contradiction. since max( A, 1 - A) 1 Thus, (the set of numbers close to 2) OR (the set of numbers not close to 2) universal set

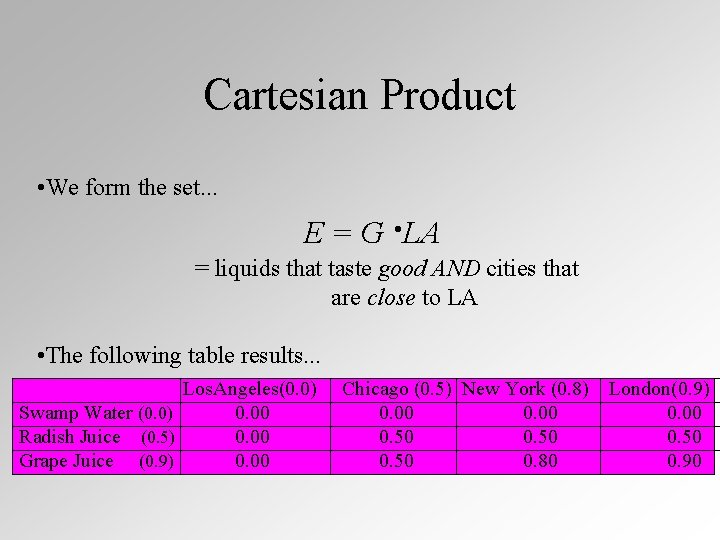
Cartesian Product • The intersection and union operations can also be used to assign memberships on the Cartesian product of two sets. • Consider, as an example, the fuzzy membership of a set, G, of liquids that taste good and the set, LA, of cities close to Los Angeles

Cartesian Product • We form the set. . . E = G ·LA = liquids that taste good AND cities that are close to LA • The following table results. . . Los. Angeles(0. 0) Swamp Water (0. 0) 0. 00 Radish Juice (0. 5) 0. 00 Grape Juice (0. 9) 0. 00 Chicago (0. 5) New York (0. 8) 0. 00 0. 50 0. 80 London(0. 9) 0. 00 0. 50 0. 90