FUZZY INFERENCE SYSTEMS MATERI KULIAH PERTEMUAN 11 Logika

FUZZY INFERENCE SYSTEMS MATERI KULIAH (PERTEMUAN 11) Logika Fuzzy Jurusan Teknik Informatika Samuel Wibisono 1

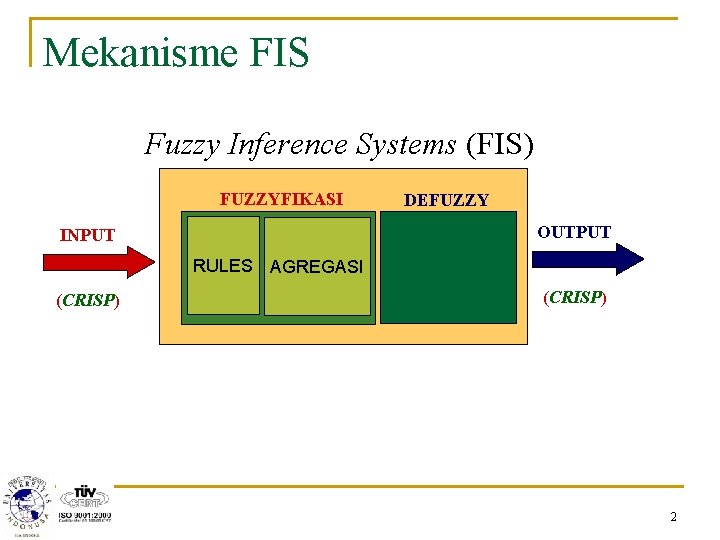
Mekanisme FIS Fuzzy Inference Systems (FIS) FUZZYFIKASI DEFUZZY OUTPUT INPUT RULES AGREGASI (CRISP) 2

Pokok Bahasan n n Metode Mamdani Metode Sugeno 3

Metode Mamdani n n n Metode Mamdani sering juga dikenal dengan nama Metode Max-Min. Menggunakan MIN pada fungsi implikasi, dan MAX pada komposisi antar fungsi implikasi. Diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. 4

Langkah-langkah FIS: MAMDANI n n n Tentukan variabel-variabel & himpunan fuzzy; Tentukan fungsi keanggotaan; Lakukan implementasi fungsi implikasi; Lakukan komposisi/agregasi aturan; Lakukan proses penegasan (defuzzy) Model Inferensi 5

FUNGSI IMPLIKASI n Bentuk umum: IF (x 1 is A 1) · (x 2 is A 2) ·. . . · (x. N is AN) THEN y is B dengan · adalah operator (misal: OR atau AND), x 1, x 2, …, x. N adalah variabel-variabel input, y adalah variabel output, A 1, A 2, …, AN, B, adalah himpunan-himpunan fuzzy. 6

Ada 2 fungsi implikasi: n n Min (minimum) Dot (product) 7

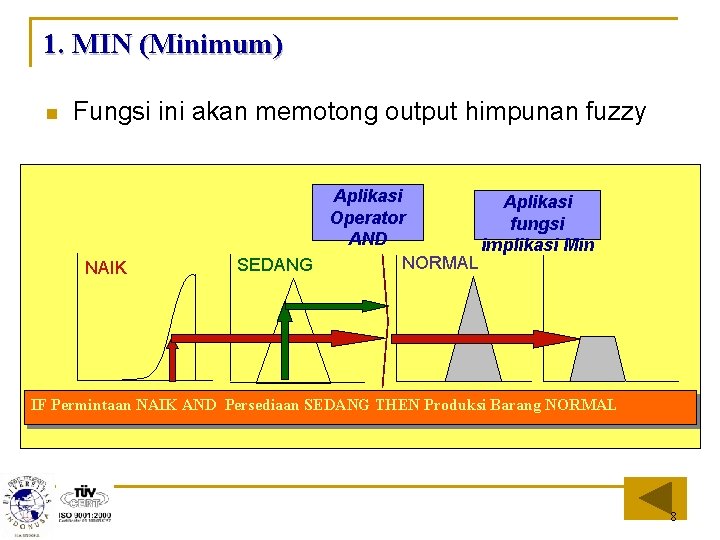
1. MIN (Minimum) n Fungsi ini akan memotong output himpunan fuzzy NAIK Aplikasi Operator fungsi AND implikasi Min NORMAL SEDANG IF Permintaan NAIK AND Persediaan SEDANG THEN Produksi Barang NORMAL 8

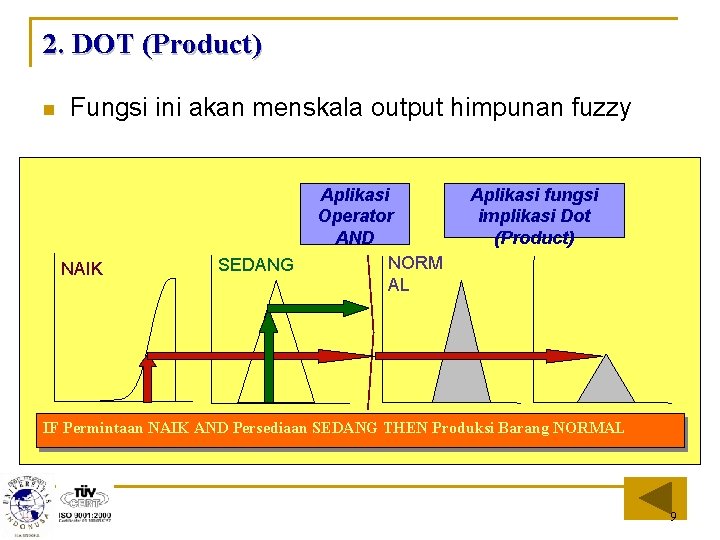
2. DOT (Product) n Fungsi ini akan menskala output himpunan fuzzy NAIK SEDANG Aplikasi Operator AND NORM AL Aplikasi fungsi implikasi Dot (Product) IF Permintaan NAIK AND Persediaan SEDANG THEN Produksi Barang NORMAL 9

Metode Komposisi n n n Metode Max Metode Additive Metode Probabilistik OR (PROBOR) 10

1. Metode MAX (Maximum) n n Solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikannya ke output dengan menggunakan operator OR (union). Secara umum dapat dituliskan: msf[xi] ¬ max(msf[xi], mkf[xi]) dengan: msf[xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i; mkf[xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i; n Apabila digunakan fungsi implikasi MIN, maka metode komposisi ini sering disebut dengan nama MAX-MIN atau MINMAX atau MAMDANI. 11

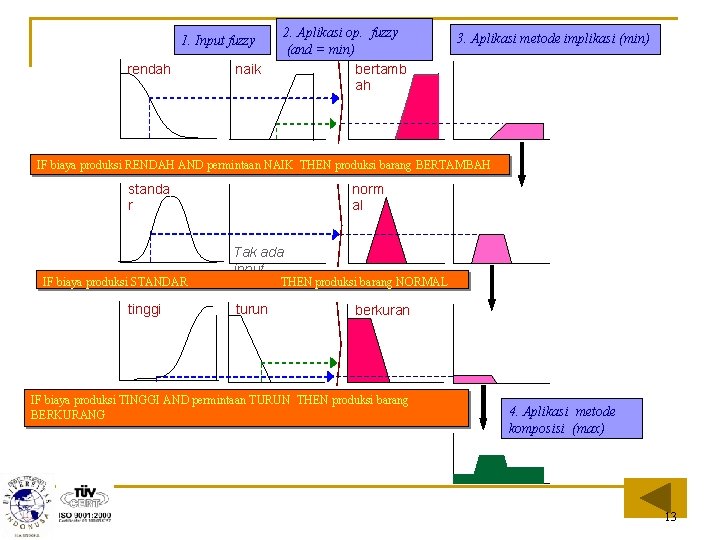
Contoh: Misalkan ada 3 aturan (proposisi) sebagai berikut: [R 1] IF Biaya Produksi RENDAH And Permintaan NAIK THEN Produksi Barang BERTAMBAH; [R 2] IF Biaya Produksi STANDAR THEN Produksi Barang NORMAL; IF Biaya Produksi TINGGI And Permintaan TURUN THEN Produksi Barang BERKURANG; [R 3] 12

1. Input fuzzy rendah naik 2. Aplikasi op. fuzzy (and = min) bertamb ah 3. Aplikasi metode implikasi (min) IF biaya produksi RENDAH AND permintaan NAIK THEN produksi barang BERTAMBAH standa r IF biaya produksi STANDAR tinggi norm al Tak ada input THEN produksi barang NORMAL turun berkuran g IF biaya produksi TINGGI AND permintaan TURUN THEN produksi barang BERKURANG 4. Aplikasi metode komposisi (max) 13

2. Metode ADDITIVE n n Solusi himpunan fuzzy diperoleh dengan cara melakukan bounded-sum terhadap semua output daerah fuzzy. Secara umum dituliskan: msf[xi] ¬ min(1, msf[xi]+ mkf[xi]) dengan: msf[xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i; mkf[xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i 14

3. Metode PROBABILISTIK OR (PROBOR) n n Solusi himpunan fuzzy diperoleh dengan cara melakukan product terhadap semua output daerah fuzzy. Secara umum dituliskan: msf[xi] ¬ (msf[xi]+ mkf[xi]) - (msf[xi] * mkf[xi]) dengan: msf[xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i; mkf[xi] = nilai keanggotaan konsekuen fuzzy aturan ke-i; 15

PENEGASAN (DEFUZZY) n n n Input dari proses defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari komposisi aturan-aturan fuzzy. Sedangkan output yang dihasilkan merupakan suatu bilangan pada domain himpunan fuzzy tersebut. Jika diberikan suatu himpunan fuzzy dalam range tertentu, maka harus dapat diambil suatu nilai crsip tertentu sebagai output 16

17

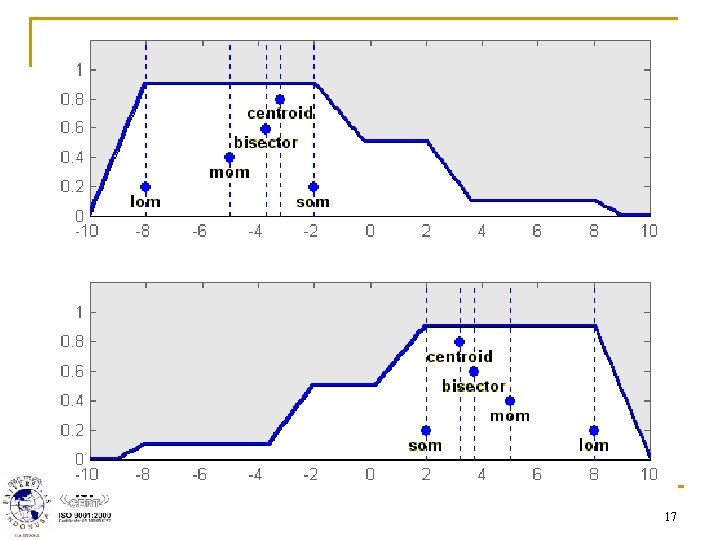
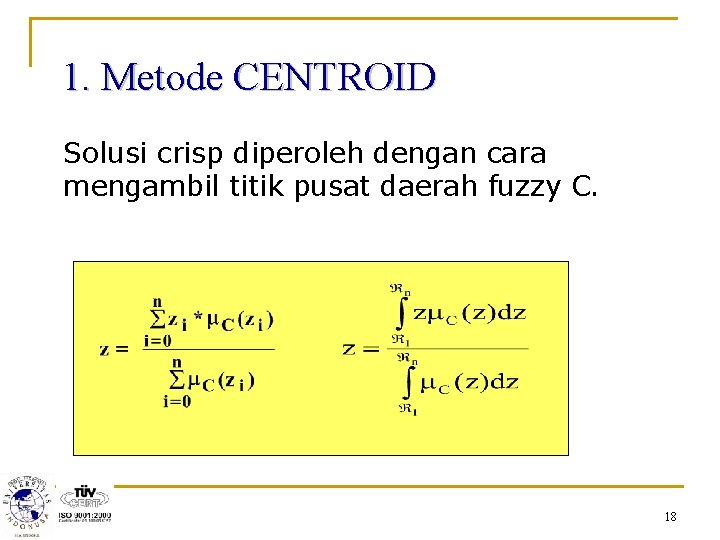
1. Metode CENTROID Solusi crisp diperoleh dengan cara mengambil titik pusat daerah fuzzy C. 18

2. Metode BISEKTOR Solusi crisp diperoleh dengan cara mengambil nilai pada domain fuzzy yang memiliki nilai keanggotaan separo dari jumlah total nilai keanggotaan pada daerah fuzzy C. 19

3. Metode MEAN OF MAXIMUM (MOM) Solusi crisp diperoleh dengan cara mengambil nilai rata-rata domain pada himpunan C yang memiliki nilai keanggotaan maksimum. z = mean{zi | m. C(zi) = maksimum m. C} 20

4. Metode SMALLEST OF MAXIMUM (SOM) Solusi crisp diperoleh dengan cara mengambil nilai terkecil dari domain pada himpunan C yang memiliki nilai keanggotaan maksimum. z = min{abs(zi) | m. C(zi) = maksimum m. C} 21

5. Metode LARGEST OF MAXIMUM (LOM) Solusi crisp diperoleh dengan cara mengambil nilai terbesar dari domain pada himpunan C yang memiliki nilai keanggotaan maksimum. z = max{abs(zi) | m. C(zi) = maksimum m. C} 22

MIN m[x] A 1 1 0 m[x] 1 m[y] 1 Var-1 A 3 0 B 3 C 3 m[z] 1 C 3 0 Var-2 m[z] C 1 1 m[z] 1 Var-3 C 2 0 Var-3 m[z] 1 C 2 0 Var-1 0 Var-3 0 MAX m[z] 1 0 23

CONTOH … n Suatu perusahaan soft drink akan memproduksi minuman jenis X. n Pada 3 bulan terakhir biaya produksi untuk minuman jenis tersebut rata-rata sekitar Rp 500, - per kemasan, dan maksimum mencapai Rp 1000, - per kemasan. n Banyaknya permintaan per hari rata-rata mencapai 30000 kemasan dan maksimum hingga mencapai 60000 kemasan. n Sampai saat ini, perusahaan baru mampu memproduksi barang maksimum 100000 kemasan per hari. 24

Apabila proses produksi perusahaan tersebut menggunakan 3 aturan fuzzy sbb: [R 1] IF Biaya Produksi RENDAH And Permintaan NAIK THEN Produksi Barang BERTAMBAH; [R 2] IF Biaya Produksi sesuai STANDAR THEN Produksi Barang NORMAL; [R 3] IF Biaya Produksi TINGGI And Permintaan TURUN THEN Produksi Barang BERKURANG; Berapa jumlah minuman jenis X yang harus diproduksi, jika biaya untuk memproduksi jenis minuman tersebut diperkirakan sejumlah Rp 800 per kemasan, dan permintaannya diperkirakan mencapai 25000 kemasan per hari. 25

1. Membuat himpunan dan input fuzzy Ada 3 variabel fuzzy yang akan dimodelkan, yaitu: n Biaya produksi; terdiri-atas 3 himpunan fuzzy, yaitu: RENDAH, STANDAR, dan TINGGI. n Permintaan barang; terdiri-atas 3 himpunan fuzzy, yaitu: TURUN, BIASA, dan NAIK. n Produksi barang; terdiri-atas 3 himpunan fuzzy, yaitu: BERKURANG, NORMAL, dan BERTAMBAH. 26

A. Variabel Biaya Produksi RENDAH m[x] STANDAR TINGGI 1 0, 68 0, 32 0 0 250 500 750 800 biaya produksi (Rp) 1000 27

q Jika biaya produksi sebesar Rp 800, - maka nilai keanggotaan fuzzy pada tiap-tiap himpunan adalah: q q Himpunan fuzzy RENDAH, m. BPRendah[800]= 0, 0 Himpunan fuzzy STANDAR, m. BPStandar[800]=0, 32 diperoleh dari: p(800; 500, 500) = S(800; 500, 750, 1000) = 2[(1000 -800)/(1000 -500)]2 = 0, 32 q Himpunan fuzzy TINGGI, m. BPTinggi[800]=0, 68 diperoleh dari: S(800; 500, 750, 1000) = 1 – 2[(1000 -800)/(1000 -500)]2 = 0, 68 28

B. Variabel Permintaan TURUN BIASA NAIK 1 m[x] 0, 25 0 0 10 25 30 35 50 60 permintaan (x 1000 kemasan per hari) 29

q Jika permintaan sebanyak 25000 kemasan per hari, maka nilai keanggotaan fuzzy pada tiap-tiap himpunan adalah: q q q Himpunan fuzzy TURUN, m. Pmt. Turun[25]=0, 25 diperoleh dari: = (30 -25)/(30 -10) = 5/20 = 0, 25 Himpunan fuzzy BIASA, m. Pmt. Biasa[25]=0 Himpunan fuzzy NAIK, m. Pmt. Naik[25]=0 30

C. Variabel Produksi Barang BERKURANG NORMAL BERTAMBAH 1 Derajat keanggotaan m[x] 0 0 10 30 50 70 90 100 produksi barang (x 1000 kemasan per hari) 31

Nilai keanggotaan fuzzy pada tiap-tiap himpunan dirumuskan: Himpunan fuzzy BERKURANG: Himpunan fuzzy NORMAL: Himpunan fuzzy BERTAMBAH: 32

2. Aplikasi operator fuzzy A. Aturan ke-1: [R 1] IF Biaya Produksi RENDAH And Permintaan NAIK THEN Produksi Barang BERTAMBAH; Operator yang digunakan adalah AND, sehingga: a 1 = m. Predikat. R 1 = min(m. BPRendah[800], m. Pmt. Naik[25]) = min(0; 0) =0 33

B. Aturan ke-2: [R 2] IF Biaya Produksi STANDAR THEN Produksi Barang NORMAL; Tidak menggunakan operator, sehingga: a 2 = m. Predikat. R 2 = m. BPStandar[800] = 0, 32 34

C. Aturan ke-3: [R 3] IF Biaya Produksi TINGGI And Permintaan TURUN THEN Produksi Barang BERKURANG; Operator a 3 = = yang digunakan adalah AND, sehingga: m. Predikat. R 3 min(m. BPTinggi[800], m. Pmt. Turun[25]) min(0, 68; 0, 25) 0, 25 35

3. Aplikasi fungsi implikasi A. Aturan ke-1: Tidak ada daerah hasil implikasi (m. KFR 1 = 0). 36

B. Aturan ke-2: Pada saat m. PBNormal[z]= 0, 32 nilai z dapat ditentukan sbb: atau 0, 32 Û 0, 05 z Û z = (z-30)/20 = 1, 82 = 36, 4 0, 32 Û 0, 05 z Û z = (70 -z)/20 = 3, 18 = 63, 6 Sehingga: 37

C. Aturan ke-3: Pada saat m. PBBerkurang[z]= 0, 25 nilai z dapat ditentukan sbb: 0, 25 = (50 -z)/40 Û 0, 025 z = 1, 00 Û z = 40 Sehingga: 38

3. Komposisi semua output Untuk melakukan komposisi semua output fuzzy dilakukan dengan menggunakan metode MAX. Titik potong antara aturan-2 dan aturan-3 terjadi saat m. PBNormal[z]= m. PBBerkurang[z] = (0, 25), yaitu: 0, 25 = 0, 05 z – 1, 5 Û 0, 05 z = 1, 75 Û z = 35 Sehingga: 39

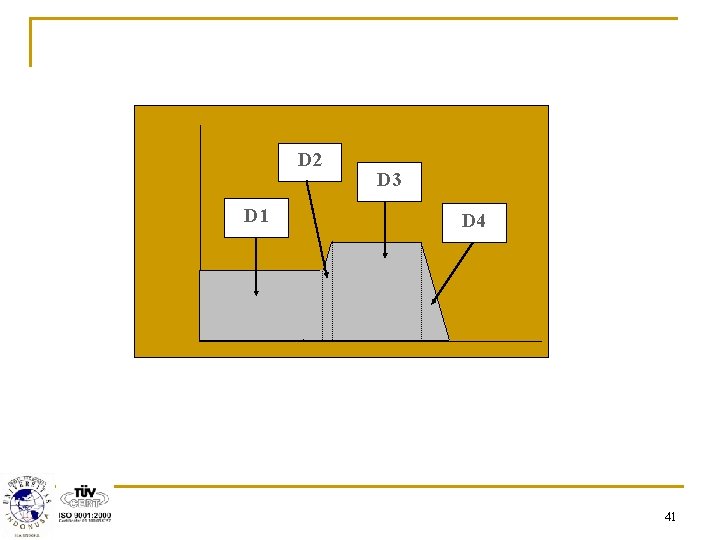
4. Penegasan (Defuzzy) n n Defuzzy dilakukan dengan menggunakan metode Centroid. Untuk menentukan nilai crisp z, dilakukan dengan membagi daerah menjadi 4 bagian (D 1, D 2, D 3, dan D 4) dengan luas masing: A 1, A 2, A 3, dan A 4. Momen terhadap nilai keanggotaan masing-masing adalah: M 1, M 2, M 3 dan M 4. 40

D 2 D 1 D 3 D 4 41

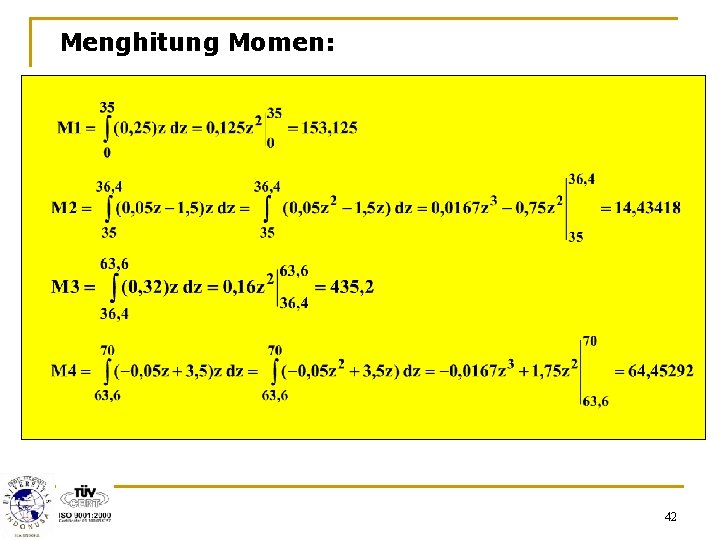
Menghitung Momen: 42

Menghitung Luas: A 1 = 35*0, 25 = 8, 75 A 2 = (0, 25+0, 32)*(36, 4 -35)/2 = 0, 399 A 3 = (63, 6 -36, 4)*0, 32 = 8, 704 A 4 = (70 -63, 6)*0, 32/2 = 1, 024 Menghitung titik pusat (terhadap z): Jadi jumlah minuman yang harus diproduksi tiap harinya sebanyak 35345 kemasan. 43

METODE SUGENO (TSK) n n Penalaran dengan metode SUGENO hampir sama dengan penalaran MAMDANI, hanya saja output (konsekuen) sistem tidak berupa himpunan fuzzy, melainkan berupa konstanta atau persamaan linear. Metode ini diperkenalkan oleh Takagi-Sugeno Kang pada tahun 1985. 44

Model Fuzzy Sugeno Orde-Nol Secara umum bentuk model fuzzy SUGENO Orde-Nol adalah: IF (x 1 is A 1) · (x 2 is A 2) ·. . . · (x. N is AN) THEN z=k dengan Ai adalah himpunan fuzzy ke-i sebagai anteseden, dan k adalah suatu konstanta (tegas) sebagai konsekuen. 45

Model Fuzzy Sugeno Orde-Satu Secara umum bentuk model fuzzy SUGENO Orde-Satu adalah: IF (x 1 is A 1) ·. . . · (x. N is AN) THEN z = p 1*x 1 + … + p. N*x. N + q dengan Ai adalah himpunan fuzzy ke-i sebagai anteseden, dan pi adalah suatu konstanta (tegas) ke-i dan q juga merupakan konstanta dalam konsekuen. 46

CONTOH … n n n Suatu perusahaan makanan kaleng setiap harinya rata menerima permintaan sekitar 55000 kaleng, dan dalam 3 bulan terakhir permintaan tertinggi sebesar 75000 kaleng. Makanan kaleng yang masih tersedia di gudang, setiap harinya rata-rata 7000 kaleng, sedangkan kapasitas gudang maksimum hanya dapat menampung 13000 kaleng. Apabila sistem produksinya menggunakan aturan fuzzy sebagai berikut: 47

[R 1] IF permintaan TURUN And persediaan BANYAK THEN produksi barang = 10000; [R 2] IF permintaan NAIK And persediaan SEDIKIT THEN produksibarang =1, 25*permintaan- persediaan; [R 3] IF permintaan NAIK And persediaan BANYAK THEN produksi barang = permintaan - persediaan; n Tentukanlah berapa jumlah barang yang harus diproduksi hari ini, jika permintaan sebanyak 60000 kaleng, dan persediaan yang masih ada di gudang sebanyak 8000 kaleng. 48

1. Membuat himpunan dan input fuzzy Ada 3 variabel fuzzy yang akan dimodelkan, yaitu: a. Permintaan; terdiri-atas 2 himpunan fuzzy, yaitu: NAIK dan TURUN. b. Persediaan; terdiri-atas 2 himpunan fuzzy, yaitu: BANYAK dan SEDIKIT. c. Produksi Barang 49

A. Variabel Permintaan TURUN NAIK 1 m[x] 0, 5 0, 08 0 0 45 60 75 permintaan per hari (x 1000 kaleng) 50

n Jika Permintaan 60000 maka nilai keanggotaan fuzzy pada tiap-tiap himpunan adalah: q q Himpunan fuzzy TURUN, m. Pmt. Turun[60] = 0, 08. Himpunan fuzzy NAIK, m. Pmt. Naik[60] = 0, 5. diperoleh dari: = 2[(60 -75)/(75 -45)]2 = 0, 5 51

B. Variabel Persediaan SEDIKIT BANYAK 1 m[x] 0, 5 0, 25 0 0 2 5 8 10 11 13 persediaan (x 1000 kemasan per hari) 52

n Jika Persediaan sebanyak 8000 kemasan per hari, maka nilai keanggotaan fuzzy pada tiap himpunan adalah: q Himpunan fuzzy SEDIKIT, m. Psd. Sedikit[8] = 0, 25. diperoleh dari: = (10 -8)/(10 -2) = 0, 25 q Himpunan fuzzy BANYAK, m. Psd. Banyak[8] = 0, 5. diperoleh dari: = (10 -5)/(11 -5) = 0, 5 53

2. Aplikasi operator fuzzy A. Aturan ke-1: [R 1] IF Permintaan TURUN And Persediaan BANYAK THEN Produksi Barang = 10; Operator yang digunakan adalah AND, sehingga: a 1 = m. Predikat. R 1 = min(m. Pmt. Turun[60], m. Psd. Banyak[8]) = min(0, 08; 0, 5) = 0, 08 Produksi barang = 10 54

B. Aturan ke-2: [R 2] IF Permintaan NAIK And Persediaan SEDIKIT THEN Produksi Barang = 1, 25*Permintaan - Persediaan; Operator yang digunakan adalah AND, sehingga: a 2 = m. Predikat. R 2 = min(m. Pmt. Naik[60], m. Psd. Sedikit[8]) = min(0, 5; 0, 25) = 0, 25 Produksi barang = 1, 25*60 – 8 = 67 55

C. Aturan ke-3: [R 3] IF Permintaan NAIK And Persediaan BANYAK THEN Produksi Barang = Permintaan - Persediaan; Operator yang digunakan adalah AND, sehingga: a 3 = = m. Predikat. R 3 min(m. Pmt. Naik[60], m. Psd. Banyak[8]) min(0, 5; 0, 5) 0, 5 Produksi barang = 60 – 8 = 52 56

3. Penegasan (Defuzzy) Jadi produksi barang = 52500 kaleng 57