Fusion Trees Advanced Data Structures Aris Tentes Goal




















- Slides: 22

Fusion Trees Advanced Data Structures Aris Tentes

Goal Fixed Universe Successor Problem l We have a set of n numbers l Each number has a length of at most log u bits (u=size of the fixed Universe) l We want to perform the following actions: 1. Predecessor/Successor 2. Insertion/Deletion in time better than O(log n)

Model Transdichotomous RAM l Memory is composed of words l Each word has a length of w=log u l Each item we store must fit in a word l The following operations require constant time: 1. 2. 3. 4. 5. Addition, Subtraction Multiplication, Division AND, OR, XOR left/right Shift Comparison

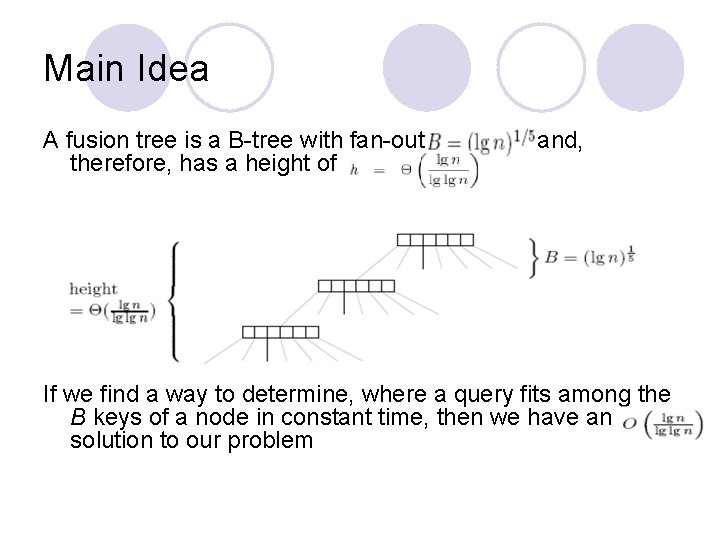
Main Idea A fusion tree is a B-tree with fan-out therefore, has a height of and, If we find a way to determine, where a query fits among the B keys of a node in constant time, then we have an solution to our problem

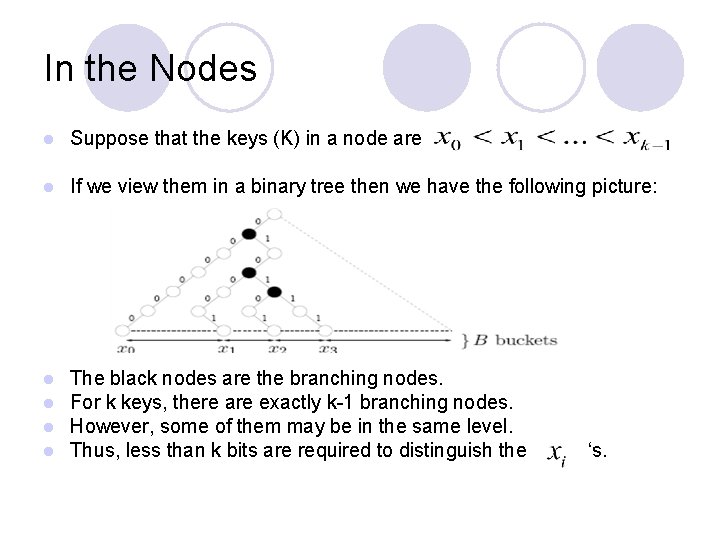
In the Nodes l Suppose that the keys (K) in a node are l If we view them in a binary tree then we have the following picture: l l The black nodes are the branching nodes. For k keys, there are exactly k-1 branching nodes. However, some of them may be in the same level. Thus, less than k bits are required to distinguish the ‘s.

We construct the set B(K) with the branching levels (namely the bit positions required to distinguish the keys) l Let with and l l Def. : Perfect. Sketch(x)= the extracted bits according to B(K) of x. Namely, the bits of x, which correspond to the positions If we collect the perfect sketches of all k keys, then we are able to reduce the node representation to k r-bit strings. l That means that bits would be efficient. Less than a word!! l

l However, computing Perfect. Sketch(x) is difficult. Therefore, we compute an approximation, called Sketch(x). l Sketch(x) contains the same bits with Perfect. Sketch(x), in the same order with some extra 0’s in between, but in consistent positions. l This is done by multiplying x by a number m, which we will see later how we choose it.

Firstly, we compute leaving only the bits which correspond to B(K). l If then we observe that l l All we need is to find an m such that: 1. 2. 3. All are distinct (no collisions) (to preserve order) are concentrated in a small range ( )

l If we find such an m, then we compute which is l Note long. that k sketches fit in a word.

Can we find such an m? l Firstly, we show to find such that whenever l Suppose we have found with the desired property. l We observe that implies l Thus we can choose to be the least residue not represented among the fewer than residues of the form l Then, by adding suitable values of we obtain the final values of mi l

l The set of the sketched keys of a node is denoted by S(K) l Def. : We define the sketch of an entire node as follows:

Lemma l Suppose y is an arbitrary number and xi an element of S (the set of keys). Let be the elements of B(S) and m-1 the most significant bit position in which Perfect. Sketch(y) and Perfect. Sketch(xi) differ. l Assume that p>bm is the most significant position in which y and xi differ. l Then the rank(y) in S is uniquely determined by the interval containing p and the relative order between y and xi.

l Using the previous lemma, we can reduce the computation of rank(y) in K to computing rank(Sketch(y)) in K(S). Having computed rank(Sketch(y)), we have determined the predecessor and successor Sketch(xi) and Sketch(xi+1) of Sketch(y) in K(S). l If xi≤y≤xi+1, then we are done. l Else we pick the one (from the sketched ones) with the longest prefix of significant bits with Sketch(y) and apply the previous lemma. l Use of a look up table. l

Finding the rank(Sketch(y)) in S(K) l Firstly, we compute l Then the substraction l And finally l Observing that .

l Suitable multiplication sums these ones and gives the desired rank. l What remains is to find a way to compute in constant time, the most significant bit, in which two numbers u, v differ. l We can easily see that this problem is reduced to the problem of finding the most significant bit of u XOR v. l We want to compute msb(x).

Lemma l We call a number x d-sparse if the positions of its one bits belong to a set of the form Not all these positions have to be occupied by ones. l If x is d-sparse, then there exist constants y, y’, such that for z=(yx)ANDy’ the i’th bit of z equals the bit in the position of a+di of x. Namely, z is a perfect compression of x.

msb(x) At first consider a partitioning of the w bits of our word x into consecutive blocks of bits. The computation is divided into two phases. 1. We find the leftmost block containing a one and we extract this block 2. We find the leftmost one in this extracted block. l

First Phase l Let be the number, which has ones precisely in the leftmost position of each block, namely and l We compute lead(x)= the leftmost bit of each block is one iff x contains a one in this block. It is given by l We observe that lead(x) is d-sparse, so we can apply the previous lemma and obtain compress(x).

l Let be the set of the first b/s powers of two. l We compute b’=rank(compress(x)) in P, in the same way as before. l Note that b’ identifies the block number (counting from the right ) of the leftmost block of x containing a one.

l The position of the most significant one in lead(x) is f=sb’ l To extract the desired block we multiply by and right justify the significant portion.

Second Phase l We want to find the position of the leftmost one in the extracted block. l As before, we do a rank computation of these s bits with the first s powers of two. l Now we have all the information needed to compute msb(x)

Conclusions l In the static case, the problem of successor and predecessor, is clear to be solvable in time, since this is the height of our B-tree and the computation in each node requires constant time (the data we need is precomputed) l In the dynamic case, the total time to update a node is l The amortized time for insertion/deletion in a Btree is constant. Therefore, sorting requires