Fusion of probabilistic A algorithm and fuzzy inference

Fusion of probabilistic A* algorithm and fuzzy inference system for robotic path planning Rahul Kala, Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior http: //students. iiitm. ac. in/~ipg_200545/ rahulkalaiiitm@yahoo. co. in, rkala@students. iiitm. ac. in Kala, Rahul, Shukla, Anupam, & Tiwari, Ritu (2010) Fusion of probabilistic A* algorithm and fuzzy inference system for robotic path planning, Artificial Intelligence Review, Springer Publishers, Vol. 33, No. 4, pp 275 -306 (Impact Factor: 0. 119) Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

The Problem Inputs ◦ Robotic Map ◦ Location of Obstacles ◦ All Obstacles Static Output ◦ Path P such that no collision occurs Constraints ◦ Time Constraints ◦ Dimensionality of Map ◦ Non-holonomic constraints Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

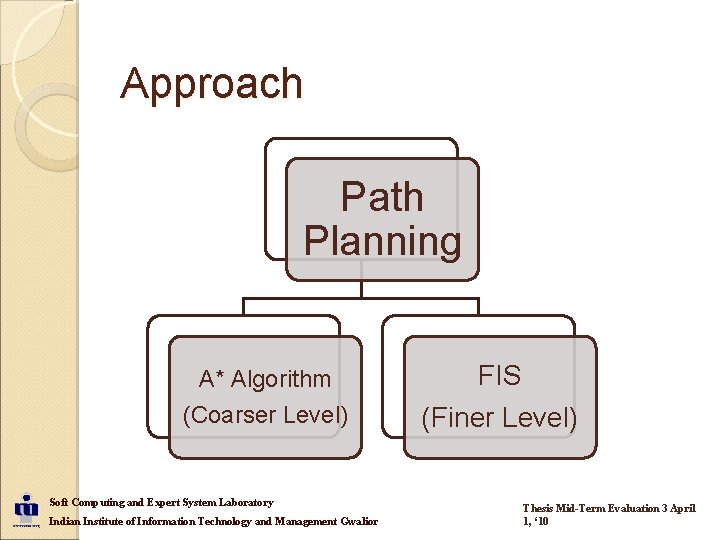
Approach Path Planning A* Algorithm (Coarser Level) Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior FIS (Finer Level) Thesis Mid-Term Evaluation 3 April 1, ‘ 10

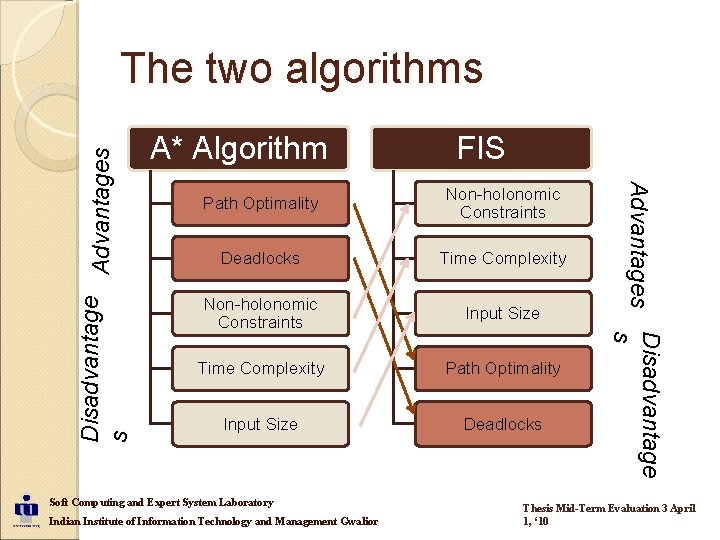
A* Algorithm FIS Path Optimality Non-holonomic Constraints Deadlocks Time Complexity Non-holonomic Constraints Input Size Time Complexity Path Optimality Input Size Deadlocks Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Disadvantage Advantages s The two algorithms Thesis Mid-Term Evaluation 3 April 1, ‘ 10

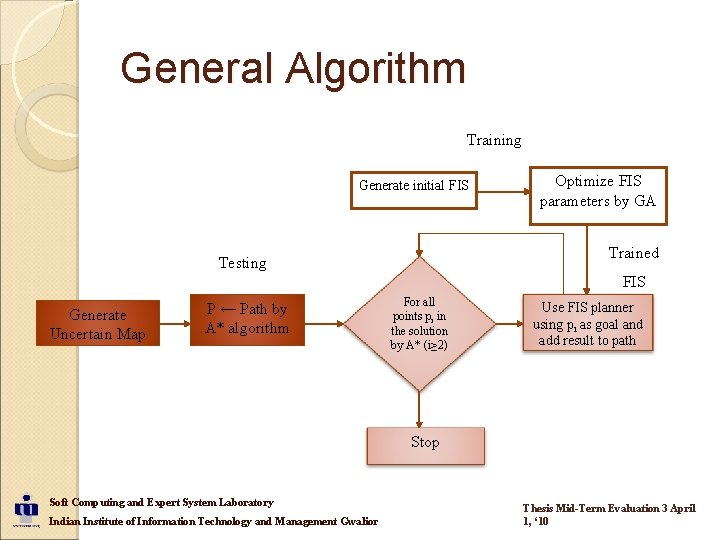
General Algorithm Training Generate initial FIS Optimize FIS parameters by GA Trained Testing FIS Generate Uncertain Map P ← Path by A* algorithm For all points pi in the solution by A* (i≥ 2) Use FIS planner using pi as goal and add result to path Stop Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

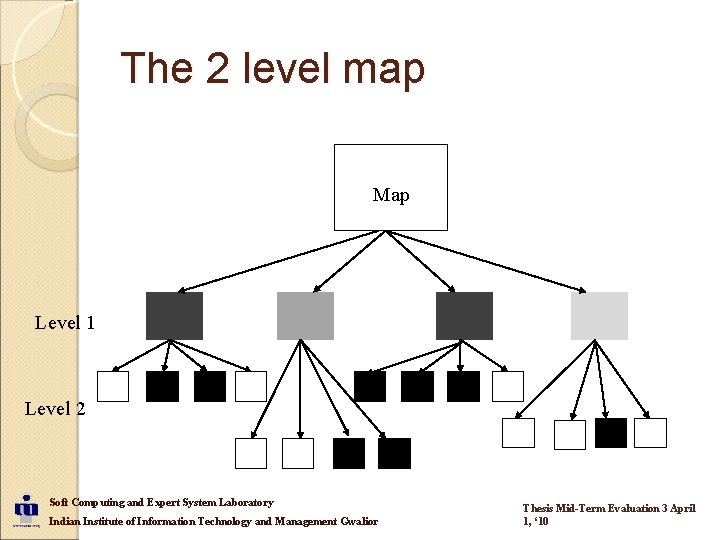
The 2 level map Map Level 1 Level 2 Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

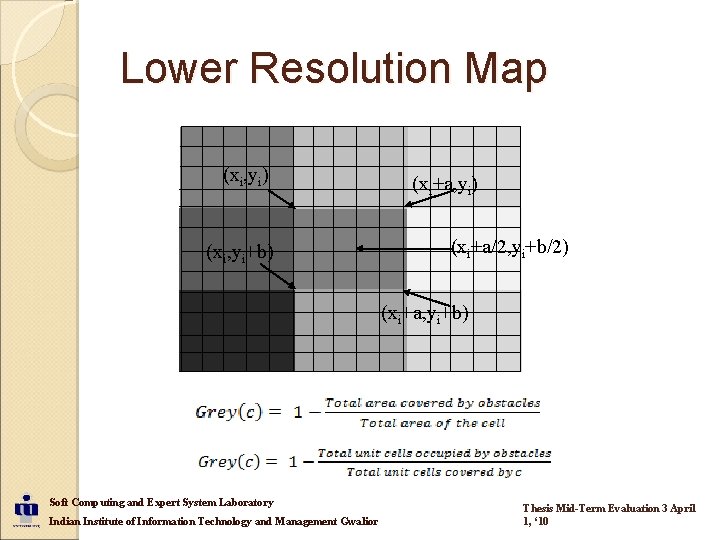
Lower Resolution Map (xi, yi) (xi, yi+b) (xi+a, yi) (xi+a/2, yi+b/2) (xi+a, yi+b) Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

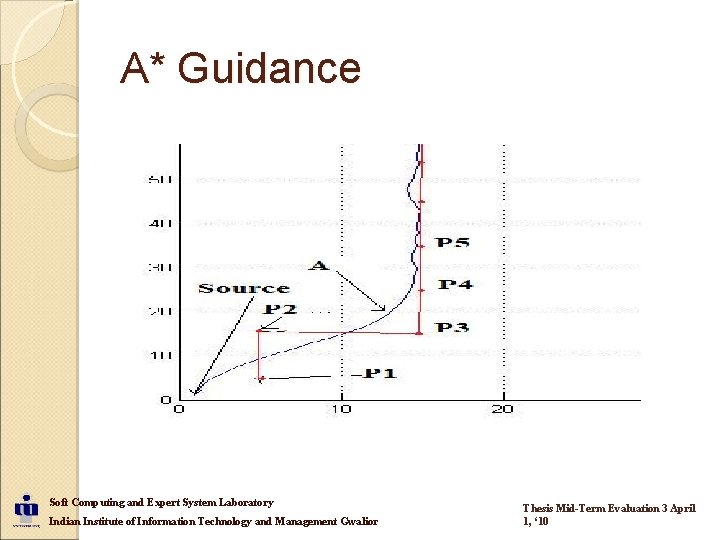
A* Guidance Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

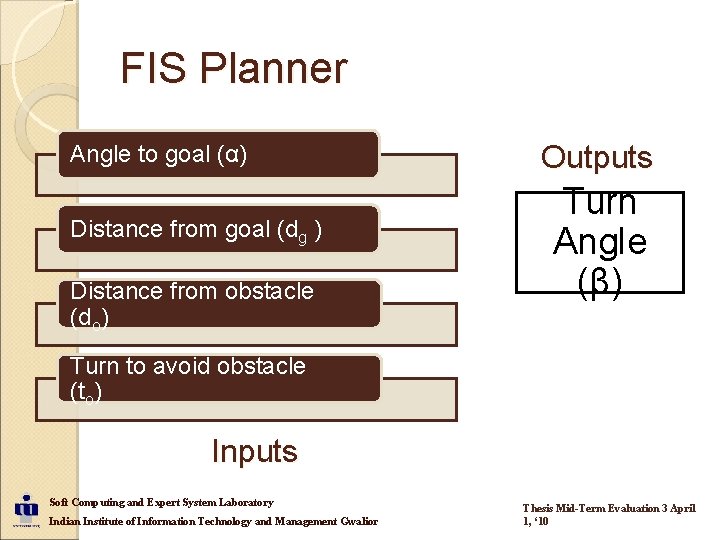
FIS Planner Angle to goal (α) Distance from goal (dg ) Distance from obstacle (do) Outputs Turn Angle (β) Turn to avoid obstacle (to) Inputs Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

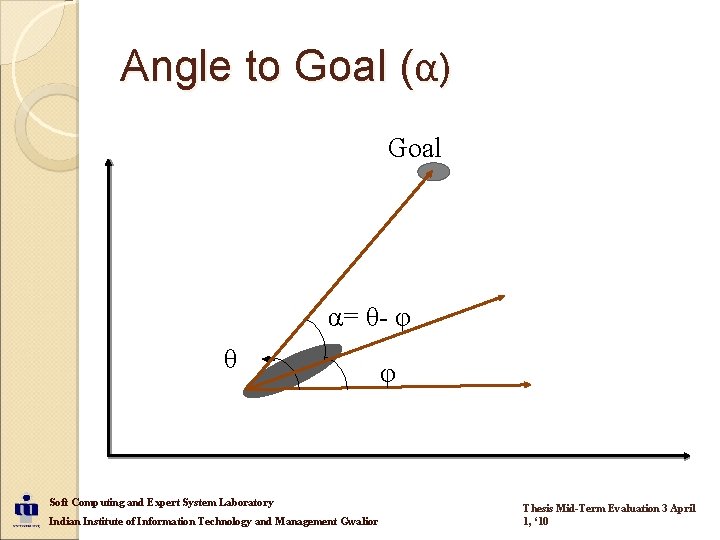
Angle to Goal (α) Goal α= θ- φ θ Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior φ Thesis Mid-Term Evaluation 3 April 1, ‘ 10

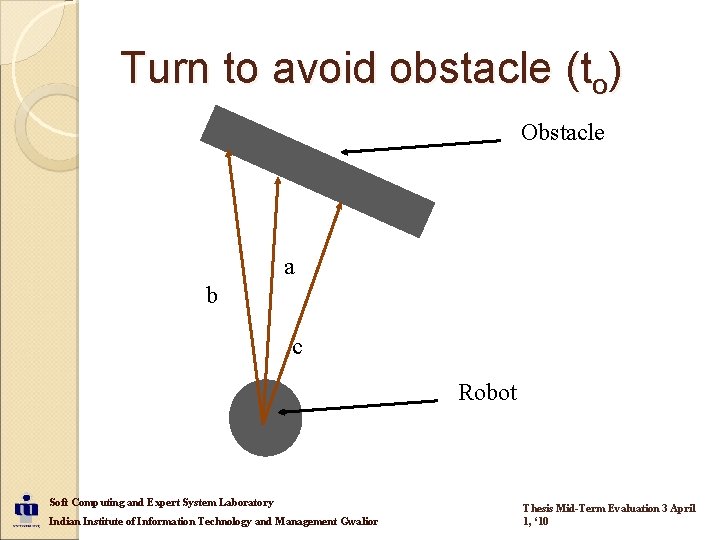
Turn to avoid obstacle (to) Obstacle a b c Robot Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

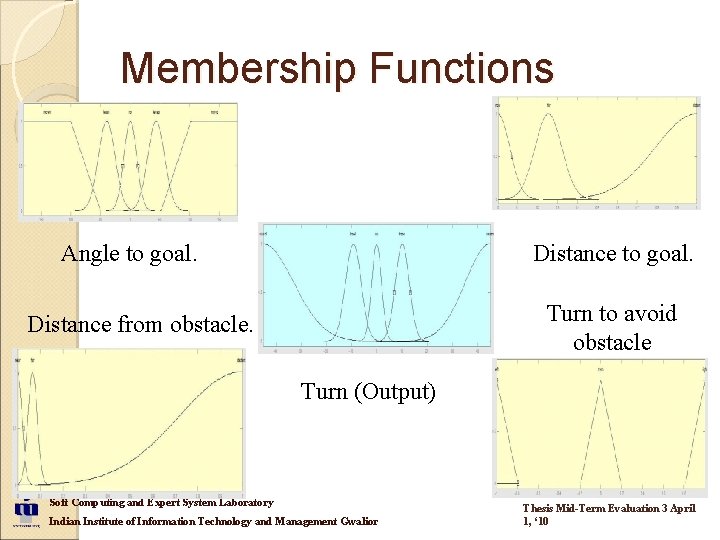
Membership Functions Angle to goal. Distance to goal. Turn to avoid obstacle Distance from obstacle. Turn (Output) Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Rules Rule 1: If (α is less_positive) and (do is not near) then (β is less_right) (1) Rule 2: If (α is zero) and (do is not near) then (β is no_turn) (1) Rule 3: If (α is less_negative) and (do is not near) then (β is less_left) (1) Rule 4: If (α is more_positive) and (do is not near) then (β is more_right) (1) Rule 5: If (α is more_negative) and (do is not near) then (β is more_left) (1) Rule 6: If (do is near) and (to is left) then (β is more_right) (1) Rule 7: If (do is near) and (to is right) then (β is more_left) (1) Rule 8: If (do is far) and (to is left) then (β is less_right) (1) Rule 9: If (do is far) and (to is right) then (β is less_left) (1) Rule 10: If (α is more_positive) and (do is near) and (to is no_turn) then (β is less_right) (0. 5) Rule 11: If (α is more_negative) and (do is near) and (to is no_turn) then Thesis Mid-Term Evaluation 3 April (β is less_left) (0. 5) Indian Institute of Information Technology and Management Gwalior 1, ‘ 10 Soft Computing and Expert System Laboratory

A* Nodal Cost f(n) = h(n) + g(n) C(n) = f(n)* Grey(P) +(1 -Grey(P)) If Grey(P) is 0, it means that the path is not feasible. The fitness in this case must have the maximum possible value i. e. 1 If Grey(P) is 1, it means that the path is fully feasible. The fitness in this case must generalize to the normal total cost value i. e. f(n) Soft Computing and Expert System Laboratory Thesis Mid-Term Evaluation 3 April Information All other cases are intermediate Indian Institute of Technology and Management Gwalior 1, ‘ 10

A* Nodal Cost - 2 To control ‘grayness’ contribution C(n) = f(n)* Grey’(P) +(1 -Grey`(P)) Grey’(P) = 1, if Grey(P) > β Grey(P) otherwise Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

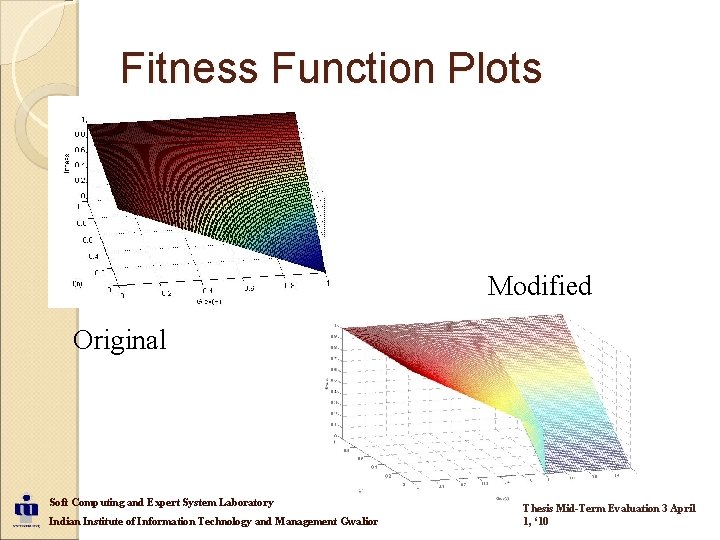
Fitness Function Plots Modified Original Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

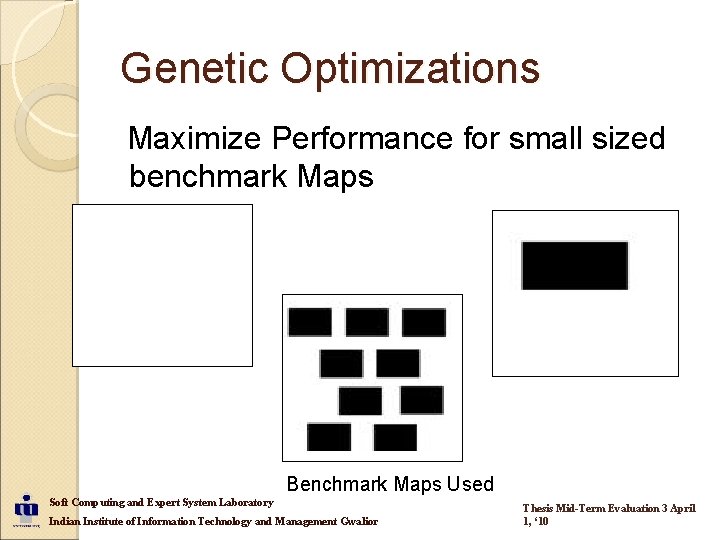
Genetic Optimizations Maximize Performance for small sized benchmark Maps Benchmark Maps Used Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Fitness Function Fi = Li * (1 -Oi) * Ti Li : Total path length Ti : Maximum turn taken any time in the path Oi : Distance from the closest obstacle anytime in the run. F = F 1 + F 2 + F 3 Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

RESULTS

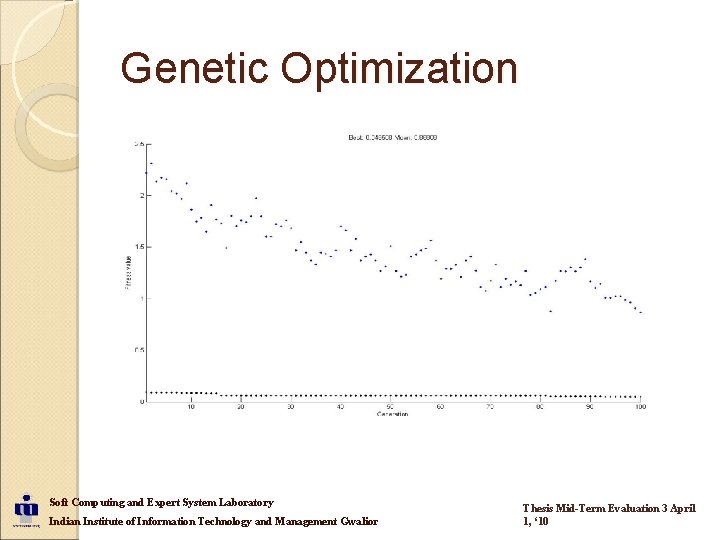
Genetic Optimization Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

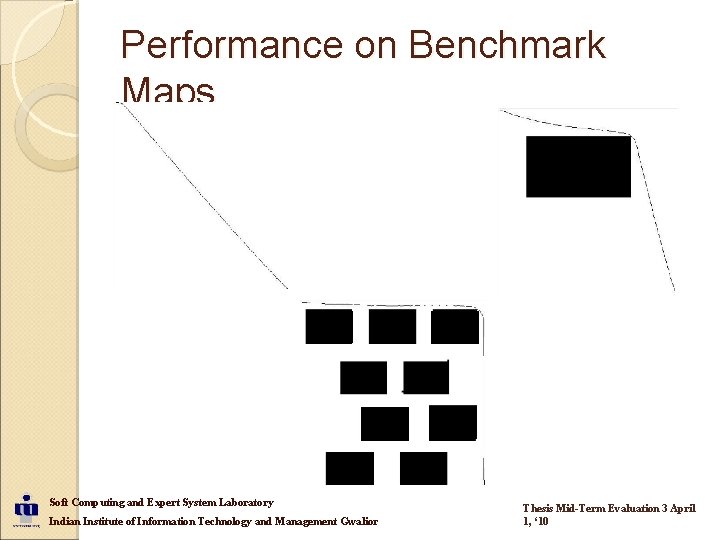
Performance on Benchmark Maps Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

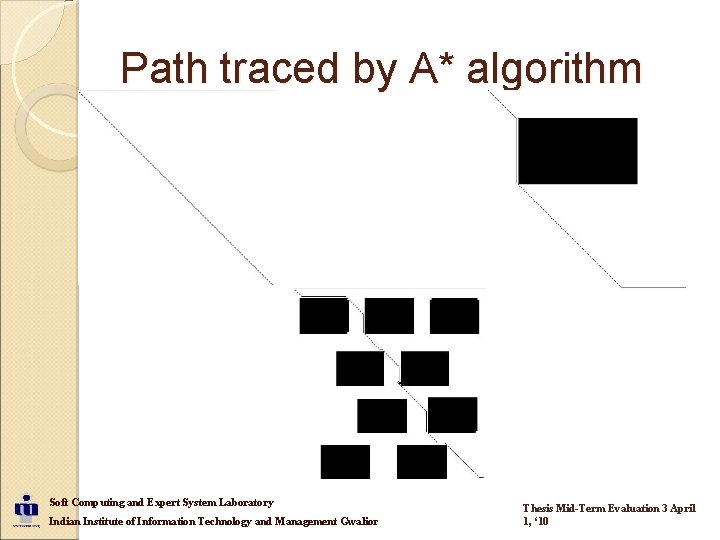
Path traced by A* algorithm Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

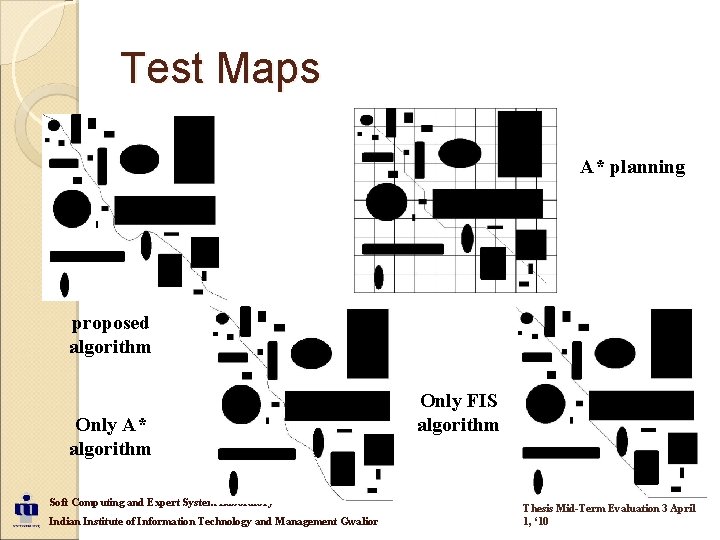
Test Maps A* planning proposed algorithm Only A* algorithm Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Only FIS algorithm Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Test Maps - 2 A* planning proposed algorithm Only A* algorithm Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Only FIS algorithm Thesis Mid-Term Evaluation 3 April 1, ‘ 10

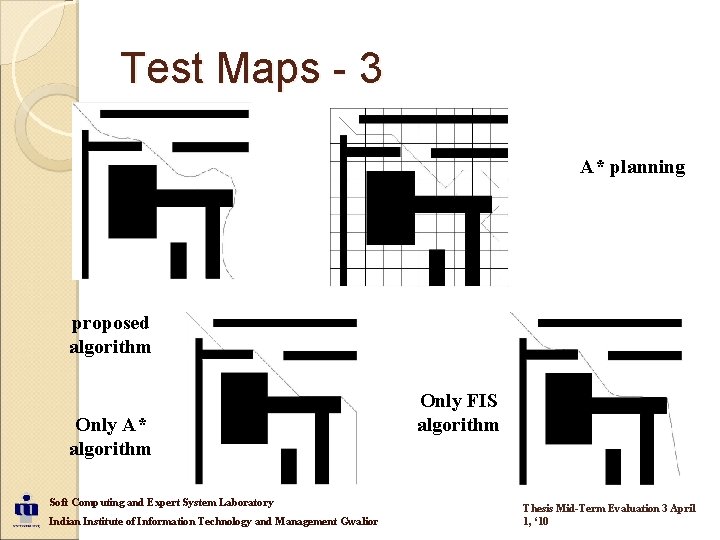
Test Maps - 3 A* planning proposed algorithm Only A* algorithm Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Only FIS algorithm Thesis Mid-Term Evaluation 3 April 1, ‘ 10

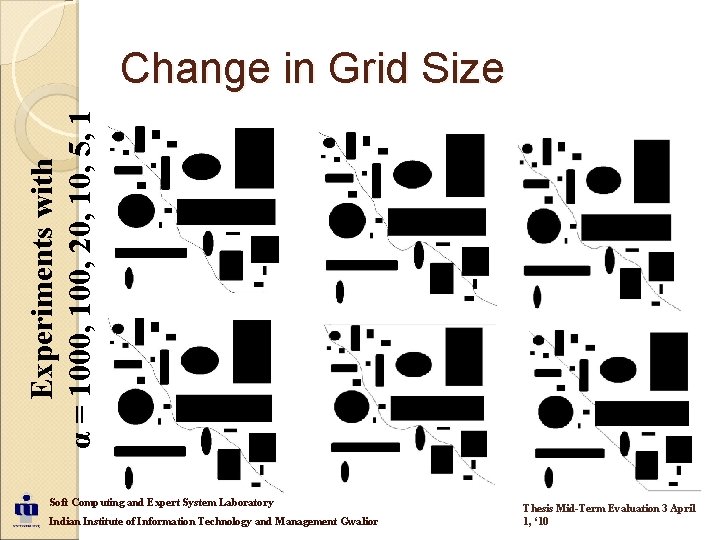
Experiments with α = 1000, 100, 20, 10, 5, 1 Change in Grid Size Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

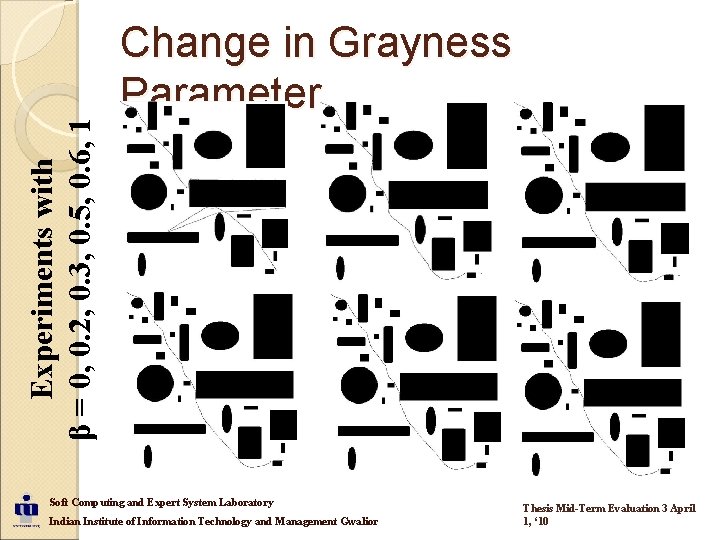
Experiments with β = 0, 0. 2, 0. 3, 0. 5, 0. 6, 1 Change in Grayness Parameter Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Parameter Contribution of the Fuzzy Planner makes path smooth, reduces time. It however may result in a longer path or the failure in finding path Contribution of the A* algorithm reduces path length (α), which can solve very complex maps with most optimal path length at the cost of computational time The contribution of the A* to maximize the probability of the path (β), would usually increase the path length. Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Publication R. Kala, A. Shukla, R. Tiwari (2010) Fusion of probabilistic A* algorithm and fuzzy inference system for robotic path planning. Artificial Intelligence Review. 33(4): 275 -327 Impact Factor: 0. 119 Available at: http: //springerlink. com/content/p 8 w 555 x 67 k 626273/? p=97 dca 405364 84374929 e 0959 d 1 ab 4 dc 3&pi=1 Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

REFERENCES

[1] J. M. Ahuactzin, E. G. Talbi, P. Bessière, E. Mazer, Using Genetic Algorithms for Robot Motion Planning, Lecture Notes In Computer Science 708(1991) 84 – 93. [2] A. Alvarez, A. Caiti, R. Onken, Evolutionary path planning for autonomous underwater vehicles in a variable ocean, IEEE J. Ocean. Eng. 29 (2) (2004) 418 -429. [3] K. M. S. Badran, P. I. Rockett, The roles of diversity preservation and mutation in preventing population collapse in multiobjective genetic programming, In: Proc. 9 th Annual Conf. Genetic and Evolutionary Computation, GECCO’ 07, 2007, pp 1551 – 1558. [4] S. Carpin, E. Pagello, An experimental study of distributed robot coordination, Robotics and Autonomous Systems 57(2) (2009) 129 -133. [5] L. H. Chen, C. H. Chiang, New approach to intelligent control systems with self-exploring process, IEEE Trans. Systems, Man, and Cybernetics, Part B: Cybernetics 33 (1) (2003) 56 -66. [6] J. Cortes, L. Jaillet, T. Simeon, Disassembly Path Planning for Complex Articulated Objects, IEEE Trans. Robotics, 24(2) (2008) 475 -481. [7] P. Dittrich, A. Bürgel, W. Banzhaf, Learning to move a robot with random morphology, Lecture Notes in Computer Science 1468(1998) 165178. [8] L. Doitsidis, N. C. Tsourveloudis, S. Piperidis, Evolution of Fuzzy Controllers for Robotic Vehicles: The role of Fitness Function Selection, J. Intelligent and Robotic Systems (2009). [9] S. Garrido, L. Moreno, D. Blanco, Exploration of 2 D and 3 D Environments using Voronoi Transform and Fast Marching Method, J. Intelligent and Robotic Systems 55(1) (2009) 55 – 80. [10] W. Han, S. Baek, T. Kuc, GA Based On-Line Path Planning of Mobile Robots Playing Soccer Games, In: Proc. 40 th Midwest Symposium Circuits and Systems, 1(1) (1997). [11] N. Hazon, G. A. Kaminka, On redundancy, efficiency, and robustness in coverage for multiple robots, Robotics and Autonomous Systems 56(12) (2008) pp 1102 -1114. [12] N. B. Hui, D. K. Pratihar, A comparative study on some navigation schemes of a real robot tackling moving obstacles, Robotics and Computer-Integrated Manufacturing 25(4 -5)(2009) 810 -828. [13] G. E. Jan, Y. C. Ki, L. Parberry, Optimal Path Planning for Mobile Robot Navigation, IEEE/ASME Trans. Mechatronics, 13(4)(2008) 451 -460. [14] K. G. Jolly, R. S. Kumar, R. Vijayakumar, A Bezier curve based path planning in a multi-agent robot soccer system without violating the acceleration limits, Robotics and Autonomous Systems 57(1)(2009) 23 -33. [15] C. F. Juang, A hybrid of genetic algorithm and particle swarm optimization for recurrent network design, IEEE Trans. Systems, Man, and Cybernetics Part B: Cybernetics, 34(2) (2004) 997 -1008. [16] R. Kala, A. Shukla, R. Tiwari, S. Rungta, R. R. Janghel, Mobile Robot Navigation Control in Moving Obstacle Environment using Genetic Algorithm, Artificial Neural Networks and A* Algorithm, In: IEEE Proc. World Congress Computer Science and Information Engineering, CSIE ‘ 09, 2009, pp 705 -713. [17] S. Kambhampati, L. Davis, Multiresolution path planning for mobile robots 2(3)(1986) 135 -145. [18] K. J. O' Hara, D. B. Walker, T. R. Balch, Physical Path Planning Using a Pervasive Embedded Network, IEEE Trans. Robotics 24(3)(2008) 741 -746. [19] T. Peram, K. Veeramachaneni, C. K. Mohan, Fitness-distance-ratio based particle swarm optimization, In: Proc. 2003 IEEE Swarm Intelligence Symp. , SIS '03, 2003, pp. 174 -181. [20] S. Patnaik, L. C. Jain, S. G. Tzafestas, G. Resconi, A. Konar, Innovations in Robot Mobility and Control, Springer, 2005. [21] M. Peasgood, C. M. Clark, J. Mc. Phee, A Complete and Scalable Strategy for Coordinating Multiple Robots Within Roadmaps, IEEE Trains. Robotics 24(2)(2008) 283 -292. Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

[22] C. Pozna, F. Troester, R. E. Precup, J. K. Tar, S. Preitl, On the design of an obstacle avoiding trajectory: Method and simulation, Mathematics and Computers in Simulation 79(7)(2009) 2211 -2226. [23] S. K. Pradhan, D. R. Parhi, A. K. Panda, Fuzzy logic techniques for navigation of several mobile robots, Applied Soft Computing 9(1) (2009) 290 -304. [24] N. Sadati, J. Taheri, Genetic algorithm in robot path planning problem in crisp and fuzzified environments, In: Proc. 2002 IEEE Int. Conf. Industrial Technology, ICIT '02, 2002, vol. 1, 2002, pp. 175 -180. [25] K. H. Sedighi, K. Ashenayi, T. W. Manikas, R. L. Wainwright, H. M. Tai, Autonomous local path planning for a mobile robot using a genetic algorithm, Cong. Evolutionary Computation, CEC’ 04, 2004, vol. 2, 2004, pp. 1338 -1345. [26] T. Shibata, T. Fukuda, K. Kosuge, F. Arai, Selfish and coordinative planning for multiple mobile robots by genetic algorithm, In: Proc. 31 st IEEE Conf. Decision and Control, 1992, Vol. 3, 1992, pp. 2686 -2691. [27] A. Shukla, R. Tiwari, R. Kala, Mobile Robot Navigation Control in Moving Obstacle Environment using A* Algorithm, In: Proc. Intl. Conf. Artificial Neural Networks in Engg. , ANNIE’ 08, ASME Publications, Vol. 18, 2008, pp 113 -120. [28] S. Squillero, A. P. Tonda, A novel methodology for diversity preservation in evolutionary algorithms, In: Proc. 2008 Conf. companion on Genetic and Evolutionary Computation, GECCO’ 08, 2008, pp 2223 -2226. [29] A. Sud, E. Andersen, S. Curtis, M. C. Lin, D. Manocha, Real-Time Path Planning in Dynamic Virtual Environments Using Multiagent Navigation Graphs, IEEE Trans. Visualization and Computer Graphics 14(3) (2008) 526 -538. [30] K. Sugihara, J. Yuh, GA-Based Motion Planning For Underwater Robotic Vehicles, In: Proc. 10 th International Symp. on Unmanned Untethered Submersible Technology, Autonomous Undersea Systems Institute, 1996, pp 406— 415. [31] R. Toogood, H. Hong , W. Chi, Robot Path Planning Using Genetic Algorithms, In: Proc. IEEE Int. Conf. Systems, Man and Cybernetics, 1995. Intelligent Systems for the 21 st Century, Vol. 1, 1995, pp 489 -494. [32] C. H. Tsai, J. S. Lee, J. H. Chuang, Path planning of 3 -D objects using a new workspace model, IEEE Trans. Systems, Man, and Cybernetics, Part C: Applications and Reviews 31(3)(2001) 405 -410. [33] J. Tu, S. Yang, Genetic algorithm based path planning for a mobile robot, In: Proc. of IEEE Intl. Conf. Robotics and Automation, ICRS’ 03, Vol. 1, 2003, pp 1221 -1226. [34] C. Urdiales, A. Bandera, F. Arrebola, F. Sandoval, Multi-level path planning algorithm for autonomous robots, IEEE Electronics Letters 34(2)(1998) 223 -224. [35] K. Veeramachaneni, T. Peram, C. Mohan, L. A. Osadciw, Optimization Using Particle Swarms with Near Neighbor Interactions, In: Proc. Genetic and Evolutionary Computation, GECCO ‘ 03, vol 2723, 2003, pp 110 -121. [36] C. Wang, Y. C. Soh, H. Wang, A hierarchical genetic algorithm for path planning in a static environment with obstacles, In: Proc. IEEE Canadian Conf. Electrical and Computer Engineering, CCECE ’ 02, 2002, vol. 3, pp. 1652 -1657. [37] J. Xiao, Z. Michalewicz, Z. Lixin, K. Trojanowski, Adaptive evolutionary planner/navigator for mobile robots, IEEE Trans. Evolutionary Computation 1(1) (1997)18 -28. [38] S. X. Yang, M. Meng, An efficient neural network approach to dynamic robot motion planning, Neural Networks 13(2)(2000) 143 -148. [39] D. J. Zhu, J. C. Latombe, New heuristic algorithms for efficient hierarchical path planning , IEEE Trans. Robotics and Automation 7(1)(1991) 9 -20. [40] S. X. Yang, M. Meng, An efficient neural network approach to dynamic robot motion planning, Neural Networks 13 (2000) 143– 148 [41] AR Willms, S X Yang, An Efficient Dynamic System for Real-Time Robot-Path Planning, IEEE Trans on Systems Man and Cybernetics – Part B Cybernetics, 36(4) (2006) 755 -766 [42] S. Grossberg, “Contour enhancement, short term memory, and constancies in reverberating neural networks, ” Studies in Applied Mathematics, (3)(1973) 217– 257 Soft Computing and 52 Expert System Laboratory Thesis Mid-Term Evaluation 3 April [43] A. Zelinsky, “Using path transforms to guide the search for findpath in 2 d, ” Int. J. of Robotic Research, 13(4)(1994) 315– 325 Indian Institute of Information Technology and Management Gwalior 1, ‘ 10

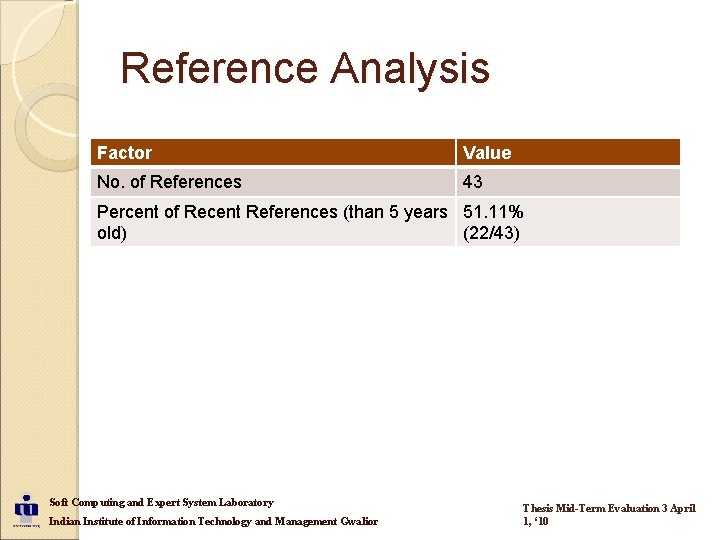
Reference Analysis Factor Value No. of References 43 Percent of Recent References (than 5 years 51. 11% old) (22/43) Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10

Thank You Soft Computing and Expert System Laboratory Indian Institute of Information Technology and Management Gwalior Thesis Mid-Term Evaluation 3 April 1, ‘ 10