Further Pure 1 Lesson 3 Inverse Matrices Reminder





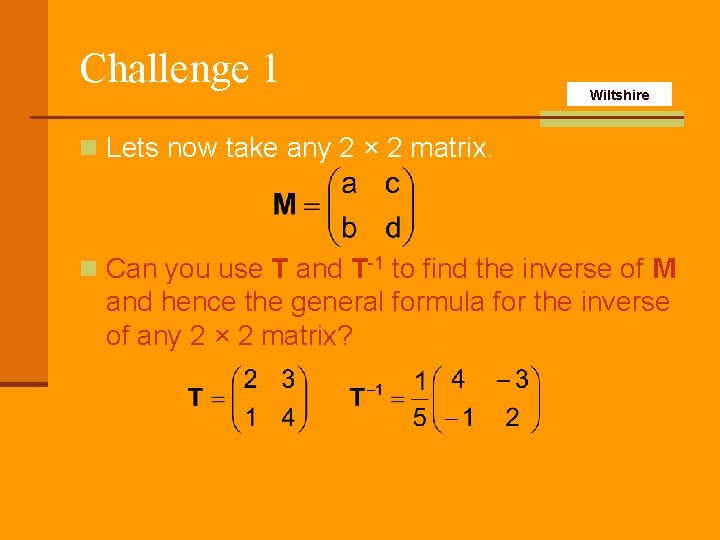
















- Slides: 22

Further Pure 1 Lesson 3 – Inverse Matrices

Reminder from lesson 1 Wiltshire n Note that any matrix multiplied by the identity matrix is itself. n And any matrix multiplied by the zero matrix is the zero matrix.

Inverse Matrix Wiltshire n All operations have an opposite. n We discussed in lesson 2 about using matrices to n n perform transformations. An inverse matrix will undo the transformation and return you to where you started. If a matrix is called A, then its inverse is known as A-1. In lesson 1 we briefly met the concept of an identity matrix (seen on first slide). So if multiplying A by A-1 returns you to where you started and multiplying by the identity matrix leaves you where you are, we can conclude that AA-1 = A-1 A = I

Challenge 1 Wiltshire n You need to know the general formula for the inverse of a 2 × 2 matrix. n Can you find the inverse to the following matrix? n Use the property TT-1 = I n From this we can form 2 pairs of simultaneous equations. 2 p + 3 q = 1 p + 4 q = 0 2 r + 3 s = 0 r + 4 s = 1

Challenge 1 n The solutions to these equations are n So the inverse of T is Wiltshire
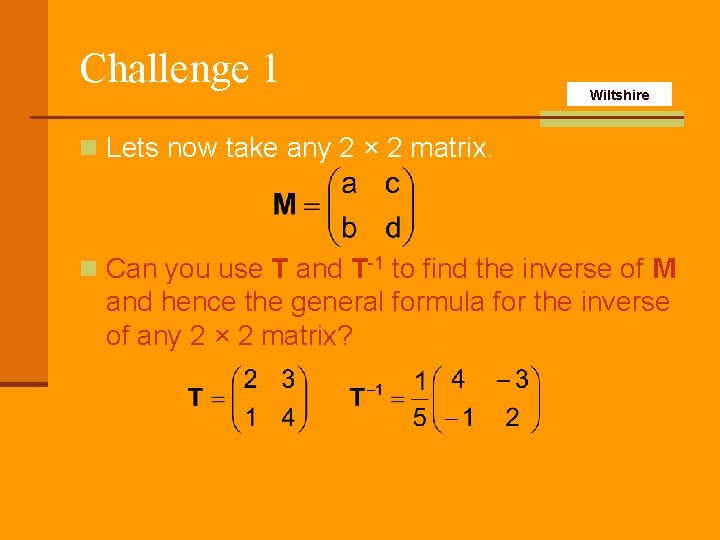
Challenge 1 Wiltshire n Lets now take any 2 × 2 matrix. n Can you use T and T-1 to find the inverse of M and hence the general formula for the inverse of any 2 × 2 matrix?

The Determinant of a 2 × 2 matrix Wiltshire n We have just found the general equation for the inverse of any 2 × 2 matrix. n The Δ symbol is a capital delta and will always be a numerical value. n The value can be calculated from the matrix and is known as the determinant of the matrix. n Using T and T-1 can you spot how to calculate it?

The Determinant of a 2 × 2 matrix Wiltshire n To calculate the determinant of a matrix M you multiply a by d and subtract b by c. n Below is the official notation. n If the det is zero then the inverse does not exist and the matrix is known as singular. n If the det is not zero then the inverse does exist and the matrix is known as non-singular. n Note: Only square matrices have inverses.

Challenge 2 Wiltshire n This is above the scope of the course and not required for you to do. n However it is a challenging question that will test your algebraic manipulation skills. n Can you find the inverse of M using the identity below and the method we used a few slides ago. n This will also prove where the formula for the determinant comes from.

Questions Wiltshire n Find the inverse of the following matrices.

Inverse of a product Wiltshire n Find the inverse of AB. n Lets call the inverse of AB, X. n So as we already know X(AB) = I n First multiply by B-1 X(AB)B-1 = I×B-1 XA = B-1 n Next multiply by A-1 XAA-1 = B-1 A-1 X = B-1 A-1 n This is an important result that you need to know (AB)-1 = B-1 A-1

Properties of the determinant Wiltshire n The orange square is an enlargement of the black square by a scale n n n n n factor 2. What is the area of the object? Area = 9 units 2 What is the area of the image? Area = 36 units 2 The transformation performed can be described by the following matrix What do you notice about the determinant of the matrix and the enlargement shown. The determinant of a matrix indicates the scale factor of the area of enlargement. The det T is known as the signed scale factor as it can be negative. The negative signifies that the rotation direction has been reversed.

Task n Can you explain how we know that the area of any shape rotated θ degrees anti-clockwise about the origin remains the same. Wiltshire

Matrices with det = 0 Wiltshire n The determinant of a matrix tells us the scale factor of the areas` enlargement. n What would be the area of a shape transformed by a matrix with det = 0? n The area would be 0. n All the points will have been transformed so what will the image look like? n The image will be a straight line. n We can see an example of this on the next slide.

Example 1 n Lets start with a rectangle on a 2 D pair of axes. n We can write the co-ordinates of the vertices in matrix form. n Next transform the object using a matrix with a det = 0 n The image becomes a series of points that are in a straight line. Wiltshire

Example 1 n In fact although we used a rectangle for the example any point in the plane will transform to the line. n From the diagram its clear to see what the equation of the line will be. n y=x Wiltshire

Example 1 n We can reach the same result n n n as the last slide using an algebraic method. Lets look at the general coordinate (x, y). Under the transformation we get the co-ordinates (x`, y`) Using matrix multiplication we can see that. x + 2 y = x` x + 2 y = y` From this we get y` = x + 2 y = x` Or y = x Wiltshire

Example 2 Wiltshire n The plane is transformed by the matrix. n Show that the whole plane is mapped to a straight line and find the equation of this line. n Using matrix multiplication gives us the simultaneous equations. x` = 2 x – y y` = -4 x + 2 y n From the equations we get y` = -2(2 x – y) = -2 x` n All the points will map to the line y = -2 x

Example 2 Wiltshire n All points in a plane transform to a straight line. n This is because there are infinitely many lines that transform to a single point.

Example 3 Wiltshire n For the matrix T find the equation of the line of points that map to (5, -10). n We use matrix multiplication to find what equations will be equal to the co-ordinate (5, -10) n This gives us the equations 2 x – y = 5 -4 x + y = -10 n These two equations give the exact same information. 2 x – y = 5

Summary 1 n The inverse of a matrix n Is n Where Wiltshire

Summary 2 n MM-1 = M-1 M = I n X = B-1 A-1 Wiltshire