Funkce Pojem funkce Dostupn z Metodickho portlu www

Funkce Pojem funkce Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Funkce • vyjadřuje závislost dvou veličin • veličiny z oblasti fyziky, biologie, statistiky, různé obory techniky, … • závislost lze vyjádřit graficky (graf), rovnicí nebo tabulkou Úkol: Uveďte příklady závislosti dvou veličin. Např. : závislost dráhy na čase, hmotnost tělesa na jeho objemu (fyzika), závislost obsahu čtverce na délce jeho strany, ….

Funkce - příklady 1. Sestavte tabulku závislosti obsahu obdélníku na délce jeho jedné strany. Platí S = a. b, a = 6 cm, b {1, 2, 3, 4, 5, 7, 8, 9, 10 cm}. b 1 2 3 4 5 7 8 9 10 6 12 18 24 30 42 48 54 60 (cm) S (cm 2)

Funkce - příklady 2. Sestavte tabulku závislosti dráhy s ujeté autem na čase t, víte-li, že průměrná rychlost auta v = 75 km/h a pro čas t platí t {1, 2, 3, 4, 5, 6 h}. Rovnice: s=v. t s = 75. t t (h) 1 2 3 4 5 6 s (km) 75 150 225 300 375 450

Funkce - příklady 3. Sestavte tabulku závislosti ceny hrnečků y na počtu koupených kusů x, víte-li, že jeden hrneček stojí 25 Kč a pro počet kusů x platí x {1, 2, 5, 8, 10, 20}. Rovnice: y = 25. x x 1 2 5 8 10 20 y 25 50 125 200 250 500

Funkce - definice • Funkce f je takový předpis, který ke každému reálnému číslu x (dané množiny D) přiřazuje právě jedno reálné číslo. • Množinu D nazýváme definiční obor funkce f. Funkce f je dána: Øvzorcem (rovnicí) Øtabulkou Øgrafem

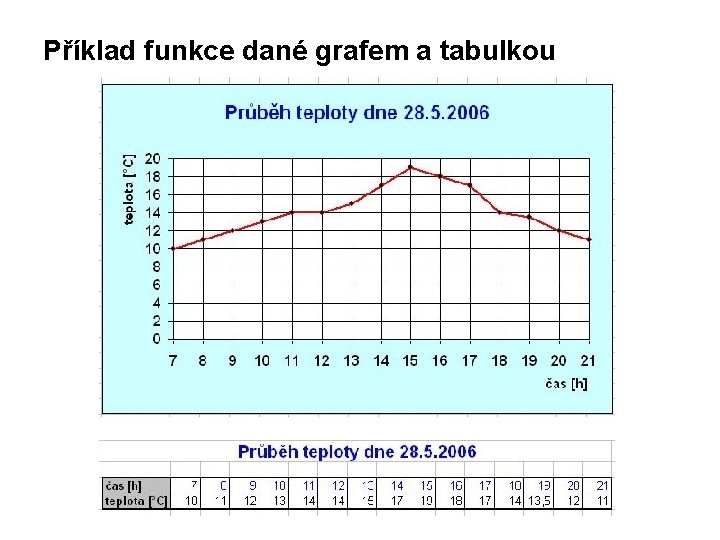
Příklad funkce dané grafem a tabulkou

Funkce - zápis Funkci zapisujeme: f: x y, x D (čteme: prvku x množiny D je přiřazeno funkcí f reálné číslo y) nebo: y = f(x), x D (čteme: prvku x množiny D je přiřazeno funkcí f reálné číslo y)

Funkce - pojmy • proměnná x = nezávisle proměnná • proměnná y = závisle proměnná • množina D = definiční obor (množina všech reálných čísel - x, je dána s funkcí) • množina H = množina hodnot funkce (množina všech reálných čísel - y, která jsou danou funkcí f přiřazena prvkům jejího definičního oboru - x)

Funkce - graf Grafem funkce y = f(x), x D nazýváme množinu všech bodů roviny, které mají souřadnice [x, y]

Funkce - příklady 1. Zapište alespoň deset hodnot funkcí: a) y = x 2 + 1, D = R c) b) 2. Sestrojte graf funkce: a) y = 2 x, D = {-2, -1, 0, 1, 2} b) y = 2 x, D = R 3. Sestrojte na milimetrový papír grafy funkcí ze cvičení 1.

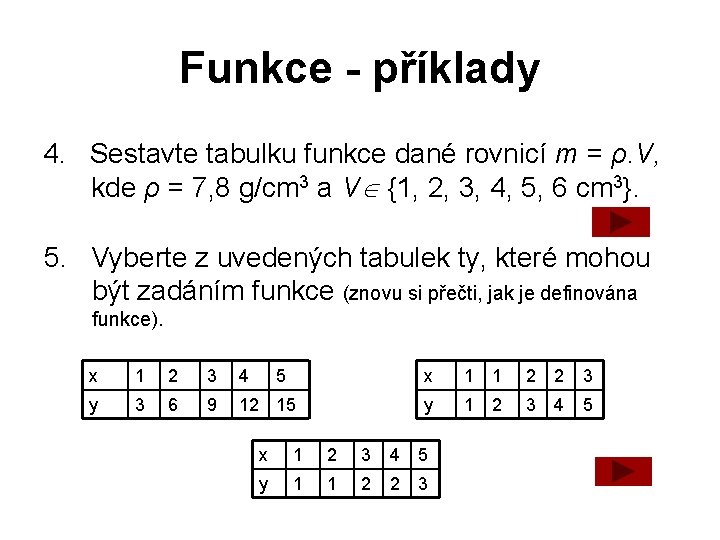
Funkce - příklady 4. Sestavte tabulku funkce dané rovnicí m = ρ. V, kde ρ = 7, 8 g/cm 3 a V {1, 2, 3, 4, 5, 6 cm 3}. 5. Vyberte z uvedených tabulek ty, které mohou být zadáním funkce (znovu si přečti, jak je definována funkce). x 1 2 3 4 5 y 3 6 9 12 15 x 1 1 2 2 3 y 1 2 3 4 5 x 1 2 3 4 5 y 1 1 2 2 3

Konec úvodu o funkcích

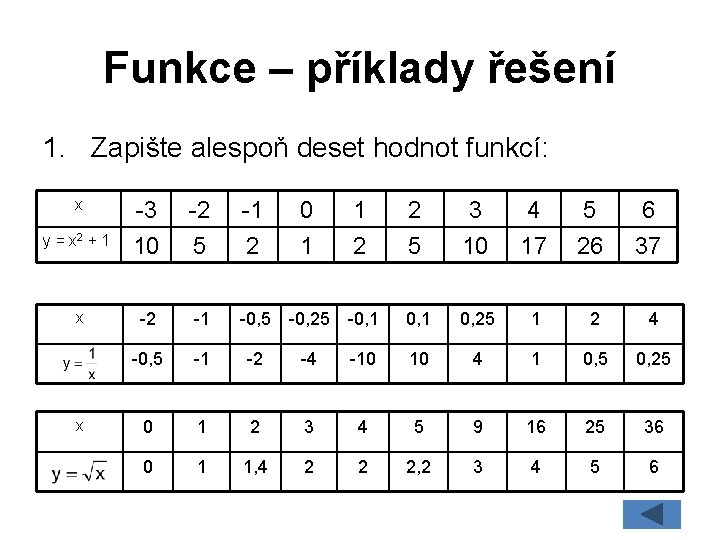
Funkce – příklady řešení 1. Zapište alespoň deset hodnot funkcí: x y = x 2 + 1 x x -3 10 -2 5 -1 2 0 1 1 2 2 5 3 10 4 17 5 26 6 37 -2 -1 -0, 5 -0, 25 -0, 1 0, 25 1 2 4 -0, 5 -1 -2 -4 -10 10 4 1 0, 5 0, 25 0 1 2 3 4 5 9 16 25 36 0 1 1, 4 2 2 2, 2 3 4 5 6

Funkce – příklady řešení 2. Sestrojte graf funkce: x -2 -1 0 1 2 x -4 -3 -2 -1 0 1 2 3 4 y = 2 x -4 -2 0 2 4 y = 2 x -8 -6 -4 -2 0 2 4 6 8 -4 -3 -2 -1 y y 5 4 3 2 1 0 -1 -2 -3 -4 -5 1 2 3 4 x -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 3 4 x

Funkce – příklady řešení 4. Sestavte tabulku funkce dané rovnicí m = ρ. V, kde ρ = 7, 8 g/cm 3 a V {1, 2, 3, 4, 5, 6 cm 3}. V (cm 3) m (kg) 1 7, 8 2 15, 6 3 23, 4 4 31, 2 5 39 6 46, 8

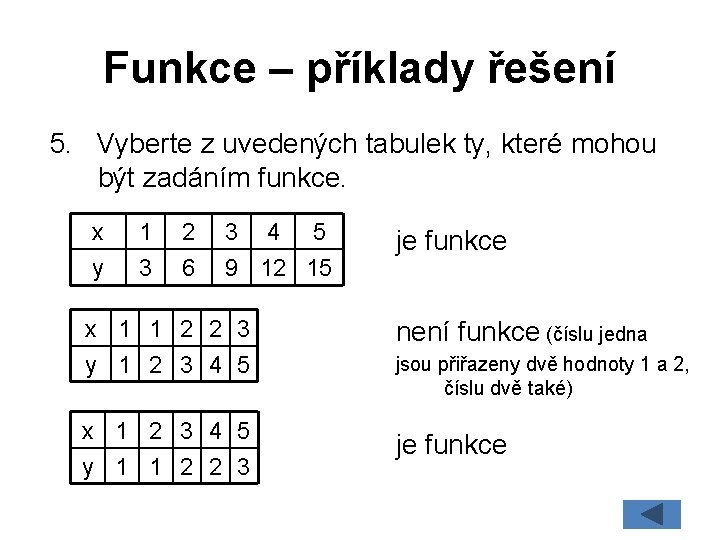
Funkce – příklady řešení 5. Vyberte z uvedených tabulek ty, které mohou být zadáním funkce. x y 1 3 2 6 3 4 5 9 12 15 je funkce x 1 1 2 2 3 y 1 2 3 4 5 není funkce (číslu jedna x 1 2 3 4 5 y 1 1 2 2 3 je funkce jsou přiřazeny dvě hodnoty 1 a 2, číslu dvě také)