FUNGSI Pertemuan Ke5 Tujuan Instruksional Khusus Memahami konsep

FUNGSI Pertemuan Ke-5

Tujuan Instruksional Khusus Memahami konsep fungsi pada himpunan p Memahami macam-macam fungsi p Memahami tentang invers dan komposisi fungsi p

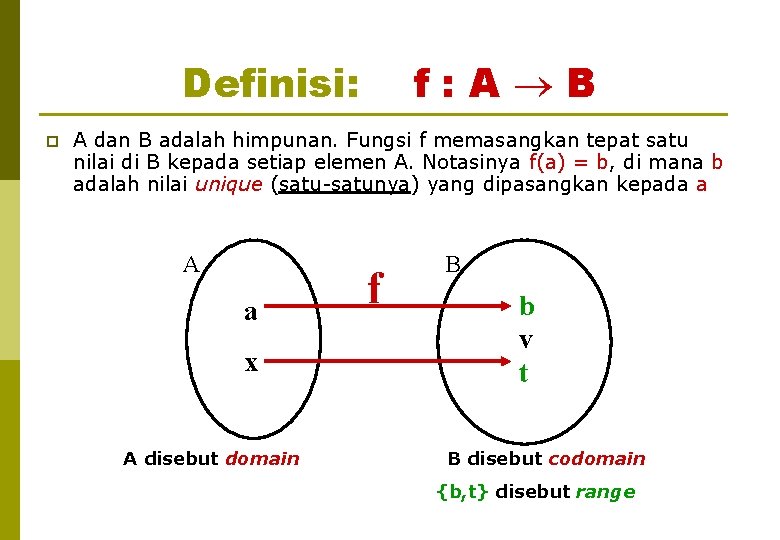
Definisi: p f: A B A dan B adalah himpunan. Fungsi f memasangkan tepat satu nilai di B kepada setiap elemen A. Notasinya f(a) = b, di mana b adalah nilai unique (satu-satunya) yang dipasangkan kepada a A a x A disebut domain f B b v t B disebut codomain {b, t} disebut range

Syarat Fungsi f : A B p Pada A : n n p Tiap elemen pada A harus ada pasangan di B Tidak boleh ada cabang Pada B : n n Elemen pada B boleh tidak ada pasangan Boleh ada cabang

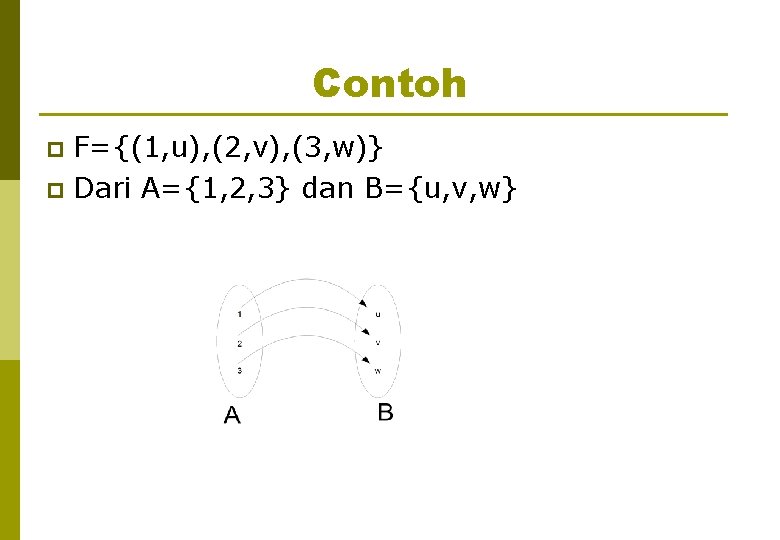
Contoh F={(1, u), (2, v), (3, w)} p Dari A={1, 2, 3} dan B={u, v, w} p

Contoh F={(1, u), (2, v), (3, w)} p Dari A={1, 2, 3, 4} dan B={u, v, w} p p f bukan fungsi, karena ada elemen pada A yang tidak ada pasangannya

Contoh F={(1, u), (1, v)(2, v), (3, w)} p Dari A={1, 2, 3} dan B={u, v, w} p p f bukan fungsi, karena ada elemen pada A yang bercabang

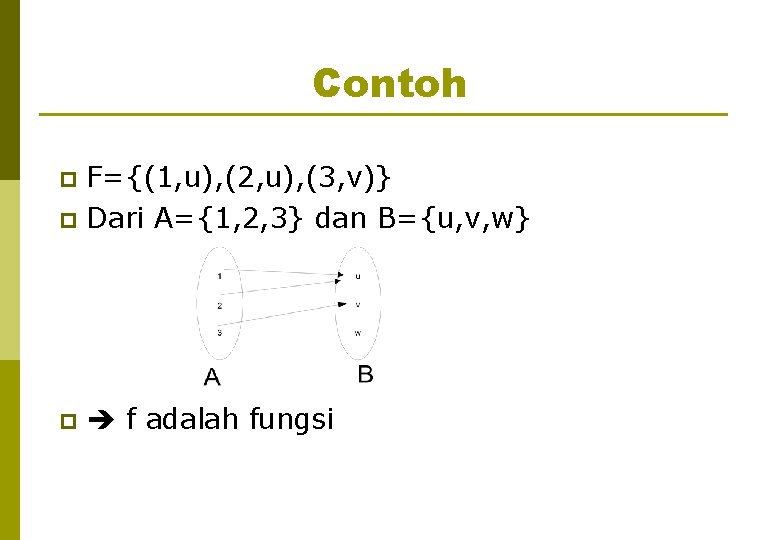
Contoh F={(1, u), (2, u), (3, v)} p Dari A={1, 2, 3} dan B={u, v, w} p p f adalah fungsi

Terminologi: p p f: A B Fungsi f memetakan (maps) A ke B A = domain dari fungsi f, B = codomain dari fungsi f f(a) = b, b disebut image (bayangan) dari a, a disebut pre-image dari b Himpunan bagian dari B yang berisi semua bayangan disebut range dari fungsi f

Contoh p Fungsi f didefinisikan sebagai f(x) = x 2 n n p A = Z = { … -2, -1, 0, 1, 2, 3, … } = domain B = Z = codomain, { 0, 1, 2, 3, … } = range Fungsi f adalah fungsi floor n n A = R = { bilangan nyata } = domain B = Z = { bilangan bulat } = codomain, range

Contoh Mencari Range p p p Let us take a look at the function f: P C with P = {Linda, Max, Kathy, Peter} C = {Boston, New York, Hong Kong, Moscow} p f(Linda) = Moscow f(Max) = Boston f(Kathy) = Hong Kong f(Peter) = New York p Here, the range of f is C. p p p

Contoh mencari range p Let us re-specify f as follows: p p f(Linda) = Moscow f(Max) = Boston f(Kathy) = Hong Kong f(Peter) = Boston p Is f still a function? yes p p What is its range? {Moscow, Boston, Hong Kong}

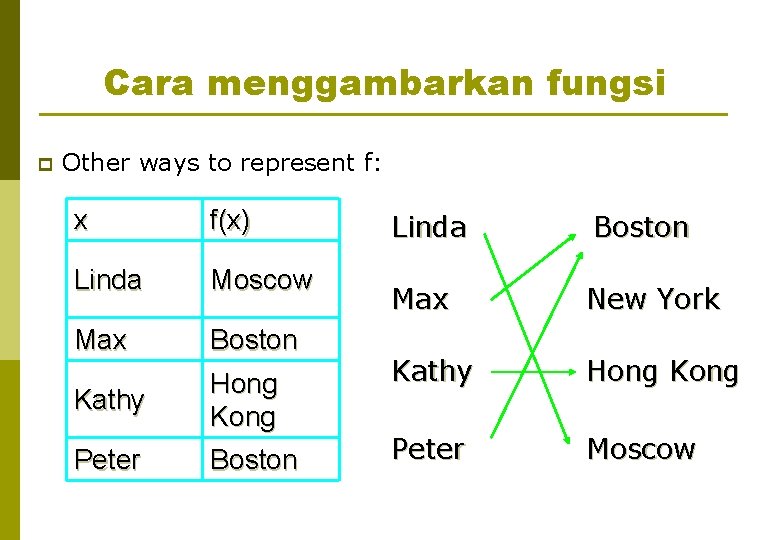
Cara menggambarkan fungsi p Other ways to represent f: x f(x) Linda Moscow Max Boston Kathy Peter Hong Kong Boston Linda Boston Max New York Kathy Hong Kong Peter Moscow

Definisi p f 1 : A R, f 2 : A R n (f 1 + f 2) (x) = f 1(x) + f 2(x) n (f 1 f 2) (x) = f 1(x) f 2(x) p f : A R n S = himpunan bagian dari A n f(S) = { f(s) | s S }

Contoh p p Contoh 1: n f 1 : R R; n f 1(x) = x 2; f 2 : R R f 2(x) = x - x 2 n (f 1 + f 2)(x) = f 1(x) + f 2(x) = (x 2) + (x - x 2) = x n (f 1 f 2)(x) = f 1(x)f 2(x) = (x 2)(x - x 2) = x 3 - x 4 Contoh 2: n n A = { a, b, c, d, e }; S = { b, c, d } B = { 1, 2, 3, 4} f(a) = 2, f(b) = 1, f(c) = 4, f(d) = 1, f(e) =1 f(S) = { 1, 4 }

Contoh p p p p p Let us look at the following well-known function: f(Linda) = Moscow f(Max) = Boston f(Kathy) = Hong Kong f(Peter) = Boston What is the image of S = {Linda, Max} ? f(S) = {Moscow, Boston} What is the image of S = {Max, Peter} ? f(S) = {Boston}

Jenis fungsi: f: A B p One-to-one, injective n Adalah element pada A mempunyai 1 pasangan pada B n f fungsi injective x y [ f(x) = f(y) x = y ] n Universe (x) = universe (y) = domain (f) = A n Contoh: p Tentukan fungsi f dari {a, b, c, d} ke {1, 2, 3, 4} dengan f(a)=4, f(b)=5, f(c)= 1, dan f(d)=3 adalah fungsi one-to-one ? a 1 b 2 c 3 d 4 5

Jenis fungsi: f: A B p Onto, surjective n Adalah semua element pada B ada pasangannya, tidak masalah jika ada cabang pada B n f fungsi surjective y x [ f(x) = y ] n Universe (x) = domain = A; universe (y) = codomain (f) = B a 1 b 2 c 3 d

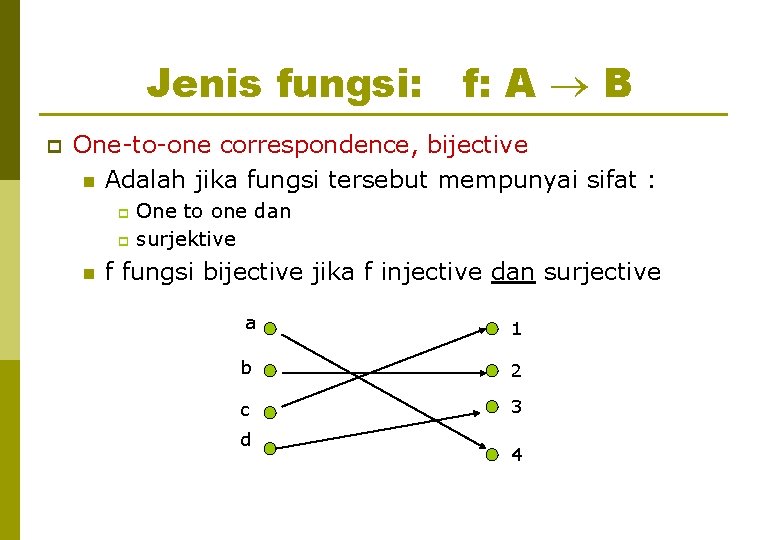
Jenis fungsi: f: A B p One-to-one correspondence, bijective n Adalah jika fungsi tersebut mempunyai sifat : One to one dan p surjektive p n f fungsi bijective jika f injective dan surjective a 1 b 2 c 3 d 4

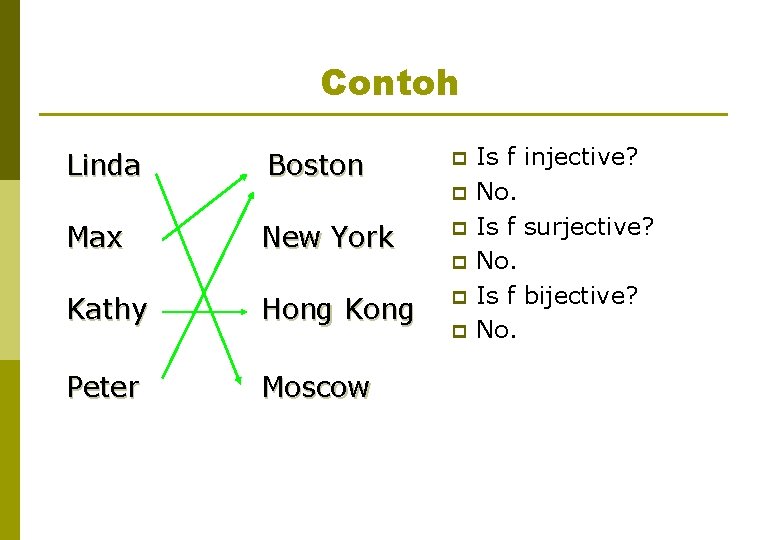
Contoh Linda Boston p p New York p Kathy Hong Kong p Peter Moscow Max p p Is f injective? No. Is f surjective? No. Is f bijective? No.

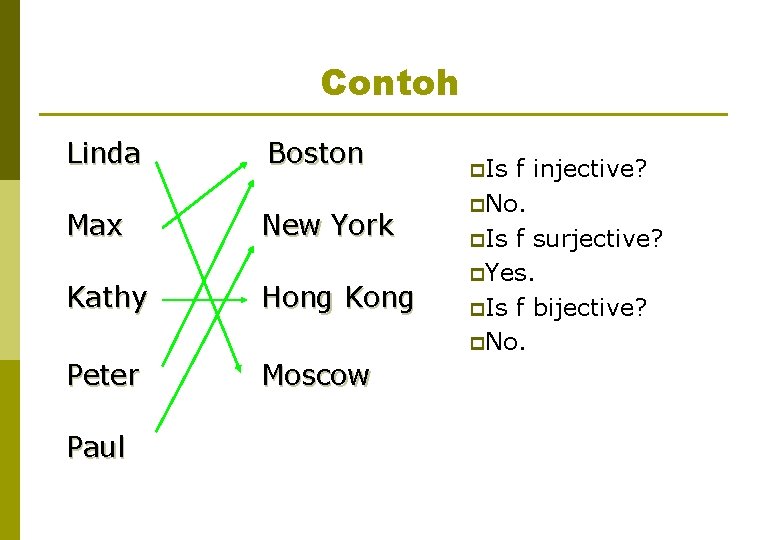
Contoh Linda Boston Max New York Kathy Hong Kong Peter Moscow Paul p. Is f injective? p. No. p. Is f surjective? p. Yes. p. Is f bijective? p. No.

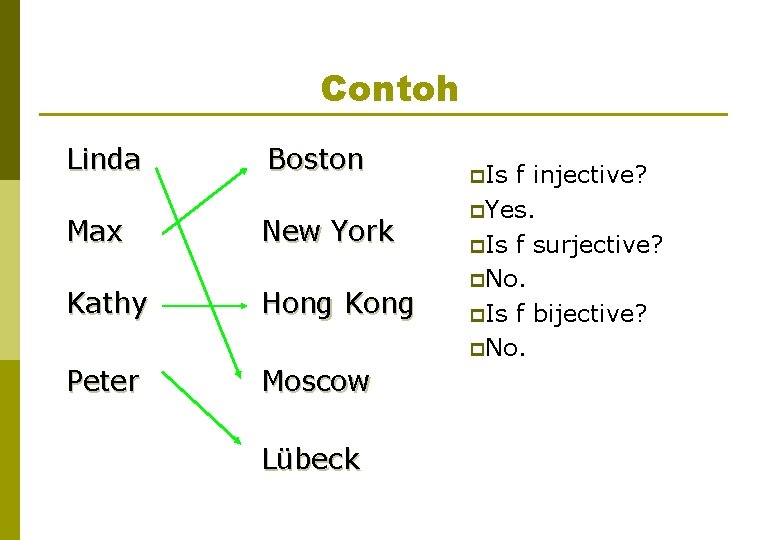
Contoh Linda Boston Max New York Kathy Hong Kong Peter Moscow Lübeck p. Is f injective? p. Yes. p. Is f surjective? p. No. p. Is f bijective? p. No.

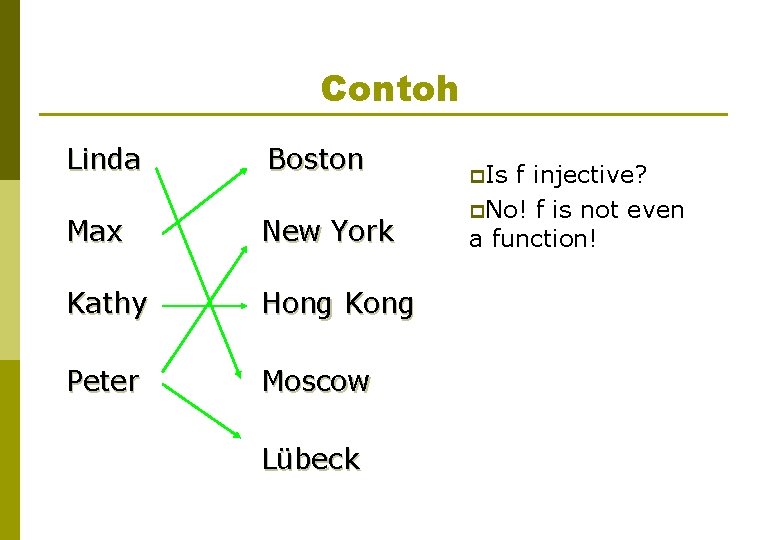
Contoh Linda Boston Max New York Kathy Hong Kong Peter Moscow Lübeck p. Is f injective? p. No! f is not even a function!

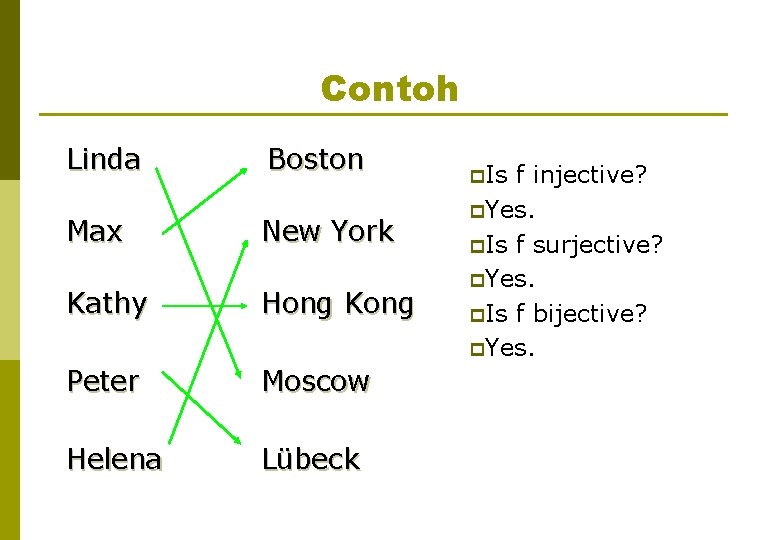
Contoh Linda Boston Max New York Kathy Hong Kong Peter Moscow Helena Lübeck p. Is f injective? p. Yes. p. Is f surjective? p. Yes. p. Is f bijective? p. Yes.

Jenis fungsi: f: A B p Strictly increasing n n p Strictly decreasing n n p x y [ ( x y ) ( f(x) f(y) ) ] Universe (x) = universe (y) = domain (f) = A Fungsi identitas f : A A n f(x) = x

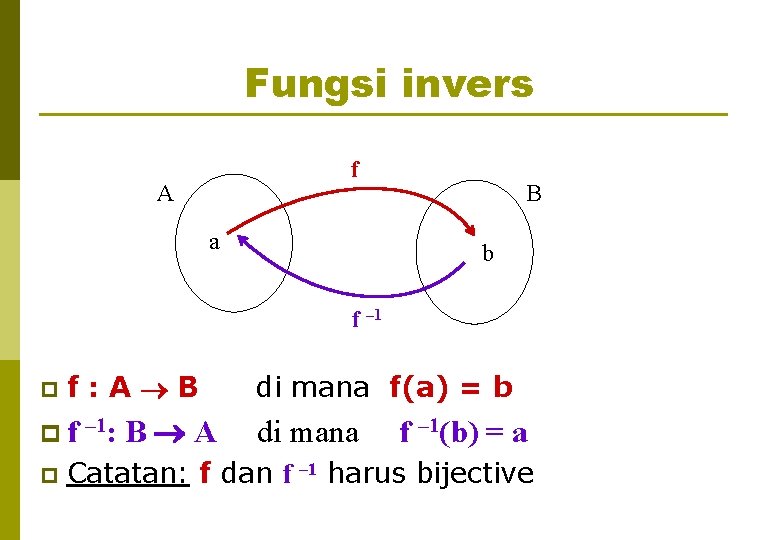
Fungsi invers f A a B b f – 1 p f: A B p f – 1: p B A di mana f(a) = b di mana f – 1(b) = a Catatan: f dan f – 1 harus bijective

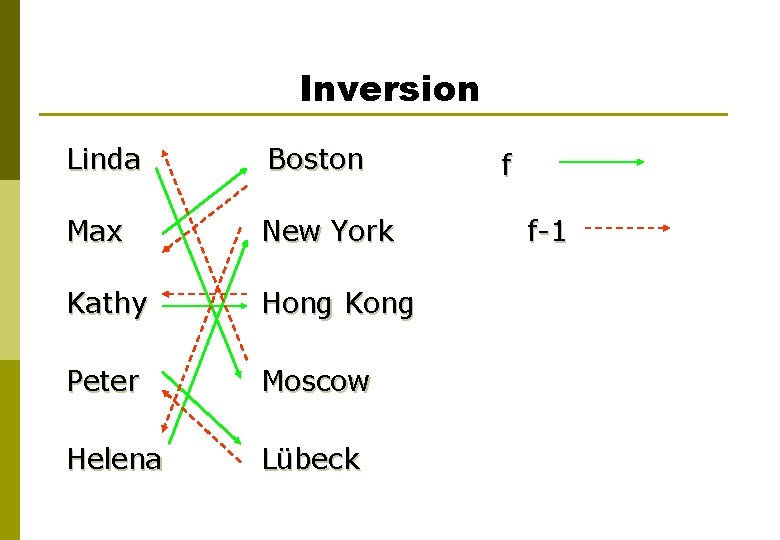
Inversion Linda Boston Max New York Kathy Hong Kong Peter Moscow Helena Lübeck f f-1

Inversion Example: The inverse function f-1 is given by: f(Linda) = Moscow f-1(Moscow) = Linda f(Max) = Boston f-1(Boston) = Max f(Kathy) = Hong Kong f-1(Hong Kong) = Kathy f(Peter) = Lübeck f-1(Lübeck) = Peter f(Helena) = New York f-1(New York) = Helena Clearly, f is bijective. Inversion is only possible for bijections (= invertible functions)

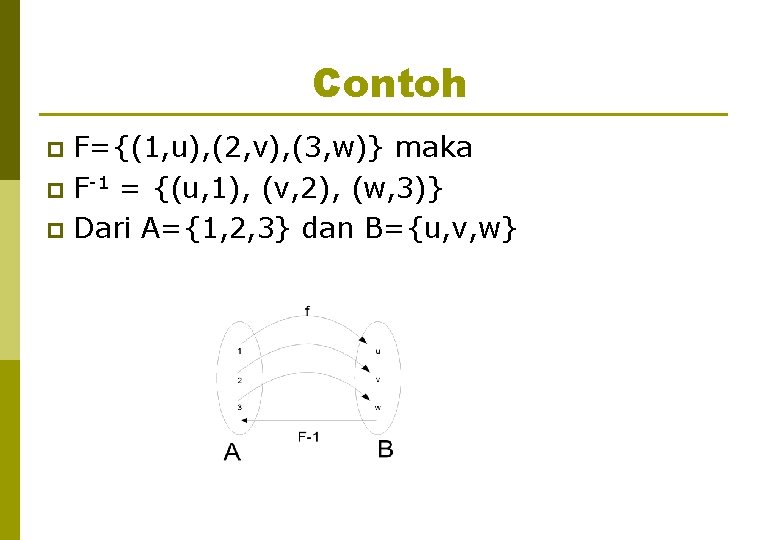
Contoh F={(1, u), (2, v), (3, w)} maka p F-1 = {(u, 1), (v, 2), (w, 3)} p Dari A={1, 2, 3} dan B={u, v, w} p

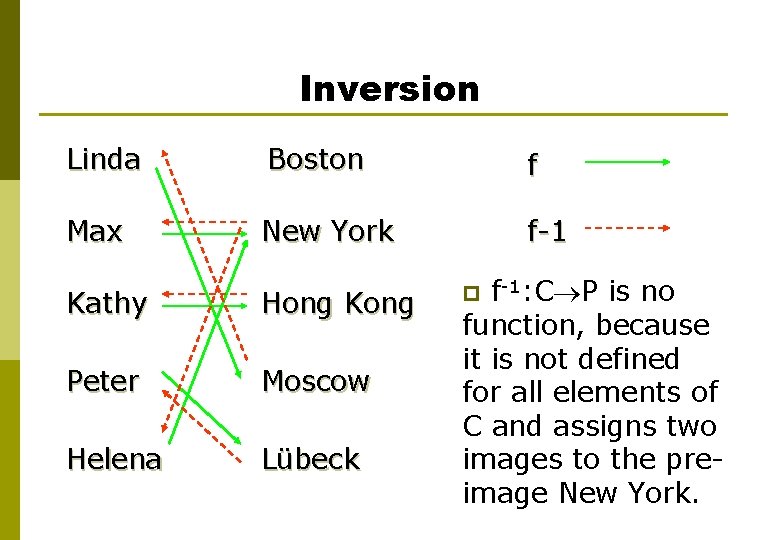
Inversion Linda Boston f Max New York f-1 Kathy Hong Kong Peter Moscow Helena Lübeck p f-1: C P is no function, because it is not defined for all elements of C and assigns two images to the preimage New York.

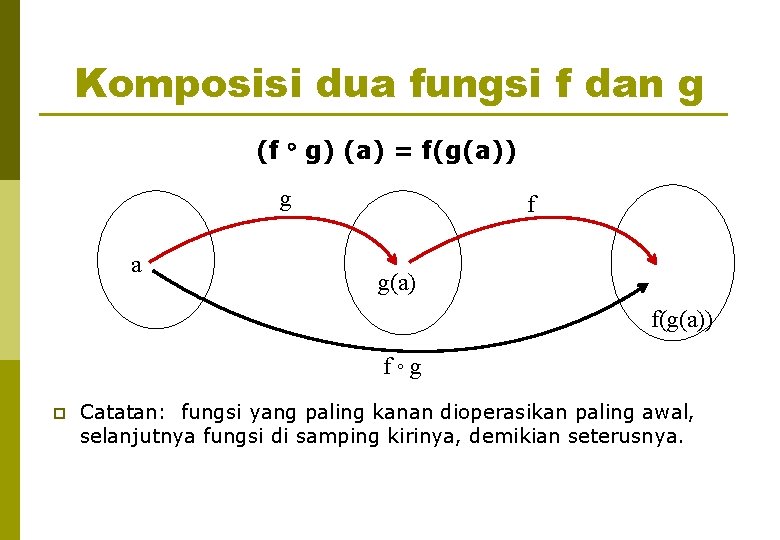
Komposisi dua fungsi f dan g (f g) (a) = f(g(a)) g a f g(a) f(g(a)) f g p Catatan: fungsi yang paling kanan dioperasikan paling awal, selanjutnya fungsi di samping kirinya, demikian seterusnya.

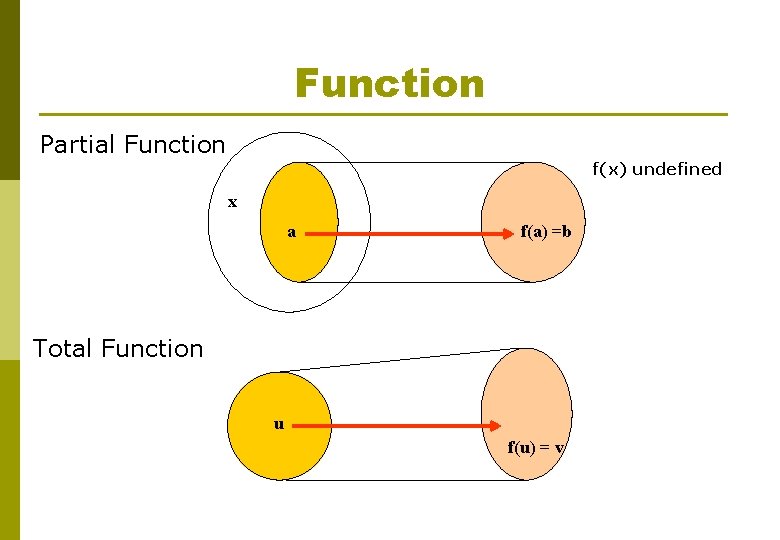
Function Partial Function f(x) undefined x a f(a) =b Total Function u f(u) = v

Tugas