Fungsi Parametrik Contoh Aplikasi MATA KULIAH BERSAMA FMIPA

+ Fungsi Parametrik Contoh & Aplikasi MATA KULIAH BERSAMA FMIPA UGM MATEMATIKA KONTEKSTUAL PERTEMUAN KE-12 Oleh : KBK MATEMATIKA TERAPAN

+ Fungsi Parameter n Definisi: Jika x dan y adalah fungsi dari t pada suatu interval I=[a, b] maka himpunan titik-titik yang didefinisikan oleh persamaan ini disebut KURVA PARAMETRIK Fungsi yang dibentuk oleh persamaaan di atas disebut FUNGSI PARAMETRIK

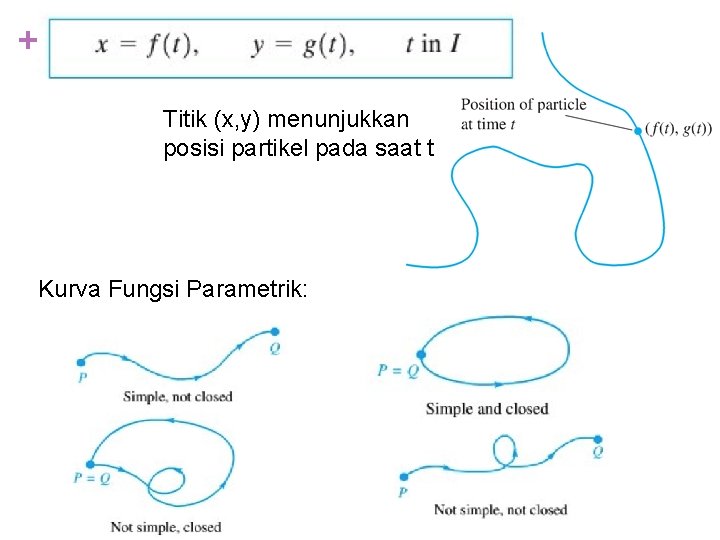
+ Titik (x, y) menunjukkan posisi partikel pada saat t Kurva Fungsi Parametrik:

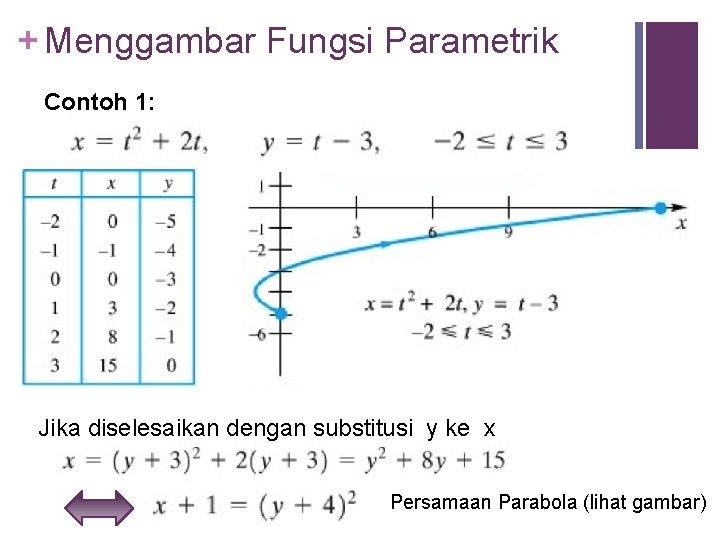
+ Menggambar Fungsi Parametrik Contoh 1: Jika diselesaikan dengan substitusi y ke x Persamaan Parabola (lihat gambar)

+ Menggambar Fungsi Parametrik Contoh 2: Persamaan parametrik diselesaikan dalam x dan y: Persamaan Elips

+ Menggambar Fungsi Parametrik Contoh 3: Ketiga fungsi parametrik di atas mengacu pada kurva yang sama: SETENGAH LINGKARAN

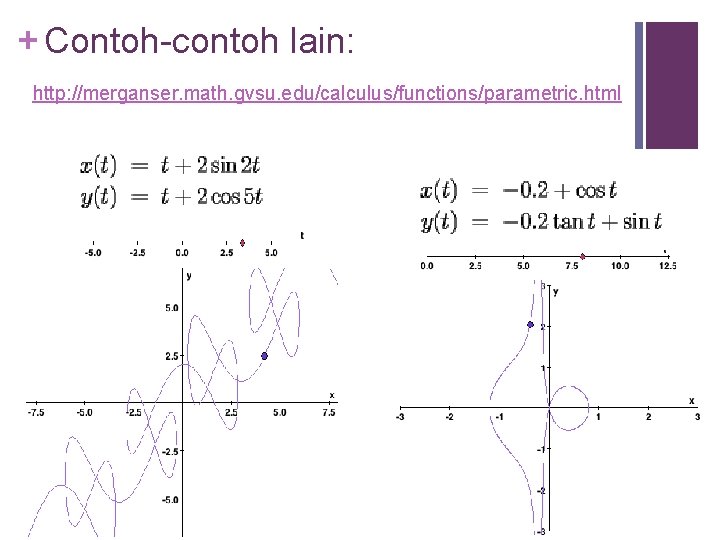
+ Contoh-contoh lain: http: //merganser. math. gvsu. edu/calculus/functions/parametric. html

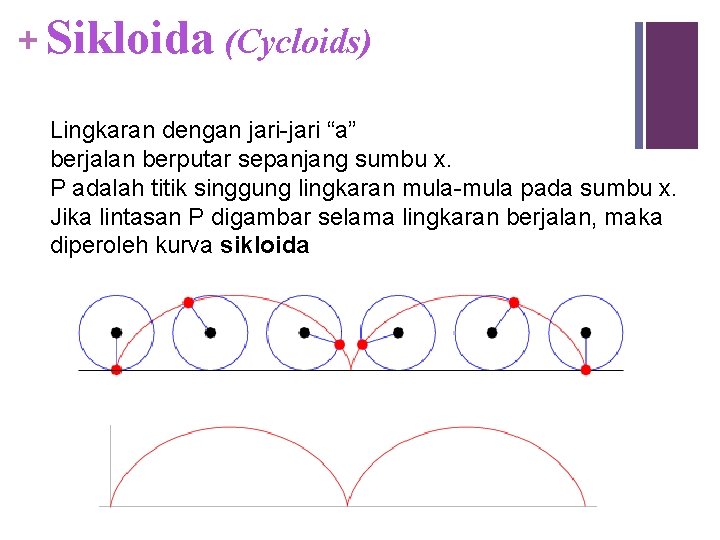
+ Sikloida (Cycloids) Lingkaran dengan jari-jari “a” berjalan berputar sepanjang sumbu x. P adalah titik singgung lingkaran mula-mula pada sumbu x. Jika lintasan P digambar selama lingkaran berjalan, maka diperoleh kurva sikloida

+ Cycloids vs Trochoids Jika titik P digeser sejauh “b” dari titik pusat lingkaran, maka lintasan titik P selama lingkaran berjalan berputar disebut trochoids Jika a=b, trochoids=cycloid. Jadi siklusoida adalah kasus khusus trokoida dengan titik P digeser sejauh a, atau sama dengan jari-jari lingkaran “a”, atau a=b. KLIK ANIMASI

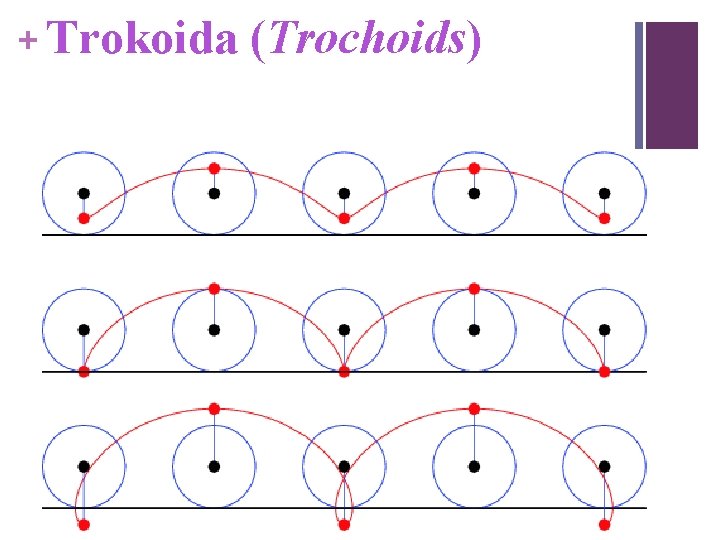
+ Trokoida (Trochoids)

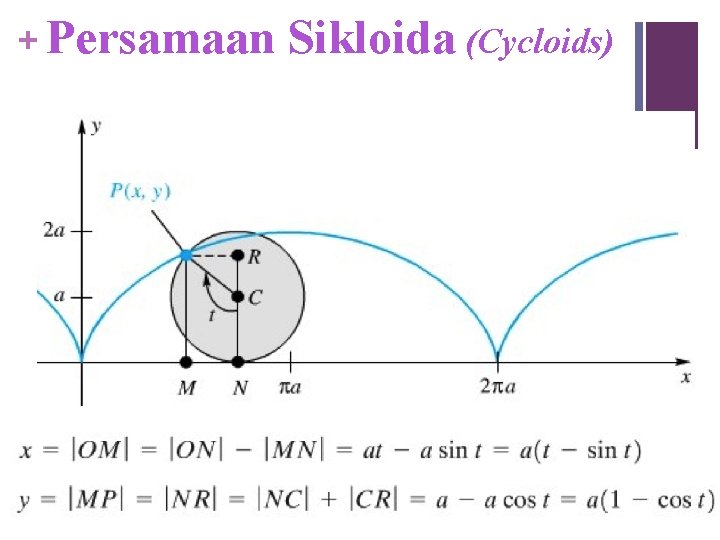
+ Persamaan Sikloida (Cycloids)

+ Rumusan Umum Cycloid

+ Visualisasi (Cycloids) Siklusoida 2π 4π 5π

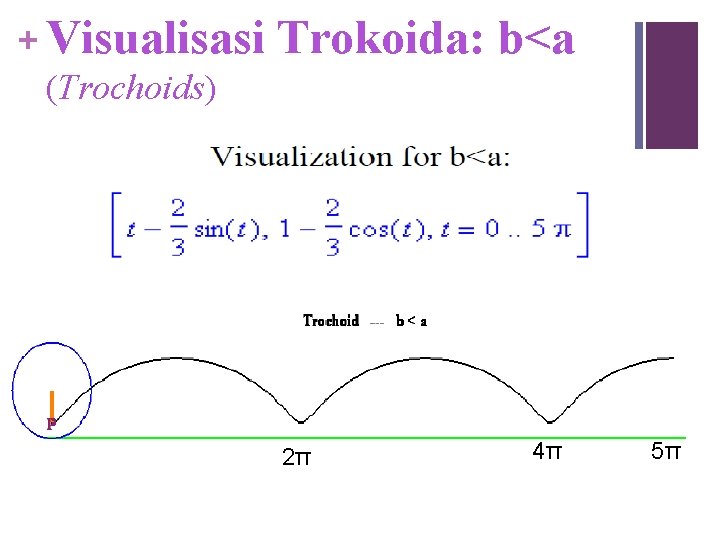
+ Visualisasi (Trochoids) Trokoida: b<a 2π 4π 5π

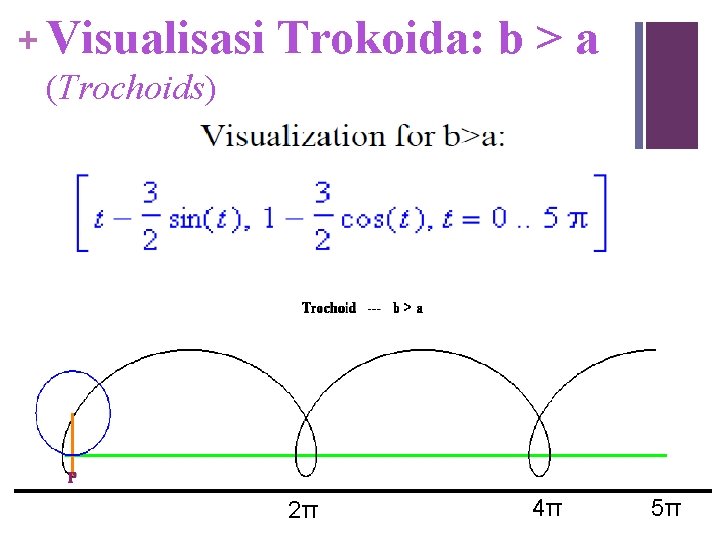
+ Visualisasi (Trochoids) Trokoida: b > a 2π 4π 5π

+ Episikloid (Epicycloids) Lingkaran B dengan jari-jari “b” bergerak sepanjang sisi luar suatu lingkaran A dengan jari-jari “a”. Lintasan titik “P” pada lingkaran B disebut EPISIKLOID

+ Episikloid (Epicycloids) Rasio “a/b” menentukan jumlah titik singgung “P” Jika “a/b = N bilangan bulat, maka terdapat N titik singgung dalam satu lintasan pada lingkaran A

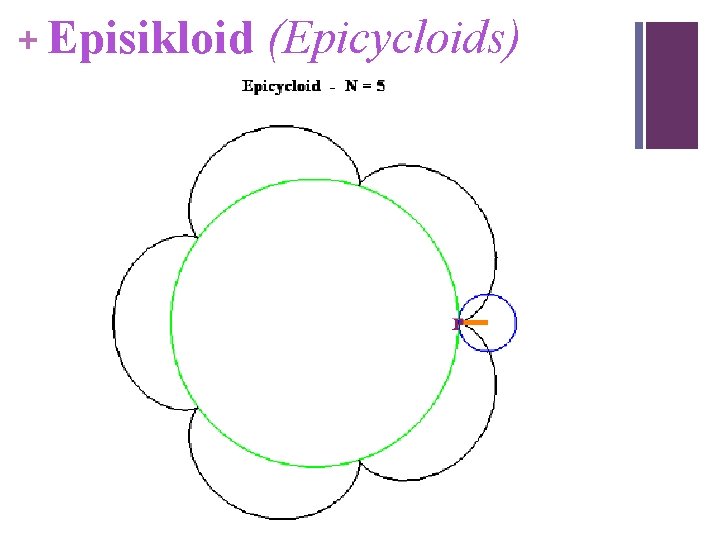
+ Episikloid (Epicycloids)

+ Rumusan Umum Epicycloid Contoh: a=1, b=1/5 Next

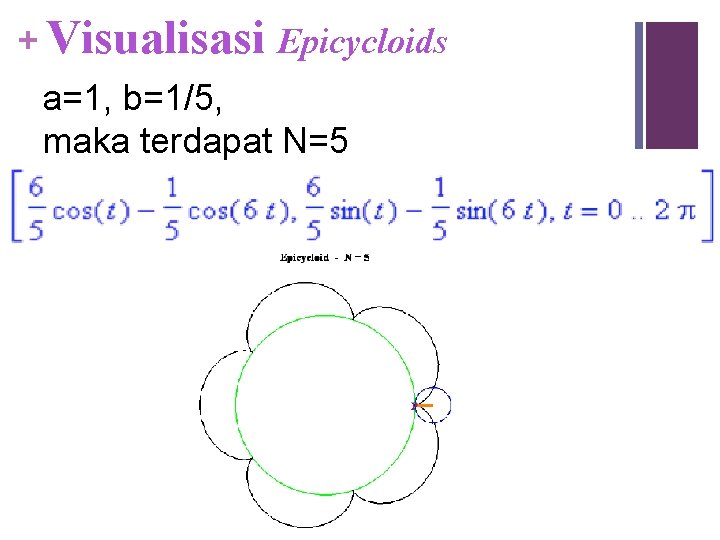
+ Visualisasi Epicycloids a=1, b=1/5, maka terdapat N=5

+ Hiposikloid (Hypocycloids) Lingkaran B dengan jari-jari “b” bergerak sepanjang sisi dalam suatu lingkaran A dengan jari-jari “a”. Lintasan titik “P” pada lingkaran B disebut HIPOSIKLOID

+ Hiposikloid (Hypocycloids) Rasio “a/b” menentukan jumlah titik singgung “P” Jika “a/b = N bilangan bulat, maka terdapat N titik singgung dalam satu lintasan pada lingkaran A

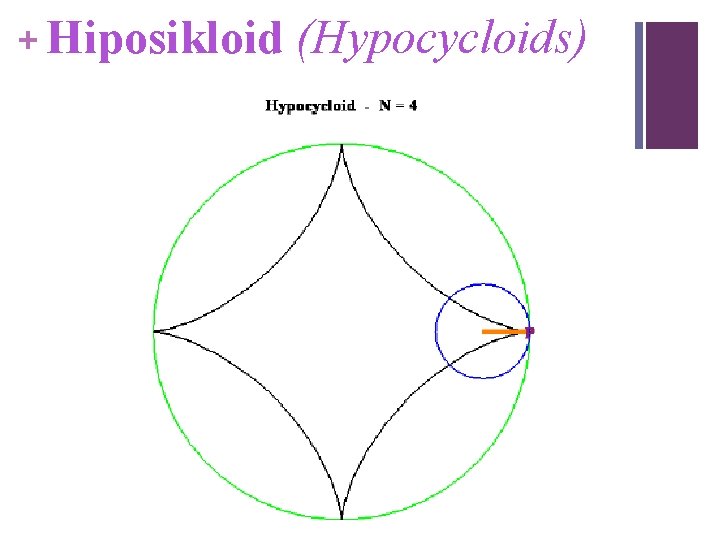
+ Hiposikloid (Hypocycloids)

+ Rumusan Umum Hypocycloid Contoh: a=1, b=1/4 Next

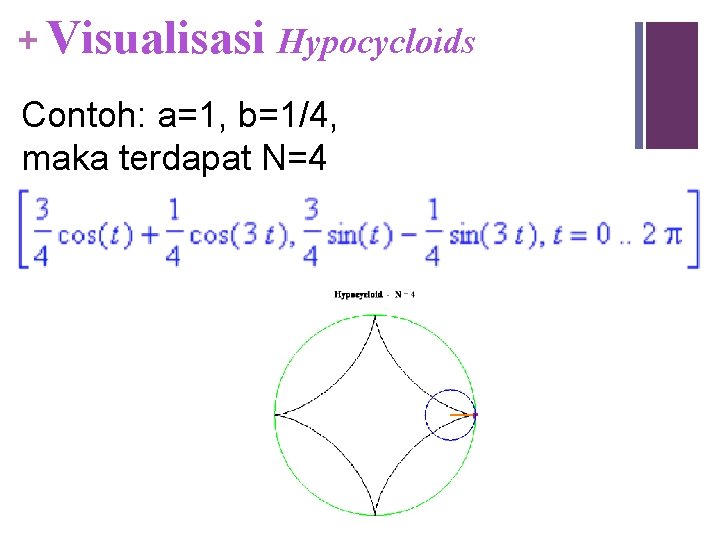
+ Visualisasi Hypocycloids Contoh: a=1, b=1/4, maka terdapat N=4

+ Epitrokoida (Epitrochoids) Lingkaran B dengan jari-jari “b” bergerak (berlawanan arah jarum jam) dengan titik pusat lingkaran B pada lingkaran A yang jari -jarinya “a”. Lintasan titik “P” pada lingkaran B disebut EPITROKOIDA. Misal lingkaran B berputar “c” kali, maka terdapat N=(c-1) titik singgung(“verteks”)

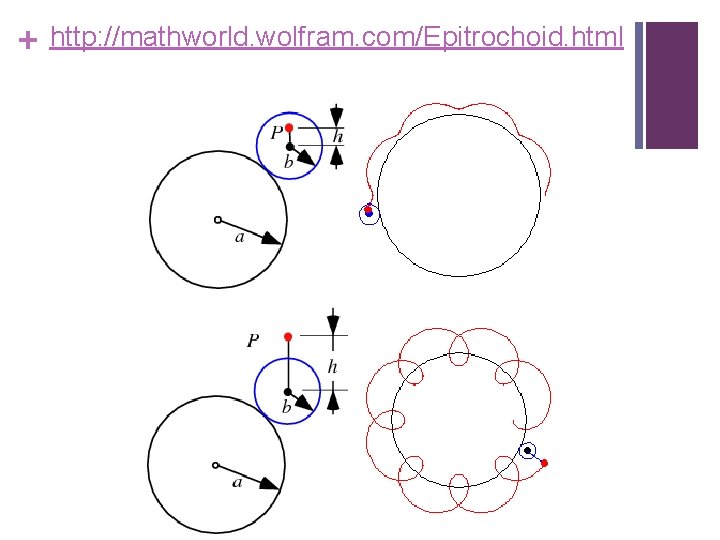
+ http: //mathworld. wolfram. com/Epitrochoid. html

+ CATATAN: Jika “a/b=c” maka kurva ini adalah EPICYCLOID, Jika “b < a/c”, maka seperti trokoida dengan b<a. Jika “b > a/c”, maka seperti trokoida dengan b>a.

+ Rumus Umum Epitrochoids Contoh: a=1 , b=1/2 Next

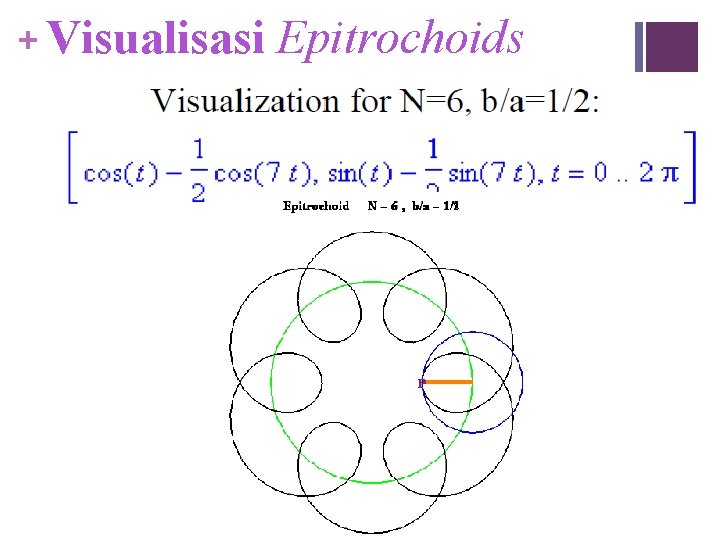
+ Visualisasi Epitrochoids

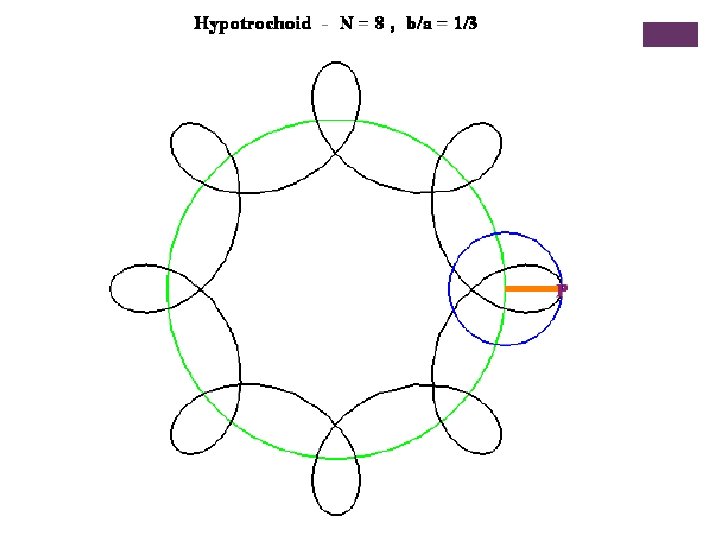
+ Hipotrokoida (Hypotrochoids) Lingkaran B dengan jari-jari “b” bergerak (searah jarum jam) dengan titik pusat lingkaran B pada lingkaran A yang jari-jarinya “a”. Lintasan titik “P” pada lingkaran B disebut HIPOTROKOIDA. Misal lingkaran B berputar “c” kali, maka terdapat N=(c+1) titik singgung(“verteks”)

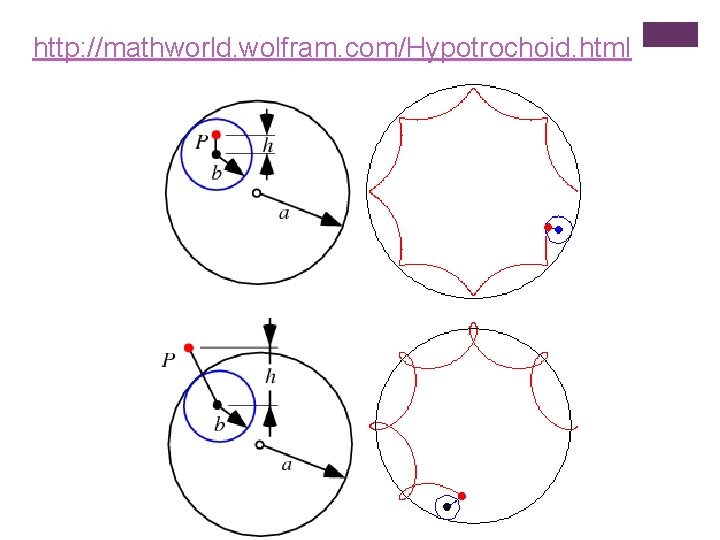
http: //mathworld. wolfram. com/Hypotrochoid. html

CATATAN: Jika “a/b=c” maka kurva ini adalah HYPOCYCLOID, Jika “b < a/c”, maka seperti trokoida dengan b<a. Jika “b > a/c”, maka seperti trokoida dengan b>a.

Rumus Umum Hypotrochoids Next

3. G. B. Thomas , M. D. Weir, J. Hass, Thomas' Calculus, Addison Wesley; 12 th edition (September 12, 2009) 4. D. Varberg, E. Purcell, S. Rigdon, Calculus, 9/E, Pearson, 2007’ 5. http: //mathworld. wolfram. com/Parametric. Equations. html END