Funes Trigonomtricas Professora Ursula Timm Conhecendo a Circunferncia

Funções Trigonométricas Professora Ursula Timm

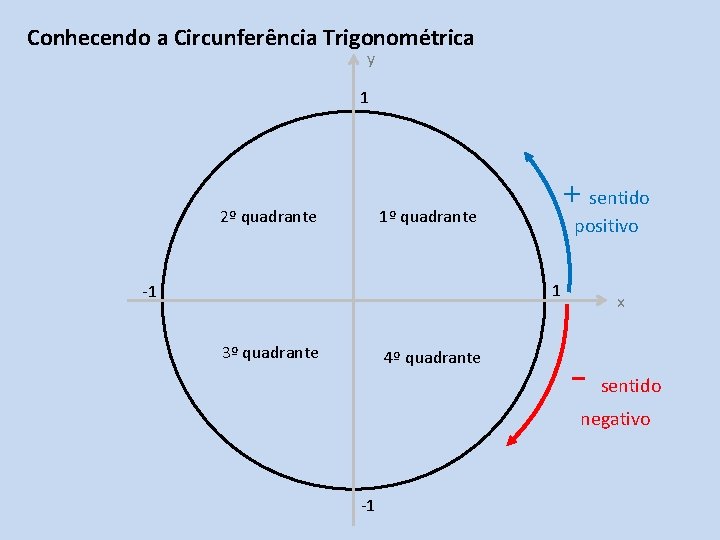
Conhecendo a Circunferência Trigonométrica y 1 2º quadrante + sentido 1º quadrante positivo 1 -1 3º quadrante 4º quadrante x - sentido negativo -1

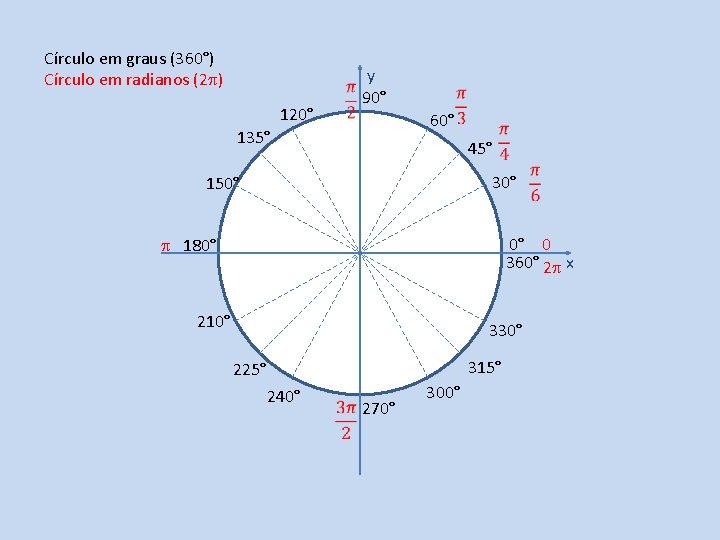
Círculo em graus (360°) Círculo em radianos (2 ) 120° y 90° 60° 135° 45° 30° 150° 180° 0° 0 360° 2 x 210° 330° 315° 225° 240° 270° 300°

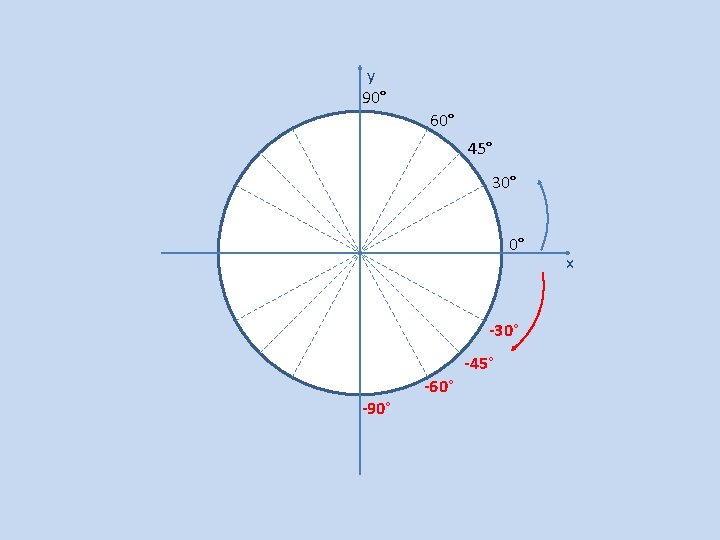
y 90° 60° 45° 30° 0° -30° -45° -60° -90° x

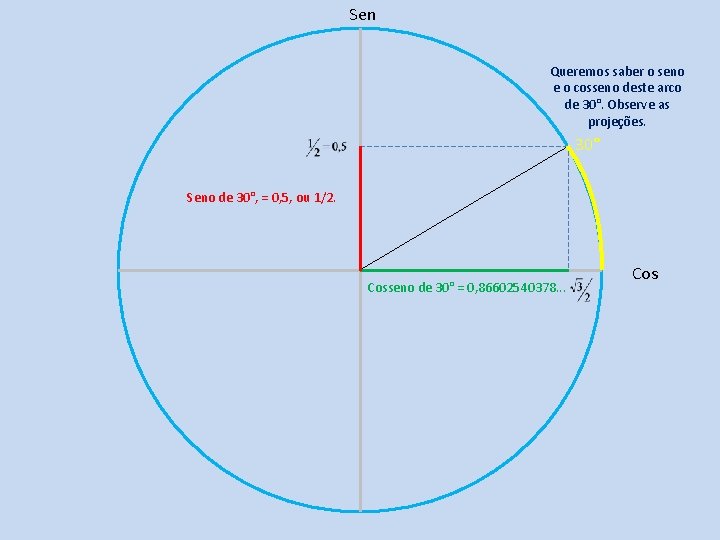
Sen Queremos saber o seno e o cosseno deste arco de 30°. Observe as projeções. 30° Seno de 30°, = 0, 5, ou 1/2. Cosseno de 30° = 0, 86602540378. . . Cos

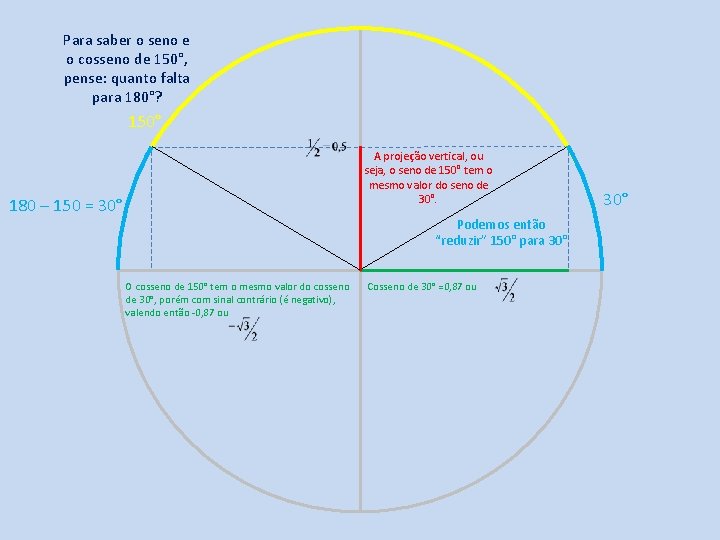
Para saber o seno e o cosseno de 150°, pense: quanto falta para 180°? 150° A projeção vertical, ou seja, o seno de 150° tem o mesmo valor do seno de 30°. 180 – 150 = 30° Podemos então “reduzir” 150° para 30° O cosseno de 150° tem o mesmo valor do cosseno de 30°, porém com sinal contrário (é negativo), valendo então -0, 87 ou Cosseno de 30° =0, 87 ou 30°

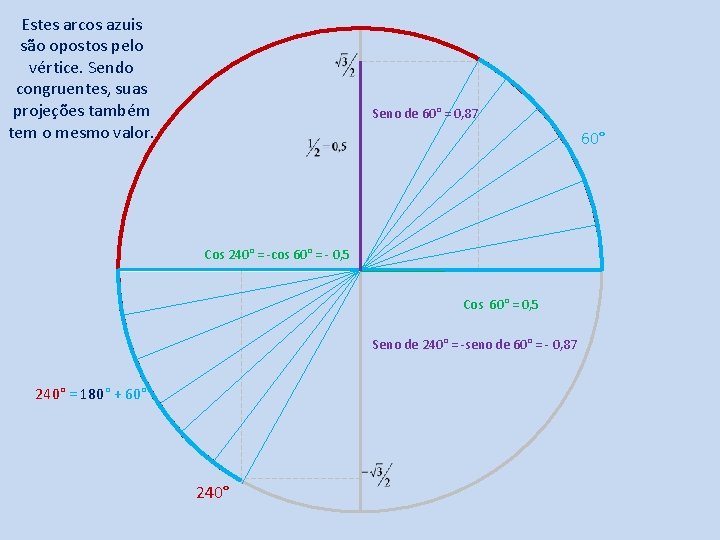
Estes arcos azuis são opostos pelo vértice. Sendo congruentes, suas projeções também tem o mesmo valor. Seno de 60° = 0, 87 60° Cos 240° = -cos 60° = - 0, 5 Cos 60° = 0, 5 Seno de 240° = -seno de 60° = - 0, 87 240° = 180° + 60° 240°

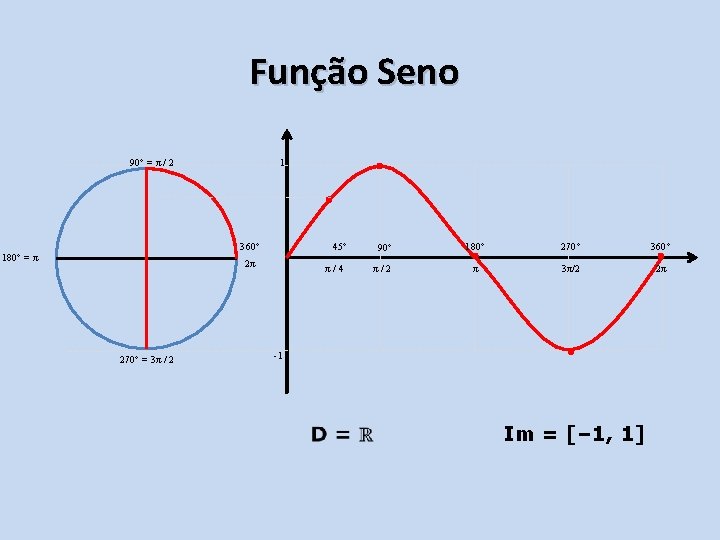
Função Seno 90° = π / 2 1 360° 180° = π 45° 2π 270° = 3π / 2 π/4 90° 180° 270° 360° π/2 π 3π/2 2π -1 Im = [– 1, 1]

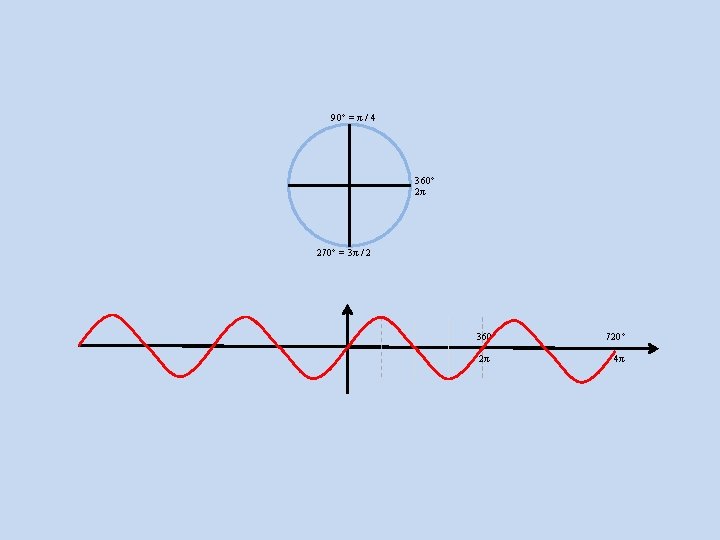
90° = π / 4 360° 2π 270° = 3π / 2 360° 720° 2π 4π

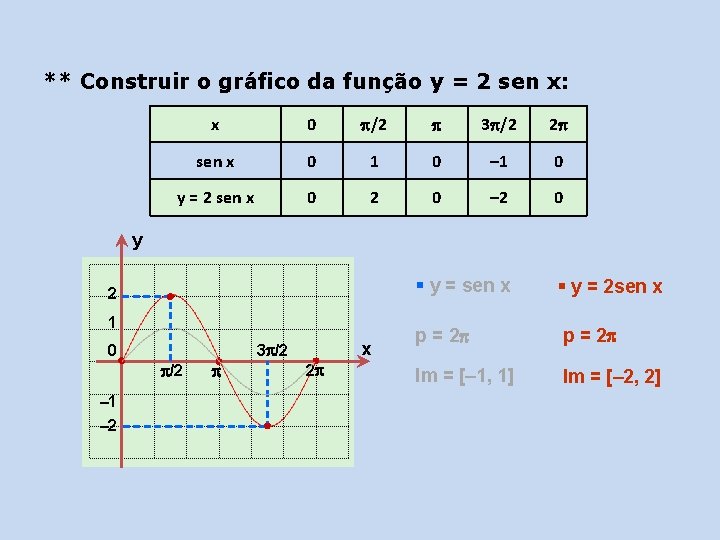
** Construir o gráfico da função y = 2 sen x: x 0 /2 3 /2 2 sen x 0 1 0 – 1 0 y = 2 sen x 0 2 0 – 2 0 y 2 1 0 /2 – 1 – 2 x 3 /2 2 § y = sen x § y = 2 sen x p = 2 Im = [– 1, 1] Im = [– 2, 2]

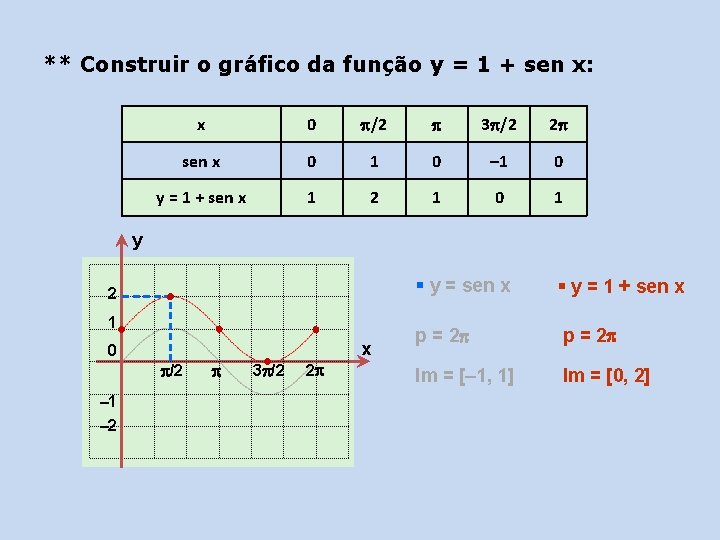
** Construir o gráfico da função y = 1 + sen x: x 0 /2 3 /2 2 sen x 0 1 0 – 1 0 y = 1 + sen x 1 2 1 0 1 y 2 1 x 0 /2 – 1 – 2 3 /2 2 § y = sen x § y = 1 + sen x p = 2 Im = [– 1, 1] Im = [0, 2]

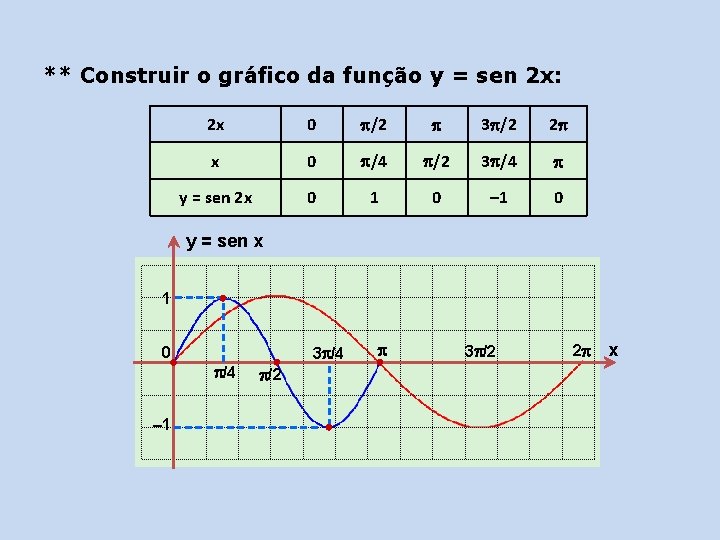
** Construir o gráfico da função y = sen 2 x: 2 x 0 /2 3 /2 2 x 0 /4 /2 3 /4 y = sen 2 x 0 1 0 – 1 0 y = sen x 1 0 /4 – 1 3 /4 /2 3 /2 2 x

Função cosseno y /2 1 0 /2 -1 3 /2 2 Im=[-1, 1] P = 2 3 /2 2 x

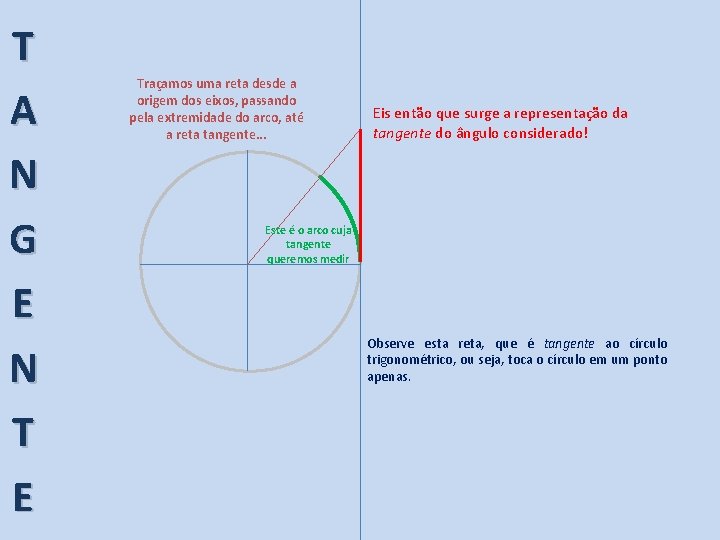
T A N G E N T E Traçamos uma reta desde a origem dos eixos, passando pela extremidade do arco, até a reta tangente. . . Eis então que surge a representação da tangente do ângulo considerado! Este é o arco cuja tangente queremos medir Observe esta reta, que é tangente ao círculo trigonométrico, ou seja, toca o círculo em um ponto apenas.

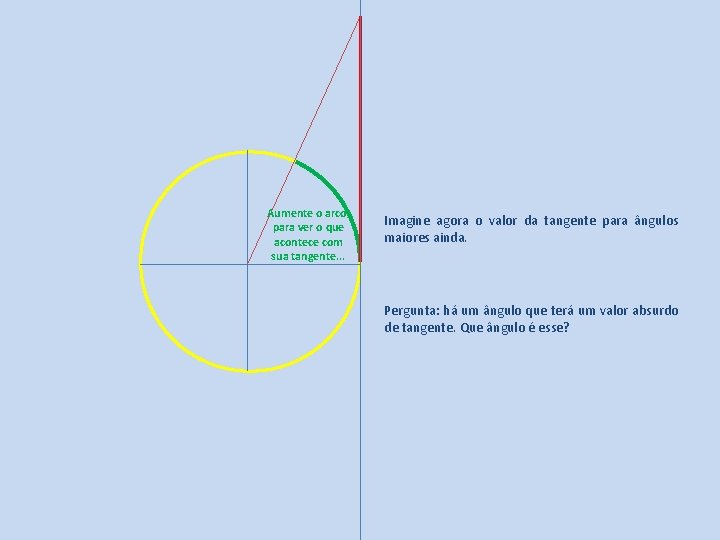
Aumente o arco, para ver o que acontece com sua tangente. . . Imagine agora o valor da tangente para ângulos maiores ainda. Pergunta: há um ângulo que terá um valor absurdo de tangente. Que ângulo é esse?

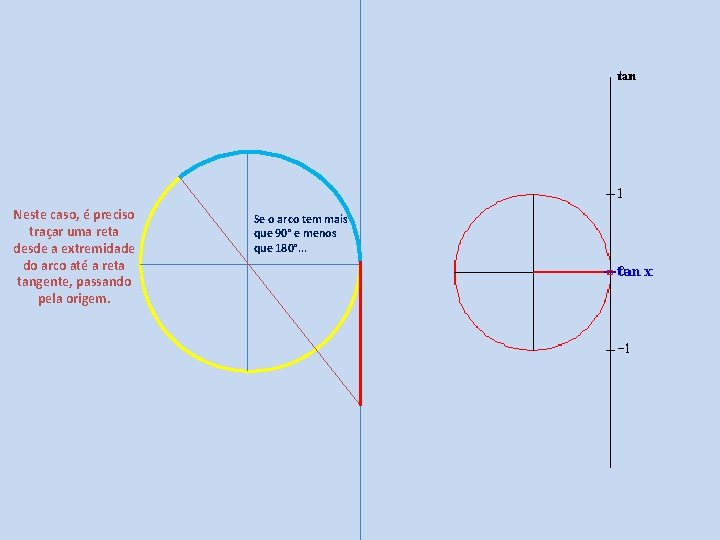
Neste caso, é preciso traçar uma reta desde a extremidade do arco até a reta tangente, passando pela origem. Se o arco tem mais que 90° e menos que 180°. . .

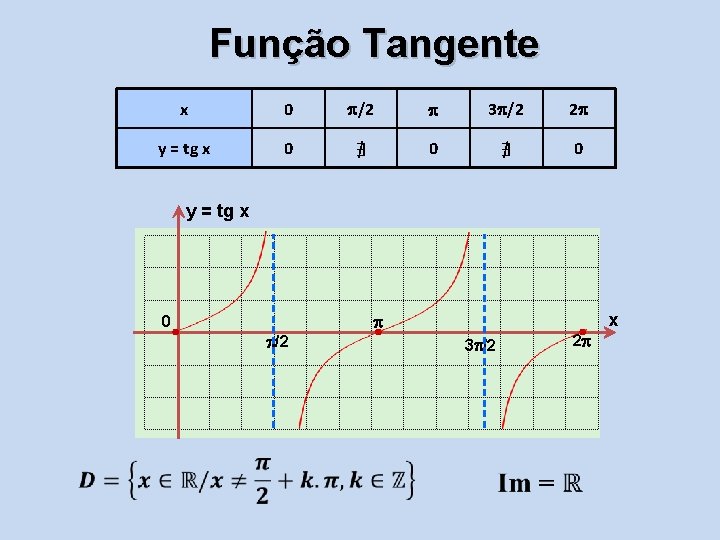
Função Tangente x 0 /2 3 /2 2 y = tg x 0 ∄ 0 y = tg x x 0 /2 3 /2 2

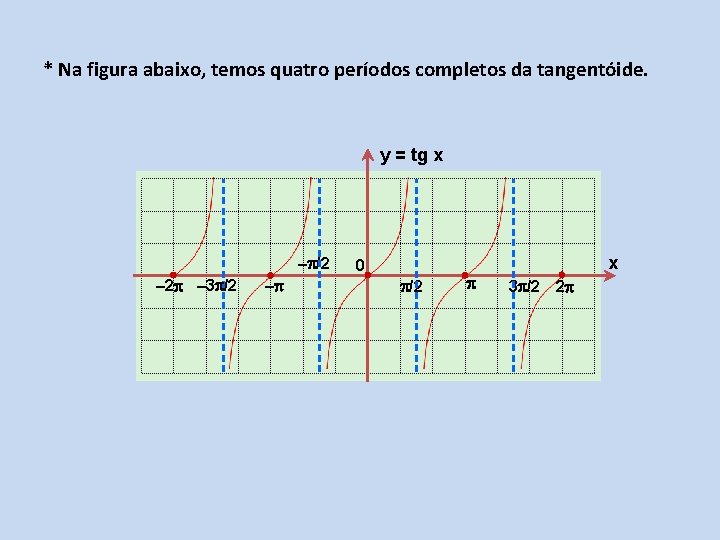
* Na figura abaixo, temos quatro períodos completos da tangentóide. y = tg x – /2 – 3 /2 – 0 /2 x 3 /2 2

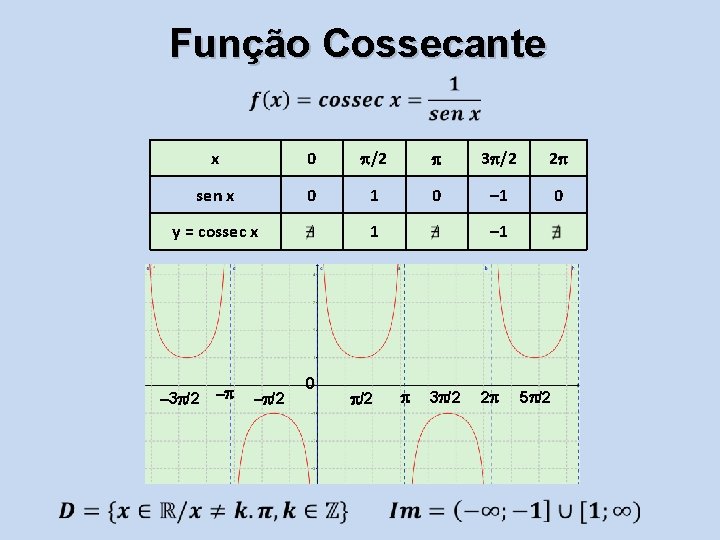
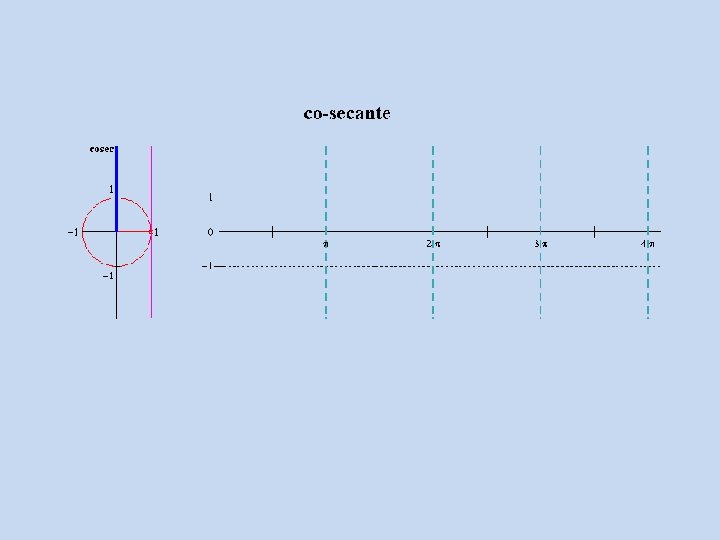
Função Cossecante x 0 /2 3 /2 2 sen x 0 1 0 – 1 0 y = cossec x – 3 /2 – – /2 1 0 /2 – 1 3 /2 2 5 /2

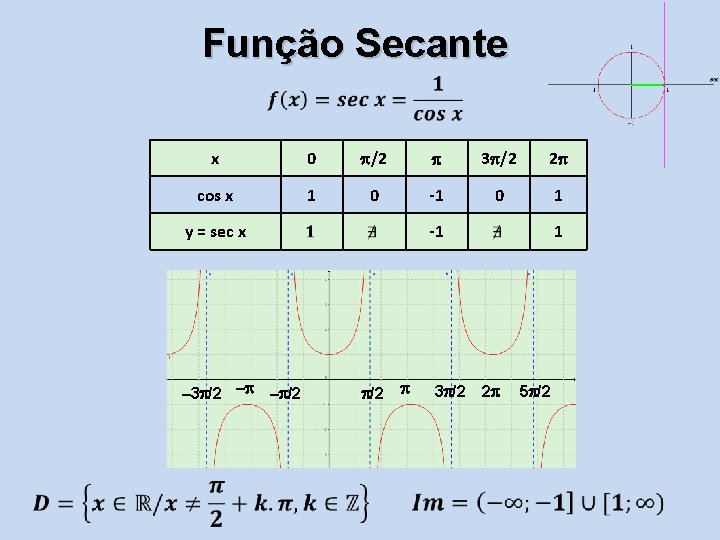
Função Secante x 0 /2 3 /2 2 cos x 1 0 -1 0 1 y = sec x – 3 /2 – -1 – /2 3 /2 1 2 5 /2

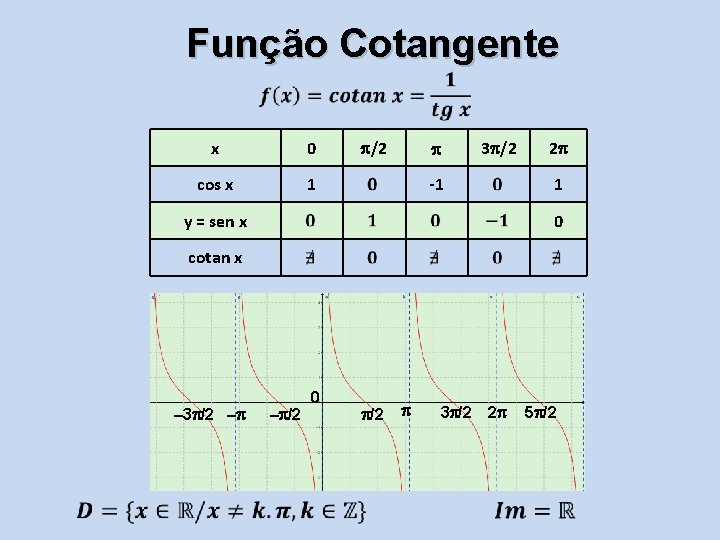
Função Cotangente x 0 cos x 1 /2 3 /2 -1 2 1 y = sen x 0 cotan x – 3 /2 – – /2 0 /2 3 /2 2 5 /2