Funes logartmicas Funes logartmicas n De modo geral

Funções logarítmicas

Funções logarítmicas n De modo geral, se a é uma constante real (a > 0 e a ≠ 1), chamamos de função logaritmo de base a a função definida por: y = f(x) = loga x É claro que x > 0.

Exemplos n y = log 5 x → 5 é a função logaritmo de base n y = log x → é a função logaritmo de base 10 n y = log 1/2 x → é a função logaritmo de base 1/2 O gráfico de uma função logarítmica é uma curva chamada de curva logarítmica.

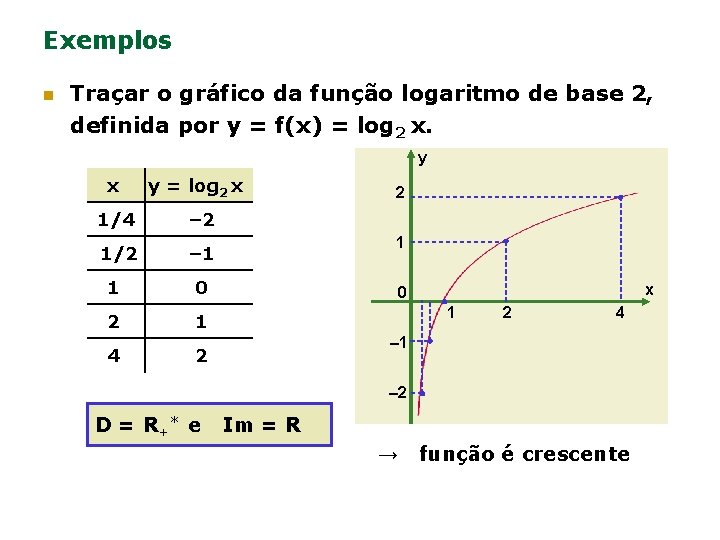
Exemplos n Traçar o gráfico da função logaritmo de base 2, definida por y = f(x) = log 2 x. y x y = log 2 x 1/4 – 2 1/2 – 1 1 0 2 1 4 2 2 1 x 0 1 2 4 – 1 – 2 D = R+ * e Im = R → função é crescente

Exemplos n Traçar o gráfico da função logaritmo de base 1/2, definida por y = f(x) = log 1/2 x. y x y = log 1/2 x 1/4 2 1/2 1 1 0 2 – 1 4 – 2 D = R+ * e 2 1 0 1 2 4 x – 1 Im = R – 2 → função é decrescente

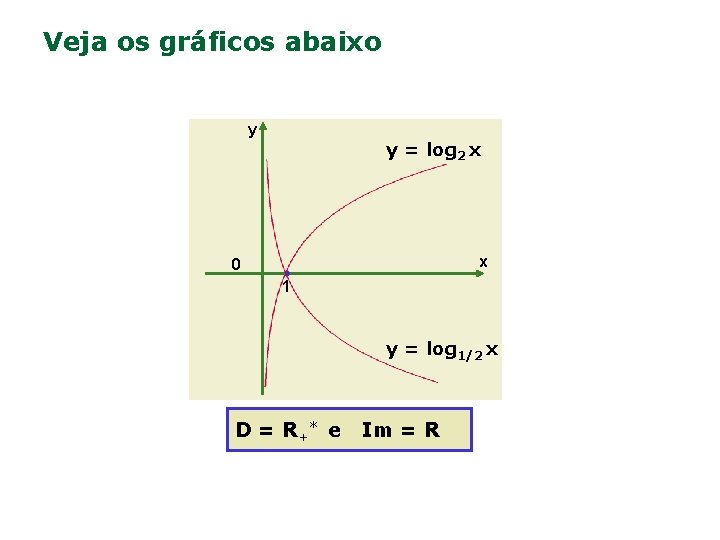
Funções logaritmos - Resumo n Da análise dos dois últimos gráficos, tiramos algumas conclusões sobre a função logaritmo y = loga x (a > 0 e a ≠ 1): ü O domínio é os Reais positivos (x > 0); ü O conjunto imagem é os Reais; ü Ela é crescente em todo o seu domínio para a > 1. ü Ela é decrescente em todo o seu domínio para 0 < a < 1.

Veja os gráficos abaixo y y = log 2 x x 0 1 y = log 1/2 x D = R+ * e Im = R

Propriedades da função logaritmo

Propriedades operatórias n A função logaritmo y = loga x é sempre crescente ou sempre decrescente. Isso significa que logaritmos numa mesma base só são iguais para logaritmandos iguais. loga m = loga n ⇔ m = n

Exemplos n log 3 x = log 3 5 ⇔ x=5 n log (3 x – 1) = log 2 x ⇔ 3 x – 1 = 2 x ⇒ x=1

Observação n A propriedade que acabamos de demonstrar pode ser interpretada no sentido inverso. Se dois números são iguais, então seus logaritmos numa mesma base são iguais. m=n ⇒ loga m = loga n

Exemplos n Resolver a equação exponencial 4 x = 3 x+1, a partir dos valores log 2 = 0, 301 e log 3 = 0, 477. 4 x = 3 x+1 ⇒ log 4 x = log 3 x+1 ⇒ x. log 4 = (x + 1). log 3 ⇒ x. (2. log 2) = (x + 1). log 3 ⇒ x. (2. 0, 301) = (x + 1). 0, 477 ⇒ 0, 602. x = 0, 477. x + 0, 477 ⇒ 0, 125. x = 0, 477 ⇒ x = 3, 816

Propriedades operatórias n A função logaritmo y = loga x é crescente em todo o seu domínio, se a > 1. y ü Quanto maior o valor de x maior é o valor de loga x. loga m loga n x 0 n m loga m > longa n ⇔ m > n Mesmo sentido

Propriedades operatórias n A função logaritmo y = loga x é decrescente em todo o seu domínio, se 0 < a < 1. y ü Quanto maior o valor de x menor é o valor de loga x. 0 n m x loga n loga m < loga n ⇔ m > n Sentidos contrários

Exemplos n log x < log 3 ⇒ x<3 base > 1, sinal mantido n log 2/5 (x – 3) < log 2/5 4 ⇒ x– 3>4 ⇒ 0 < a < 1, sinal invertido x>7

Equações e inequações logarítmicas

Equações e inequações logarítmicas n n Em certas equações e inequações que envolvem logaritmo, a variável aparece no logaritmando. A resolução de uma equação e uma inequação logarítmica se baseia nas propriedades abaixo. P 1. loga m = loga n ⇔ m = n P 2. loga m > loga n ⇔ m > n (a > 1) P 3. loga m < loga n ⇔ m > n (0 < a < 1)

Exemplos n Resolver a equação 2 log 2 x = 1 + log 2 (x + 12). Condição de existência x>0 x + 12 > 0 ⇒ x>0 2 log 2 x = log 2 2 + log 2 (x + 12) ⇒ log 2 x 2 = log 2 2(x + 12) ⇒ log 2 x 2 = log 2 (2 x + 24) ⇒ x 2 = 2 x + 24 ⇒ x 2 – 2 x – 24 = 0 ⇒ x’ = – 4 ou x” = 6 S = {6}.

Exemplos n Resolver a inequação log (x – 1) ≥ log (5 – x). x– 1>0 Condição de existência 1<x<5 5–x>0 ⇒ x>1 x<5 (1) log (x – 1) ≥ log (5 – x) ⇒ 2 x ≥ 6 ⇒ x ≥ 3 ⇒ x– 1≥ 5–x (2) Fazendo a interseção das condições, (1) e (2), temos S = 3 ≤ x < 5.

Exemplos n Obter o domínio da função definida por y= 1 √log 1/3 x + 2 O radicando deve ser maior que zero, logo log 1/3 x + 2 > 0 ⇒ log 1/3 x > – 2 ⇒ log 1/3 x > log 1/3 9 ⇒ x < 9 S = {0 < x < 9}.

Aplicando logaritmos em problemas de crescimento e decrescimento

Aplicação dos logaritmos n As funções exponenciais aparecem nas situações em que uma variável cresce ou decresce com o tempo, segundo uma taxa fixa. n Nesses casos, os logaritmos são muito úteis quando se necessário pretende para que determinado valor. descobrir aquela o variável tempo atinja

Exemplos n Giovanna aplicou R$ 1 000, 00 a juros compostos a uma taxa de 5% ao mês. Após quanto tempo ela obteve R$ 500, 00 de juros? M = C. (1 + i)t ⇒ ⇒ 1, 05 t = 1, 5 ⇒ 1 500 = 1 000. (1, 05)t log 1, 05 t = log 1, 5 ⇒ t. log 1, 05 = log 1, 5 ⇒ t = log 1, 5 log 1, 05 ⇒ t = 0, 1761 0, 0210 ⇒ t = 8, 39 ⇒ t ≈ 9 meses

Exemplos n Giovanna aplicou R$ 1 000, 00 a juros compostos a uma taxa de 5% ao mês. Após quanto tempo ela obteve R$ 500, 00 de juros? Dados: log 3 = 0, 477, log 5 = 0, 699 e log 7 = 0, 845. log 1, 5 =log (15/10) = log 15 – log 10 Chegamos à equação: = log 1, 5 t. log = log 1, 05 3 + log 5 – 1, 5 log 10 log 1, 5 = 0, 477 + 0, 699 – 1 = 0, 176 ⇒ t = log 1, 5 log 1, 05 = 0, 176 0, 021 ⇒ t = 8, 39 log 1, 05 =log (105/100) = log 105 – log 100 log 1, 05 = log 3 + log 5 + log 7 – log 100 log 1, 05 = 0, 477 + 0, 699 + 0, 845 – 2 = 0, 021

Exemplos n Um determinado automóvel desvaloriza-se segundo uma taxa composta, equivalente a 5% ao ano. Daqui a quanto tempo ele valerá 80% do que vale hoje? ⇒ 0, 8 V 0 = V 0. (0, 95)t ⇒ 0, 95 t = 0, 8 ⇒ log 0, 95 t = log 0, 8 M = C. (1 + i)t ⇒ t. log 0, 95 = log 0, 8 ⇒ t = log 0, 8 log 0, 95 ⇒ t = – 0, 0969 – 0, 0223 ⇒ t = 4, 35 ⇒ t ≈ 4 anos e 4 meses