Fundamentals Unit 2 Computer Systems HND in Computing

Fundamentals Unit 2 Computer Systems HND in Computing and Systems Development

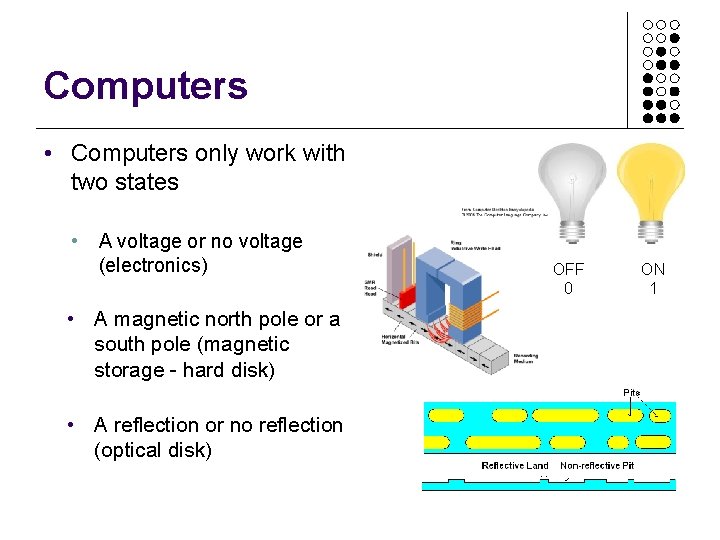
Computers • Computers only work with two states • A voltage or no voltage (electronics) • A magnetic north pole or a south pole (magnetic storage - hard disk) • A reflection or no reflection (optical disk) OFF 0 ON 1

Computers • So, everything we want a computer to do has to be represented by either a 0 or a 1 • • Numbers Colours Text Images Sound Video Instructions

Binary • Binary system has two values: 0 and 1 • When counting after a 1 we have to go the next place and start at 0 0001 0010 0011 0100 0101 0110 0111

Binary/decimal conversion • In this case we use powers of 2 (binary has 2 states) • • • In the first column from the right we multiply by 2 to power 0 = 1 In the second column we multiply by 2 to power 1 = 2 In the third column we multiply by 2 to power 2 = 4 and so on 264 232 216 28 24 22 21 20 128 64 32 16 8 4 2 1 We convert to decimal by adding the powers of 2 for each column where there is a 1 27 26 25 24 23 22 21 20 128 64 32 16 8 4 2 1 1 1 0 0 0 1 128+64+4+1 = 137

Binary/decimal conversion • Exercises 264 232 216 28 24 22 21 20 128 64 32 16 8 4 2 1 • • • 1111 = 0101 = 11110000 = • 1010 =

Computer arithmetic • The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple: 01101 + 10111 Rules of addition 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10

Bits and bytes • A 4 bit number has 16 combinations • An easier way to calculate is that there are 2 to the power 4 combinations 2 x 2 x 2 = 16 • A byte has 8 bits, so how many combination does that have?

Bytes • There are 256 combinations in a byte • Goes from 0000 to 1111 (0 to 255 in decimal) • It is tedious to write out bytes in binary

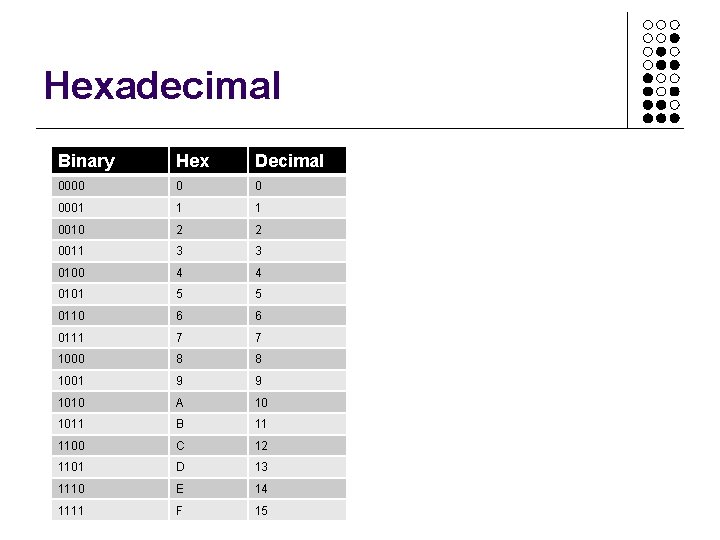
Hexadecimal • Hexadecimal is used to make it easier • We count up to 16 (remember 4 bits have 16 combinations) • 0 -9, then A, B, C, D, E, F

Hexadecimal Binary Hex Decimal 0000 0 0 0001 1 1 0010 2 2 0011 3 3 0100 4 4 0101 5 5 0110 6 6 0111 7 7 1000 8 8 1001 9 9 1010 A 10 1011 B 11 1100 C 12 1101 D 13 1110 E 14 1111 F 15

Hexadecimal notation • If we write 10 it may be binary, decimal or hex • Notations in use: • • 0 x 10 Unix based programming languages #101010 colour in HTML, CSS 10 h Intel assembler 10 h for text

Hexadecimal • We can split 8 bits into two 4 bit sections and convert to hex, so that a byte is represented by 2 hex digits • 36 d as a byte is 00100100 • Split this into to 4 bit sections 0010 0100 • Now convert each half to hex • 0010 = 2 and 0100 = 4 • So 36 d = 00100100 bin = 24 h

Hexadecimal • 16 bit examples 01011110101 = 0101 1110 = 5 E 10110011001 = = 1110011111001010 = = 1011 0101 B 5

Logic gates • Logic gates are the building blocks of the integrated circuits

Boolean logic Boolean algebra deals with the values 0 and 1 or the values false and true It is ideally suited for use in a computer Operations using just 0 and 1 can be easily replicated using simple electronic circuits

The simplest function - NOT The NOT gate takes an input and reverses it. If the input is 1, the output is 0 If the input is 0, the output is 1 INPUT OUTPUT Symbol A NOT A 0 1 1 0 Truth table

AND A 1 is required on both inputs to give a 1 at the output INPUT Symbol OUTPUT A B A AND B 0 0 1 1 1 Truth table

OR A 1 on either input gives a 1 at the output INPUT Symbol OUTPUT A B A OR B 0 0 1 1 1 0 1 1 Truth table

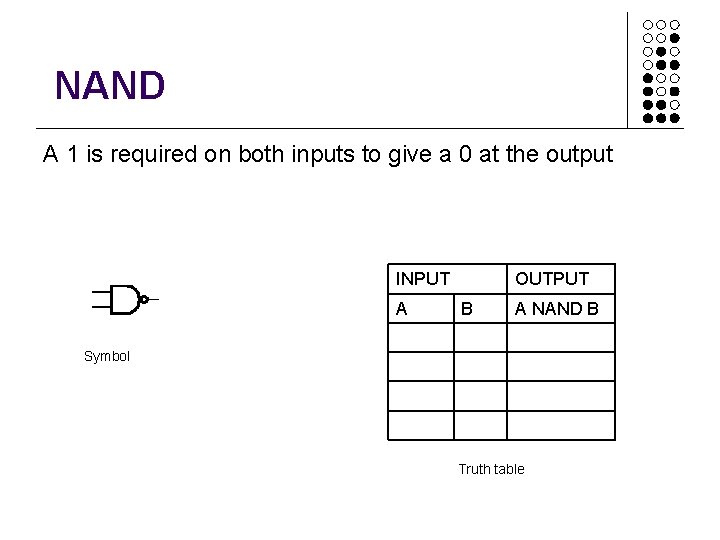
NAND A 1 is required on both inputs to give a 0 at the output INPUT A OUTPUT B A NAND B Symbol Truth table

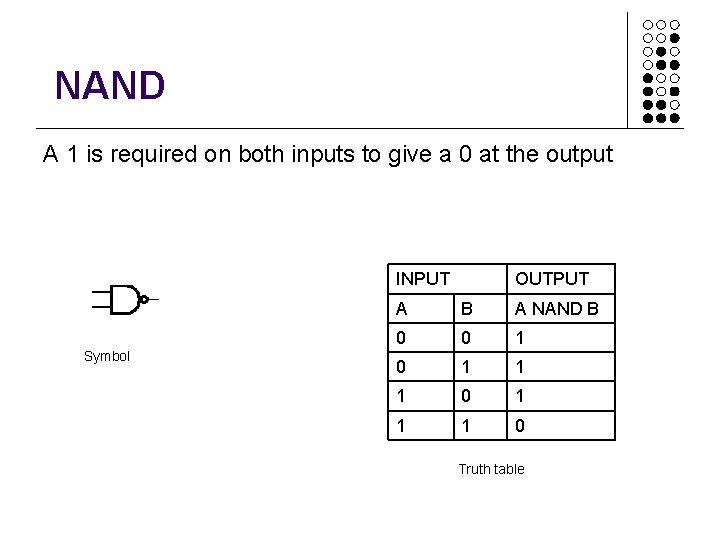
NAND A 1 is required on both inputs to give a 0 at the output INPUT Symbol OUTPUT A B A NAND B 0 0 1 1 1 0 Truth table

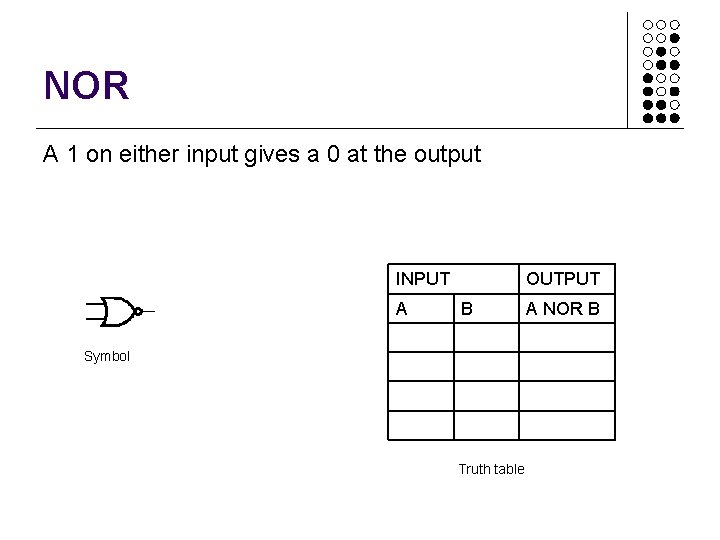
NOR A 1 on either input gives a 0 at the output INPUT A OUTPUT B Symbol Truth table A NOR B

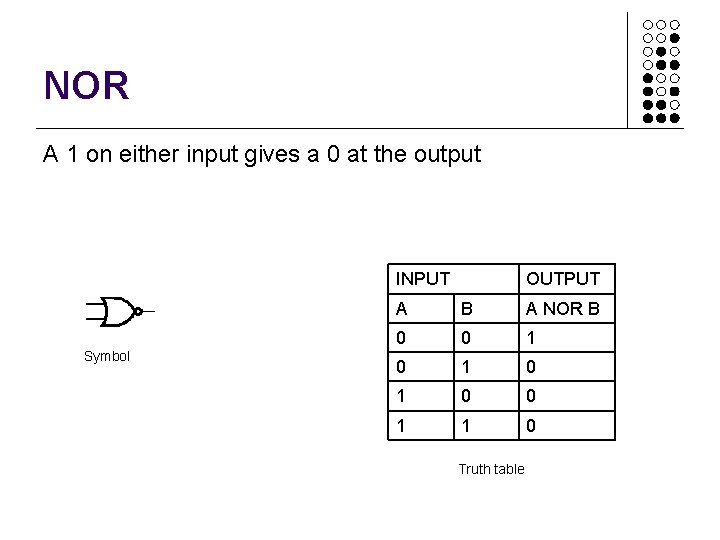
NOR A 1 on either input gives a 0 at the output INPUT Symbol OUTPUT A B A NOR B 0 0 1 0 1 0 0 1 1 0 Truth table

Exclusive OR You only get a 1 at the output when the two inputs are different INPUT Symbol OUTPUT A B A NOR B 0 0 1 1 1 0 Truth table

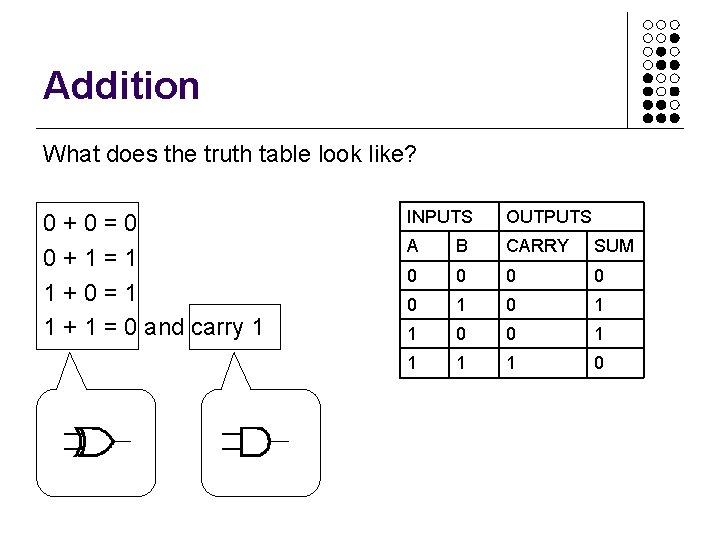
Addition So how can we use logic gates to add up? Remember the rules of binary arithmetic: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1

Addition Can we identify logic gates which do this? 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1

Addition An exclusive OR does the basic addition, with an AND for the carry 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1

Addition What does the truth table look like? 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1 INPUTS OUTPUTS A B CARRY SUM 0 0 0 1 1 0

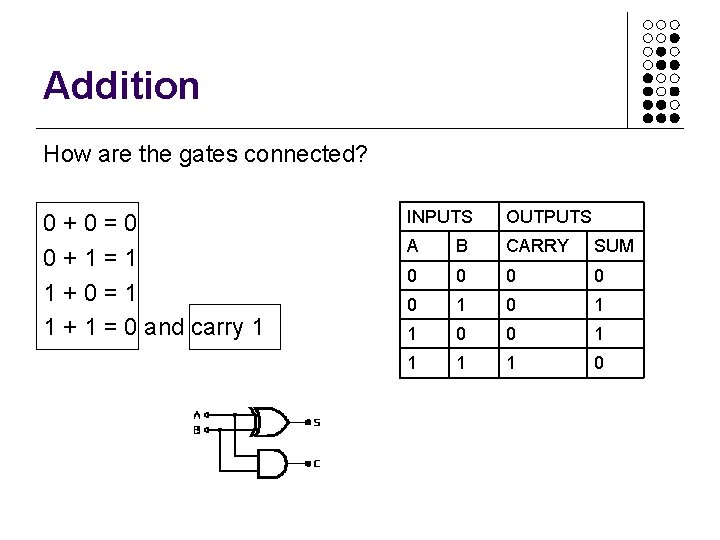
Addition How are the gates connected? 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1 INPUTS OUTPUTS A B CARRY SUM 0 0 0 1 1 0

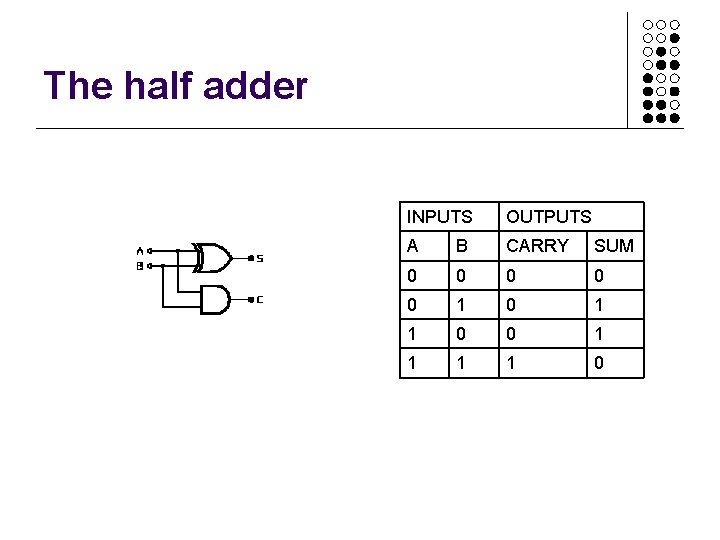
The half adder INPUTS OUTPUTS A B CARRY SUM 0 0 0 1 1 0

Why is it a half adder? • The half adder has two inputs • In order to make it useful it would have to have a third input – the carry in • Then it could do a full binary addition

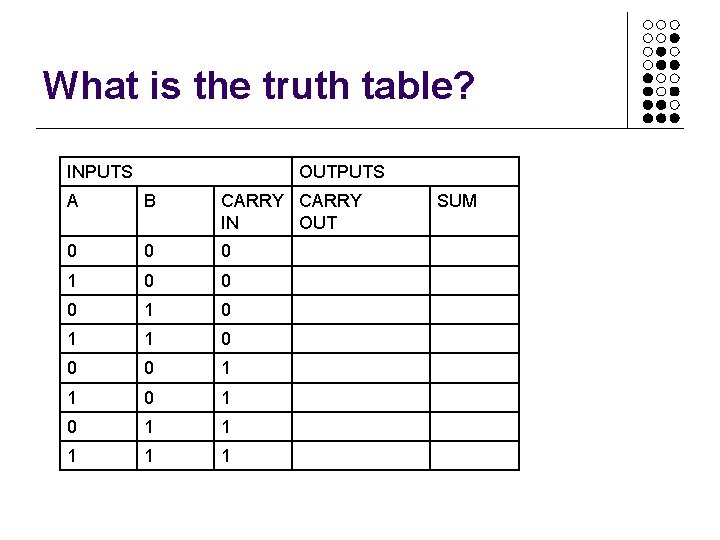
What is the truth table? INPUTS OUTPUTS A B CARRY IN OUT 0 0 0 1 0 1 1 0 0 0 1 1 1 SUM

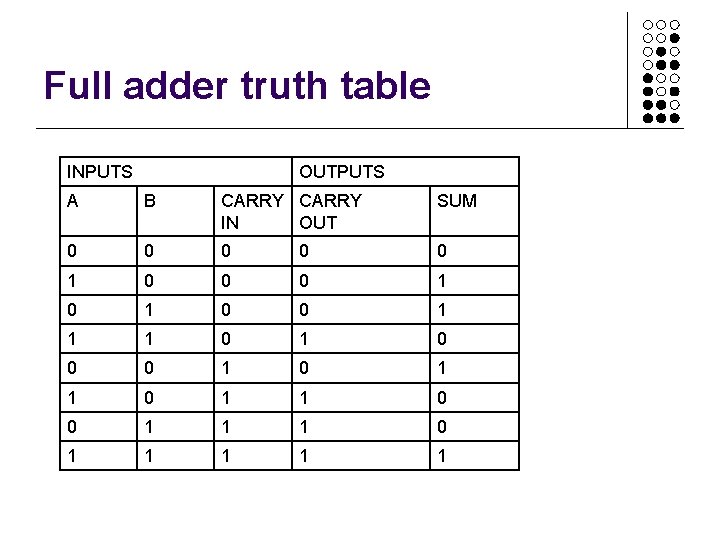
Full adder truth table INPUTS OUTPUTS A B CARRY IN OUT SUM 0 0 0 1 0 0 1 1 1 0 0 0 1 1 0 0 1 1 1 1 1

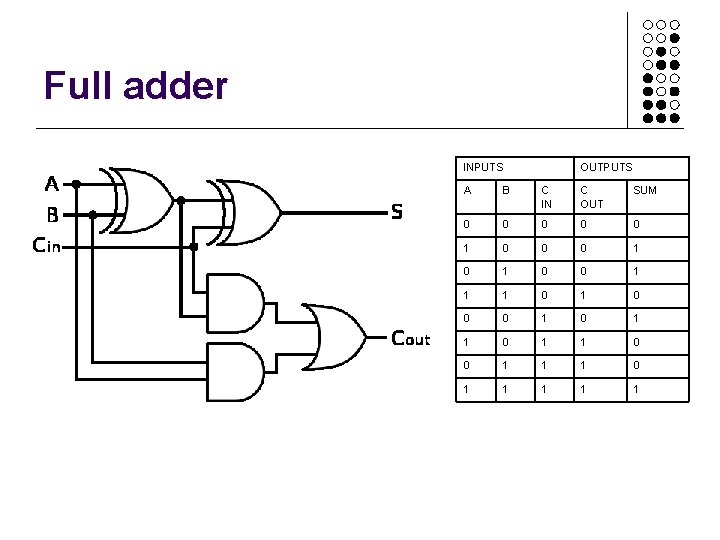
Full adder INPUTS OUTPUTS A B C IN C OUT SUM 0 0 0 1 0 0 1 1 1 0 0 0 1 1 0 0 1 1 1 1 1

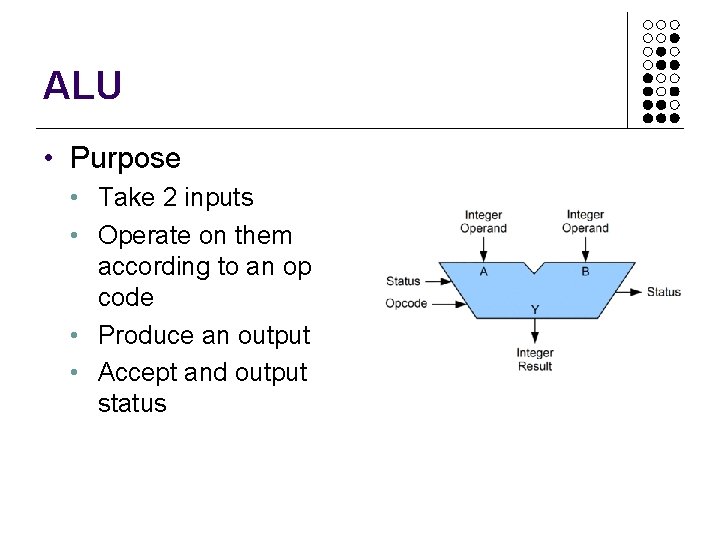
Arithmetic and logical unit (ALU) • A collection of logic gates • This is a 4 bit ALU

ALU • Purpose • Take 2 inputs • Operate on them according to an op code • Produce an output • Accept and output status

ALU operations • Arithmetic • • • Addition Subtraction Multiplication Division Can do far more than this depending on complexity • Logical • AND, OR, XOR etc

Registers • Where does the ALU get its inputs from and where does the output go? • Registers • Same size as CPU (16, 32, 64 bit) • Very fast • Connected to ALU by buses

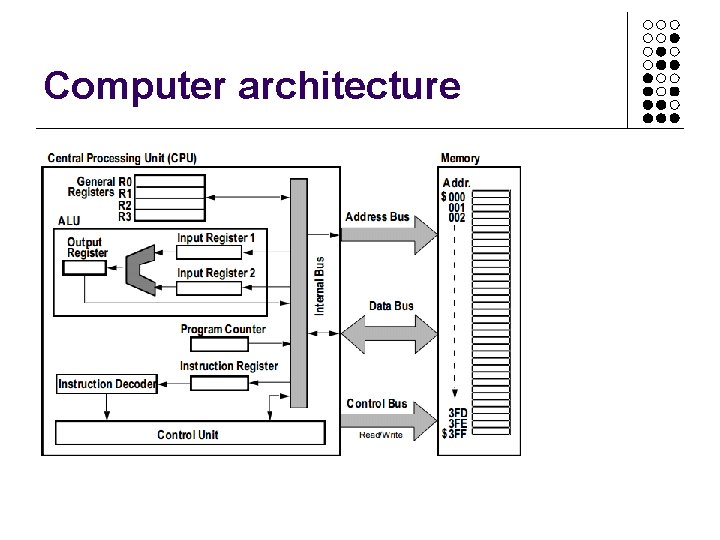
Architecture • We now know the hardware that does the work • But how does everything fit together? • Architecture defines that

Computer architecture

Let us look at TOM • Very simple simulator • • • 80 memory locations 16 instructions Keyboard input Printer output Can step through instructions Can show internal working