Fundamentals of Signals and Systems Signal a function



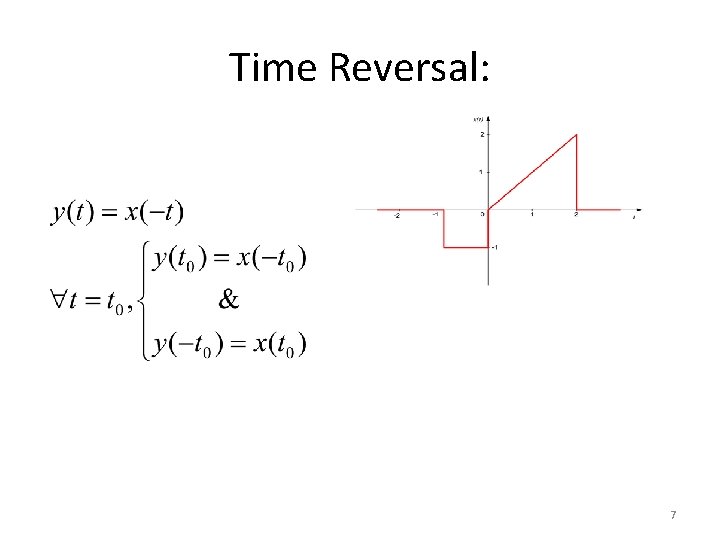








- Slides: 38

Fundamentals of Signals and Systems Ø Signal: a function of one or more variables that convey information on the nature of a physical phenomenon. Examples: v(t), i(t), x(t), heartbeat, blood pressure, temp. , vibration. • One-dimensional signals: function depends on a single variable, e. g. , speech signal • Multi-dimensional signals: function depends on two or more variables, e. g. , image

Ø System: an entity or operator that manipulates one or more signals to accomplish a function, thereby yielding new signals. Input signal Output signal System • Commonly encountered systems: communications systems Automatic speaker recognition system Aircraft landing system .

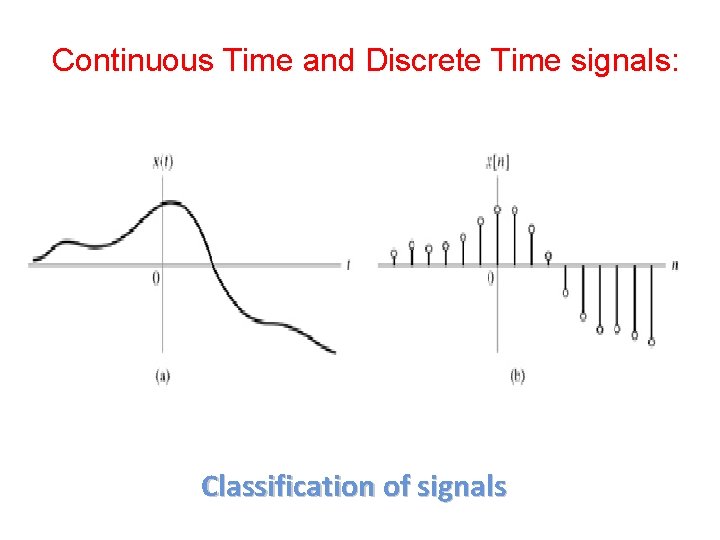
Continuous Time and Discrete Time signals: Classification of signals

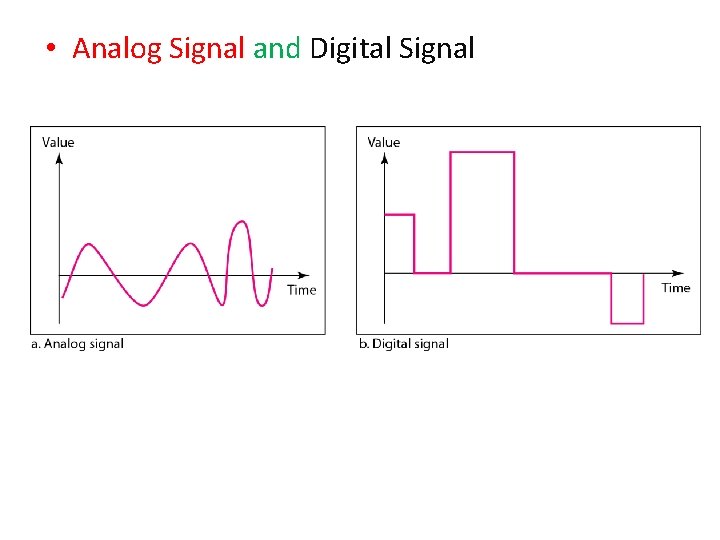
• Analog Signal and Digital Signal

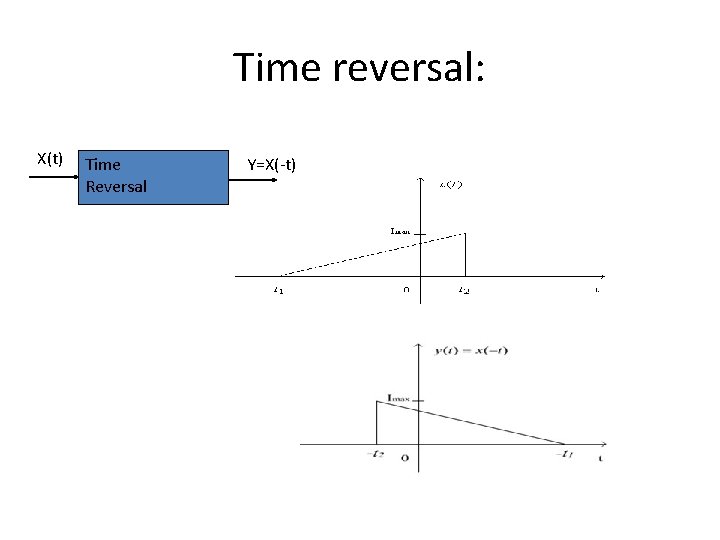
Time Reversal • Time reversal is also called time folding • In Time reversal signal is reversed with respect to time i. e. y(t) = x(-t) is obtained for the given function

Time reversal: X(t) Time Reversal Y=X(-t)
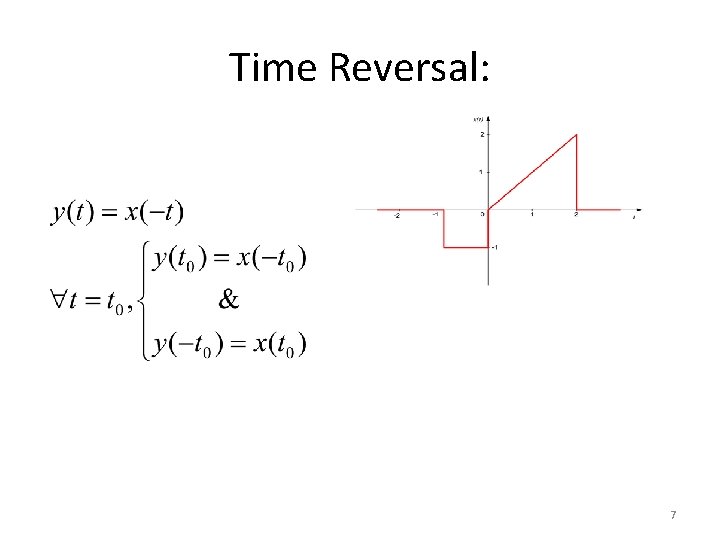
Time Reversal: 7

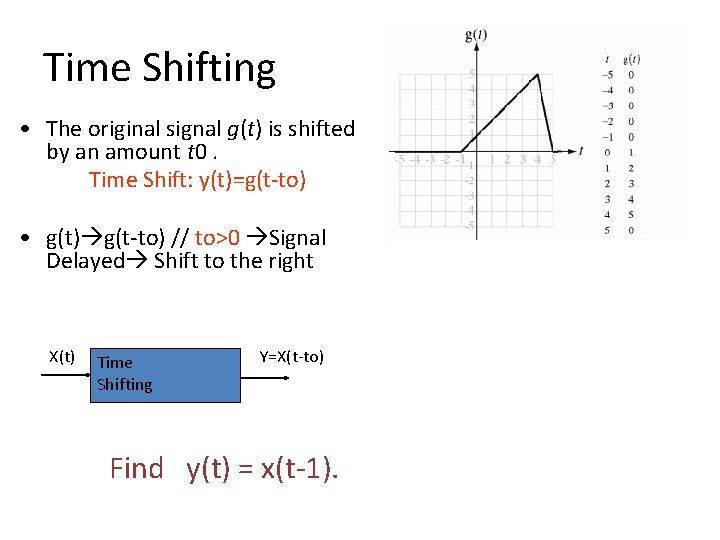
Time Shifting • The original signal x(t) is shifted by an amount t 0. Time Shift: y(t)=x(t-to) • X(t) X(t-to) // to>0 Signal Delayed Shift to the right • X(t) X(t+to) // to<0 Signal Advanced Shift to the left X(t) Time Shifting Y=X(t-to)

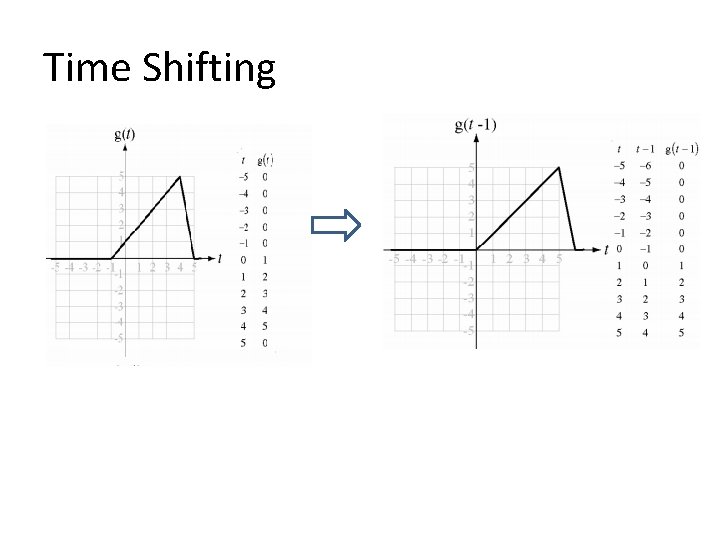
Time Shifting • The original signal g(t) is shifted by an amount t 0. Time Shift: y(t)=g(t-to) • g(t) g(t-to) // to>0 Signal Delayed Shift to the right X(t) Time Shifting Y=X(t-to) Find y(t) = x(t-1). Delay

Time Shifting

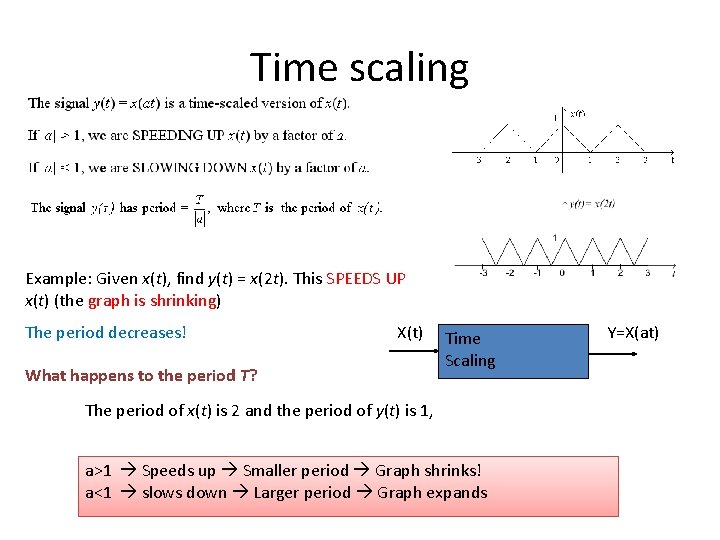
Time scaling Example: Given x(t), find y(t) = x(2 t). This SPEEDS UP x(t) (the graph is shrinking) The period decreases! X(t) What happens to the period T? Time Scaling The period of x(t) is 2 and the period of y(t) is 1, a>1 Speeds up Smaller period Graph shrinks! a<1 slows down Larger period Graph expands Y=X(at)

Time Scaling |a| > 1 – Speed Up |a| < 1 – Slow Down 05 June 2021 12

Time scaling • Given y(t), – find w(t) = y(3 t) – v(t) = y(t/3).

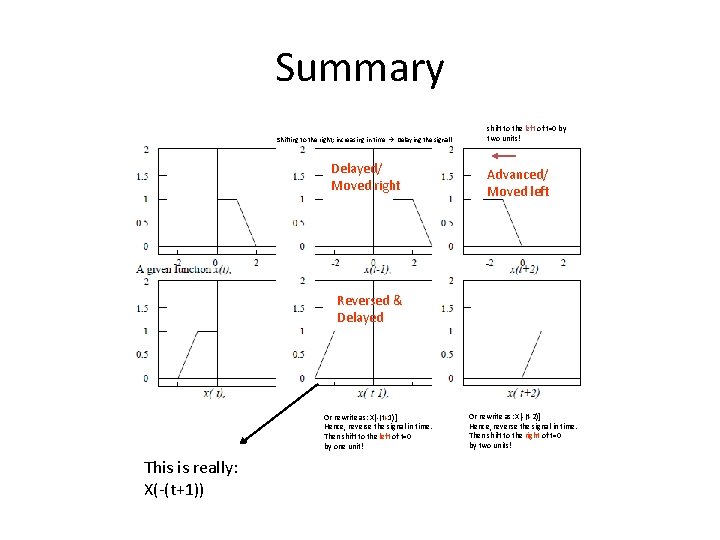
Summary Shifting to the right; increasing in time Delaying the signal! Delayed/ Moved right shift to the left of t=0 by two units! Advanced/ Moved left Reversed & Delayed Or rewrite as: X[-(t+1)] Hence, reverse the signal in time. Then shift to the left of t=0 by one unit! This is really: X(-(t+1)) Or rewrite as: X[-(t-2)] Hence, reverse the signal in time. Then shift to the right of t=0 by two units!

Symmetric about the y axis FUNCTIONS Symmetric about the origin

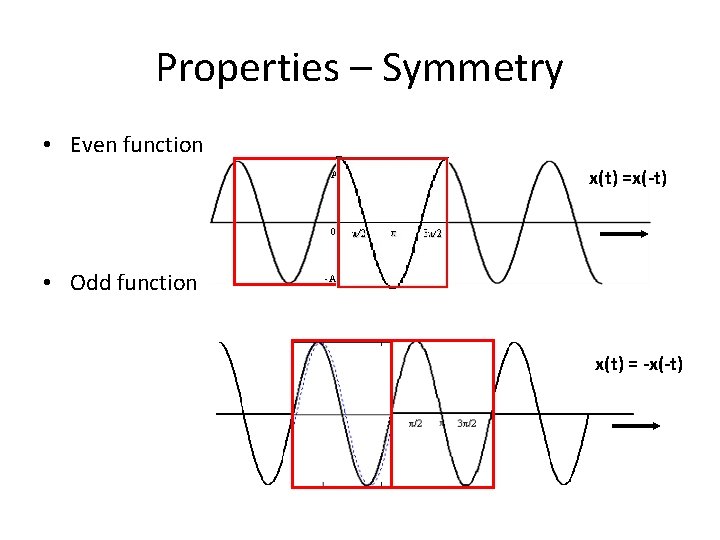
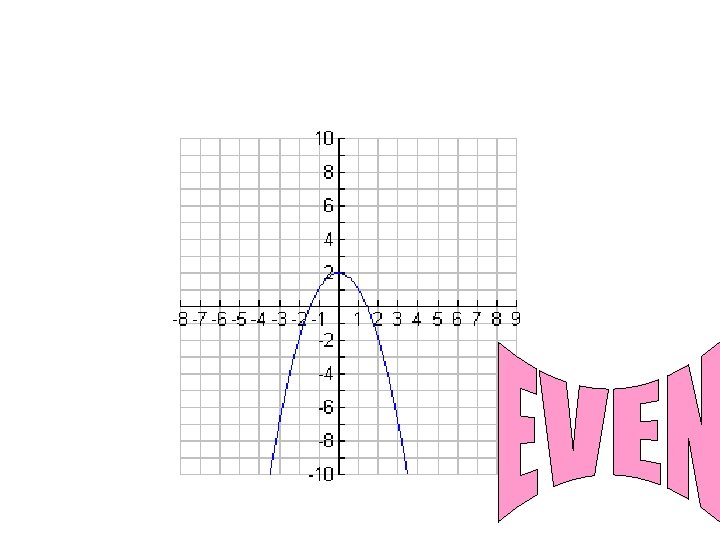
Properties – Symmetry • Even function x(t) =x(-t) A 0 • Odd function π π/2 3π/2 -A f(-t) = -f(t) A 0 A x(t) = -x(-t) π/2 π 3π/2

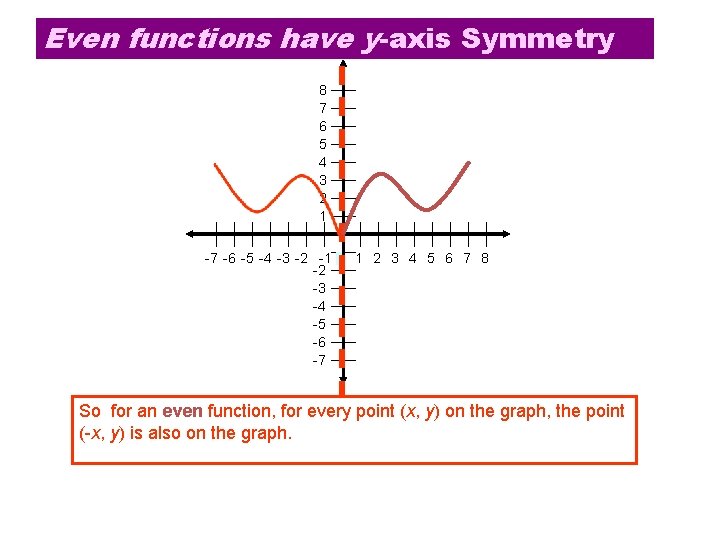
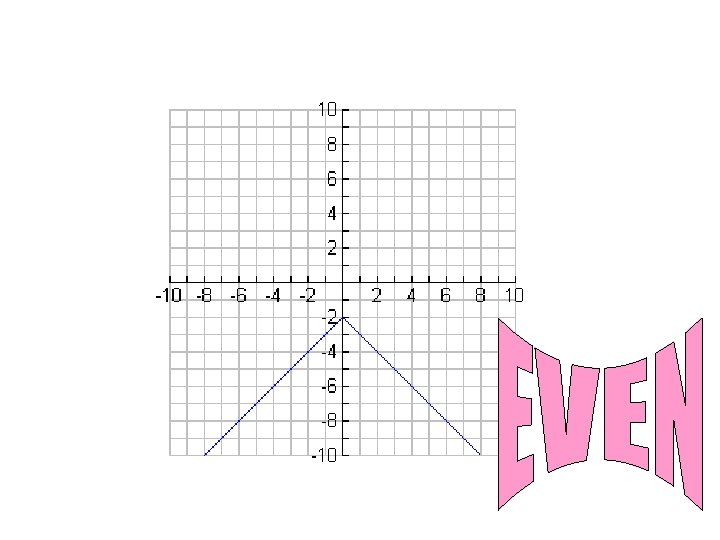
Even functions have y-axis Symmetry 8 7 6 5 4 3 2 1 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 So for an even function, for every point (x, y) on the graph, the point (-x, y) is also on the graph.

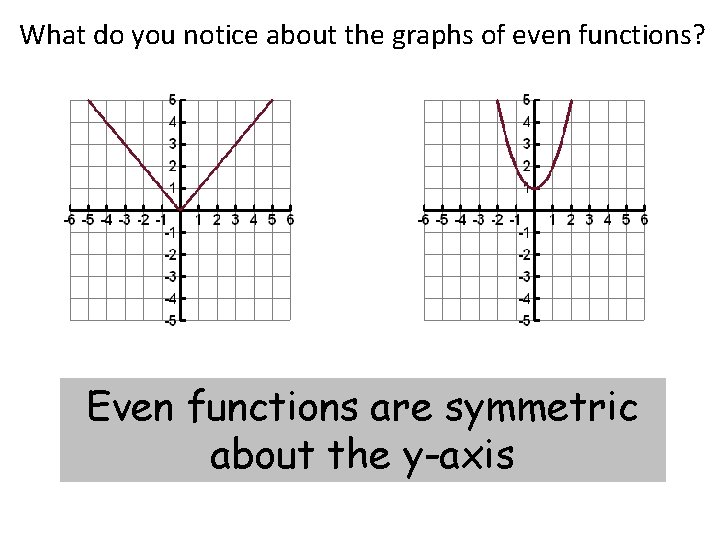
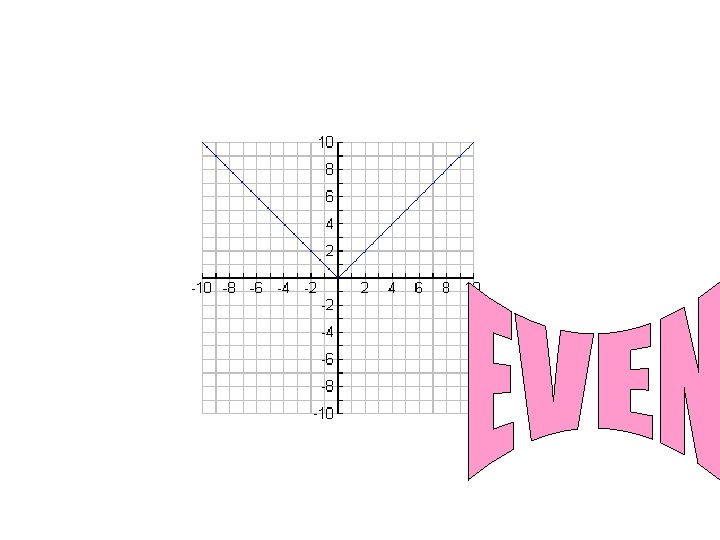
What do you notice about the graphs of even functions? Even functions are symmetric about the y-axis

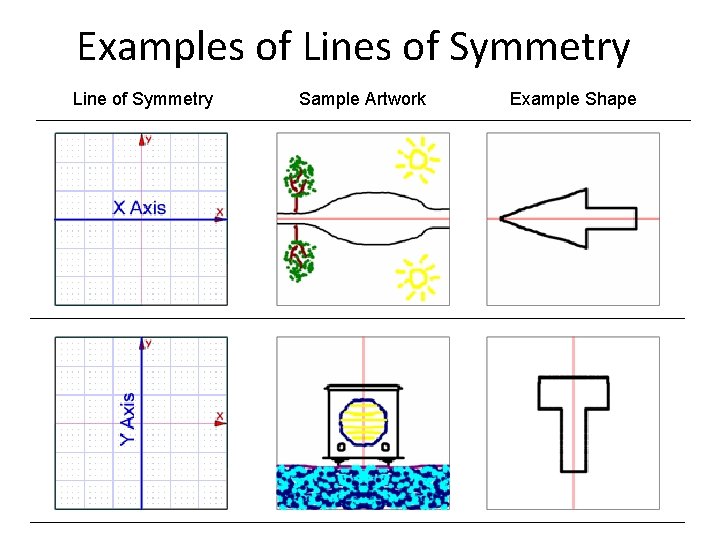
Examples of Lines of Symmetry Line of Symmetry Sample Artwork Example Shape

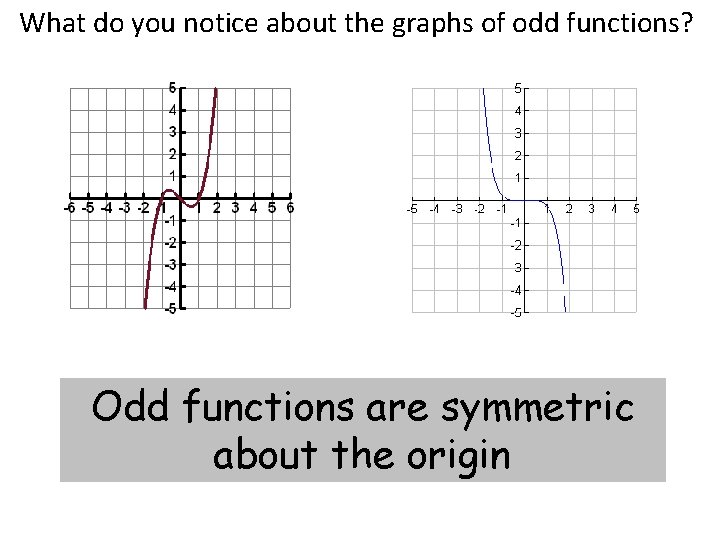
What do you notice about the graphs of odd functions? Odd functions are symmetric about the origin

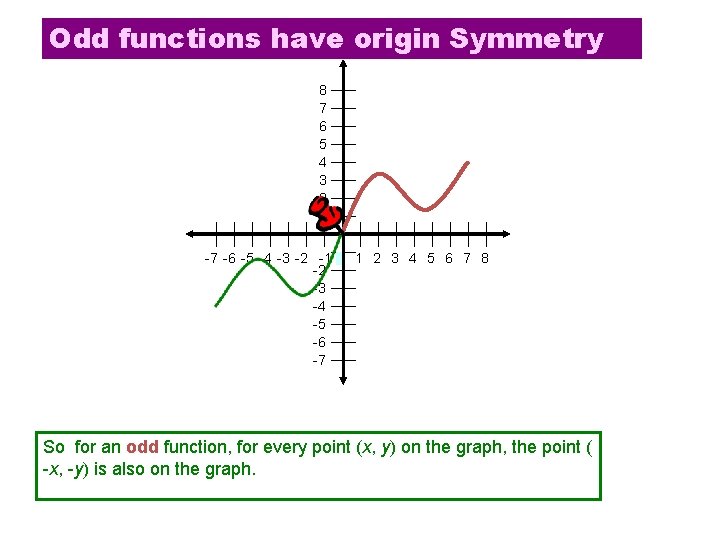
Odd functions have origin Symmetry 8 7 6 5 4 3 2 1 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 -2 -3 -4 -5 -6 -7 So for an odd function, for every point (x, y) on the graph, the point ( -x, -y) is also on the graph.

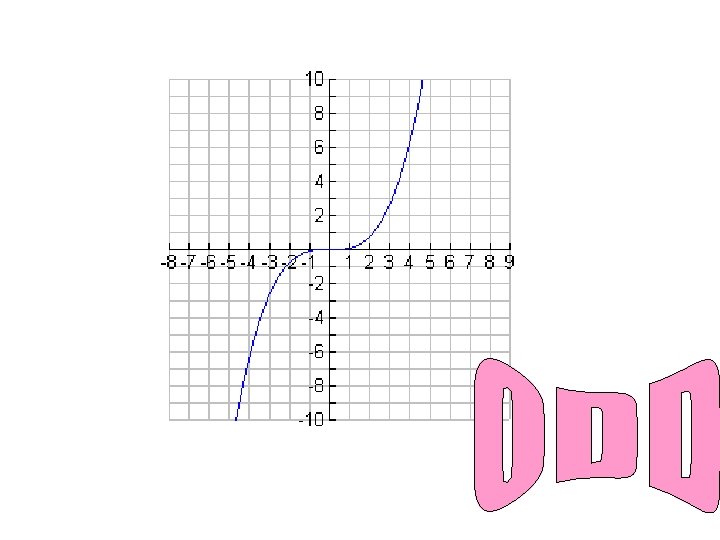
A function is even if f (x) = f (-x) for every number x in the domain. So if you plug a –x into the function and you get the original function back again it is even. Is this function even? YES Is this function even? NO

A function is odd if f (x) = - f (-x) for every number x in the domain. So if you plug a –x into the function and you get the negative of the function back again (all terms change signs) it is odd. Is this function odd? NO Is this function odd? YES

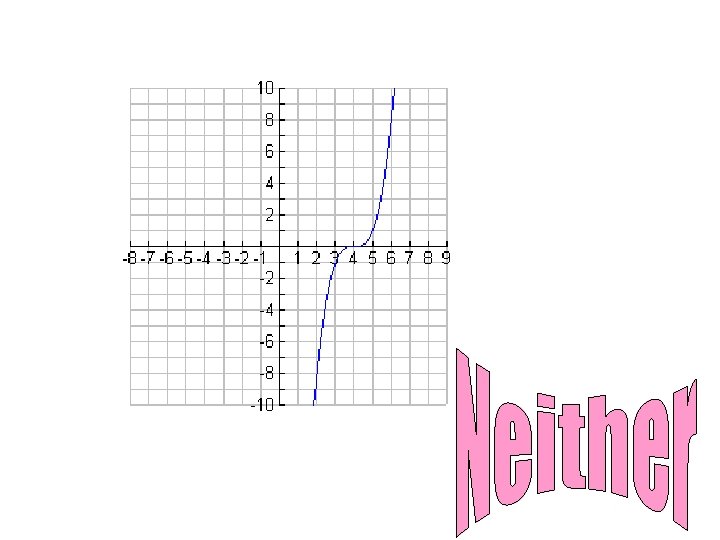
If a function is not even or odd we just say neither (meaning neither even nor odd) Determine if the following functions are even, odd or neither. Not the original and all terms didn’t change signs, so NEITHER. Got f(x) back so EVEN.









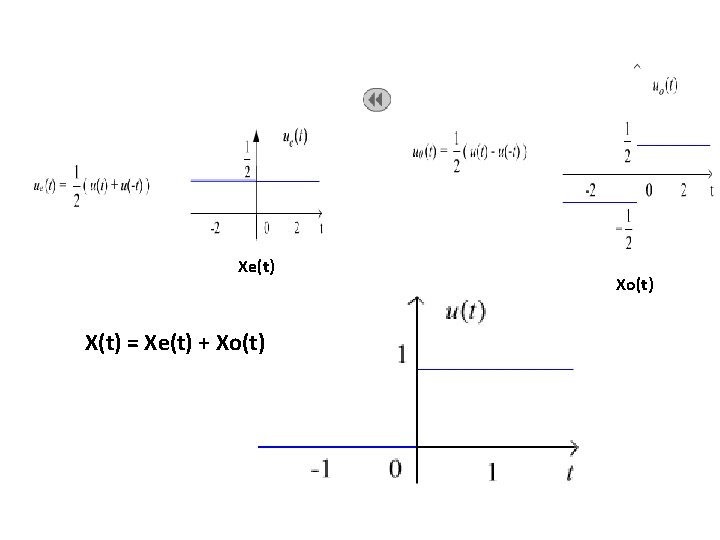
Signal Characteristics • Even and odd signals 1. X(t) = Xe(t) + Xo(t) • Properties Xe + Ye = Ze Xo + Yo = Zo Xe + Yo = Ze + Zo Know These! Xe * Ye = Ze Xo * Yo = Ze Xe * Yo = Zo

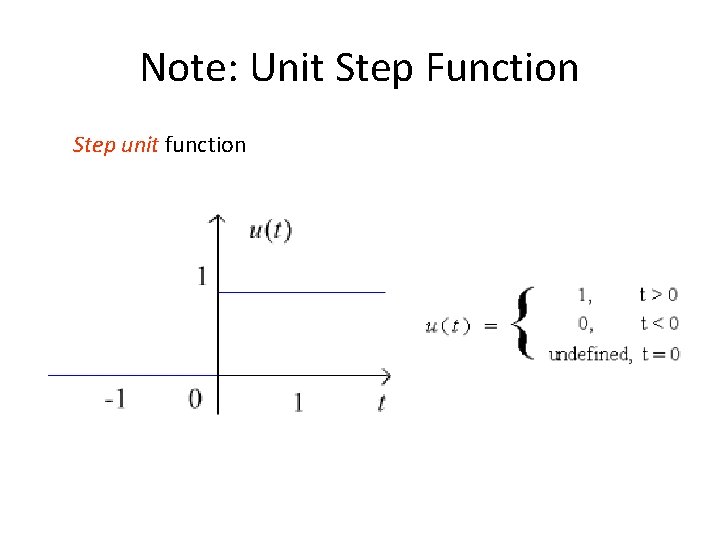
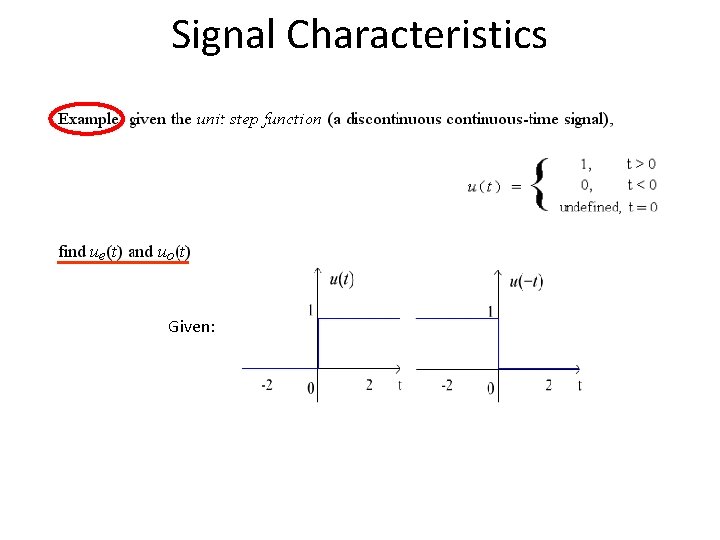
Note: Unit Step Function Step unit function

Signal Characteristics Given:

Signal Characteristics Symmetric across the vertical axis Anti-symmetric across the vertical axis

Xe(t) X(t) = Xe(t) + Xo(t)

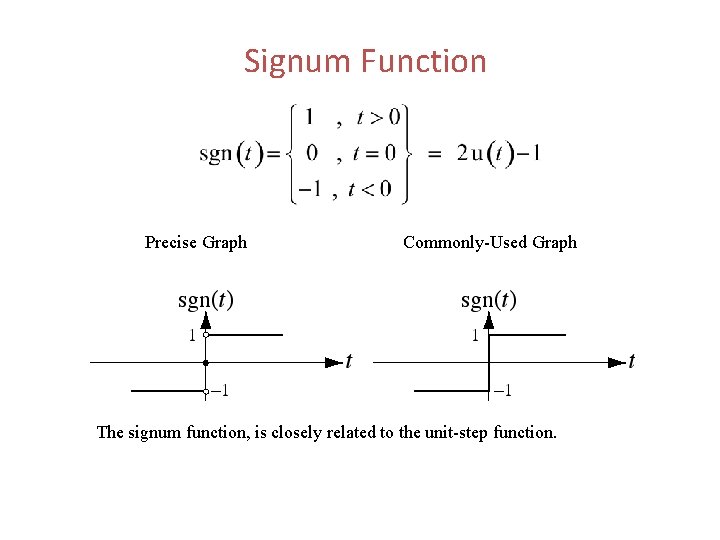
Signum Function Precise Graph Commonly-Used Graph The signum function, is closely related to the unit-step function.