Fundamentals of Semiconductor Devices Anderson and Anderson Mc














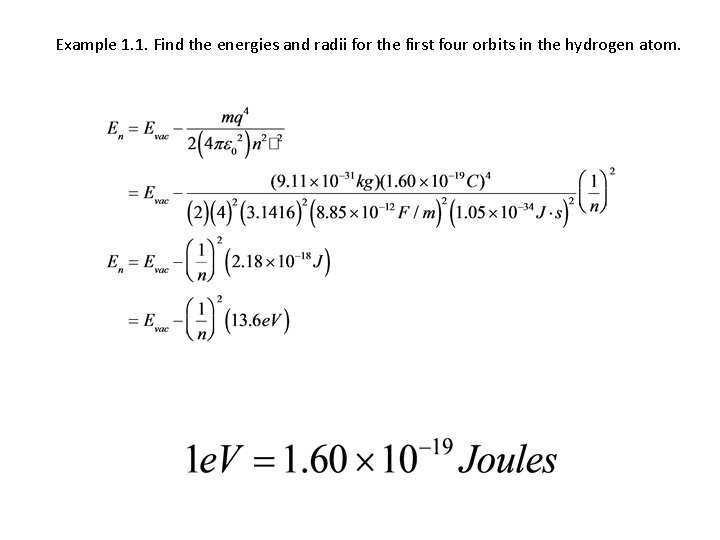
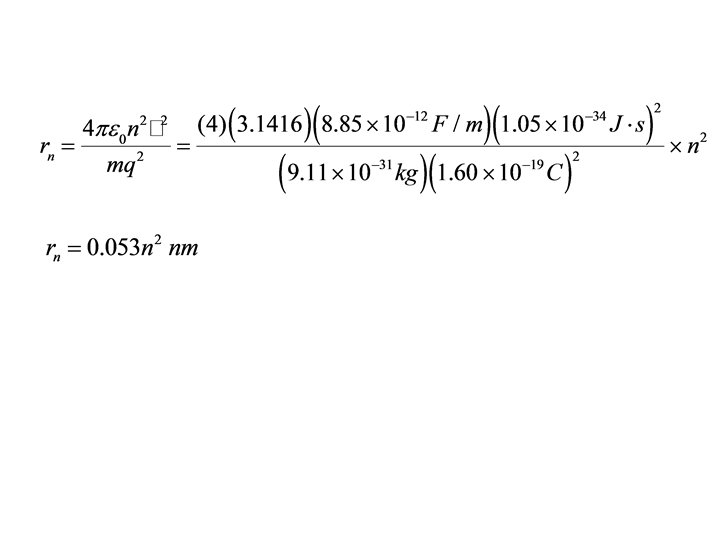




















































































- Slides: 150

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Introduction and Preview Chapter 1 Section 1 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Overview • • • Part 1: Materials Part 2: Diodes Part 3: Field-effect Transistors Part 4: Bipolar Junction Transistors Part 5: Optoelectronic Devices • Each Part has one or more Supplements

Part 1 Materials • Chapter 1: Electron Energy and States in Semiconductors • Chapter 2: Homogeneous Semiconductors • Chapter 3: Current Flow in Homogeneous Semiconductors • Chapter 4: Nonhomogeneous Semiconductors • Supplement 1 A: Intro to Quantum Mechanics • Supplement 1 B: Additional Topics on Materials

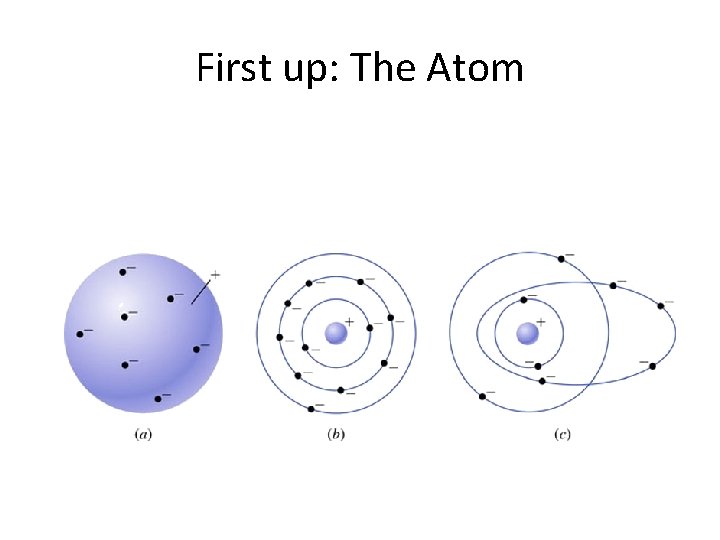
Chapter 1: Electron Energy and States in Semiconductors • Will learn fundamental physics of how electrons behave in matter – Need this to understand how to control them to create useful electronic devices – Take into account temperature, impurities, applied voltages, device structures, optical radiation • Matter created of atoms, so start with the atom

Will need quantum mechanics • Because of small scale, we’ll need to use quantum mechanics – Will present some results in Chapter 1 – Much more detail in Supplement A to Part 1 • We will apply “pseudo-classical” mechanics – Way to apply familiar classical mechanical laws – Helps us use our intuition – Have to create “effective” quantities such as “effective mass” that replace real mass in classical equations

First up: The Atom

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill A Brief History (of atomic models) Chapter 1 Section 2 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

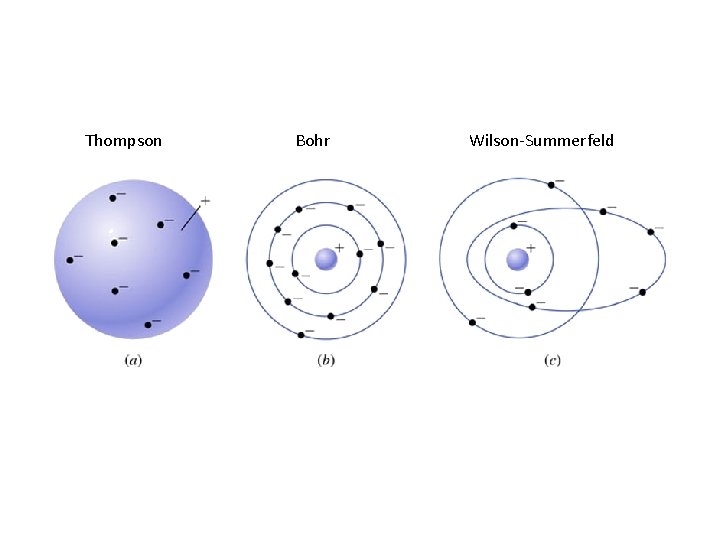
Thompson Bohr Wilson-Summerfeld

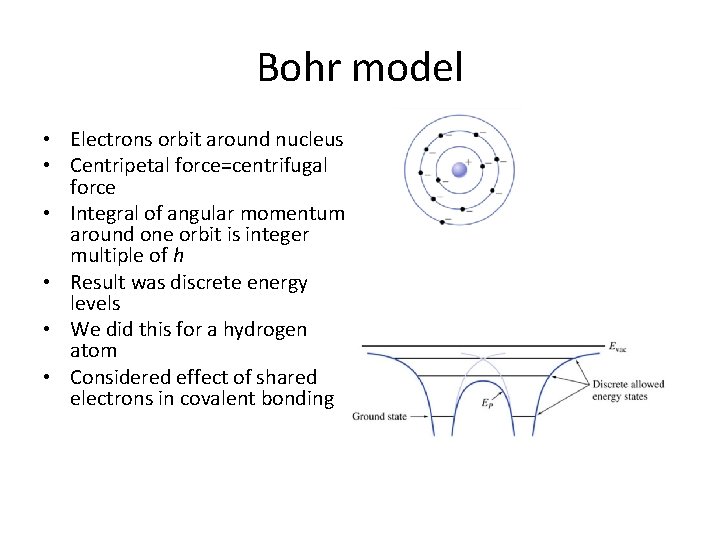
Key points • Bohr model assumes electron orbits are circular • For orbits to be stable, energies have to be quantized – Stable means centrifugal force equal to centripetal force – Quantized means integral of angular momentum around one orbit is integer multiple of Plancks’ constant • Planck’s constant is • Wilson-Sommerfeld model allows orbits to be elliptical • Next up: Bohr model for the hydrogen atom

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Bohr Model for the Hydrogen Atom Chapter 1 Section 3. 1 Part A: The derivation Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Roadmap • Orbits are circular • Centrifugal force must equal centripetal force for orbit to be stable • Integral of angular momentum around one orbit is quantized • Result – Quantized radii – Quantized velocities – Quantized energies • We’ll apply to hydrogen atom

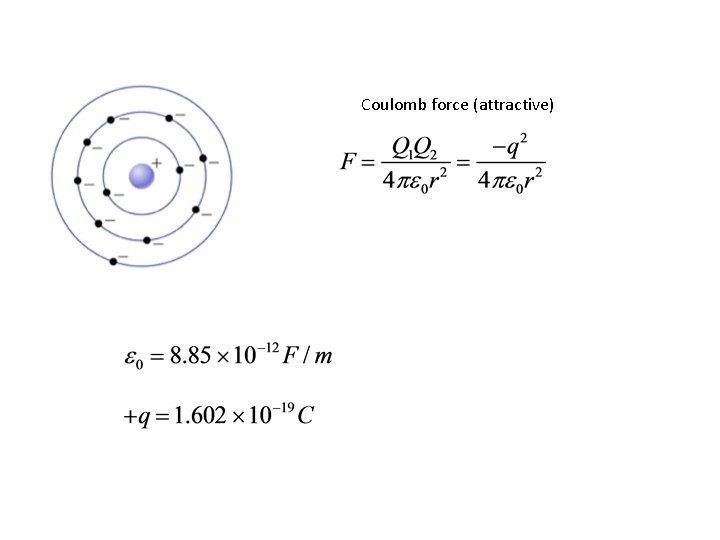
Coulomb force (attractive)

Repeat after me: The force is minus the gradient of the potential energy We had:

• • • Integrate both sides There will be a constant of integration Choose a reference for the potential energy Coulomb force at r=∞ is zero Choose r=∞ as reference point


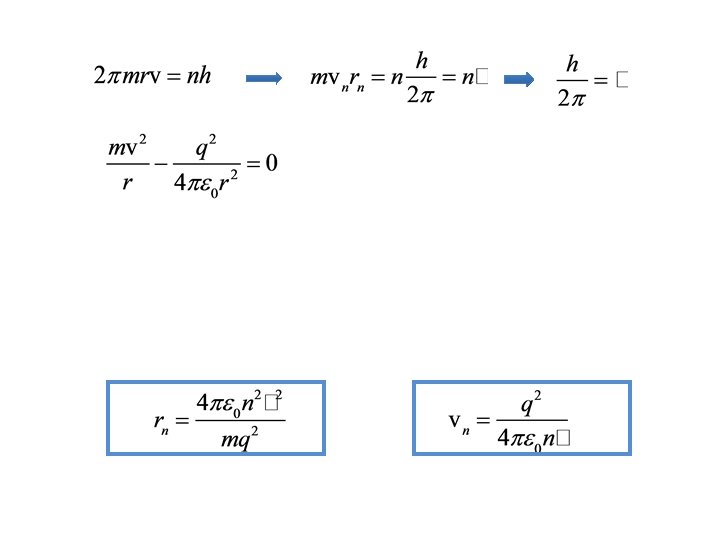
For atom to be stable, centrifugal force must equal attractive (Coulomb) force Centrifugal force Coulomb force Bohr also postulated that the integral of the angular momentum around one complete orbit is an integer multiple of Planck's constant h:


We want the energies

Key points so far • Bohr assumed orbits were circular • Integral of angular momentum around one orbit is an integer multiple of h • The force is minus the gradient of the potential energy • The reference for potential energy is arbitrary • To be stable, centrifugal force must equal centripetal force (Coulomb force) • Results in quantized radii, velocities, and energies • Next up: some examples

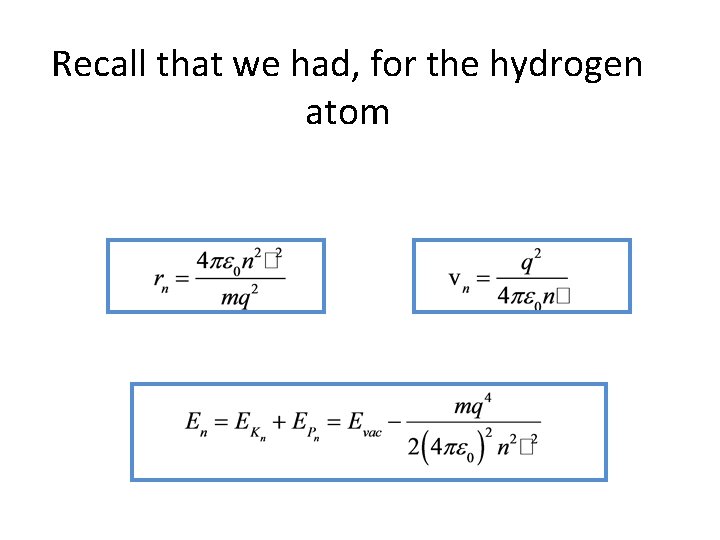
Recall that we had, for the hydrogen atom
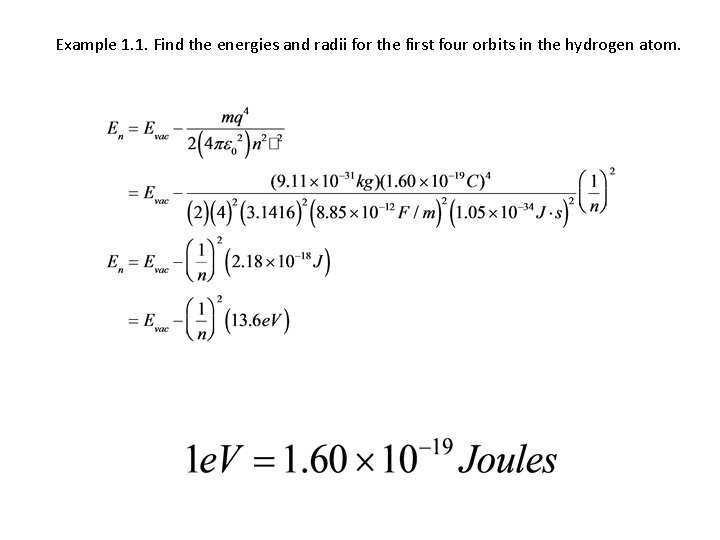
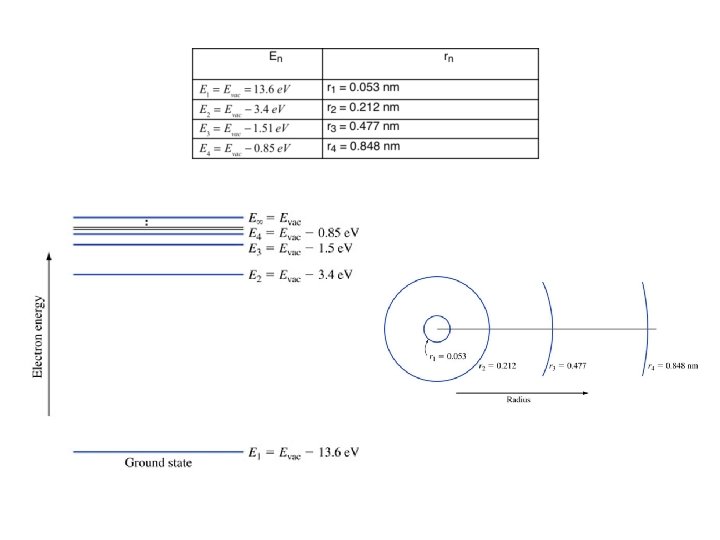
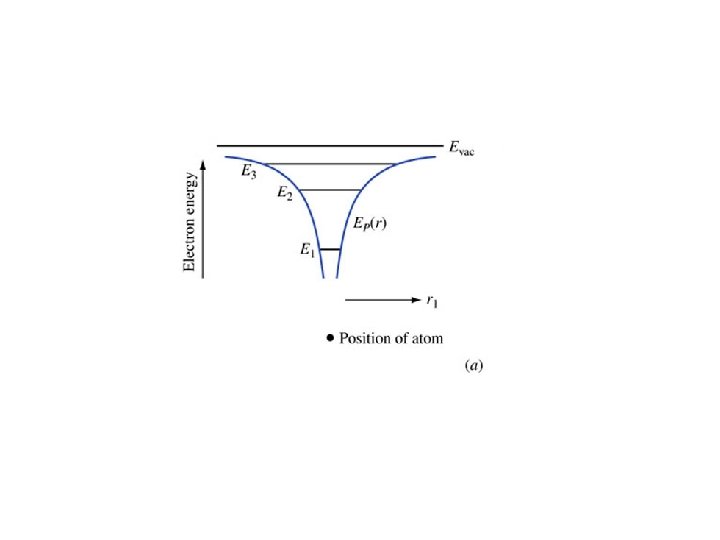
Example 1. 1. Find the energies and radii for the first four orbits in the hydrogen atom.
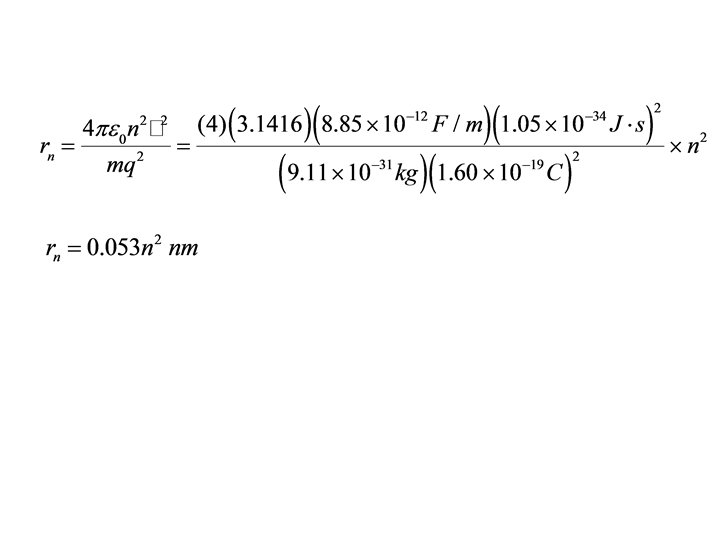


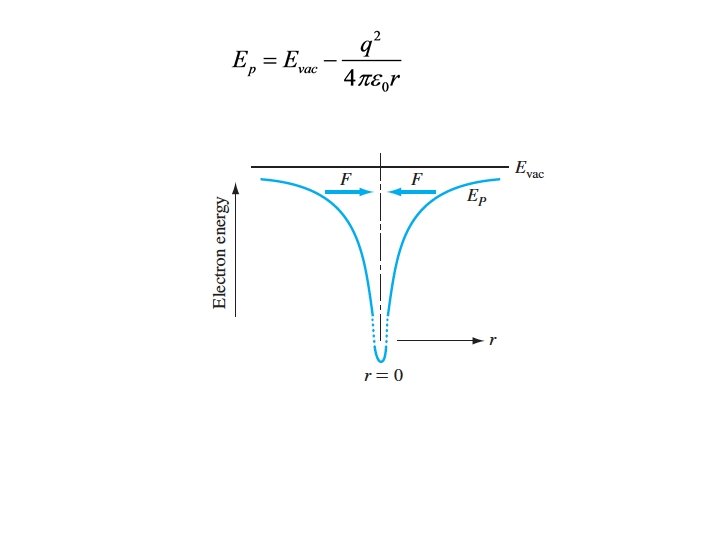
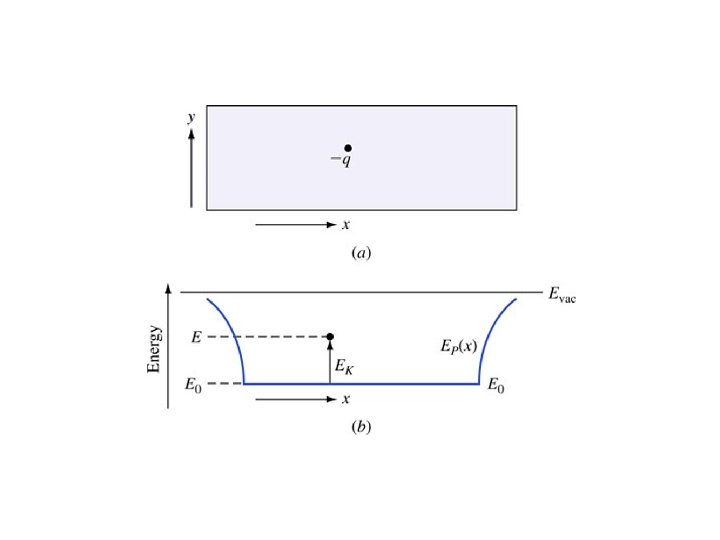
The energy of a state must always be expressed as an energy difference– the difference between the energy of the state and some known reference. e. g. , Evac-E.

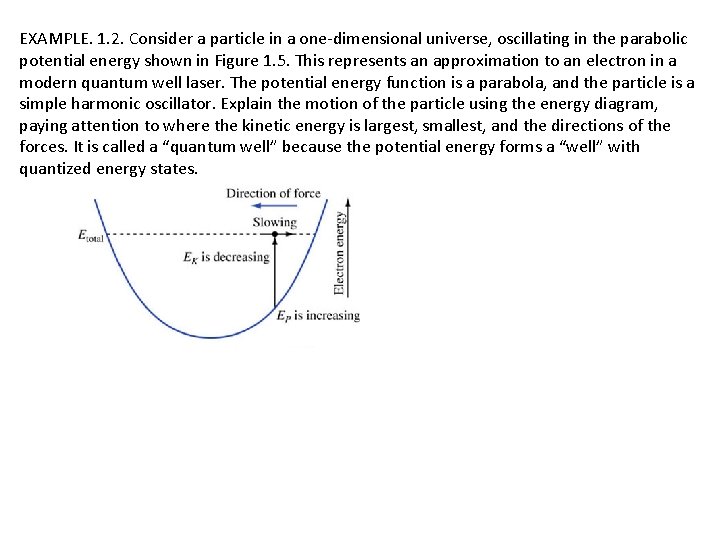
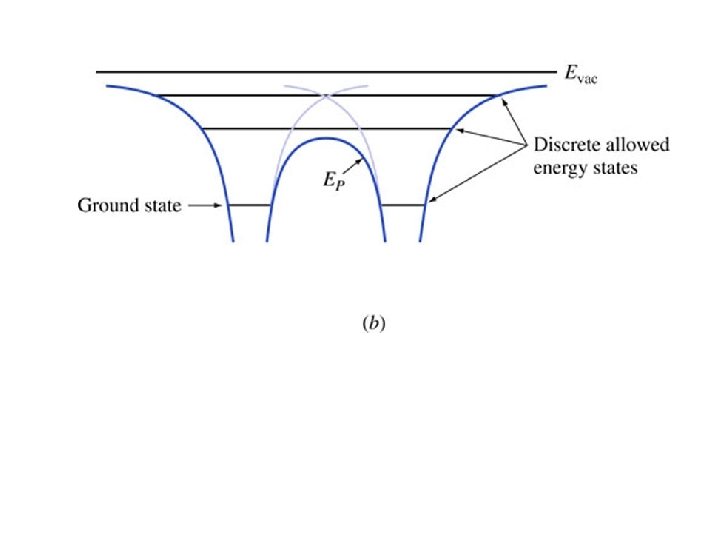
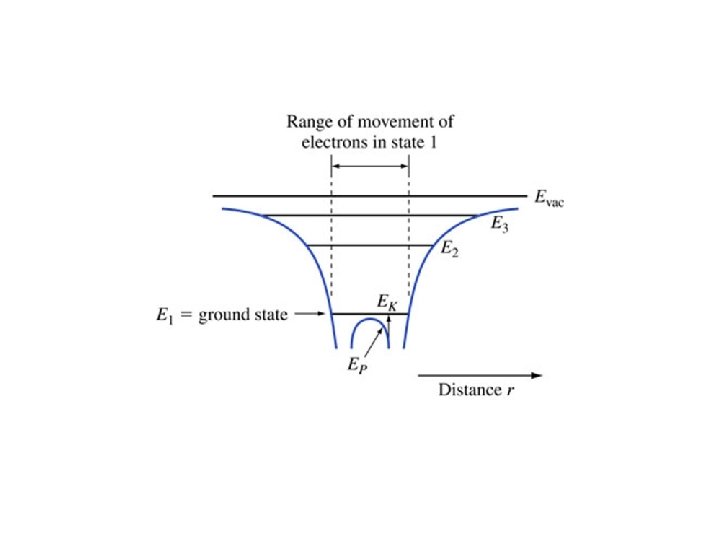
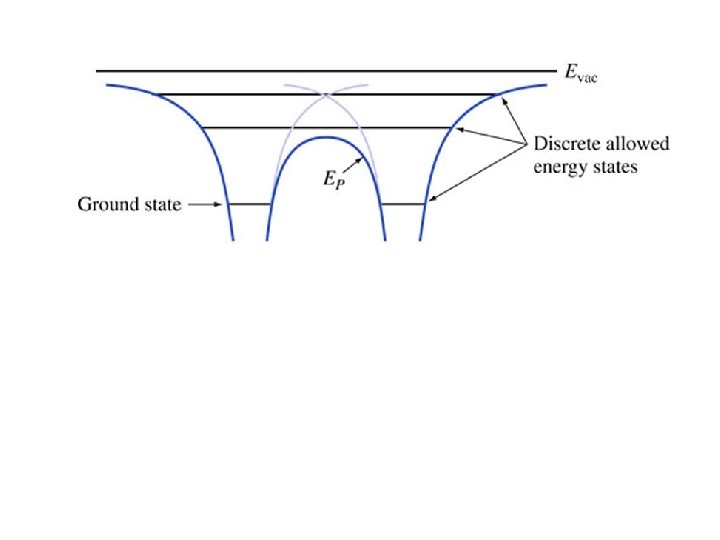
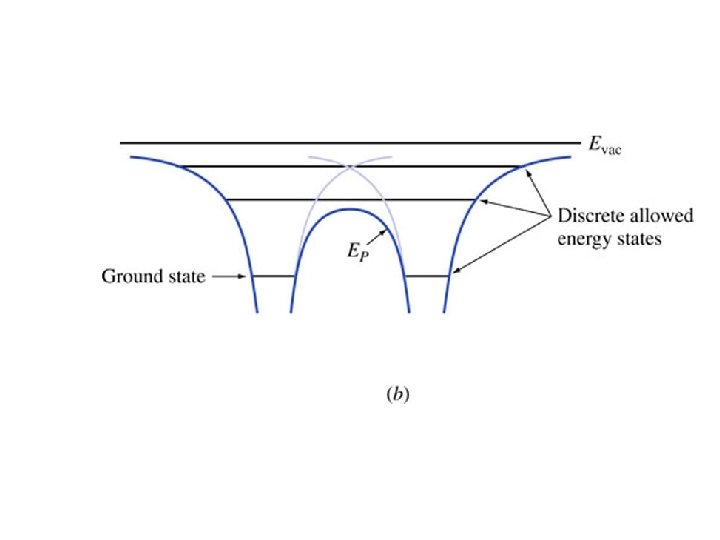
EXAMPLE. 1. 2. Consider a particle in a one-dimensional universe, oscillating in the parabolic potential energy shown in Figure 1. 5. This represents an approximation to an electron in a modern quantum well laser. The potential energy function is a parabola, and the particle is a simple harmonic oscillator. Explain the motion of the particle using the energy diagram, paying attention to where the kinetic energy is largest, smallest, and the directions of the forces. It is called a “quantum well” because the potential energy forms a “well” with quantized energy states.

Key points • Radii gets increasing large with increasing n • Energies increase with n – They get closer together approaching Evac • Electrons travel at constant energy (conservation of energy) • The force is minus the gradient of the potential energy • Coming up: applying all this to molecules and later to crystals (such as silicon)

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Application to Molecules: Covalent Bonding Chapter 1 Section 3. 2 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

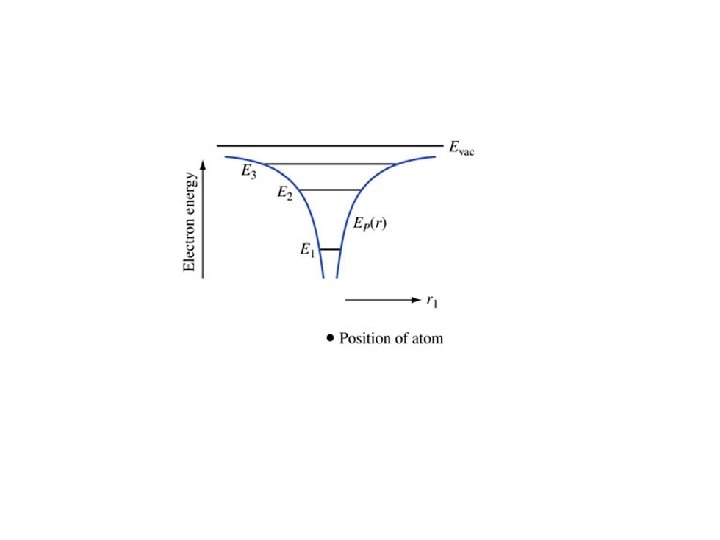
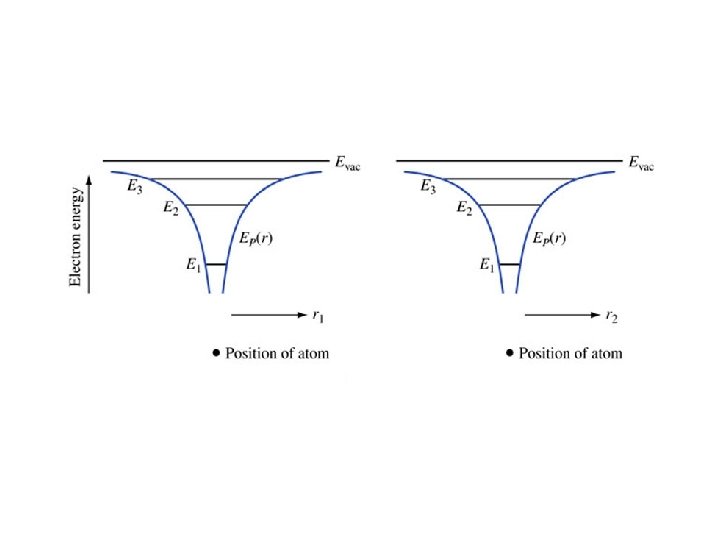
Bohr model • Assumed positive charges in the center of the atom • Assumed electron orbits are circular • Took integral of angular momentum around one orbit to be quantized • Result was discrete energy states • We derived it for a single hydrogen atom






Key points • When two atoms get close enough together, their potential energies sum • The molecule may have some bound states • States shared between the atoms help keep the molecule together • There is some stable distance

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Quantum Numbers and the Pauli Exclusion Principle Chapter 1 Section 3. 3 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display


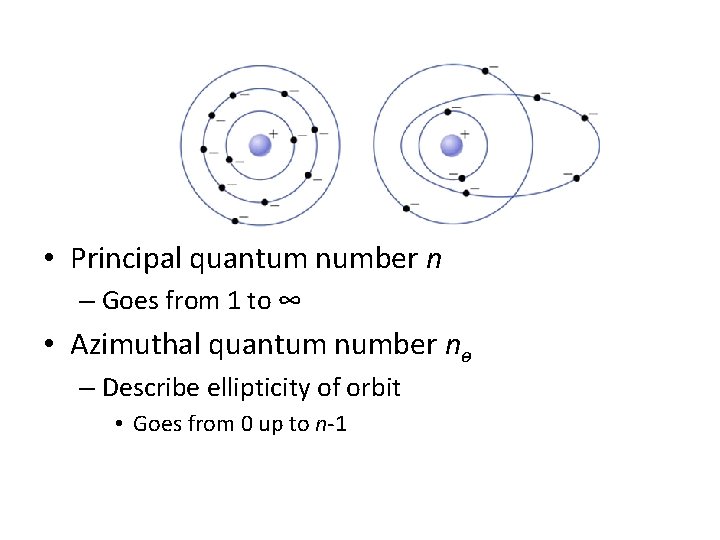
• Principal quantum number n – Goes from 1 to ∞ • Azimuthal quantum number nɵ – Describe ellipticity of orbit • Goes from 0 up to n-1

Additional quantum numbers • Tilt of orbit m – Can go from -nɵ up to nɵ • Spin s – Can be +1/2 or -1/2 • The exact combination of quantum numbers of a state determine the energy – Except spin, which has no effect

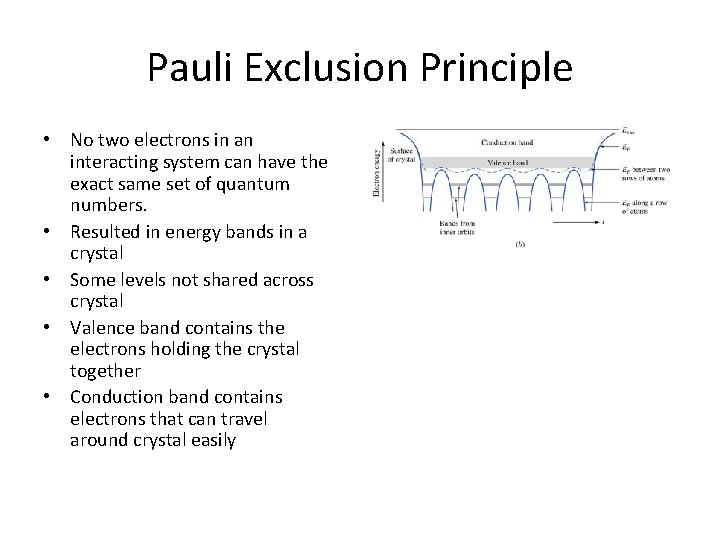
Pauli Exclusion Principle No two electrons in an interacting system can have the exact same set of quantum numbers.

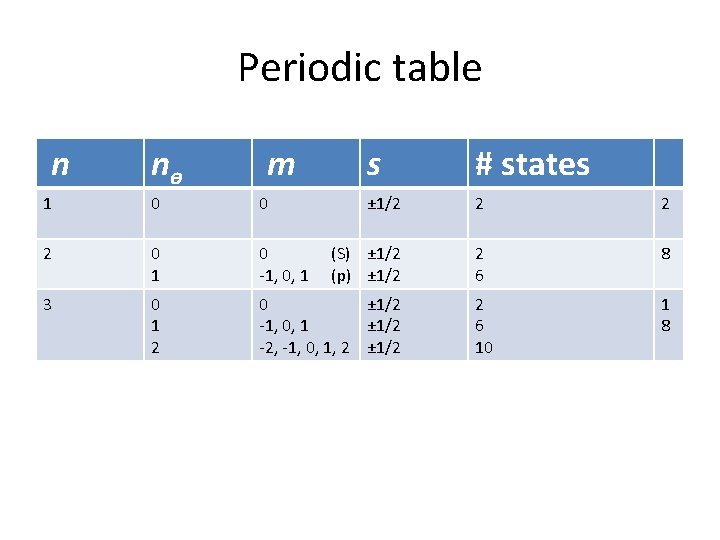
Periodic table n nɵ m s # states ± 1/2 2 2 (S) ± 1/2 (p) ± 1/2 2 6 8 2 6 10 1 8 1 0 0 2 0 1 0 -1, 0, 1 3 0 1 2 0 ± 1/2 -1, 0, 1 ± 1/2 -2, -1, 0, 1, 2 ± 1/2

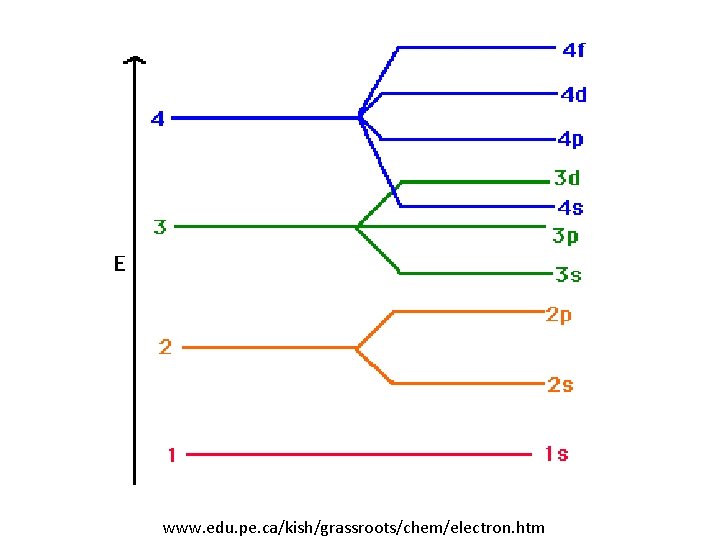
www. edu. pe. ca/kish/grassroots/chem/electron. htm


Key Points • Pauli exclusion principle: no two electrons in an interacting systems can have the exact same set of quantum numbers • They can’t have exactly the same energies (except for spin) – Causes states to split slightly (hyperfine splitting) – Number of split states equal to number of atoms (e. g. two in the H 2 molecule • Next up: apply this knowledge to a crystal – Covalent bonding in crystalline solids

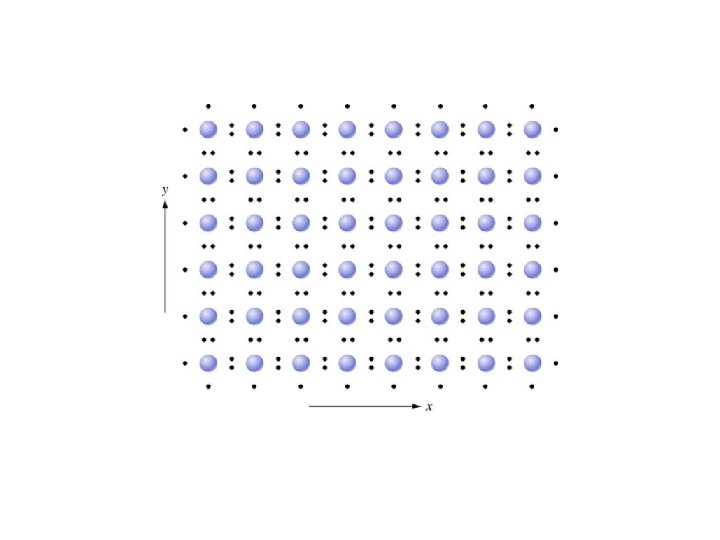
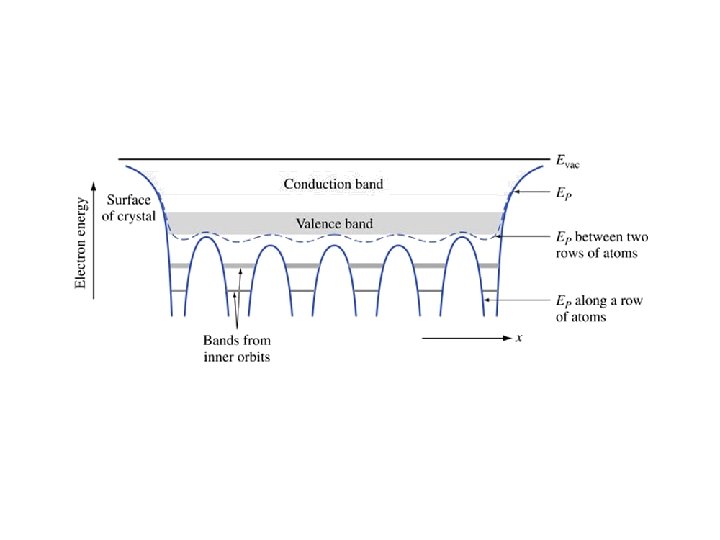
Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Covalent Bonding in Crystalline Solids Chapter 1 Section 3. 4 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display






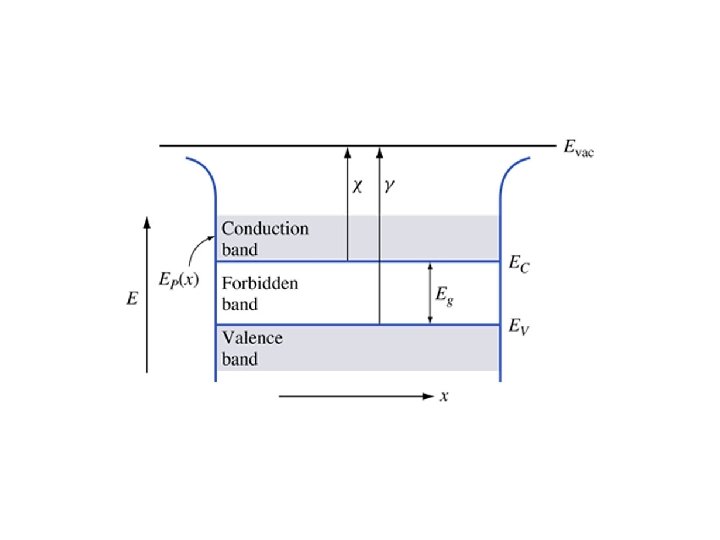
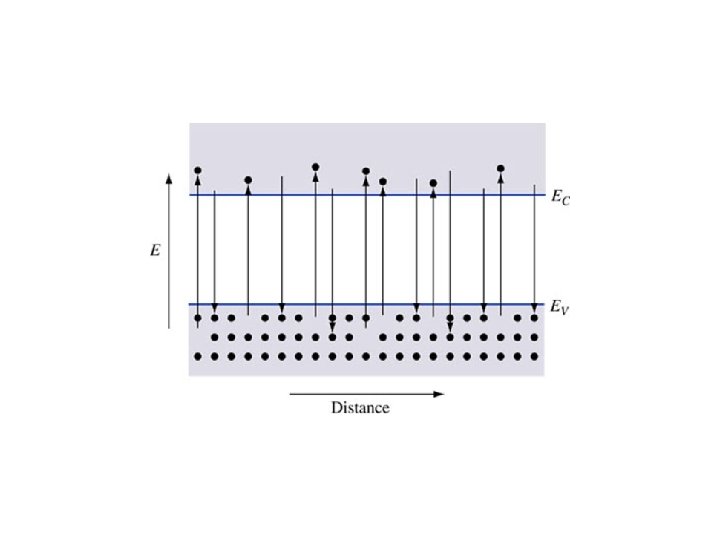
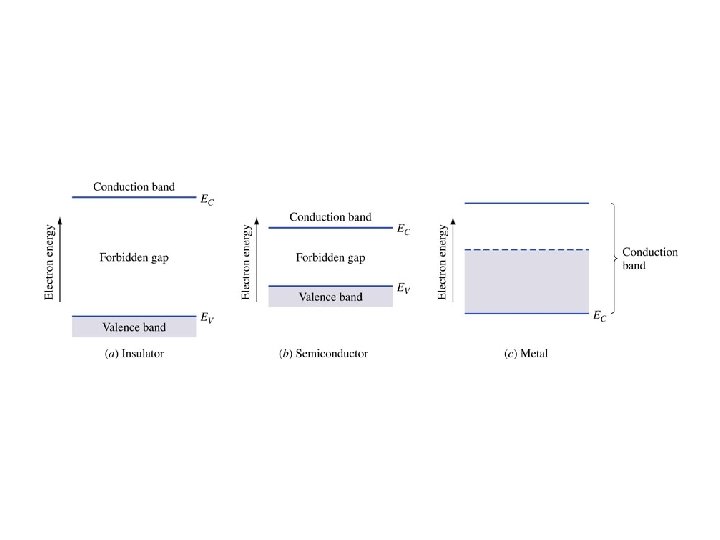
At absolute zero (0 Kelvins), every electron is in the lowest possible energy state. • In a perfect semiconductor, every state in the valence band is occupied by an electron and every state in the conduction band is empty.



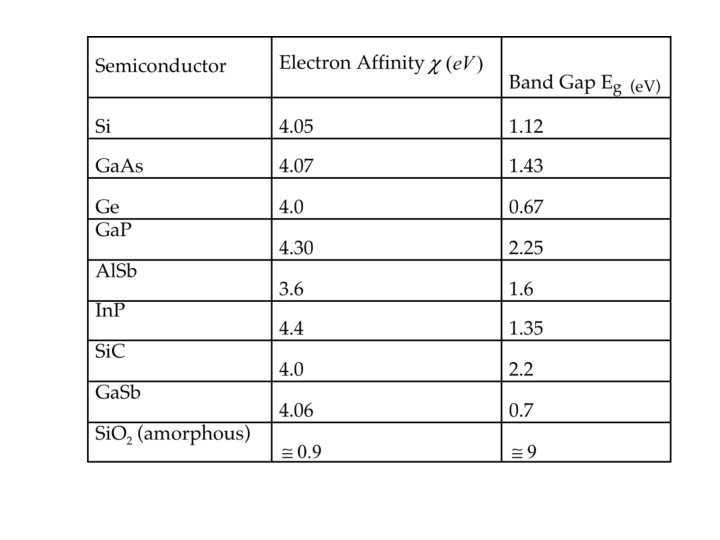
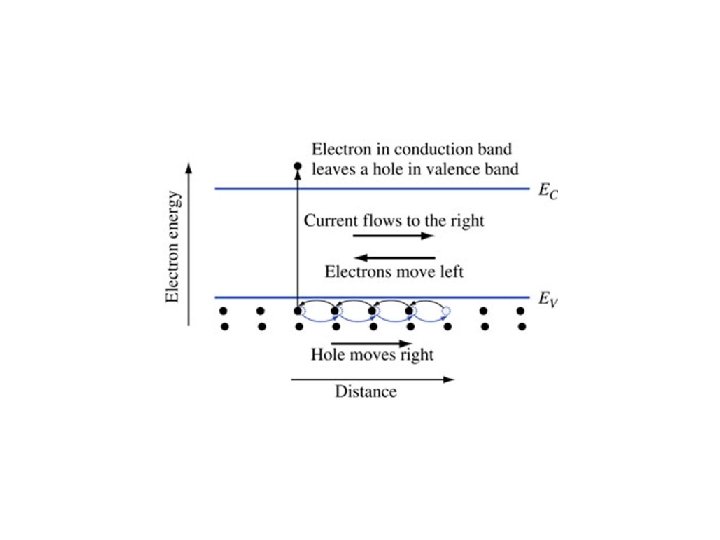
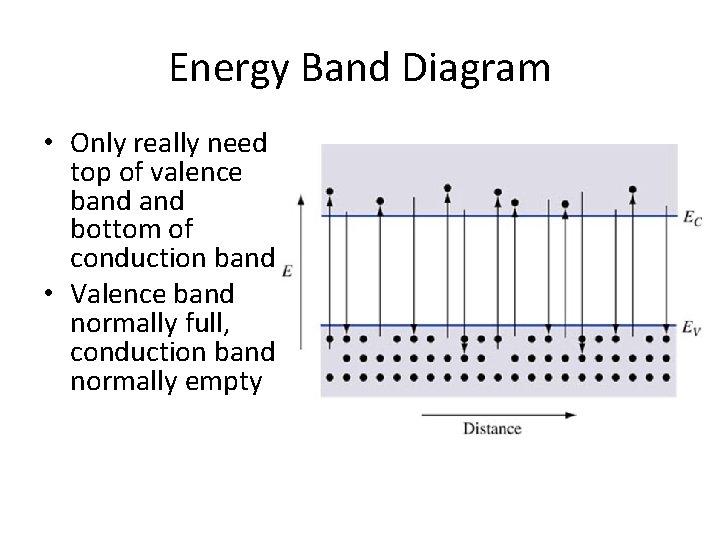
Key Points • Electrons in the valence band hold the crystal together • Electrons in the conduction band are free to move around the crystal • Each material has a specific – Electron affinity : difference between Evac and EC – Ionization energy : difference between Evac and EV – Band gap Eg: difference between EC and EV • At 0 K, all states in VB are full and all states in CB are empty • Above 0 K, electrons in the CB can move and conduct electricity; holes in the VB can conduct electricity

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Wave Particle Duality Chapter 1 Section 4 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Classical waves • Have energies that are quantized – Electromagnetic waves: energy quantum is a photon – Acoustic waves: phonon

Consider an electromagnetic wave • E is the electric field • K is the wavenumber • λ is the wavelength • ν is the frequency • ω is the angular frequency

Classical particles • Can be considered to be • Matter wave: waves – Have energy – Have wavelength • Actual matter particles have mass – E. g. electron • Wavelength, as before • K is still wavenumber

Matter wave • Matter wave: • BUT! Ψ is NOT mass • It is called the “wavefunction” • It actually has no direct physical meaning

Usually written • Exponential form • This form is for an electron in vacuum (free space- will have to modify it for electrons in a material.

Key Points • There are waves and there are particles • Objects such as electrons can be described either way – One isn’t right and the other wrong – Pick the description that is most convenient for the problem you’re solving • Electron matter wave described by a wavefunction ψ – Wavefunction ψ doesn’t have direct physical meaning- but is still very useful! Stay tuned. – Still has wavenumber – Energy of the particle appears in the equation

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Wave Function Chapter 1 Section 5 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Recall the wave function • We said it could represent a particle – Matter wave such as an electron – This is the wave function for an electron in free space: looks like a plane wave • Quantity has no direct physical meaning • Will see value of it shortly

In three dimensions • We’ll use 1 -D version whenever possible

Probability and the wave function • Probability density P • Probability that a particle is found in region dx at a time t is given by

Example: electron in free space (vacuum)

To find probability of being in some “place” • Integrate both sides over the part of space you’re interested in – What is the probability the electron is in this box? – Integrate over the box • Electron has to be somewhere! – Integrate over all space, result has to be 1 – In this case the wavefunction is said to be normalized

Key points • Wave function has no direct physical meaning • BUT! is a probability density function • We can use this information to find out things about the electron

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Electron Wave Function Chapter 1 Section 6 Introduction Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Recall the wave function • Let’s break it up into to time- and spacedependent parts • Remember, E is the particle’s energy

But how do you find ? • You solve Schroedinger’s Equation – We’ll explain this in detail in Supplement to Part I • Synopsis: Time-independent Schroedinger’s Equation

Key points • Solve Schroedinger’s equation for the problem you want to solve – The problem you’re solving is described by the potential energy EP • Once you find ψ you can find the particle’s probability density function – From there can find out things about the particle (we haven’t covered yet)

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Free Electron in One Dimension Chapter 1 Section 6. 1 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display


Time-independent Schroedinger’s Equation For us, inside crystal, not near the edges,

To solve: General Solutions: Of the form: For us:

Total solution, putting back in the time dependence: Two plane waves, one propagating in +x direction, other in –x direction Need to talk about K, and need to talk about

Key points • To find the wave function, solve Shroedinger’s equation – Problem you’re solving described by EP • In this case (free electron) potential constant everywhere • Result was two plane waves • Part B: physical interpretation

Solution: Given: Phase velocity Group velocity Not unique, because E depends on potential energy reference Unique.

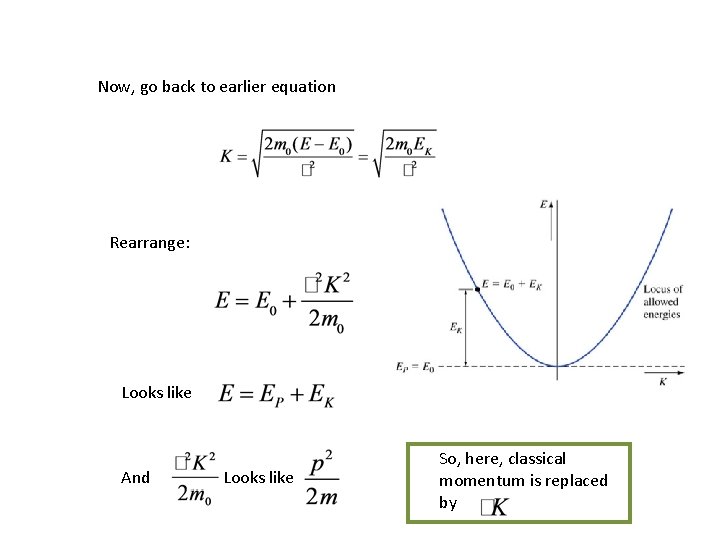
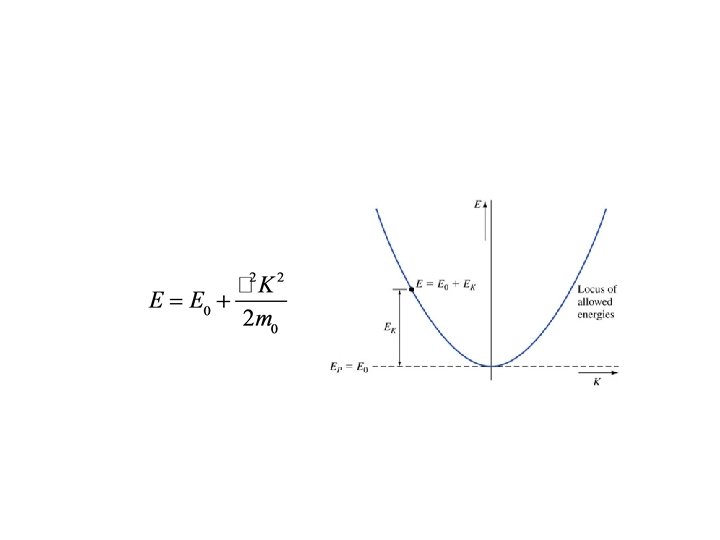
Now, go back to earlier equation Rearrange: Looks like And Looks like So, here, classical momentum is replaced by


Key points • To find the wave function, describe the physical problem using EP • We modeled the free electron in a region of constant potential • Solution was plane waves in x! • Guess matter really is a wave… • But cannot be interpreted as angular frequency because E has an arbitrary reference • Classical momentum is replaced by

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The de Broglie Relationship Chapter 1 Section 6. 2 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Wave, particle: Connection? Repeats whenever Therefore increases by one wavelength every n, or

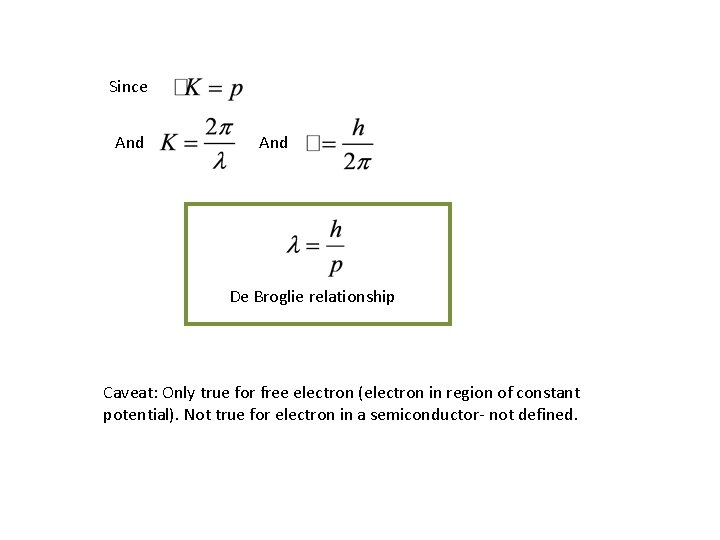
Next, take derivative of And recall that the group velocity Wow! For the free electron, anyway, really is the momentum!

Since And De Broglie relationship Caveat: Only true for free electron (electron in region of constant potential). Not true for electron in a semiconductor- not defined.

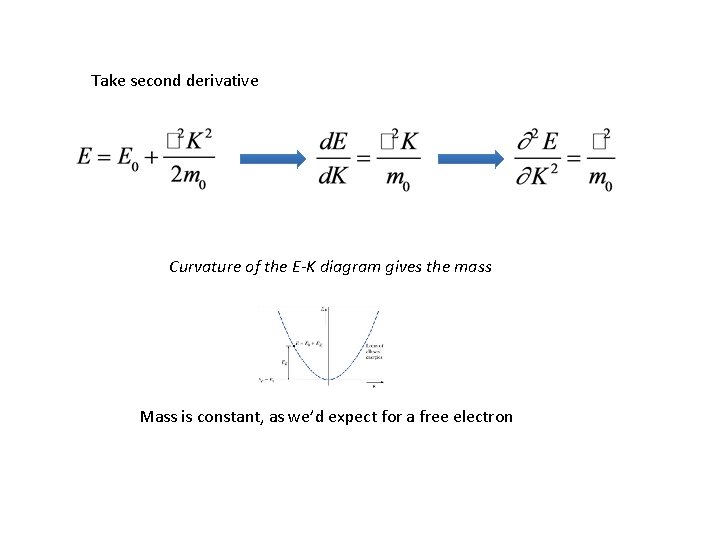
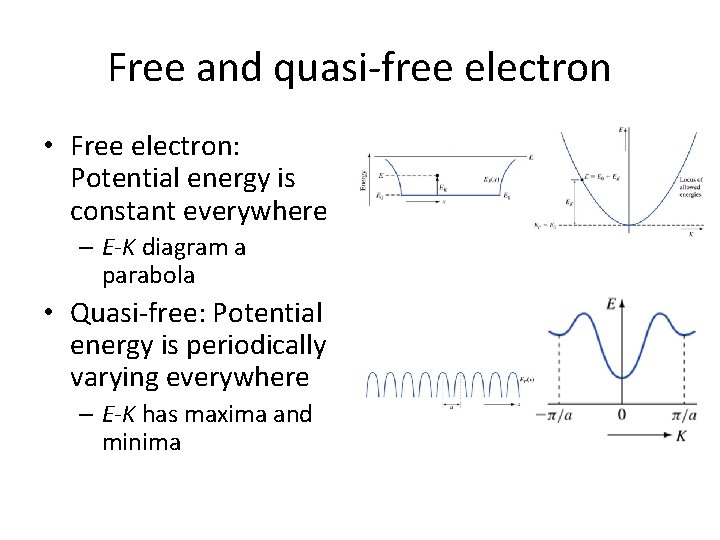
Take second derivative Curvature of the E-K diagram gives the mass Mass is constant, as we’d expect for a free electron

Key points • We used the wavefunction for the electron in a region of constant potential (free electron) • Took derivative of – Compared to equation for group velocity – Found momentum was – Found a wavelength • Took second derivative – Found mass from curvature of E-K diagram • Remember: de Broglie wavelength defined only for an electron in a region of constant potential

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Free Electron in Three Dimensions Chapter 1 Section 6. 3 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

If EP is constant everywhere in three dimensions: where

Key points • There is one allowed energy "band"– the range of energies between E 0 and infinity represents the allowed energy states for the free electron. – The energy band has a minimum at E=E 0, K=0. • The velocity of the electron in a given direction is given by

More key points • The E-K relation is a paraboloid in three dimensions – The curvature of the paraboloid is given by its second derivative – For the free electron, E 0 is constant everywhere, so the curvature of the E-K curve is the same in any direction in Kspace – Thus mass is a constant for the free electron • De Broglie's relation λ =h/p is valid for this case, and p=mv

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Quasi-Free Electron Model Chapter 1 Section 6. 4 PART A Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Where we’ve been • We found the wave function for a free electron – Put a constant potential energy into Schroedinger’s equation and solved it – Found E as a function K – Found group velocity from derivative – Found mass related to curvature

Where we’re going • We’ll try the same thing for an electron in an infinite periodic potential – Like in a semiconductor crystal – We’ll put periodic EP into S. E. and solve – Draw conclusions about velocity and mass – This problem is hard so we’re going to cheat and use the Bloch theorem

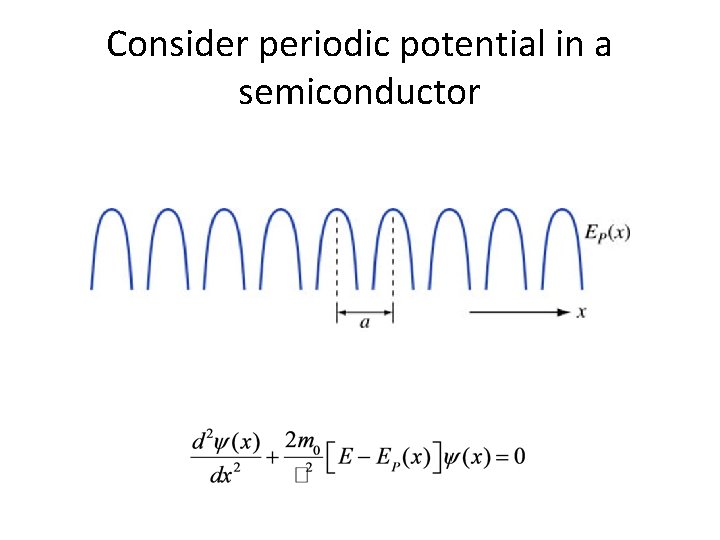
Consider periodic potential in a semiconductor

We don’t actually know Bloch theorem: for an electron in a periodic potential, the time-independent wave function is Where UK(x) is some function that is • Periodic in x • Has the same periodicity as the crystal

• Plane wave • Modulated by some periodic function UK(x) with period a of the crystal • Since it is periodic,

Don’t know what UK(x) looks like, but • We know that the crystalline forces acting on the electron are independent of the direction of propagation • This means E(K) has an extremum at K=0

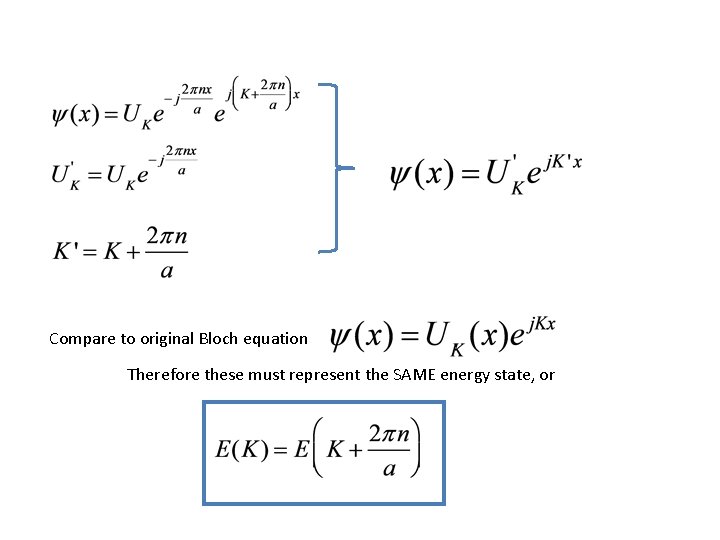
Multiply Define: by

Compare to original Bloch equation Therefore these must represent the SAME energy state, or

Key points: We know the potential energy is periodic We don’t know what it looks like We do know the Bloch theorem Result is that the E-K relationship is periodic in K • In next part, we’ll interpret what that means physically. • •

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill The Quasi-Free Electron Model Chapter 1 Section 6. 4 PART B Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

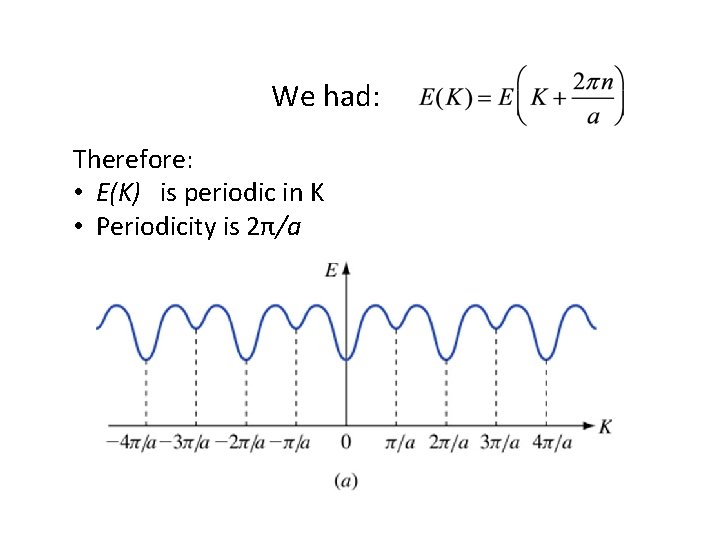
We had: Therefore: • E(K) is periodic in K • Periodicity is 2π/a


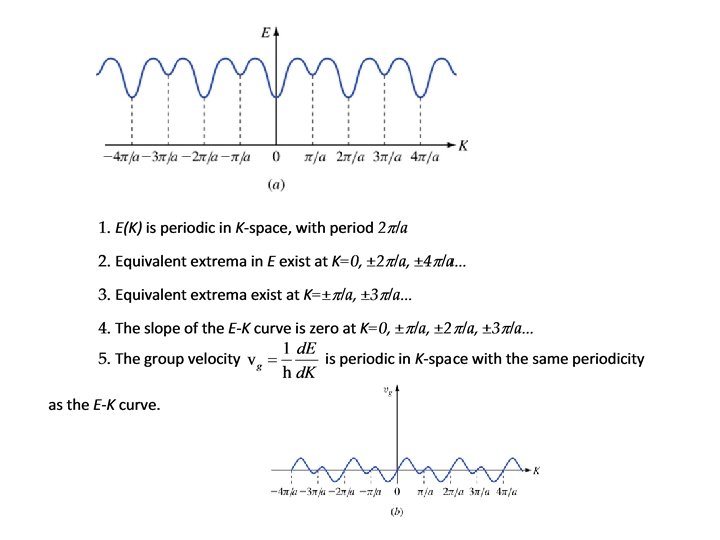
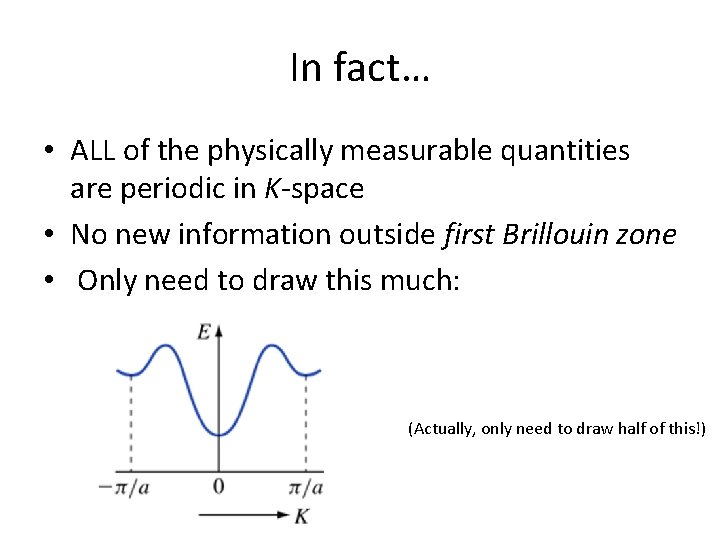
In fact… • ALL of the physically measurable quantities are periodic in K-space • No new information outside first Brillouin zone • Only need to draw this much: (Actually, only need to draw half of this!)

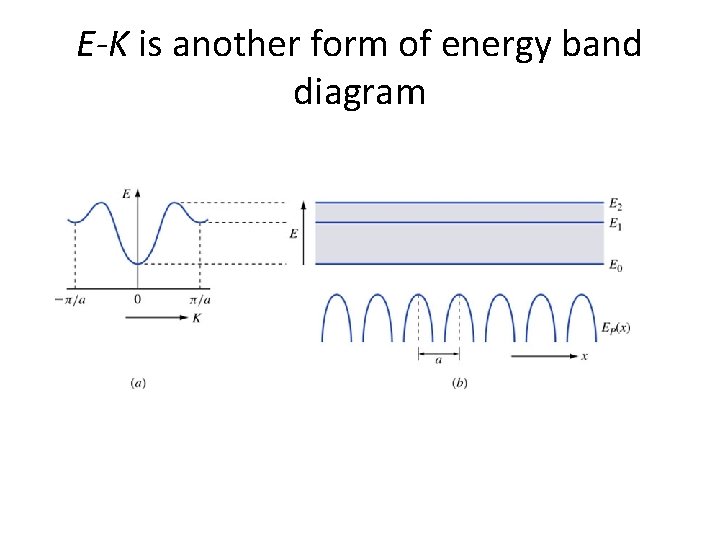
E-K is another form of energy band diagram

Compare to free electron results • as before, but now • We didn’t know anything about EP(x) except it was periodic, so we don’t know anything more about K here

What about momentum? • For free electron, • In crystal, de Broglie relationship does not hold • Therefore, is NOT momentum • But is analogous to classical momentum – Sometimes called crystal momentum

Quasi free electron in 3 D • EP(r) is periodic in all crystallographic directions • And UK(r) has the same periodicity as EP(r) and

We ignored the edges of the crystal • In free electron an quasi-free electron we neglected any edges – Electron could not reflect back from an edge – Single Bloch wave sufficient • In real crystal mean free path is ≈nm, so must consider collisions – Real wave function must be superposition of wave functions – We’ll take this up in Supplement A to Part 1 Quantum Mechanics

Key points • Considered electron in infinite periodic potential – Didn’t know what potential is, just that it’s periodic – Used Bloch Theorem which says that wave function is periodic – Showed that E-K is periodic in K – Group velocity was also periodic • As as all measureable quantities – Only need to draw first Brillouin zone

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Reflection and Tunneling Chapter 1 Section 6. 5 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

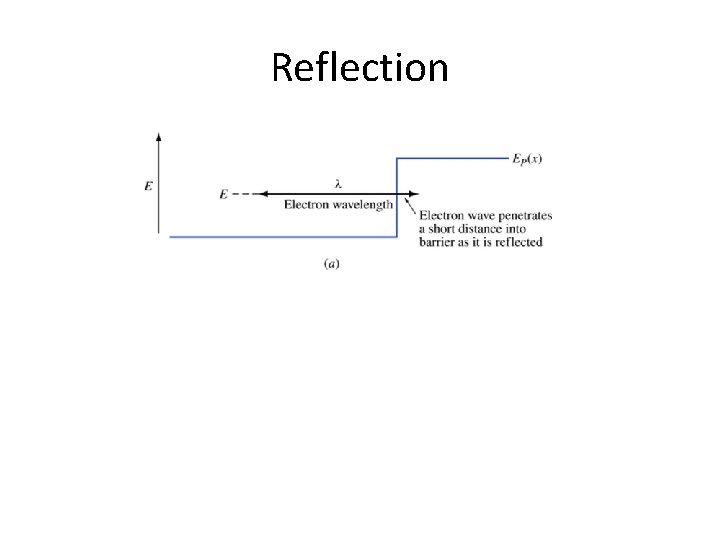
Some wave-like behavior • Sometimes convenient to think of electrons as particles • Sometimes electrons (and any particles) do some wave-like things • Examples: – Reflection from a potential barrier – Tunneling

Reflection

Tunneling

Key points • Particles have wave-like behavior • They can tunnel through barriers – Probability increases as barrier gets thinner – Probability can be non-negligible – Tunneling widely used in semiconductor devices • We will see more of this as we go along – Of particular interest: • Supplement A to Part 1: Quantum Mechanics

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill A First Look at Optical Emission and Absorption Chapter 1 Section 7 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Particle behavior of light • Sometimes convenient to think of light as a wave • Sometimes light does some particle-like things • Light can be thought of as consisting of particles: photons • Energy must be absorbed or emitted in these quanta n= frequency

What is the energy of a red photon? • Let λ=600 nm (red light)

Example 1. 3 An electron in a hydrogen atom can switch from one allowed energy level to another by either absorbing or emitting energy. Scientists use the spectra of the light emitted by various materials to determine their energy structure. For each of the following spectral lines, determine the initial and final energy states. a) λ 1=656. 28 nm (red) Recall energies of hydrogen atom from the Bohr model

We had Recall energies of hydrogen atom from the Bohr model: try some combinations

Example 1. 3 continued • Blue light of λ=486. 13 nm • Violet light of λ=435. 05 nm

What energy level do they all have in common? • Balmer series of transitions involve Level 2 • Lyman series involve Level 1 • Paschen series involve Level 3

Energy of a light beam • The energy of a photon depends on the wavelength of the light • If you want a more powerful beam of that color, need more photons per second

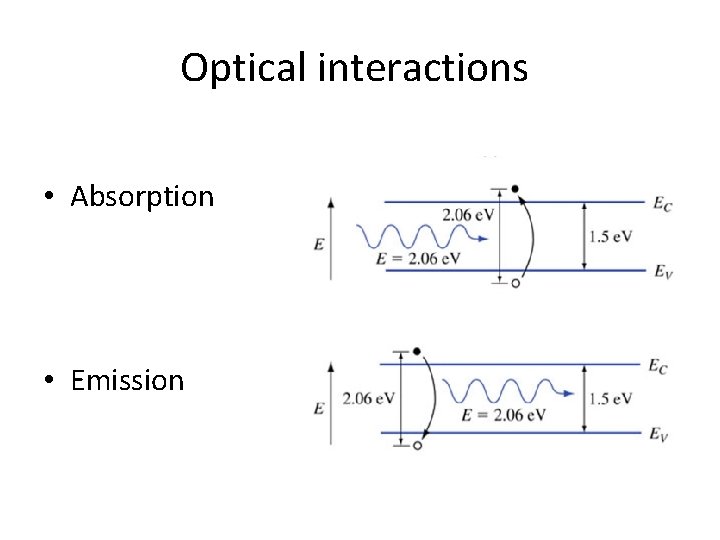
Absorption and emission in a semiconductor • Transparent • Absorption • Emission Energy must be conserved!

Example 1. 4 Light of 100 μW is incident on a photodetector. (a) If the light is green (500 nm), how many photons are striking the surface per second? This is the energy per photon.

Power is energy per time

What if light is infrared? If the power remains at 100μW, but the wavelength of the light is changed to infrared (λ=1μm), now how many photons strike the surface per second? Green Infrared 2. 47 e. V 1. 25 e. V 2. 54 x 1014 photons/sec 5. 05 x 1014 photons/sec

GOLDEN RULE

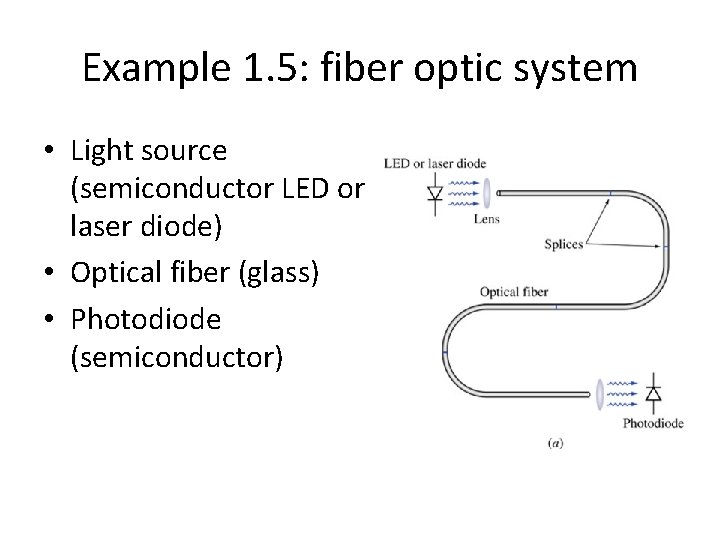
Example 1. 5: fiber optic system • Light source (semiconductor LED or laser diode) • Optical fiber (glass) • Photodiode (semiconductor)

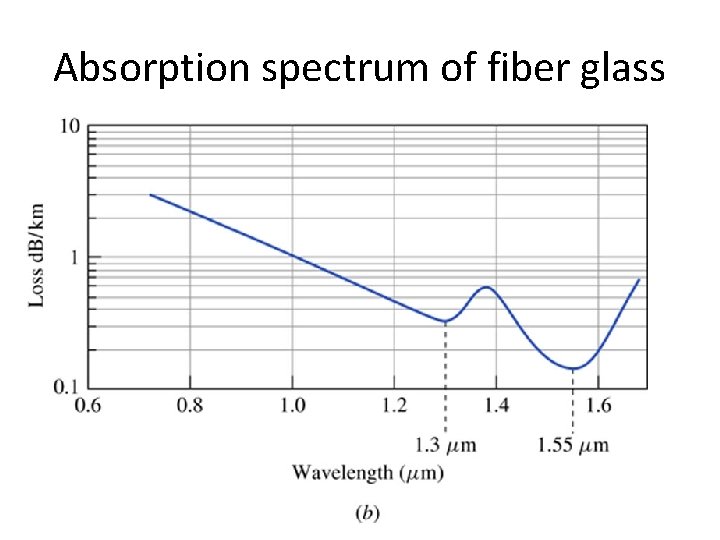
Absorption spectrum of fiber glass

For LED to emit at 1. 55 μm… • What should band gap of semiconductor be? – Apply Golden Rule • Bandgap of photodiode? – 0. 8 e. V

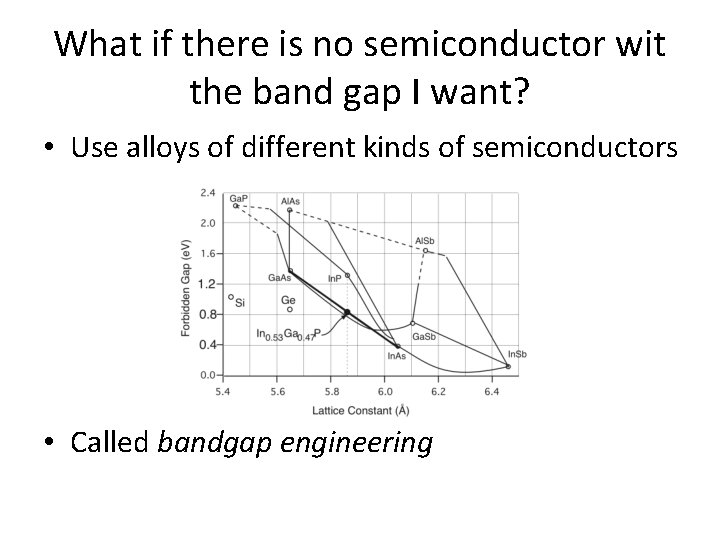
What if there is no semiconductor wit the band gap I want? • Use alloys of different kinds of semiconductors • Called bandgap engineering

Key points • Light comes in photons of a specific energy that depends on the wavelength • Light can only be absorbed or emitted in integer multiples of these quanta • To deliver more power, deliver more photons

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Crystal Structures, Planes, and Directions Chapter 1 Section 8 Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Why crystallography? • Silicon, Ga. As, In. P, etc. are crystals • Important to understand arrangement of atoms – To understand electrical properties – To understand chemical properties for fabrication

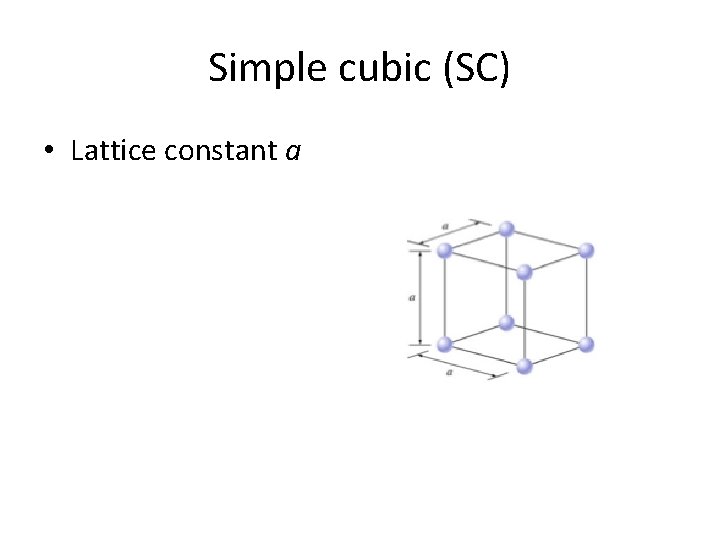
Simple cubic (SC) • Lattice constant a

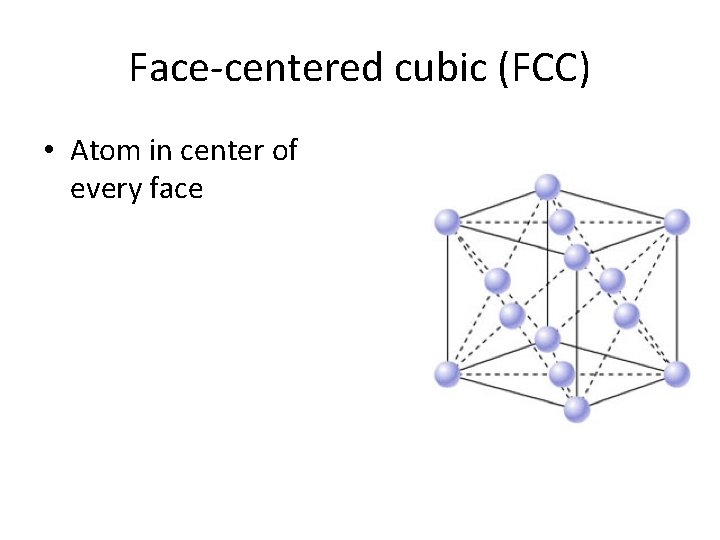
Face-centered cubic (FCC) • Atom in center of every face

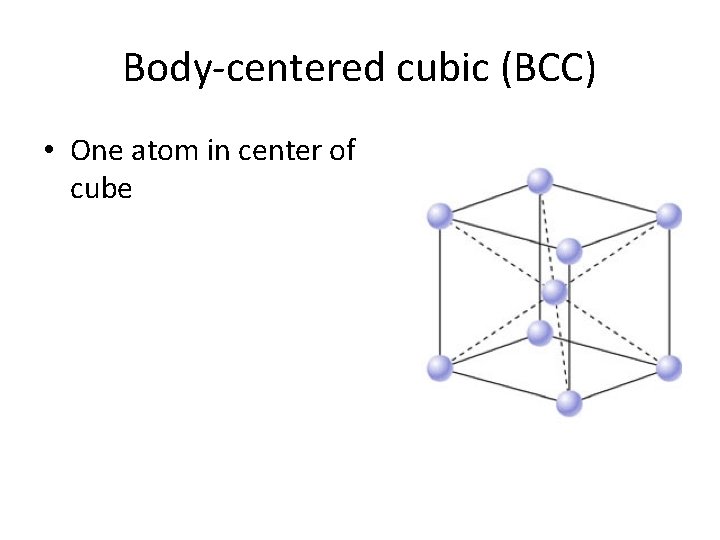
Body-centered cubic (BCC) • One atom in center of cube

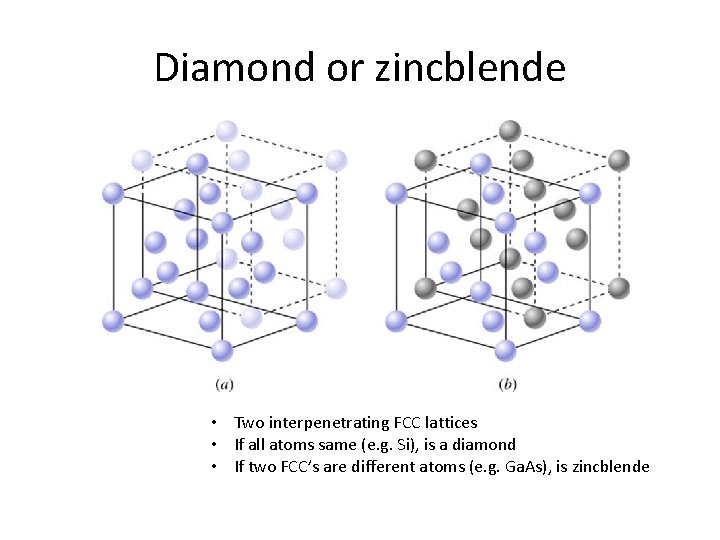
Diamond or zincblende • Two interpenetrating FCC lattices • If all atoms same (e. g. Si), is a diamond • If two FCC’s are different atoms (e. g. Ga. As), is zincblende

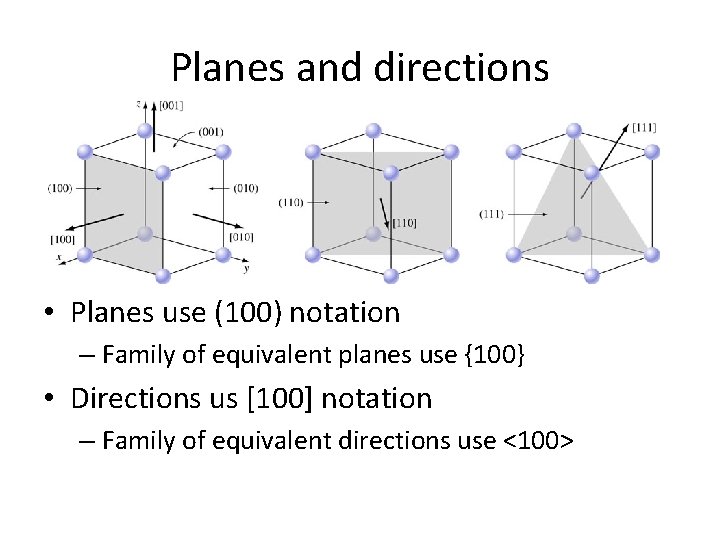
Planes and directions • Planes use (100) notation – Family of equivalent planes use {100} • Directions us [100] notation – Family of equivalent directions use <100>

Key points • Crystal structure will affect periodic potential – Therefore affects electrical properties – Also affects optical properties • Diamond lattice is common in semiconductors – Consists of two interpenetrating FCC lattices – Compound semiconductors often have zincblende structure • Crystal planes and directions important for discussing electrical and chemical properties

Fundamentals of Semiconductor Devices Anderson and Anderson Mc. Graw-Hill Chapter 1 Section 9 Summary Copyright © 2016 The Mc. Graw-Hill Companies, Inc. Permission required for presentation or display

Bohr model • Electrons orbit around nucleus • Centripetal force=centrifugal force • Integral of angular momentum around one orbit is integer multiple of h • Result was discrete energy levels • We did this for a hydrogen atom • Considered effect of shared electrons in covalent bonding

Pauli Exclusion Principle • No two electrons in an interacting system can have the exact same set of quantum numbers. • Resulted in energy bands in a crystal • Some levels not shared across crystal • Valence band contains the electrons holding the crystal together • Conduction band contains electrons that can travel around crystal easily

Energy Band Diagram • Only really need top of valence band bottom of conduction band • Valence band normally full, conduction band normally empty

Wave-particle duality • Electrons and photons can be considered as either particles or waves – Whichever is most convenient at the time • Electrons have a wave function – Found by solving Schroedinger’s equation – Can be used to determine probability of finding an electron in a given region – Results in an E-K diagram where K is the wave vector

Free and quasi-free electron • Free electron: Potential energy is constant everywhere – E-K diagram a parabola • Quasi-free: Potential energy is periodically varying everywhere – E-K has maxima and minima

Optical interactions • Absorption • Emission

Coming up • More on interpreting E-K diagrams • More on band structure • Movement of electrons to generate current
 Fundamentals of semiconductors
Fundamentals of semiconductors Zerobioelectronic
Zerobioelectronic Advanced semiconductor fundamentals
Advanced semiconductor fundamentals Advanced semiconductor fundamentals
Advanced semiconductor fundamentals Ee 130
Ee 130 Semiconductor device fundamentals
Semiconductor device fundamentals Dispositivos de 4 capas
Dispositivos de 4 capas Johanna müting
Johanna müting Special semiconductor devices
Special semiconductor devices Classification of power semiconductor devices
Classification of power semiconductor devices Semiconductor devices
Semiconductor devices Power semiconductor devices lecture notes
Power semiconductor devices lecture notes Intro to semiconductors
Intro to semiconductors Electronics fundamentals circuits devices and applications
Electronics fundamentals circuits devices and applications Literary elements and techniques examples
Literary elements and techniques examples Computer system input
Computer system input Drift current and diffusion current
Drift current and diffusion current Drift current
Drift current Drift current and diffusion current
Drift current and diffusion current Energy band in conductor semiconductor and insulator
Energy band in conductor semiconductor and insulator Diffusion current formula
Diffusion current formula Advantages and disadvantages of semiconductor detector
Advantages and disadvantages of semiconductor detector Journal of semiconductor technology and science
Journal of semiconductor technology and science Backgrinding process
Backgrinding process Semiconductor laser principle
Semiconductor laser principle Types of semiconductor in physics
Types of semiconductor in physics Heat and mass transfer fundamentals and applications
Heat and mass transfer fundamentals and applications Pn junction diode and zener diode difference
Pn junction diode and zener diode difference Semiconductor ram memories
Semiconductor ram memories Semiconductor tipo p
Semiconductor tipo p Carbon dioxide temperature
Carbon dioxide temperature Disadvantages of semiconductor detector
Disadvantages of semiconductor detector Semiconductor industry association sia
Semiconductor industry association sia Semiconductor curve tracer
Semiconductor curve tracer Runtomrun
Runtomrun Semiconductor industry structure
Semiconductor industry structure Compound semiconductor week
Compound semiconductor week National semiconductor adc 0801 menggunakan prinsip
National semiconductor adc 0801 menggunakan prinsip Compound semiconductor magazine
Compound semiconductor magazine Intrinsic carrier concentration
Intrinsic carrier concentration Continuity equation in semiconductor
Continuity equation in semiconductor Continuity equation
Continuity equation Continuity equation derivation in semiconductors
Continuity equation derivation in semiconductors Semiconductor definition physics
Semiconductor definition physics Impurezas aceptoras
Impurezas aceptoras Semiconductor ip company
Semiconductor ip company Hong xiao semiconductor
Hong xiao semiconductor Intrinsic semiconductor
Intrinsic semiconductor National semiconductor adc 0801 menggunakan prinsip
National semiconductor adc 0801 menggunakan prinsip Ceramic semiconductor thermometer
Ceramic semiconductor thermometer Memory expansion in digital electronics
Memory expansion in digital electronics Ge diode
Ge diode Intrinsic semiconductor carrier concentration
Intrinsic semiconductor carrier concentration Semiconductor history timeline
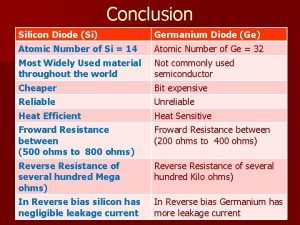
Semiconductor history timeline Diode conclusion
Diode conclusion Define semiconductor
Define semiconductor Wigner seitz cell of fcc
Wigner seitz cell of fcc Semiconductor engineering physics
Semiconductor engineering physics Metal semiconductor field effect transistor
Metal semiconductor field effect transistor Intrinsic vs extrinsic semiconductor
Intrinsic vs extrinsic semiconductor Intrinsic carrier density
Intrinsic carrier density Carrier concentration in intrinsic semiconductor
Carrier concentration in intrinsic semiconductor Carrier concentration in intrinsic semiconductor
Carrier concentration in intrinsic semiconductor Internal organization of memory chips
Internal organization of memory chips Calister
Calister Semiconductor definition
Semiconductor definition Junction semiconductor detector
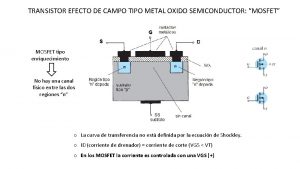
Junction semiconductor detector Transistor de efecto de campo metal-óxido-semiconductor
Transistor de efecto de campo metal-óxido-semiconductor Semiconductor
Semiconductor Ohmic contact
Ohmic contact Semiconductor device fabrication
Semiconductor device fabrication Pfc semiconductor
Pfc semiconductor Continuity equation of semiconductor
Continuity equation of semiconductor Mos capacitor band diagram
Mos capacitor band diagram Dr jeremy wang
Dr jeremy wang Semiconductor packaging materials
Semiconductor packaging materials Semiconductor complex chandigarh
Semiconductor complex chandigarh Dmt 234
Dmt 234 Dmt 234
Dmt 234 Công ty seoul semiconductor vina
Công ty seoul semiconductor vina Carrier concentration equation
Carrier concentration equation Atomic structure of semiconductor
Atomic structure of semiconductor Nassi-schneiderman
Nassi-schneiderman Polishing head
Polishing head Semiconductor
Semiconductor Dc physics
Dc physics Od semiconductor
Od semiconductor What does a semiconductor look like
What does a semiconductor look like Internal memory rom
Internal memory rom Seoul semiconductor vina co. ltd
Seoul semiconductor vina co. ltd Darlington kapcsolás
Darlington kapcsolás Semiconductor
Semiconductor Advanced dram organization
Advanced dram organization Budijanto chandra
Budijanto chandra Semiconductor detector
Semiconductor detector State law of mass action
State law of mass action Hall effect experiment
Hall effect experiment Semiconductor
Semiconductor Metal oxide semiconductor field effect transistor
Metal oxide semiconductor field effect transistor Semiconductor
Semiconductor International roadmap for semiconductors
International roadmap for semiconductors Simat wafer
Simat wafer Semiconductor
Semiconductor E-k diagram
E-k diagram Semiconductor
Semiconductor Nhanced semiconductor
Nhanced semiconductor Drift current in semiconductor
Drift current in semiconductor Derive fermi dirac distribution law
Derive fermi dirac distribution law Poisson's equation
Poisson's equation Semiconductor materials
Semiconductor materials Curva caracteristica del diodo de potencia
Curva caracteristica del diodo de potencia Semiconductor
Semiconductor Semiconductor industry association
Semiconductor industry association Conductivity of intrinsic semiconductor formula
Conductivity of intrinsic semiconductor formula Tsmc semiconductor
Tsmc semiconductor Ram types comparison
Ram types comparison Semiconductor technology roadmap
Semiconductor technology roadmap Regiones de trabajo de un transistor
Regiones de trabajo de un transistor Vad är halvledare
Vad är halvledare Sm sze
Sm sze International technology roadmap for semiconductors
International technology roadmap for semiconductors Anderson and mcfarlane community assessment wheel
Anderson and mcfarlane community assessment wheel The anderson school gifted and talented nyc
The anderson school gifted and talented nyc Bartholow and anderson 2002
Bartholow and anderson 2002 Mta security fundamentals exam questions
Mta security fundamentals exam questions Logic and computer design fundamentals
Logic and computer design fundamentals Jk flip flop
Jk flip flop 010000112
010000112 Logic and computer design fundamentals
Logic and computer design fundamentals Activity and exercise fundamentals of nursing
Activity and exercise fundamentals of nursing Tire wheel and wheel bearing fundamentals
Tire wheel and wheel bearing fundamentals Tire wheel and wheel bearing fundamentals
Tire wheel and wheel bearing fundamentals Fundamentals of data and signals
Fundamentals of data and signals Understanding your health and wellness
Understanding your health and wellness Customer service and sales fundamentals
Customer service and sales fundamentals Fundamentals of nursing chapter 16
Fundamentals of nursing chapter 16 Neuron process
Neuron process Fluid mechanics fundamentals and applications 3rd edition
Fluid mechanics fundamentals and applications 3rd edition Database processing fundamentals design and implementation
Database processing fundamentals design and implementation Productivity output input
Productivity output input Process instrumentation ppt
Process instrumentation ppt Fundamentals of planning and developing tourism
Fundamentals of planning and developing tourism Fundamentals of data and signals
Fundamentals of data and signals Forensic science fundamentals and investigations chapter 6
Forensic science fundamentals and investigations chapter 6 Introduction to futures and options
Introduction to futures and options Applications of plasmonics
Applications of plasmonics Fundamentals of food service operation
Fundamentals of food service operation Understanding health and wellness
Understanding health and wellness Evolution and fundamentals of business
Evolution and fundamentals of business Pain definition nursing
Pain definition nursing Thermal resistance formula
Thermal resistance formula