Fundamentals of Normal Metal and Superconductor Electrodynamics Steven

Fundamentals of Normal Metal and Superconductor Electrodynamics Steven M. Anlage Center for Nanophysics and Advanced Materials Physics Department University of Maryland College Park, MD 20742 -4111 USA anlage@umd. edu 1

Outline • High Frequency Electrodynamics of Superconductors • Experimental High Frequency Superconductivity • Further Reading 2

The Three Hallmarks of Superconductivity Zero Resistance Complete Diamagnetism Macroscopic Quantum Effects Flux F V 0 Tc Temperature Magnetic Induction DC Resistance I T>Tc 0 T<Tc Flux quantization F = n. F 0 Josephson Effects Tc Temperature 3

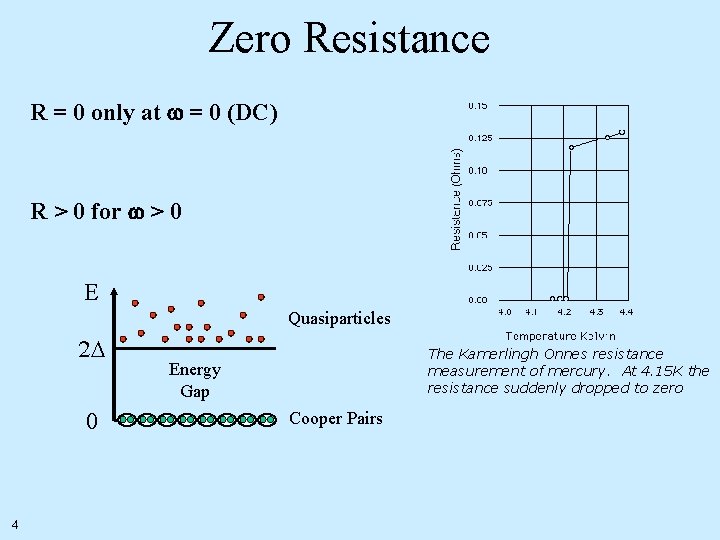
Zero Resistance R = 0 only at = 0 (DC) R > 0 for > 0 E Quasiparticles 2 D 0 The Kamerlingh Onnes resistance measurement of mercury. At 4. 15 K the resistance suddenly dropped to zero Energy Gap Cooper Pairs 4

Perfect Diamagnetism Magnetic Fields and Superconductors are not generally compatible The Meissner Effect Superconductor l(T) magnetic penetration depth T>Tc vacuum l superconductor surface screening currents l(0) T Tc The Yamanashi MLX 01 Mag. Lev test vehicle achieved a speed of 361 mph (581 kph) in 2003 5 Spontaneous exclusion of magnetic flux B=0 l l is independent of frequency (w < 2 D) T<Tc

High Frequency Electrodynamics of Superconductors • Why are Superconductors so Useful at High Frequencies? • Normal Metal Electrodynamics • The Two-Fluid Model • London Equations • BCS Electrodynamics • Nonlinear Surface Impedance 6

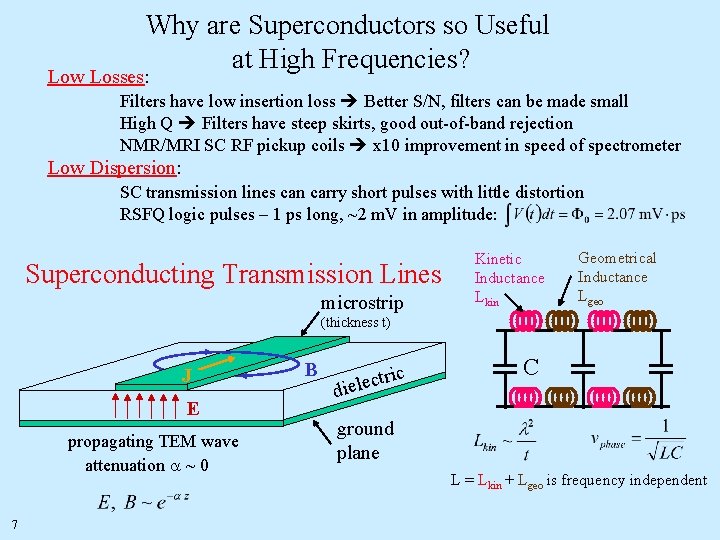
Why are Superconductors so Useful at High Frequencies? Low Losses: Filters have low insertion loss Better S/N, filters can be made small High Q Filters have steep skirts, good out-of-band rejection NMR/MRI SC RF pickup coils x 10 improvement in speed of spectrometer Low Dispersion: SC transmission lines can carry short pulses with little distortion RSFQ logic pulses – 1 ps long, ~2 m. V in amplitude: Superconducting Transmission Lines microstrip Kinetic Inductance Lkin Geometrical Inductance Lgeo (thickness t) J E propagating TEM wave attenuation a ~ 0 B ric t c e l die ground plane L = Lkin + Lgeo is frequency independent 7 C

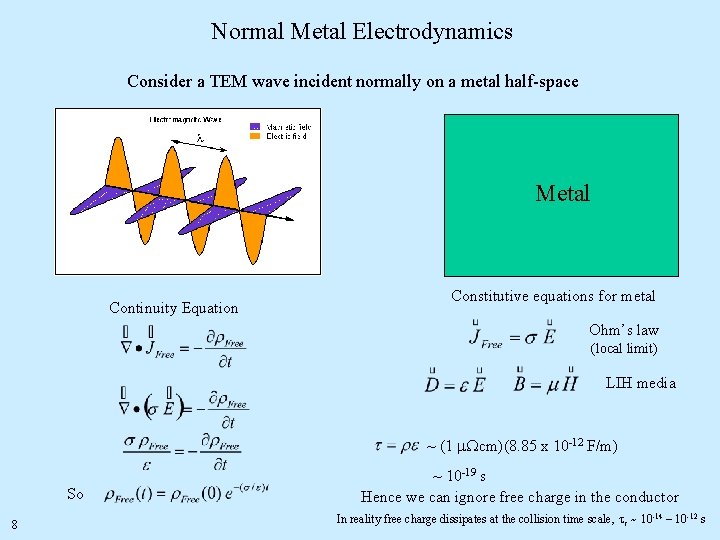
Normal Metal Electrodynamics Consider a TEM wave incident normally on a metal half-space Metal Continuity Equation Constitutive equations for metal Ohm’s law (local limit) LIH media ~ (1 m. Wcm)(8. 85 x 10 -12 F/m) So 8 ~ 10 -19 s Hence we can ignore free charge in the conductor In reality free charge dissipates at the collision time scale, tc ~ 10 -14 – 10 -12 s

Normal Metal Electrodynamics Take the curl of the curl equations These are wave equations with a ms dissipative term Ansatz with One finds The waves oscillate and decay as they enter the metal Define the skin depth 9 For a metal with r = 1 m. W-cm at 2. 5 GHz,

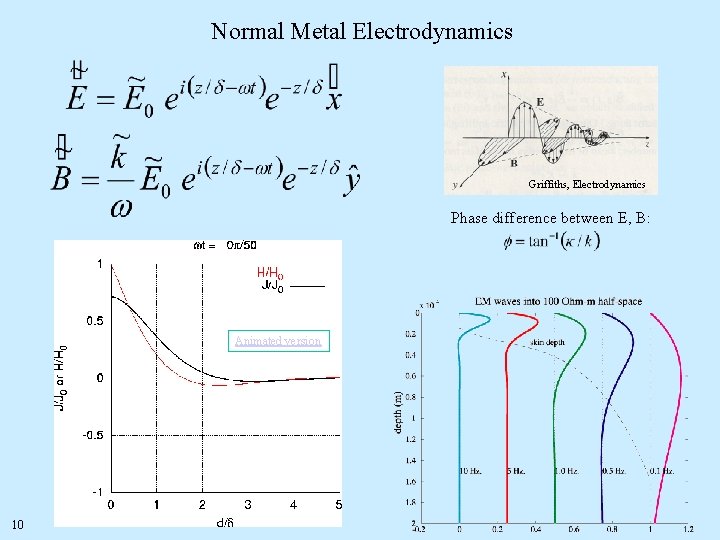
Normal Metal Electrodynamics Griffiths, Electrodynamics Phase difference between E, B: Animated version 10

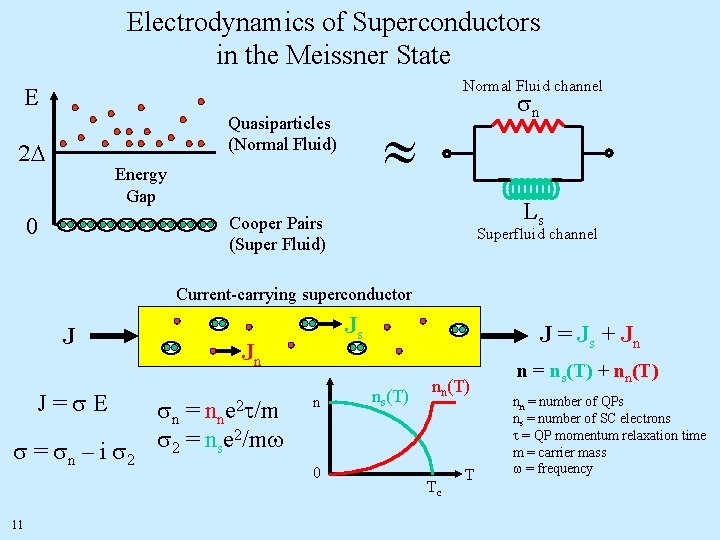
Electrodynamics of Superconductors in the Meissner State Normal Fluid channel E Quasiparticles (Normal Fluid) 2 D Energy Gap 0 sn Ls Cooper Pairs (Super Fluid) Superfluid channel Current-carrying superconductor J J = s E s = sn – i s 2 Js Jn sn = nne 2 t/m s 2 = nse 2/mw ns(T) n 0 11 J = Js + Jn nn(T) Tc T n = ns(T) + nn(T) nn = number of QPs ns = number of SC electrons t = QP momentum relaxation time m = carrier mass w = frequency

s = s 1 -is 2 (p nse 2/m)d(w) Superconductor Electrodynamics T = 0 s 1 (w ) s 2(w) ~ 1/w ideal s-wave Normal State (T > Tc) (Drude Model) s 2 (w ) ns(T) s 1( w ) Superfluid density l 2 ~ m/ns ~ 1/wps 2 0 0 w 1/t 0 0 Tc “binding energy” of Cooper pair (100 GHz ~ few THz) Surface Impedance (w > 0) Normal State Superconducting State (w < 2 D) Penetration depth l(0) ~ 20 – 200 nm Finite-temperature: Xs(T) = w. L = wm 0 l(T) → ∞ as T →Tc (and wps(T) → 0) Narrow wire or thin film of thickness t : L(T) = m 0 l(T) coth(t/l(T)) → m 0 l 2(T)/t Kinetic Inductance 12 T

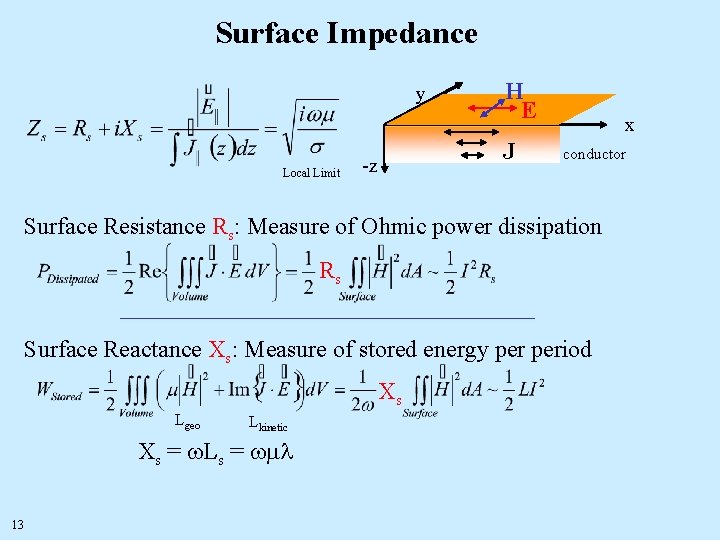
Surface Impedance y Local Limit H E J -z x conductor Surface Resistance Rs: Measure of Ohmic power dissipation Rs Surface Reactance Xs: Measure of stored energy period Xs Lgeo Lkinetic Xs = w. Ls = wml 13

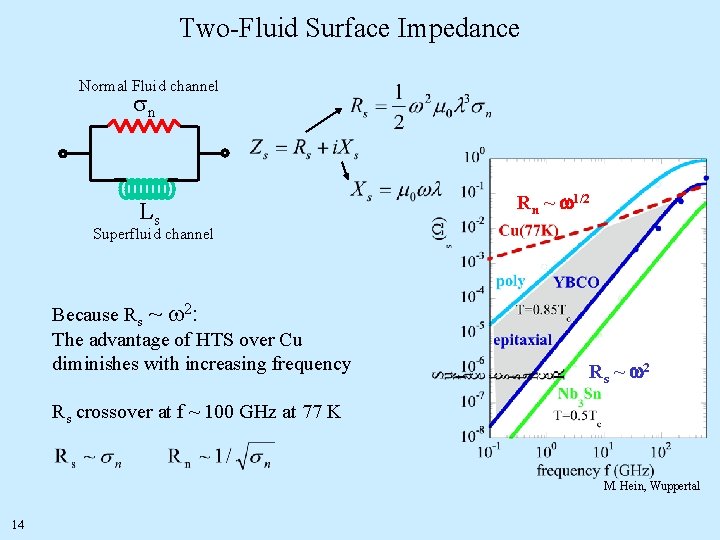
Two-Fluid Surface Impedance Normal Fluid channel sn Rn ~ 1/2 Ls Superfluid channel Because Rs ~ w 2: The advantage of HTS over Cu diminishes with increasing frequency R s ~ 2 Rs crossover at f ~ 100 GHz at 77 K M. Hein, Wuppertal 14

The London Equations t = momentum relaxation time Js = ns e vs Newton’s 2 nd Law for a charge carrier Superconductor: 1/t 0 1 st London Equation 1 st London Eq. and (Faraday) yield: London surmise 2 nd London Equation These equations yield the Meissner screening vacuum superconductor l. L is frequency independent (w < 2 D) 15 l. L ~ 20 – 200 nm

The London Equations continued Normal metal Superconductor E is the source of Jn E=0: Js goes on forever B is the source of Js, spontaneous flux exclusion Lenz’s Law 1 st London Equation E is required to maintain an ac current in a SC Cooper pair has finite inertia QPs are accelerated and dissipation occurs 16

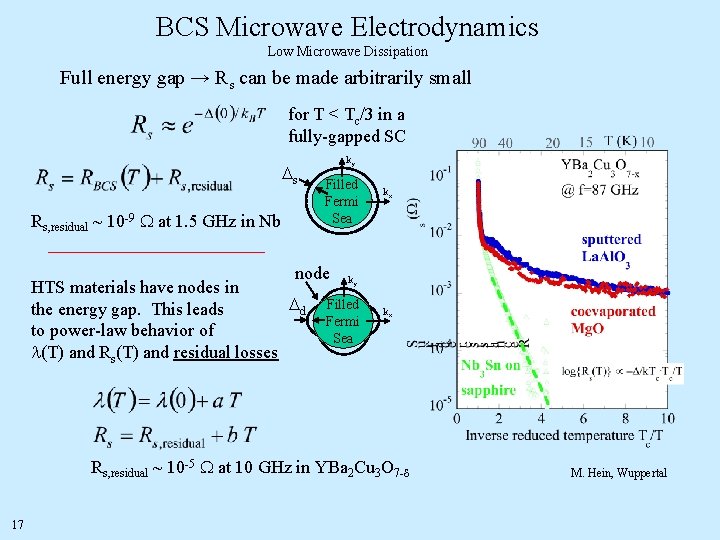
BCS Microwave Electrodynamics Low Microwave Dissipation Full energy gap → Rs can be made arbitrarily small for T < Tc/3 in a fully-gapped SC Ds Rs, residual ~ 10 -9 W at 1. 5 GHz in Nb ky Filled Fermi Sea node HTS materials have nodes in Dd the energy gap. This leads to power-law behavior of l(T) and Rs(T) and residual losses kx ky Filled Fermi Sea kx Rs, residual ~ 10 -5 W at 10 GHz in YBa 2 Cu 3 O 7 -d 17 M. Hein, Wuppertal

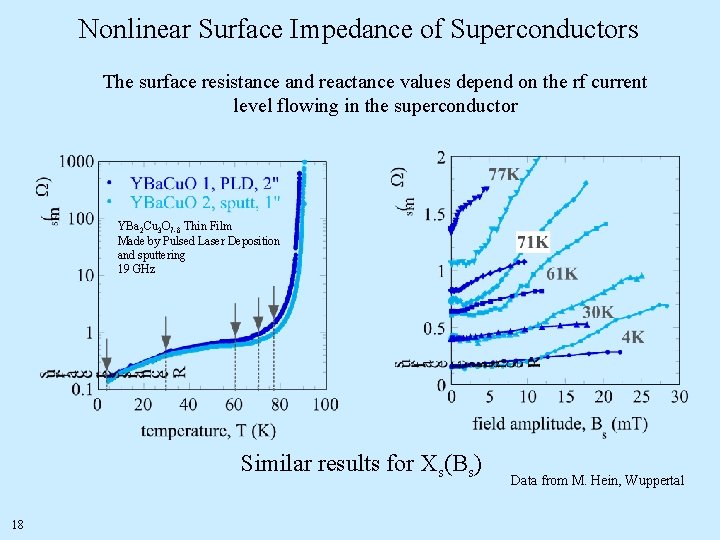
Nonlinear Surface Impedance of Superconductors The surface resistance and reactance values depend on the rf current level flowing in the superconductor YBa 2 Cu 3 O 7 -d Thin Film Made by Pulsed Laser Deposition and sputtering 19 GHz Similar results for Xs(Bs) 18 Data from M. Hein, Wuppertal

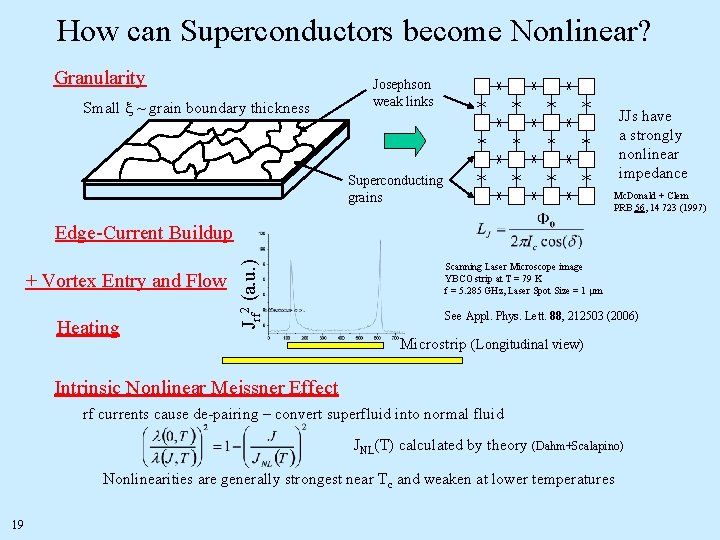
How can Superconductors become Nonlinear? Granularity Josephson weak links Small x ~ grain boundary thickness JJs have a strongly nonlinear impedance Superconducting grains Mc. Donald + Clem PRB 56, 14 723 (1997) + Vortex Entry and Flow Heating Jrf 2 (a. u. ) Edge-Current Buildup Scanning Laser Microscope image YBCO strip at T = 79 K f = 5. 285 GHz, Laser Spot Size = 1 mm See Appl. Phys. Lett. 88, 212503 (2006) Microstrip (Longitudinal view) Intrinsic Nonlinear Meissner Effect rf currents cause de-pairing – convert superfluid into normal fluid JNL(T) calculated by theory (Dahm+Scalapino) Nonlinearities are generally strongest near Tc and weaken at lower temperatures 19

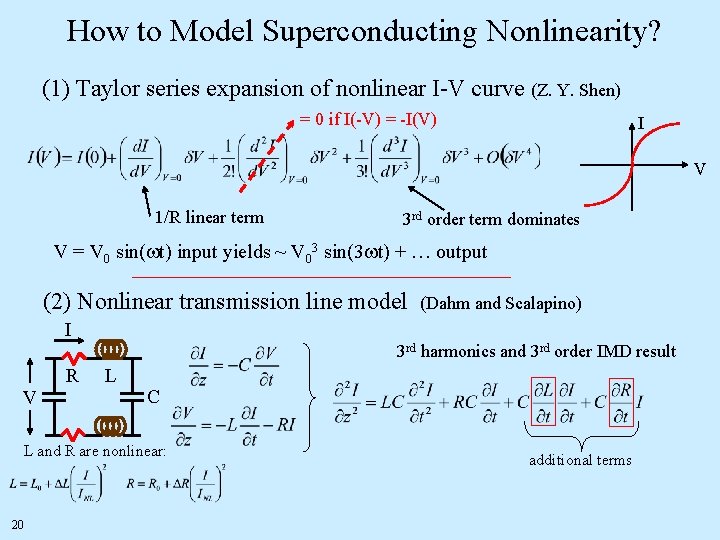
How to Model Superconducting Nonlinearity? (1) Taylor series expansion of nonlinear I-V curve (Z. Y. Shen) = 0 if I(-V) = -I(V) I V 1/R linear term 3 rd order term dominates V = V 0 sin(wt) input yields ~ V 03 sin(3 wt) + … output (2) Nonlinear transmission line model (Dahm and Scalapino) I 3 rd harmonics and 3 rd order IMD result R V L C L and R are nonlinear: additional terms 20

Experimental High Frequency Superconductivity • Resonators • Cavity Perturbation • Measurements of Nonlinearity • Topics of Current Interest • Microwave Microscopy 21

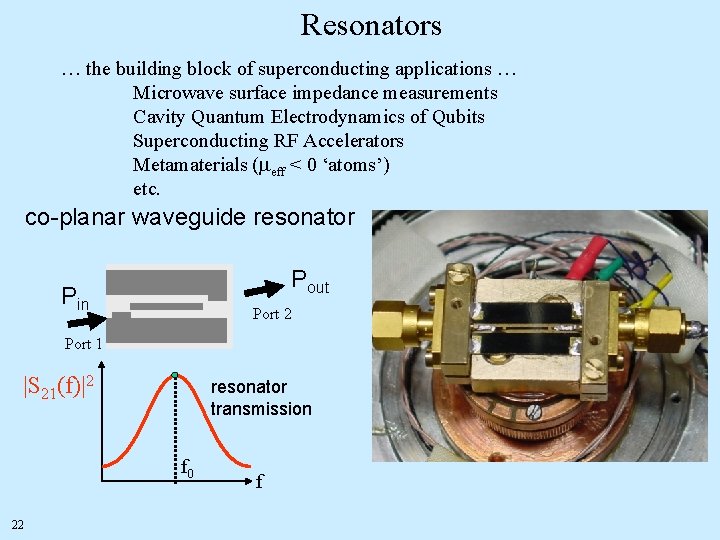
Resonators … the building block of superconducting applications … Microwave surface impedance measurements Cavity Quantum Electrodynamics of Qubits Superconducting RF Accelerators Metamaterials (meff < 0 ‘atoms’) etc. co-planar waveguide resonator Pout Pin Port 2 Port 1 |S 21(f)|2 resonator transmission f 0 f 22

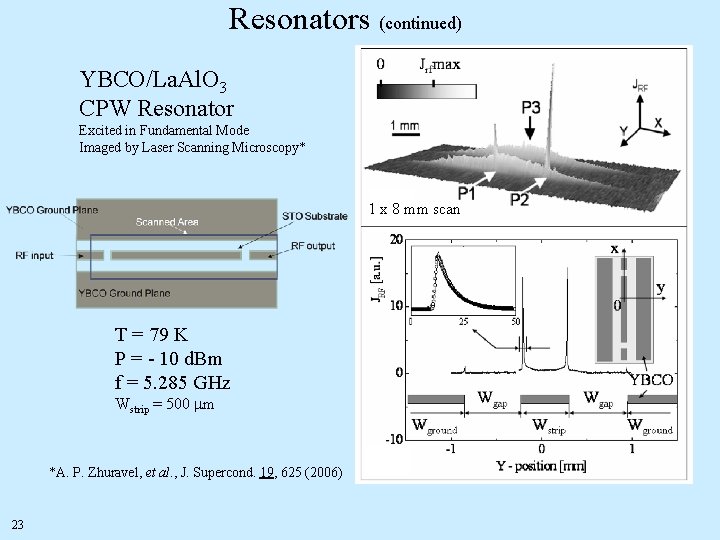
Resonators (continued) YBCO/La. Al. O 3 CPW Resonator Excited in Fundamental Mode Imaged by Laser Scanning Microscopy* 1 x 8 mm scan T = 79 K P = - 10 d. Bm f = 5. 285 GHz Wstrip = 500 mm *A. P. Zhuravel, et al. , J. Supercond. 19, 625 (2006) 23

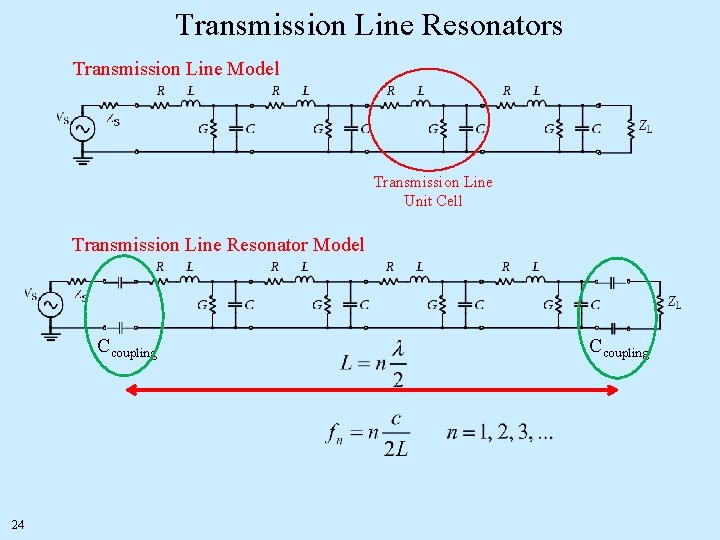
Transmission Line Resonators Transmission Line Model Transmission Line Unit Cell Transmission Line Resonator Model Ccoupling 24

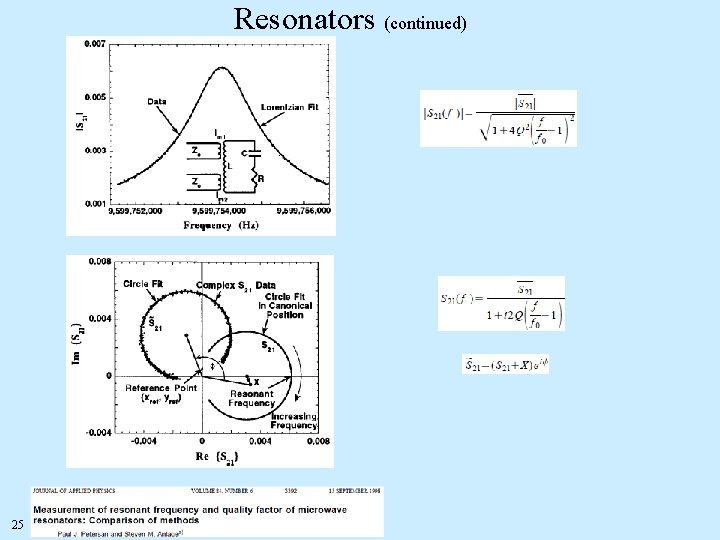
Resonators (continued) 25

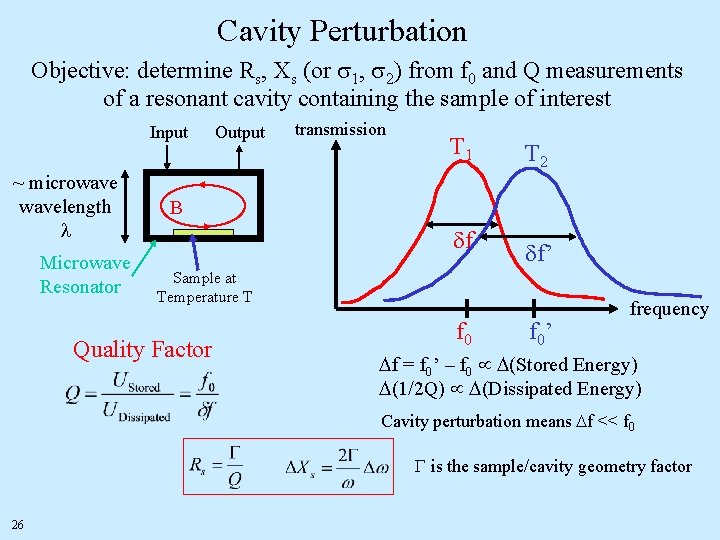
Cavity Perturbation Objective: determine Rs, Xs (or s 1, s 2) from f 0 and Q measurements of a resonant cavity containing the sample of interest Input ~ microwavelength l Microwave Resonator Output transmission T 1 T 2 B df df’ Sample at Temperature T f 0 Quality Factor f 0’ frequency Df = f 0’ – f 0 D(Stored Energy) D(1/2 Q) D(Dissipated Energy) Cavity perturbation means Df << f 0 G is the sample/cavity geometry factor 26

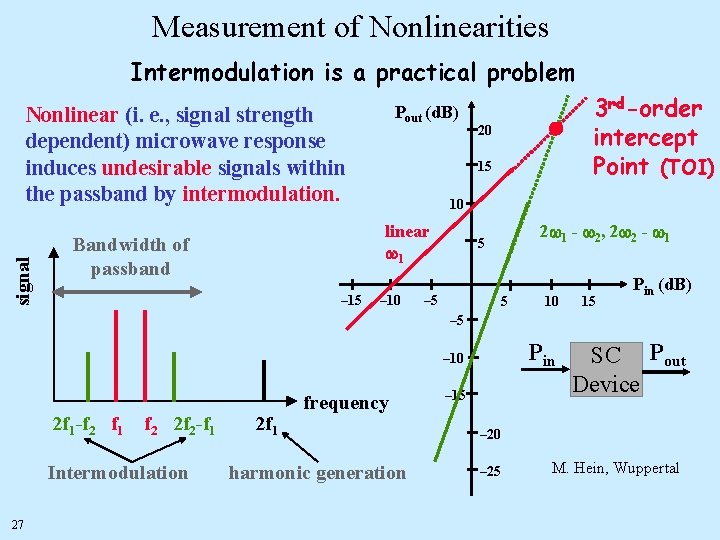
Measurement of Nonlinearities Intermodulation is a practical problem Pout (d. B) signal Nonlinear (i. e. , signal strength dependent) microwave response induces undesirable signals within the passband by intermodulation. 3 rd-order intercept Point (TOI) 20 15 10 linear 1 Bandwidth of passband – 15 – 10 2 1 - 2, 2 2 - 1 5 – 5 5 10 15 Pin (d. B) – 5 Pin – 10 2 f 1 -f 2 f 1 f 2 2 f 2 -f 1 Intermodulation 2 f 1 frequency – 20 harmonic generation 27 – 15 SC Pout Device – 25 M. Hein, Wuppertal

Topics of Current Interest In Microwave Superconductivity Research Identifying and eliminating the microscopic sources of extrinsic nonlinearity Increase device yield Allows further miniaturization of devices Allow development of ILC Nb cavities with BCS-limited properties Superconducting Metamaterials: J. Opt. 13, 024001 (2011) Low-loss, compact, tunable metamaterial ‘atoms’ Controlling de-coherence in superconducting qubits Identify and eliminate two-level systems in dielectrics 28

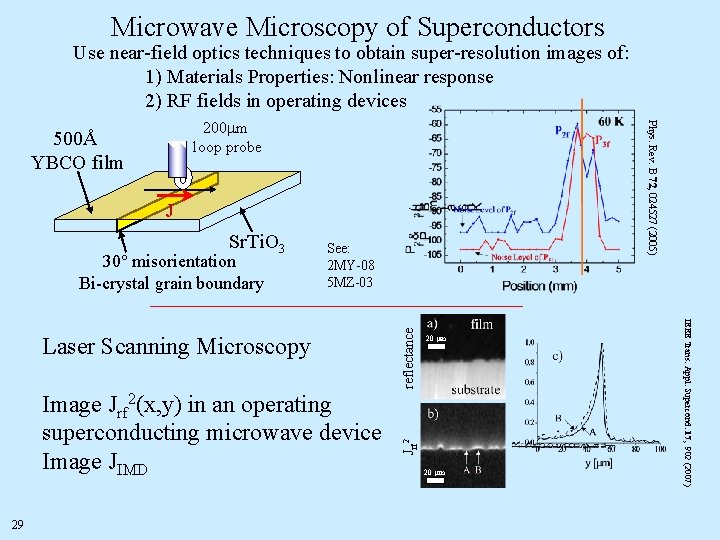
Microwave Microscopy of Superconductors Use near-field optics techniques to obtain super-resolution images of: 1) Materials Properties: Nonlinear response 2) RF fields in operating devices Phys. Rev. B 72, 024527 (2005) 200 mm loop probe 500Å YBCO film J See: 2 MY-08 5 MZ-03 Laser Scanning Microscopy Image Jrf 2(x, y) in an operating superconducting microwave device Image JIMD 29 20 mm IEEE Trans. Appl. Supercond. 17, 902 (2007) reflectance 30° misorientation Bi-crystal grain boundary Jrf 2 Sr. Ti. O 3

Superconducting Metamaterials Build artificial ‘atoms’ with tailored electric and magnetic response An array of these sub-wavelength ‘atoms’ are described by eeff, meff 30

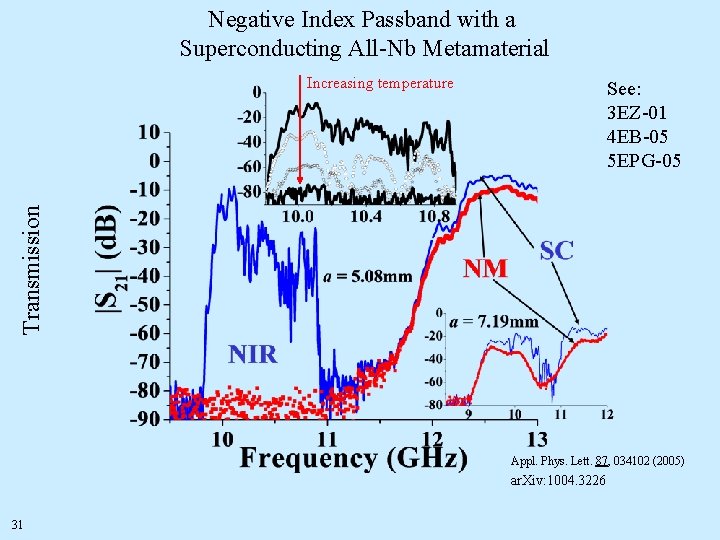
Negative Index Passband with a Superconducting All-Nb Metamaterial Increasing temperature Transmission See: 3 EZ-01 4 EB-05 5 EPG-05 Appl. Phys. Lett. 87, 034102 (2005) ar. Xiv: 1004. 3226 31

References and Further Reading Z. Y. Shen, “High-Temperature Superconducting Microwave Circuits, ” Artech House, Boston, 1994. M. J. Lancaster, “Passive Microwave Device Applications, ” Cambridge University Press, Cambridge, 1997. M. A. Hein, “HTS Thin Films at Microwave Frequencies, ” Springer Tracts of Modern Physics 155, Springer, Berlin, 1999. “Microwave Superconductivity, ” NATO- ASI series, ed. by H. Weinstock and M. Nisenoff, Kluwer, 2001. T. Van. Duzer and C. W. Turner, “Principles of Superconductive Devices and Circuits, ” Elsevier, 1981. T. P. Orlando and K. A. Delin, “Fundamentals of Applied Superconductivity, ” Addison-Wesley, 1991. R. E. Matick, “Transmission Lines for Digital and Communication Networks, ” IEEE Press, 1995; Chapter 6. Alan M. Portis, “Electrodynamcis of High-Temperature Superconductors, ” World Scientific, Singapore, 1993. 32

Superconductivity Links Wikipedia article on Superconductivity http: //en. wikipedia. org/wiki/Superconductivity Superconductor Information for the Beginner http: //www. superconductors. org/ Gallery of Abrikosov Vortex Lattices http: //www. fys. uio. no/super/vortex/ Graduate course on Superconductivity (Anlage) http: //www. physics. umd. edu/courses/Phys 798 S/anlage/Phys 798 SAnlage. Spring 06/index. html You. Tube videos of Superconductivity (Alfred Leitner) http: //www. youtube. com/watch? v=n. LWUt. UZv. OP 8 33

Please Ask Questions! 34