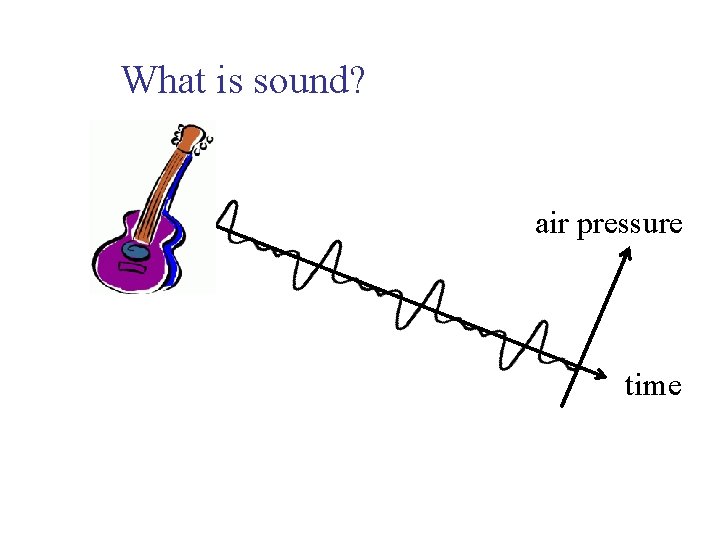
Fundamentals of Musical Acoustics What is sound air


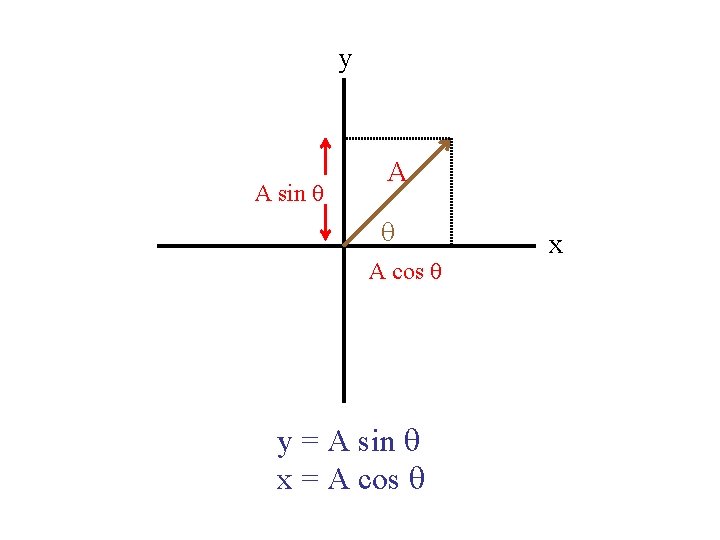



- Slides: 37

Fundamentals of Musical Acoustics

What is sound? air pressure time

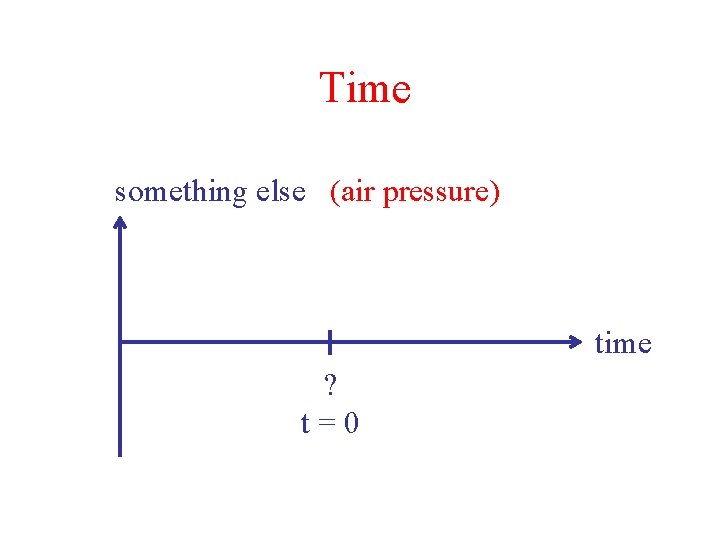
Time something else (air pressure) time ? t=0

These variations in air pressure over time can be decomposed into sine waves with amplitude and frequency

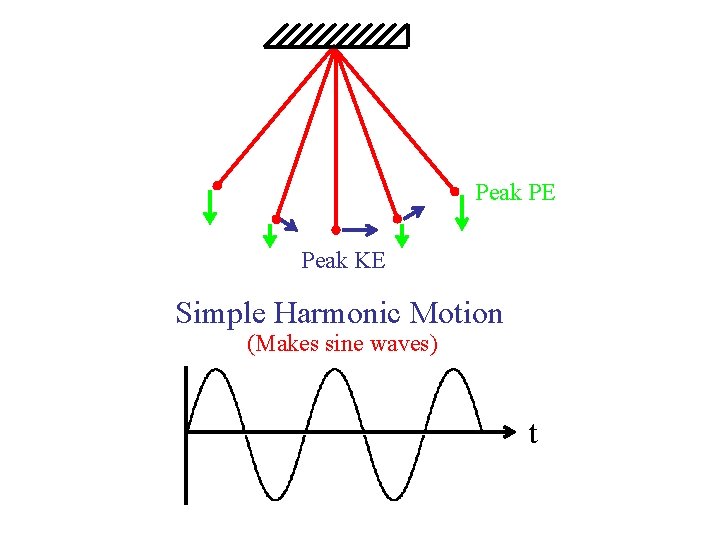
Peak PE Peak KE Simple Harmonic Motion (Makes sine waves) t

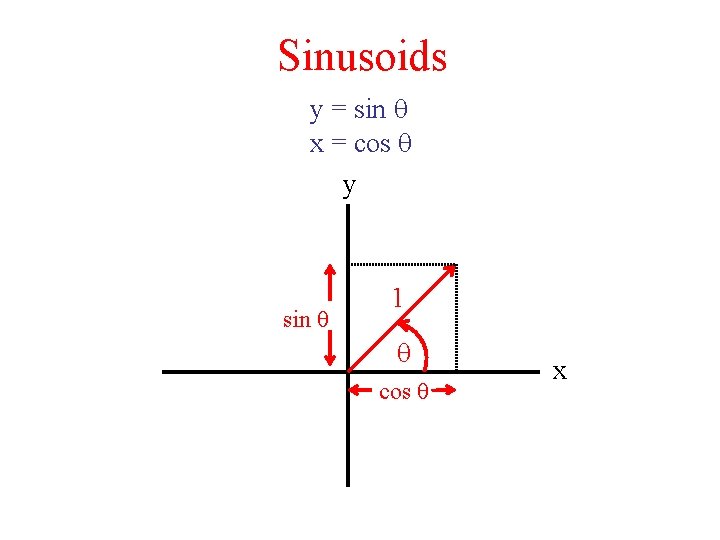
Sinusoids y = sin q x = cos q y sin q 1 q cos q x

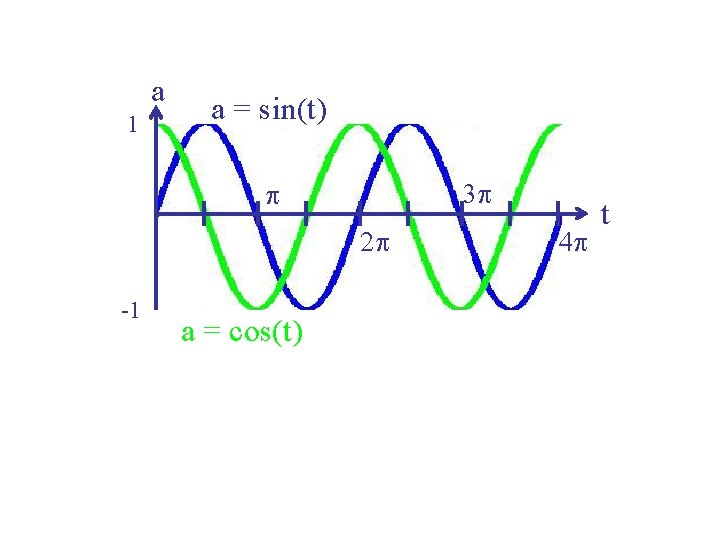
a 1 a = sin(t) 3 p p 2 p -1 a = cos(t) 4 p t

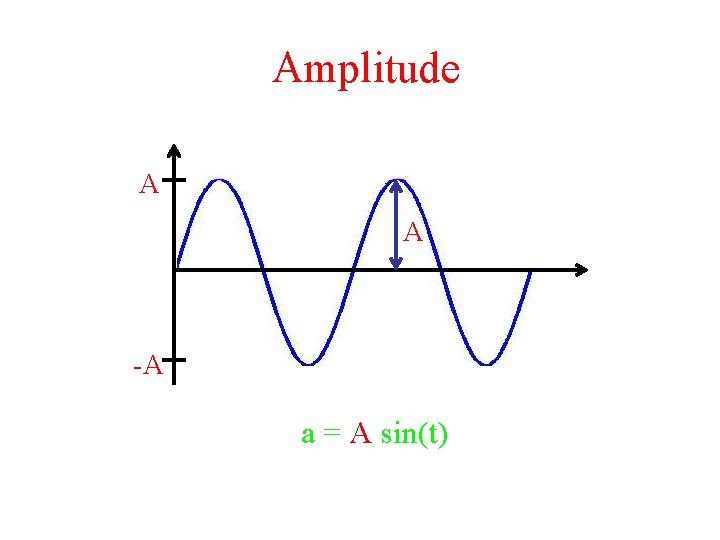
Amplitude A A -A a = A sin(t)
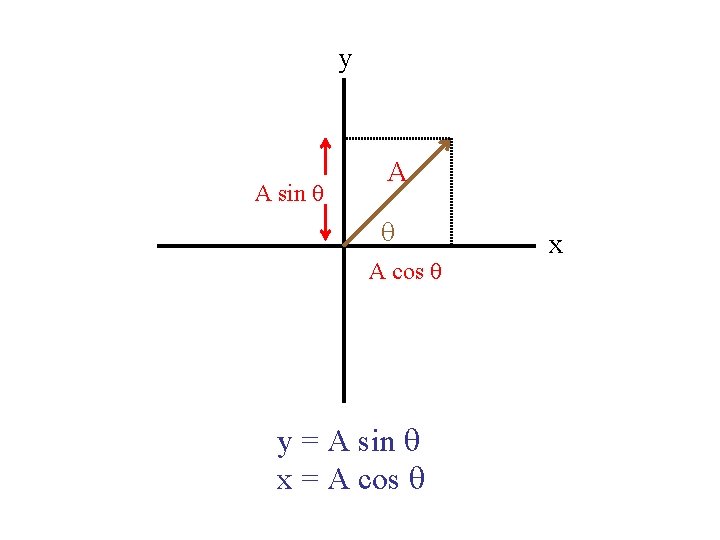
y A sin q A cos q y = A sin q x = A cos q x

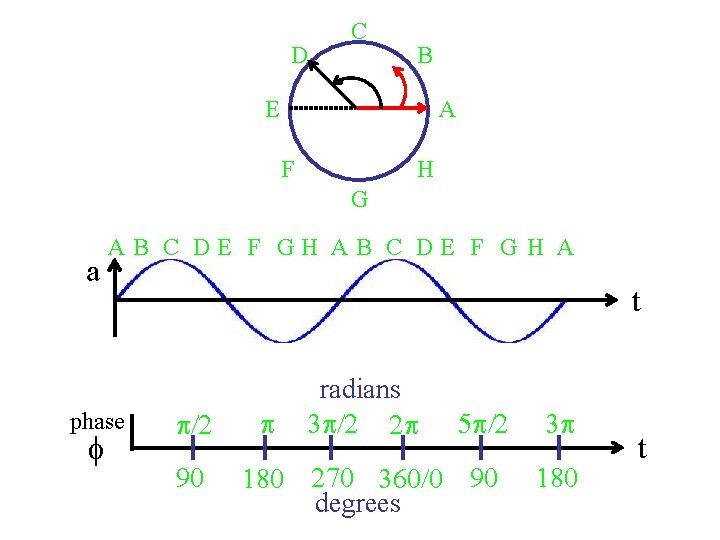
Frequency How frequently does the sin/cos complete a whole cycle?

D C B E A F H G a AB C DE F GH AB C DE F G H A phase f t p/2 90 p radians 3 p/2 2 p 5 p/2 180 270 360/0 90 degrees 3 p 180 t

Frequency 1 cycle / sec. 2 p 2 p / sec. . f cycles / sec. f 2 p / sec.

Radian Frequency w = 2 pf f = w/2 p

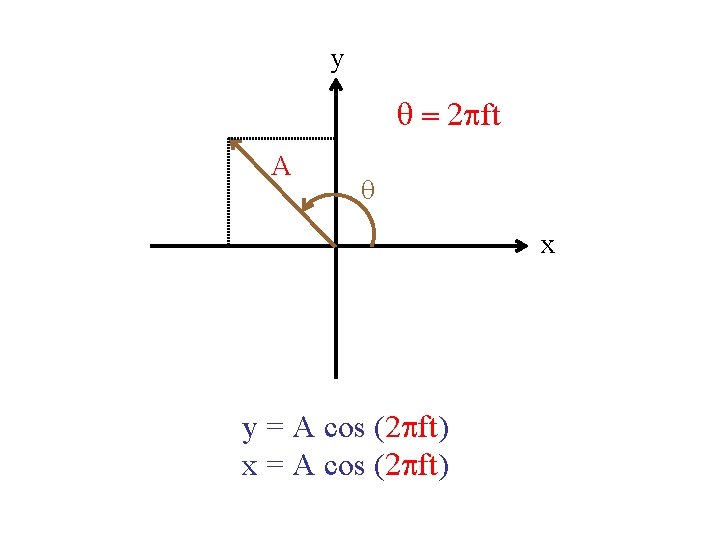
y q = 2 pft A q x y = A cos (2 pft) x = A cos (2 pft)

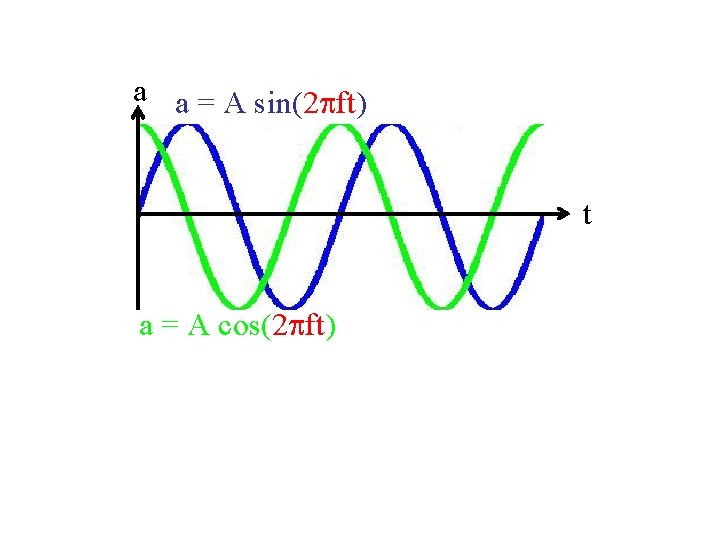
a a = A sin(2 pft) t a = A cos(2 pft)

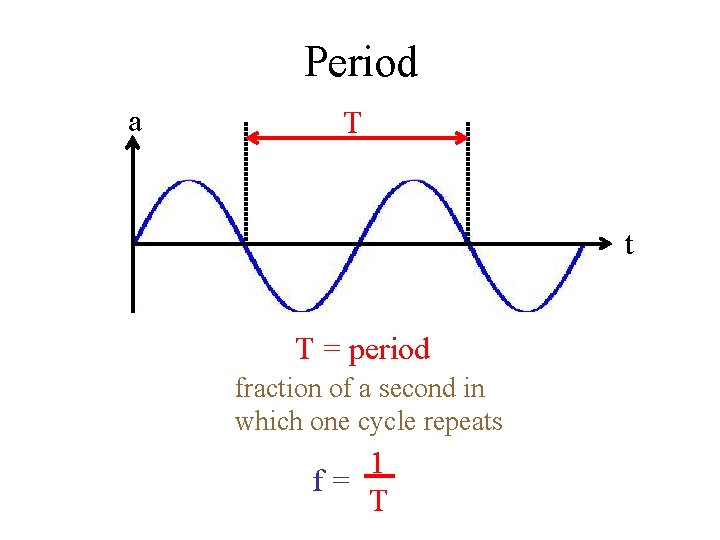
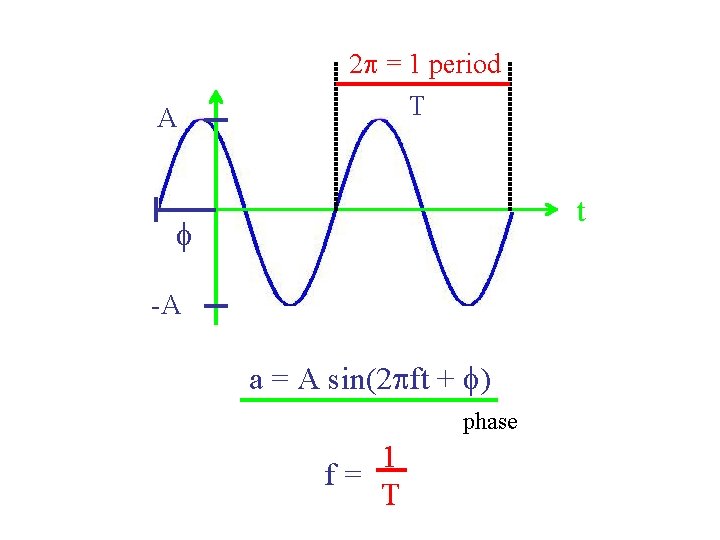
Period a T t T = period fraction of a second in which one cycle repeats 1 f= T

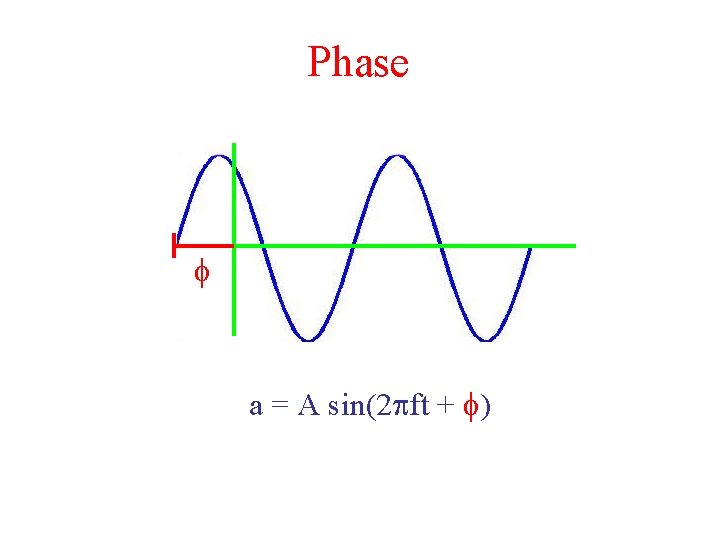
Phase f a = A sin(2 pft + f)

A 2 p = 1 period T t f -A a = A sin(2 pft + f) phase 1 f= T

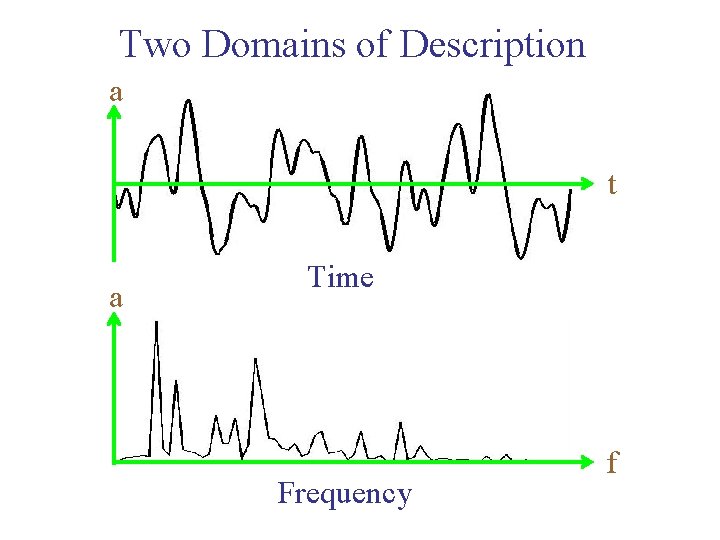
Two Domains of Description a t a Time Frequency f

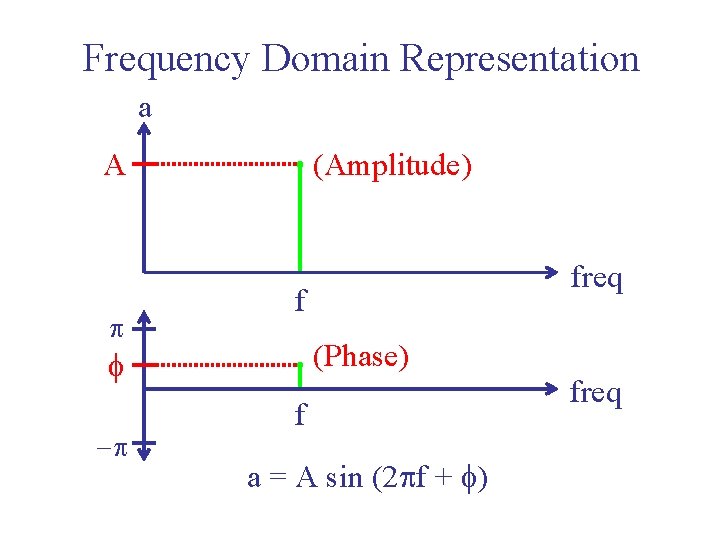
Frequency Domain Representation a A p (Amplitude) f (Phase) f -p freq f a = A sin (2 pf + f) freq

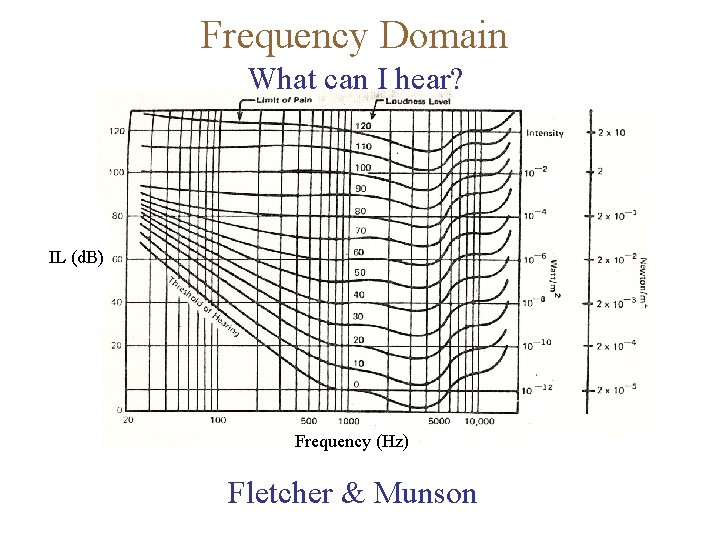
Frequency Domain What can I hear? IL (d. B) Frequency (Hz) Fletcher & Munson

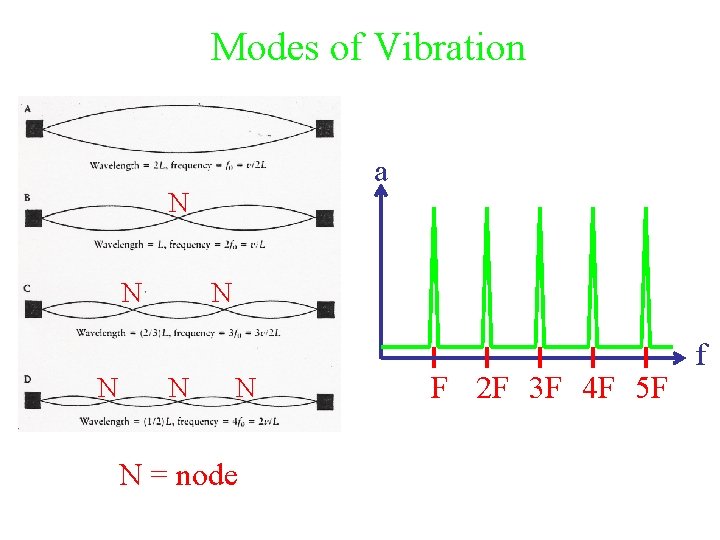
Modes of Vibration a N N N N = node F 2 F 3 F 4 F 5 F f

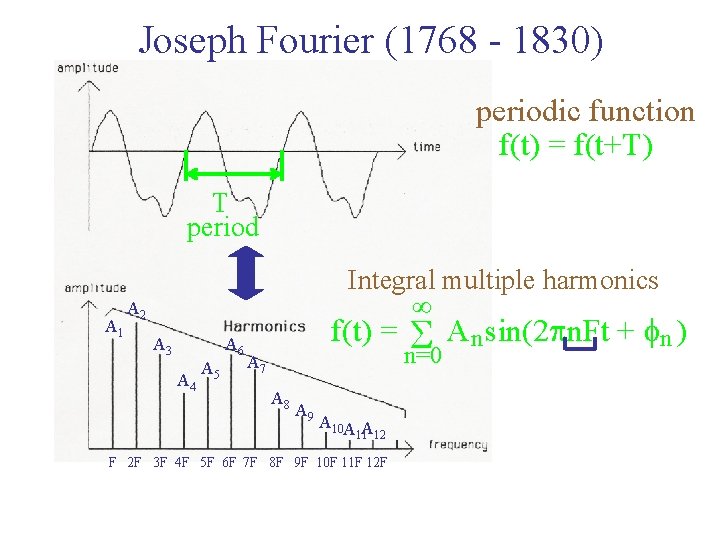
Joseph Fourier (1768 - 1830) periodic function f(t) = f(t+T) T period A 1 Integral multiple harmonics ∞ A 2 A 3 A 6 A 4 A 5 f(t) = A 7 A 8 A 9 A 10 A A 11 12 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F A n sin(2 pn. Ft + fn ) S n=0

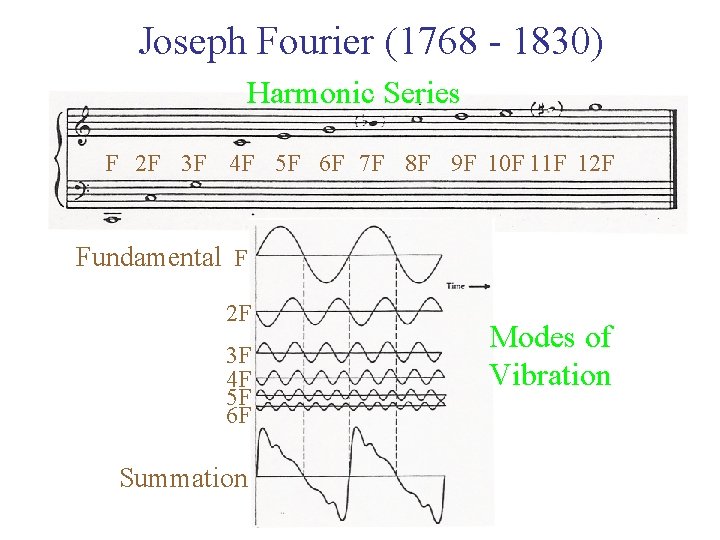
Joseph Fourier (1768 - 1830) Harmonic Series F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F Fundamental F 2 F 3 F 4 F 5 F 6 F Summation Modes of Vibration

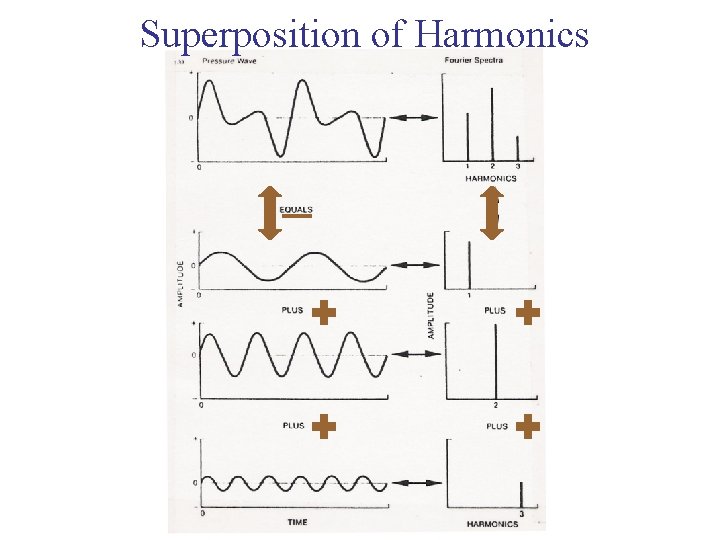
Superposition of Harmonics

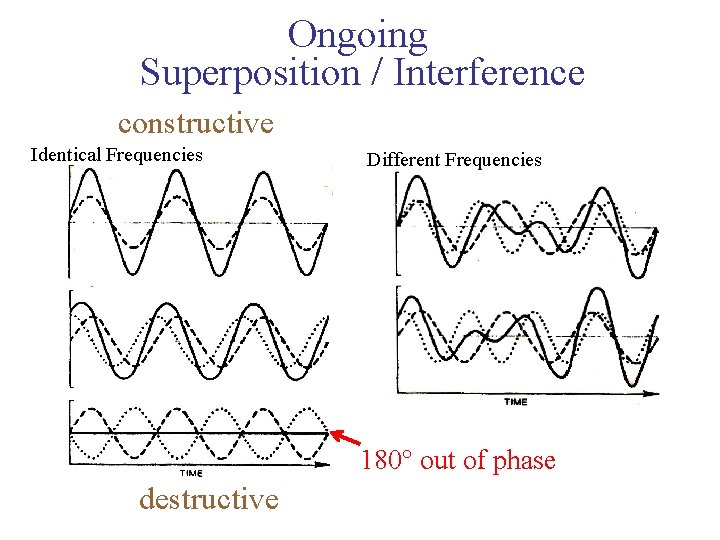
Ongoing Superposition / Interference constructive Identical Frequencies Different Frequencies 180° out of phase destructive

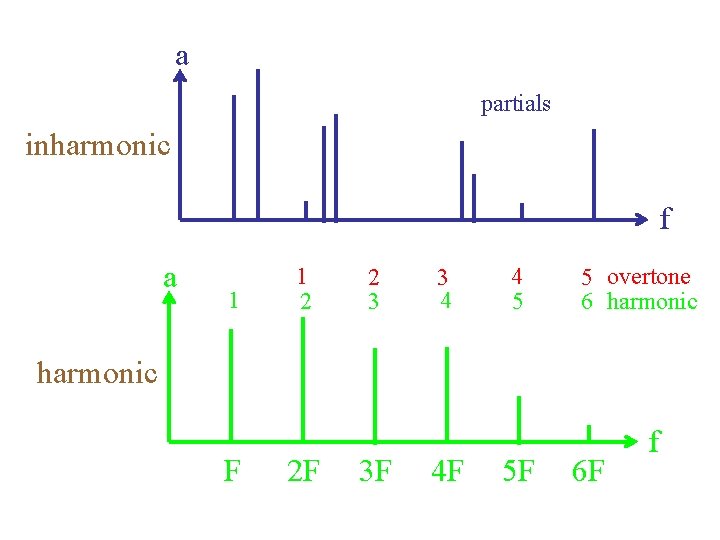
a partials inharmonic f a 1 1 2 2 3 3 4 4 5 5 overtone 6 harmonic F 2 F 3 F 4 F 5 F 6 F f

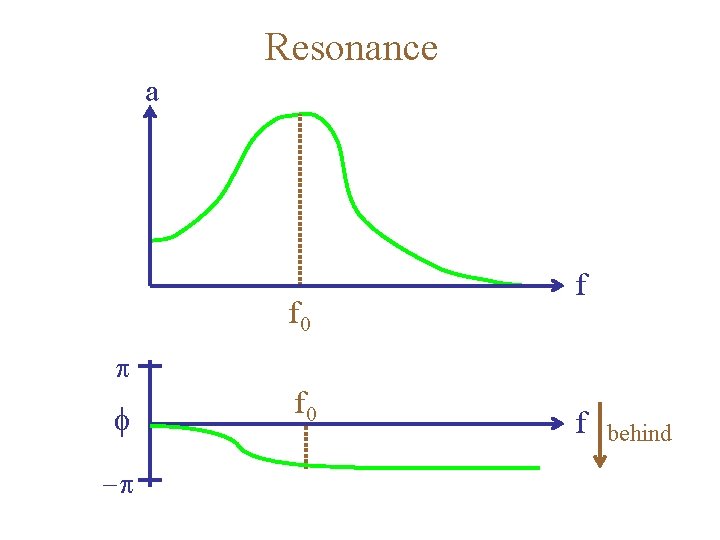
Resonance a f 0 f p f -p f 0 f behind

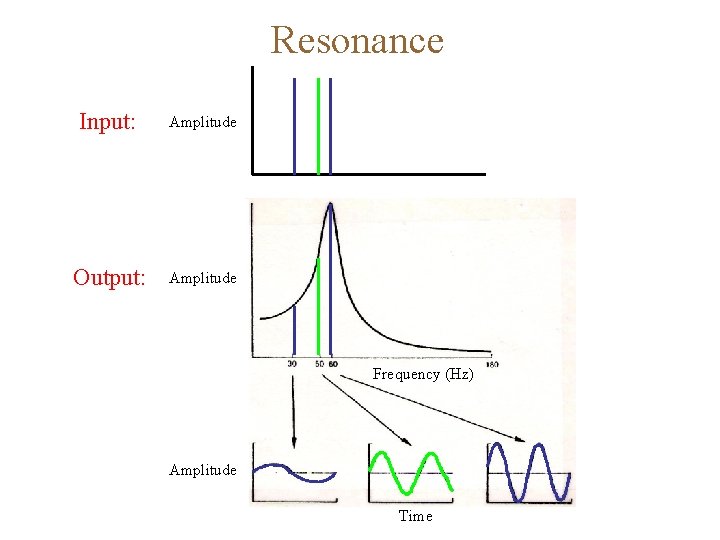
Resonance Input: Amplitude Output: Amplitude Frequency (Hz) Amplitude Time

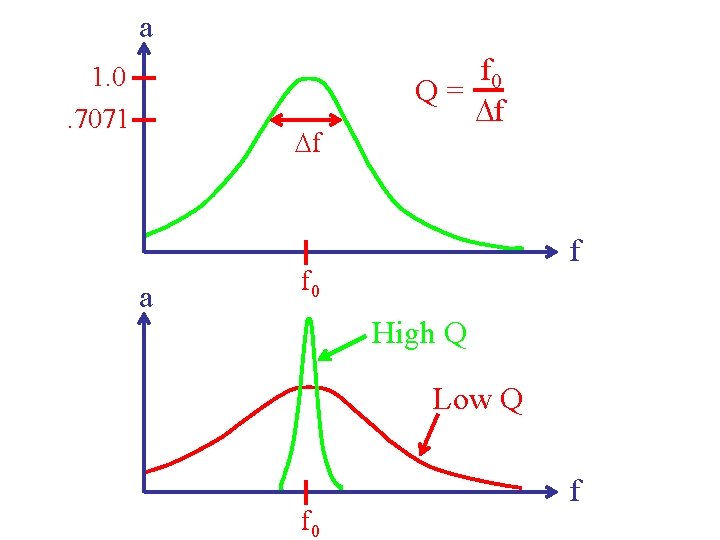
a 1. 0. 7071 Df a f 0 Q= Df f f 0 High Q Low Q f 0 f

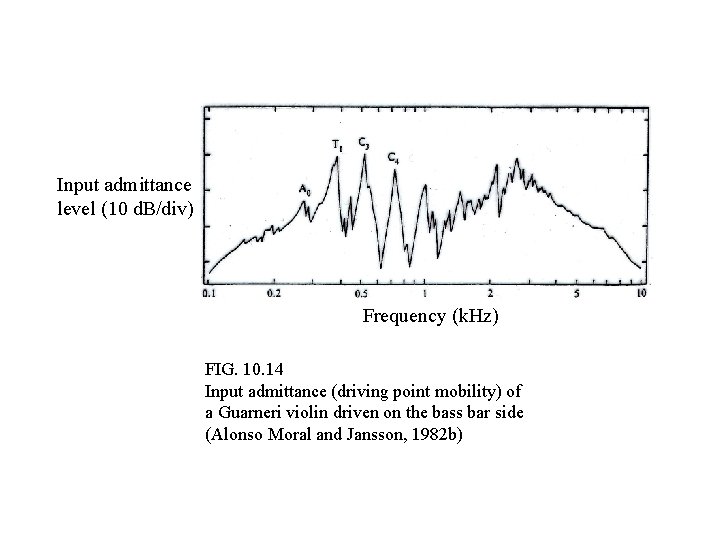
Input admittance level (10 d. B/div) Frequency (k. Hz) FIG. 10. 14 Input admittance (driving point mobility) of a Guarneri violin driven on the bass bar side (Alonso Moral and Jansson, 1982 b)

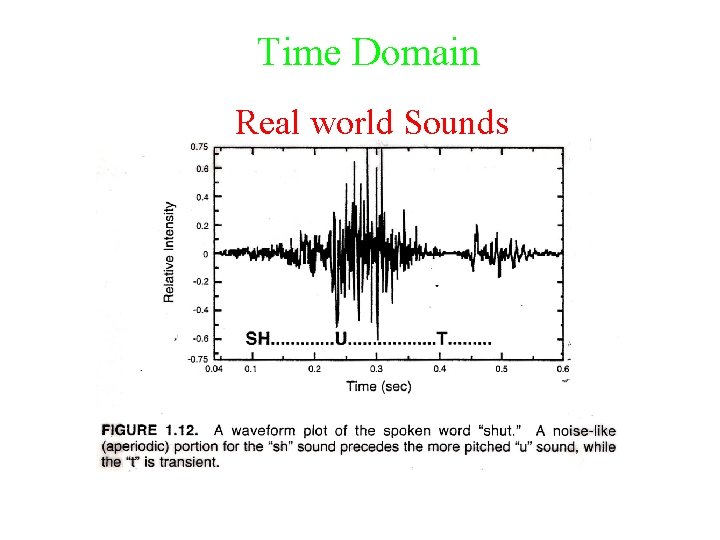
Time Domain Real world Sounds

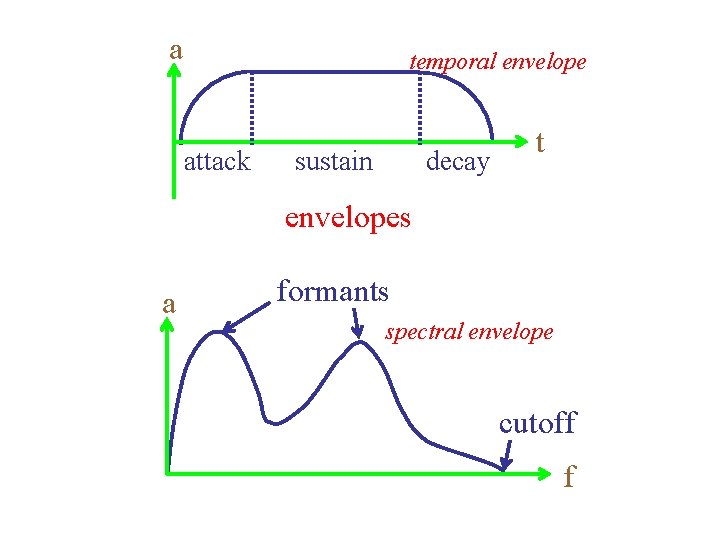
a temporal envelope attack sustain decay t envelopes a formants spectral envelope cutoff f

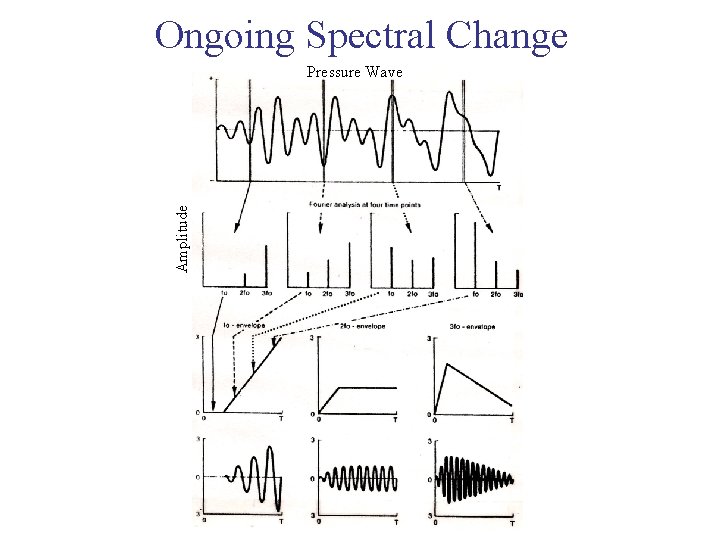
Ongoing Spectral Change Amplitude Pressure Wave

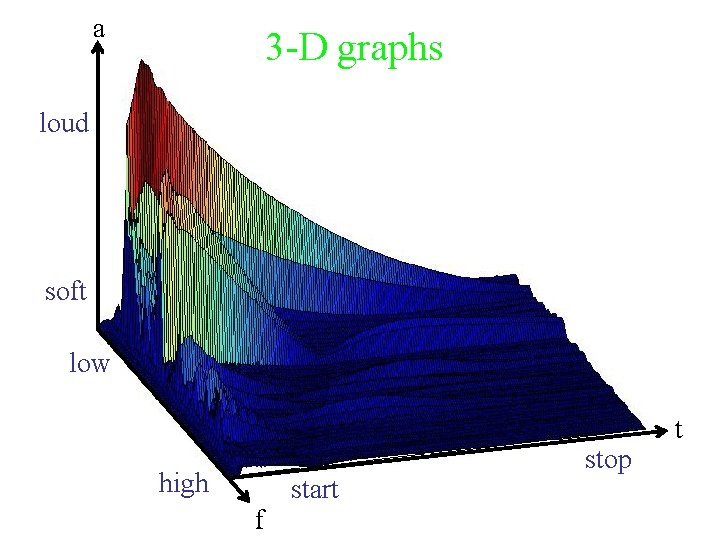
a 3 -D graphs loud soft low high start f stop t


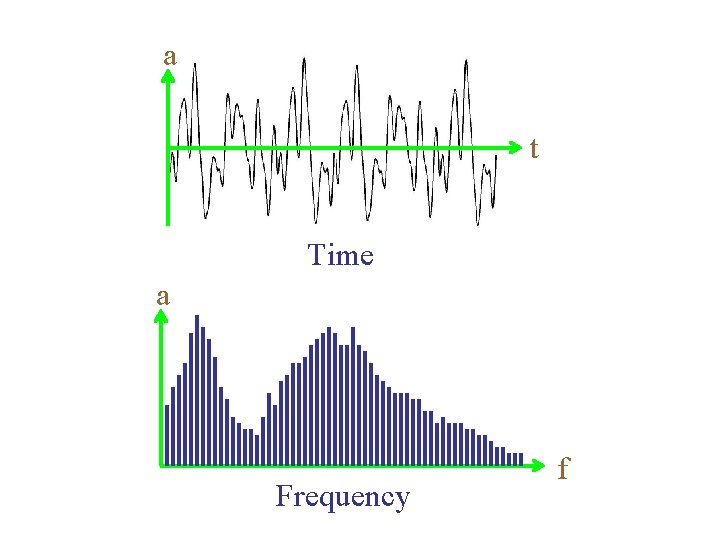
a t Time a Frequency f