Fundamentals of Functional Programming Computer Science Functional Programming

Fundamentals of Functional Programming Computer Science

Functional Programming • We need to get our programming language set up before we look at functional programming We’ll be using Haskell Download from here: https: //www. haskell. org/platform Choose Full option • Once set up, need to run GHCi to run Haskell scripts First go to folder, : cd “file_path” Then load script, : load “file_name. hs”

Functional Programming • Functional Programming is a paradigm A ‘way of thinking’, or ‘strict thought process’ • Involves thinking of program execution in terms of running individual functions Functions are more mathematical in nature than Object-Orientated Programming • Functional Programming has three properties: Immutable functions Stateless operation Higher-Order functions (once a function has been made, it can’t be changed) (functions do not make use of outside values) (functions are used as parameters)

Functional Programming • Functions can be thought of as two things: A process – transforms information from one form into another An object – something that can act on other functions/pieces of data • Take, for example, a sharpener As a process – sharpen the pencil As an object – the sharpener’s size, weight, colour

• The input set is the domain The output set is the codomain

Function Types • Here are some of the types we can use in Haskell Integer Char Float String Double Bool

Function Types • Here is an example of a Haskell function that triples a single number • We have to save it to a Haskell script file (. hs) and load it in GHCi before we can use it

Function Types • With functions, the last type is the return type The other types are inputs • So we can create a function with multiple inputs really easily

• Try creating Haskell functions for the following: Finding the square of a number Finding the cube of a number Function to double a number Finding the difference between two numbers Finding the area of a triangle

Functions as Parameters • Functions are considered first class objects Can be used as parameters Can be returned by functions • This function doubles the result of another function

Functions as Parameters • Note that brackets in function signatures are not needed They help us understand what the function should be doing • Typically brackets represent a single value In the type, they represent a single function • They are needed in calculations when a single value is expected

Functions as Return Values • As mentioned earlier, functions can also be returned • This function takes an integer, and returns an exponentiation function based off that integer

Functions as Return Values • That bit at the end is an anonymous function Before the arrow are the parameters After the arrow is the return value • So we’re creating a function in a function And returning it

Partial Function Application • We can also give a function most of its parameters This won’t break We just need to store the result in another function • When partially applying a function, we’re actually making another function With some of the values set • We can finish the function by adding the remaining parameters

Partial Function Application • Here’s an example of it in action • We can use let in GHCi to temporarily make a function • The double function is made from partially applying mult

Function Composition •

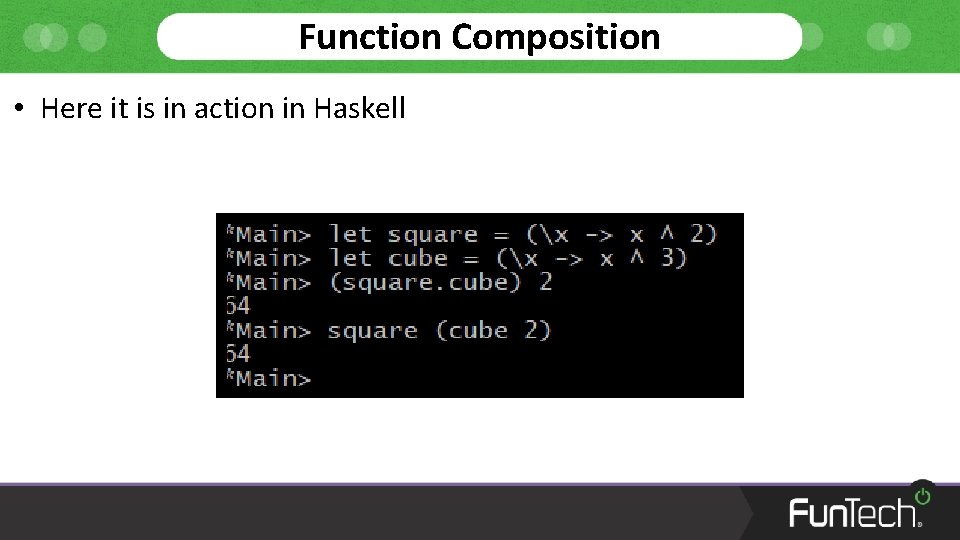
Function Composition • Here it is in action in Haskell

Interesting GHCi Prelude Functions • The Prelude is Haskell’s base function library Where types like Integer, and functions like square-root come from • Here’s a list of some of them Give them a try yourself sqrt 3 div 5 2 mod 5 2 cos 0 sin (0. 5 * pi) gcd 45 54 lcm 4 5 take 5 “Hello World” drop 6 “Hello World” split. At 6 “Hello World” words “The black cat sat on the mat!” (^) 2 4

Haskell Types: Characters • Characters are represented usingle quotes Example: ‘a’ • We can also use the actual ASCII code for the base ASCII table Between 0 and 127 Example: ‘97’ • Can make individual characters upper/lower case Using to. Upper and to. Lower Can also check using is. Upper and is. Lower

Haskell Types: Numbers • There are lots of different number types (under the Number umbrella) in Haskell Int: a whole number with 30 bits of precision Integer: a whole number with any number of bits of precision Float: single-precision floating point number Double: double-precision floating point number Rational: fractional type with no rounding error

Haskell Types: Numbers • The Number library offers quite a few functions we can use Mostly to do with rounding truncate 45. 34 round 45. 6 ceiling 5. 3 floor 5. 3 max 5 8 min 6 4

Haskell Types: Strings • Strings are literally a list of Char values Referred to as [Char] • String values need to be enclosed in double-quotes • Can concatenate Strings using the ++ operator “Functional” ++ “Programming” ++ actually appends lists (can be used with other data types)

Haskell Types: Bool • Represents true and false values • Bool values use a capital first letter True and False • Haskell supports the usual operators (logical and relational) AND (&&) OR (||) NOT (not) < > <= >= ==

Anonymous Functions • We saw this earlier when making a function that makes other functions (x -> x ^ 2) • Called anonymous functions Aren’t given a name • Are usually Assigned to another function Run in GHCi

Conditional Statements • Everything we’ve looked at so far as been sequential Running instructions one after the other • However, Haskell does have another construct we can use Branching • Can use it during the value we’re trying to return

Conditional Statements • Here is an example of a function that checks if a number is even

• Create the following functions is. Odd is. Positive

Pattern Recognition • There’s one really important thing to talk about in Haskell There is no iteration That means no while-loops or for-loops • Instead, functions have to make use of recursion to do anything • To do this, we need to include termination conditions Could be done using if/else statements Easier done using pattern recognition

Pattern Recognition • With this, we can state multiple possible values for a function to return From top-to-bottom • The function will only return one of them Like a switch-statement • If we want to return something first before other possibilities, we need to place it higher up in the function’s implementation

Pattern Recognition • Here is an example Acts as a recursive function For summing a number (and all numbers below it)

• Create the following functions factorial fibonnaci

Using Lists • There are no arrays in Haskell Only lists • Lists have quite a few functions we can run on them head: returns the first element tail: returns all elements after the first init: returns all elements before the last: returns the last element

Using Lists • Here’s an example of summing all the numbers in a list sum. List : : [Integer] -> Integer sum. List nums = if (null nums) then 0 else (head nums) + (sum. List (tail nums))

• Create the following functions product. List find. In. List

Using Map • We can also use lists in functions • Best example is the map function Applies a function to values in a list Returns a list with the return value stored in each position square. Nums : : [Integer] -> [Integer] square. Nums nums = map (x -> x ^ 2) nums

• Create the following functions double. Nums are. Nums. Even