Fundamentals of Electromagnetics for Teaching and Learning A













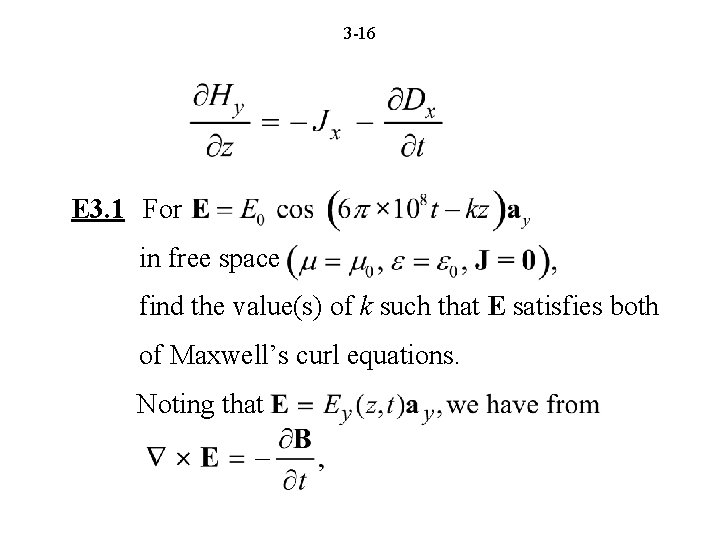
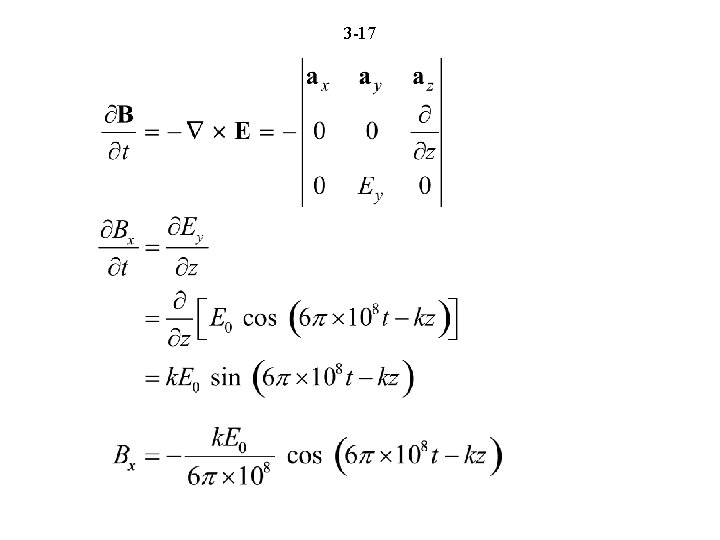


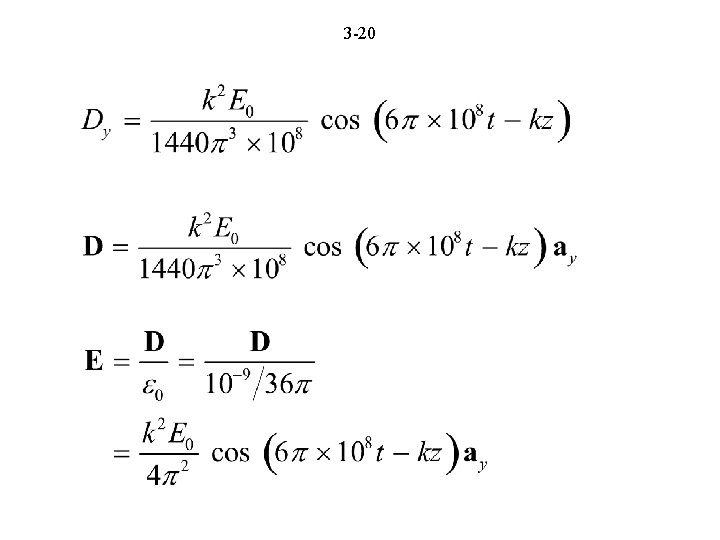










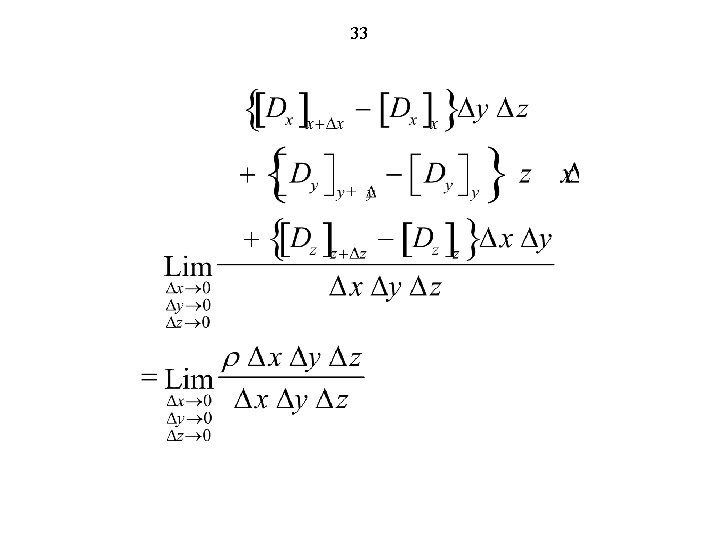


















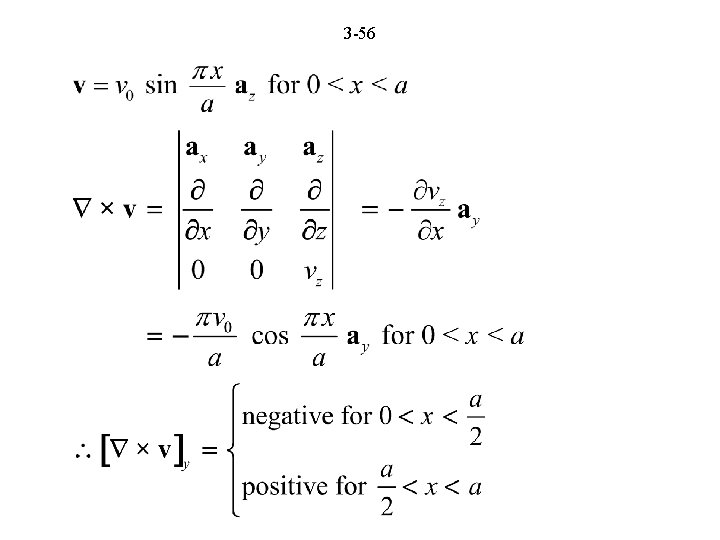


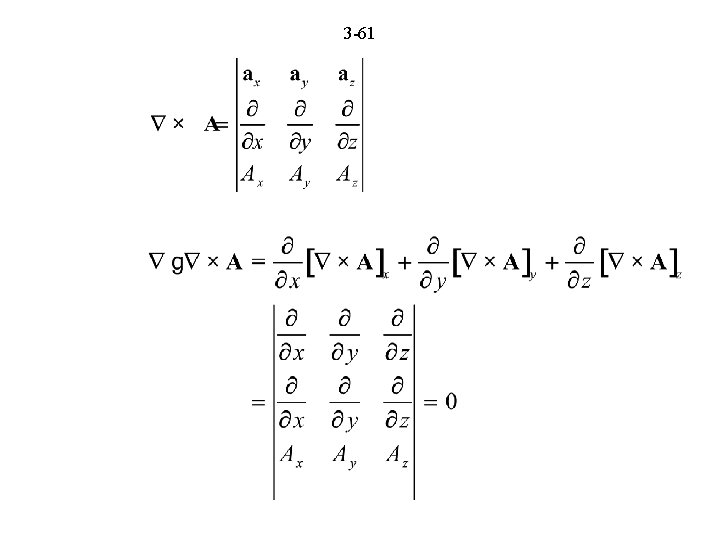







- Slides: 69

Fundamentals of Electromagnetics for Teaching and Learning: A Two-Week Intensive Course for Faculty in Electrical-, Electronics-, Communication-, and Computer- Related Engineering Departments in Engineering Colleges in India by Nannapaneni Narayana Rao Edward C. Jordan Professor Emeritus of Electrical and Computer Engineering University of Illinois at Urbana-Champaign, USA Distinguished Amrita Professor of Engineering Amrita Vishwa Vidyapeetham, India

Program for Hyderabad Area and Andhra Pradesh Faculty Sponsored by IEEE Hyderabad Section, IETE Hyderabad Center, and Vasavi College of Engineering IETE Conference Hall, Osmania University Campus Hyderabad, Andhra Pradesh June 3 – June 11, 2009 Workshop for Master Trainer Faculty Sponsored by IUCEE (Indo-US Coalition for Engineering Education) Infosys Campus, Mysore, Karnataka June 22 – July 3, 2009

2 Module 3 Maxwell’s Equations in Differential Form 3. 1 Faraday’s law and Ampere’s Circuital Law 3. 2 Gauss’ Laws and the Continuity Equation 3. 3 Curl and Divergence

3 Instructional Objectives 16. Obtain the simplified forms of Faraday’s law and Ampere’s circuital law in differential forms for any special cases of electric and magnetic fields, respectively, or the particular differential equation that satisfies both laws for a special case of electric or magnetic field 17. Determine if a given time-varying electric/magnetic field satisfies Maxwell’s curl equations, and if so find the corresponding magnetic/electric field, and any required condition, if the field is incompletely specified 18. Find the magnetic field due to one-dimensional static current distribution using Maxwell’s curl equation for the magnetic field 19. Find the electric field due to one-dimensional static charge distribution using Maxwell’s divergence equation for the electric field

4 Instructional Objectives (Continued) 20. Establish the physical realizability of a static electric field by using Maxwell’s curl equation for the static case, and of a magnetic field by using the Maxwell’s divergence equation for the magnetic field 21. Investigate qualitatively the curl and divergence of a vector field by using the curl meter and divergence meter concepts, respectively 22. Apply Stokes’ and divergence theorems in carrying out vector calculus manipulations

5 3. 1 Faraday’s Law and Ampère’s Circuital Law (EEE, Sec. 3. 1; FEME, Secs. 3. 1, 3. 2)

6 Maxwell’s Equations in Differential Form Why differential form? Because for integral forms to be useful, an a priori knowledge of the behavior of the field to be computed is necessary. The problem is similar to the following: There is no unique solution to this.

3 -7 However, if, e. g. , y(x) = Cx, then we can find y(x), since then On the other hand, suppose we have the following problem: Then y(x) = 2 x + C Thus the solution is unique to within a constant.

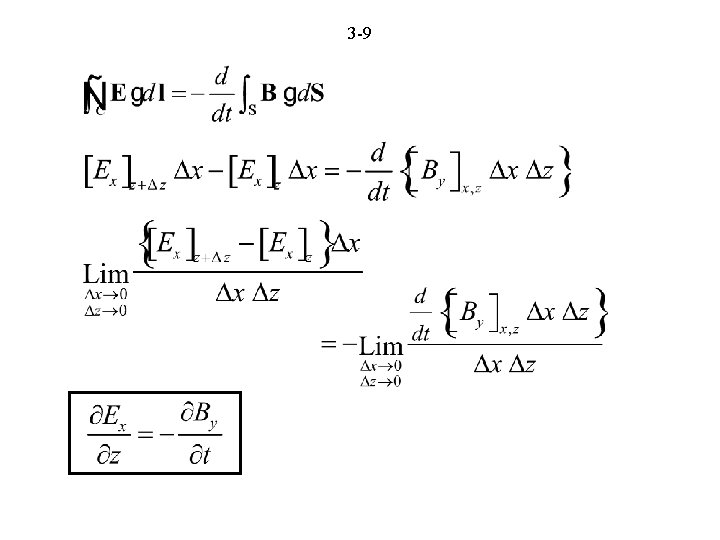
3 -8 FARADAY’S LAW First consider the special case and apply the integral form to the rectangular path shown, in the limit that the rectangle shrinks to a point.

3 -9

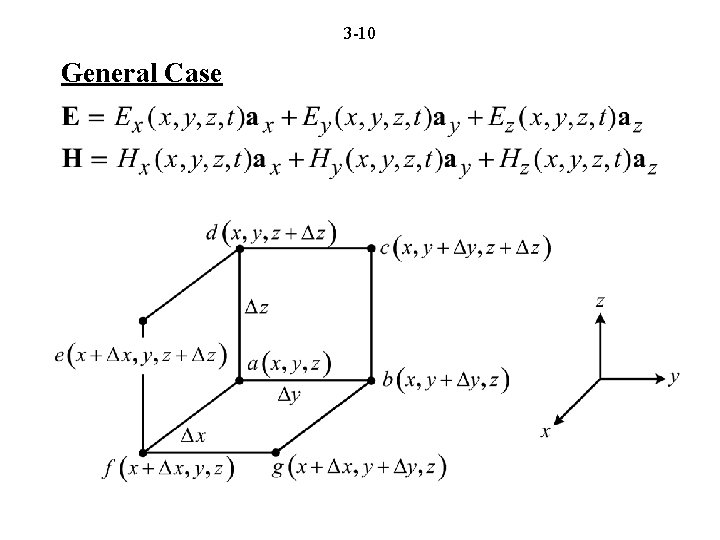
3 -10 General Case

3 -11 Lateral space derivatives of the components of E Time derivatives of the components of B

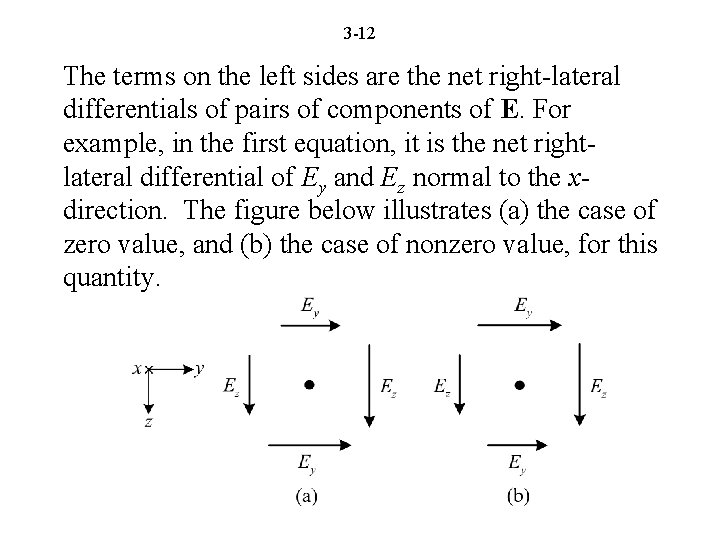
3 -12 The terms on the left sides are the net right-lateral differentials of pairs of components of E. For example, in the first equation, it is the net rightlateral differential of Ey and Ez normal to the xdirection. The figure below illustrates (a) the case of zero value, and (b) the case of nonzero value, for this quantity.

3 -13 Combining into a single differential equation, Differential form of Faraday’s Law

3 -14 AMPÈRE’S CIRCUITAL LAW Consider the general case first. Then noting that we obtain from analogy,

3 -15 Thus Special case: Differential form of Ampère’s circuital law
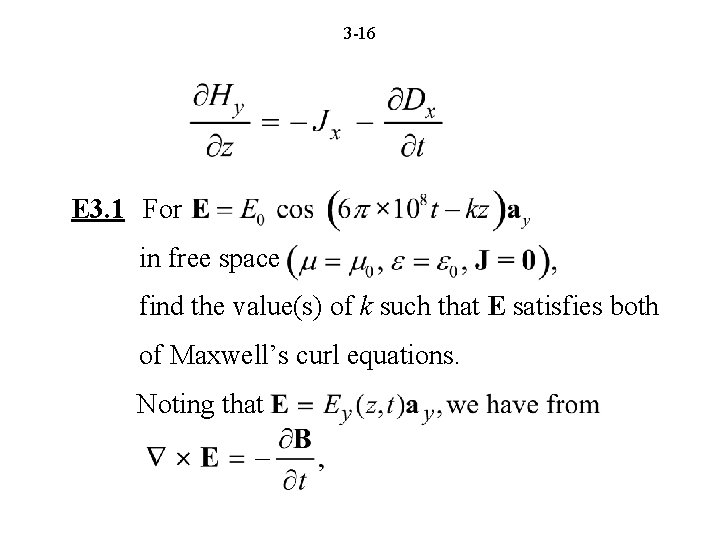
3 -16 E 3. 1 For in free space find the value(s) of k such that E satisfies both of Maxwell’s curl equations. Noting that
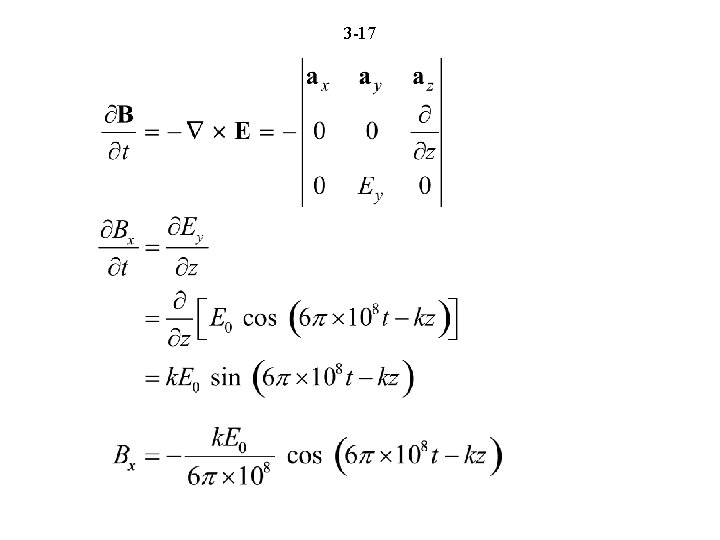
3 -17

3 -18 Thus, Then, noting that we have from

3 -19
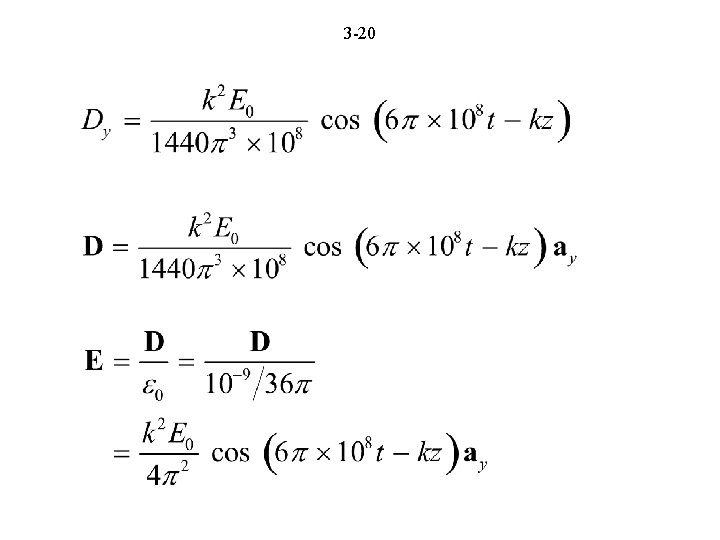
3 -20

3 -21 Comparing with the original given E, we have Sinusoidal traveling waves in free space, propagating in the z directions with velocity,

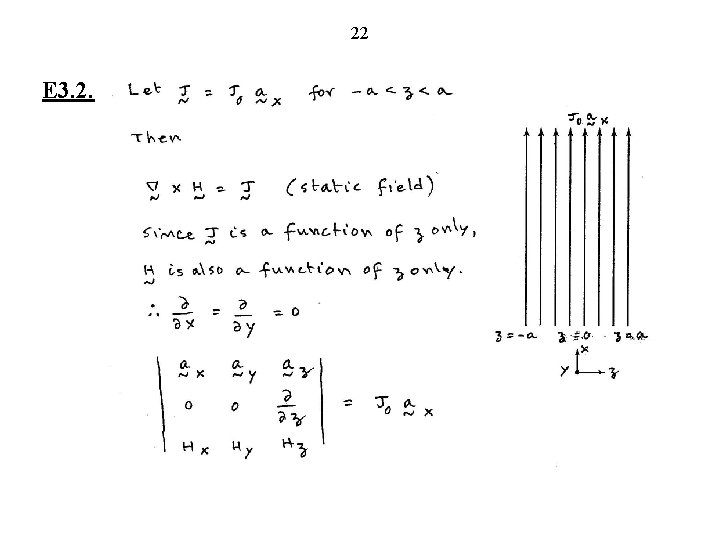
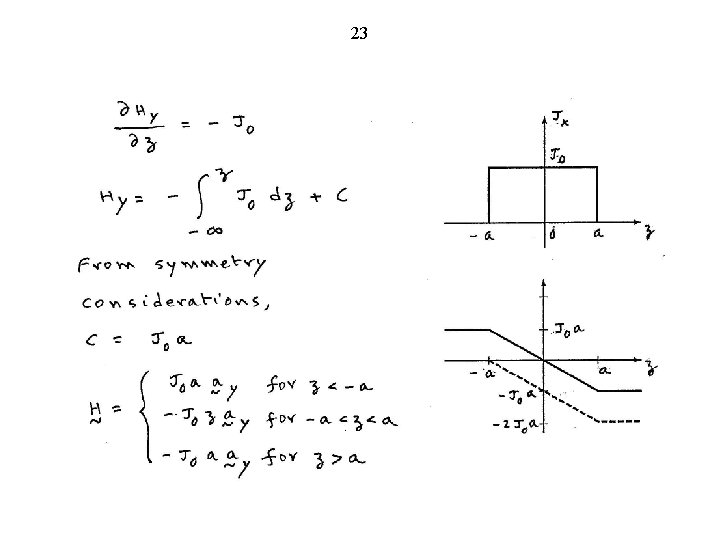
22 E 3. 2.

23

24 Review Questions 3. 1. Discuss the applicability of integral forms of Maxwell’s equations versus that of the differential forms for obtaining the solutions for the fields. 3. 2. State Faraday’s law in differential form for the special case of E = Ex(z, t)ax and H = Hy(z, t)ay. How is it derived from Faraday’s law in integral form? 3. 3. How would you derive Faraday’s law in differential form from its integral form for the general case of an arbitrary electric field? 3. 4. What is meant by the net right-lateral differential of the x- and y- components of a vector normal to the z direction? Give an example in which the net right-lateral differential of Ex and Ey normal to the z-direction is zero, although the individual derivatives are nonzero. 3. 5. What is the determinant expansion for the curl of a vector in Cartesian coordinates?

25 Review Questions (Continued) 3. 6. State Ampere’s circuital law in differential form for the general case of an arbitrary magnetic field. How is it obtained from its integral form? 3. 7. State Ampere’s circuital law in differential form for the special case of H = Hy(z, t)ay. How is it derived from the Ampere’s circuital law for the general case in differential form? 3. 8. If a pair of E and B at a point satisfies Faraday’s law in differential form, does it necessarily follow that it also satisfies Ampere’s circuital form and vice versa? 3. 9. Discuss the determination of magnetic field for one dimensional current distributions, in the static case, using Ampere’s circuital law in differential form, without the displacement current density term.

26 Problem S 3. 1. Obtaining the differential equation for a special case that satisfies both of Maxwell’s curl equations

27 Problem S 3. 2. Finding possible condition for a specified field to satisfy both of Maxwell’s curl equations

28 Problem S 3. 3. Magnetic field due to a one-dimensional current distribution for the static case

29 Problem S 3. 3. Magnetic field due to a one-dimensional current distribution for the static case (Continued)

30 Problem S 3. 3. Magnetic field due to a one-dimensional current distribution for the static case (Continued)

31 3. 2 Gauss’ Laws and the Continuity Equation (EEE, Sec. 3. 2; FEME, Secs. 3. 4, 3. 5, 3. 6)

3 -32 GAUSS’ LAW FOR THE ELECTRIC FIELD
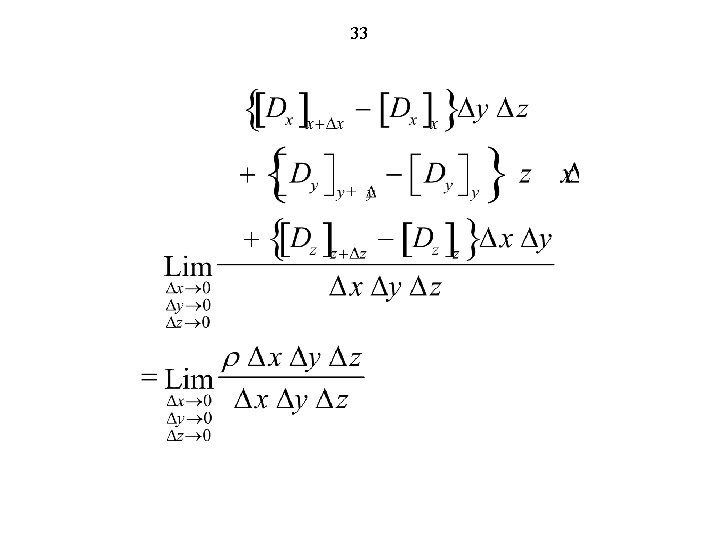
33

3 -34 The quantity on the left side is the net longitudinal differential of the components of D, that is, the algebraic sum of the derivatives of components of D along their respective directions. It can be written as which is known as the “divergence of D. ” Thus, the equation becomes

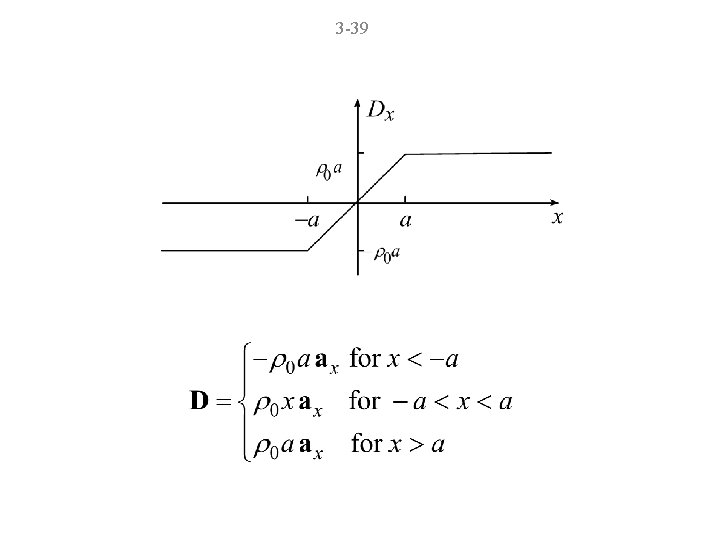
3 -35 The figure below illustrates the case of (a) zero value, and (b) nonzero value for . E 3. 3 Given that Find D everywhere.

3 -36 Noting that = (x) and hence D = D(x), we set

3 -37 Thus, which also means that D has only an xcomponent. Proceeding further, we have where C is the constant of integration. Evaluating the integral graphically, we have the following:

3 -38 0 From symmetry considerations, the fields on the two sides of the charge distribution must be equal in magnitude and opposite in direction. Hence, C = – 0 a

3 -39

40 GAUSS’ LAW FOR THE MAGNETIC FIELD From analogy Solenoidal property of magnetic field lines. Provides test for physical realizability of a given vector field as a magnetic field.

3 -41 LAW OF CONSERVATION OF CHARGE Continuity Equation

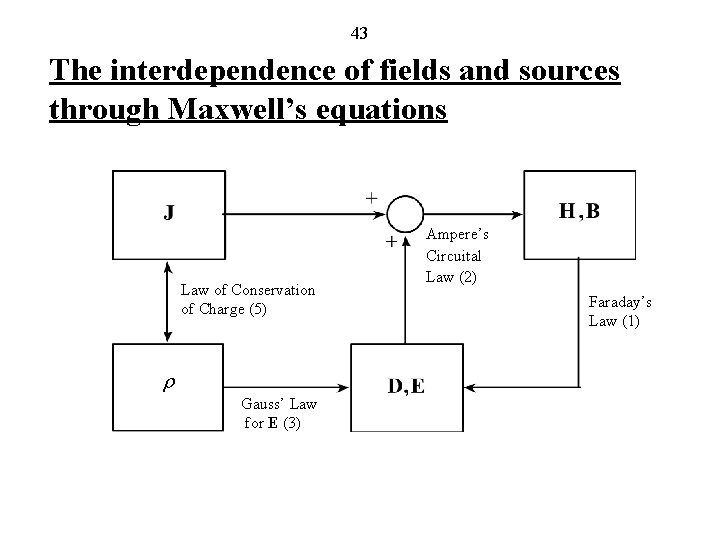
3 -42 SUMMARY (1) (2) (3) (4) (5) (4) is, however, not independent of (1), and (3) can be derived from (2) with the aid of (5).

43 The interdependence of fields and sources through Maxwell’s equations Law of Conservation of Charge (5) Gauss’ Law for E (3) Ampere’s Circuital Law (2) Faraday’s Law (1)

44 Review Questions 3. 10. State Gauss’ law for the electric field in differential form. How is it derived from its integral form? 3. 11. What is meant by the net longitudinal differential of the components of a vector field? Give an example in which the net longitudinal differential of the components of a vector field is zero, although the individual derivatives are nonzero. 3. 12. What is the expression for the divergence of a vector in Cartesian coordinates? 3. 13. Discuss the determination of electric field for one dimensional charge distributions, in the static case, using Gauss’ law for the electric field in differential form.

45 Review Questions (Continued) 3. 14. State Gauss’ law for the magnetic field in differential form. How is it obtained from its integral form? 3. 15. How can you determine if a given vector field can be realized as a magnetic field? 3. 16. State the continuity equation. 3. 17. Summarize Maxwell’s equations in differential form and the continuity equation, stating which of the equations are independent. 3. 18. Discuss the interdependence of fields and sources through Maxwell’s equations.

46 Problem S 3. 4. Finding the electric field due to a onedimensional charge distribution for the static case

47 Problem S 3. 5. Finding the condition for the realizability of a specified vector field as a certain type of field

48 Problem S 3. 6. Determination of the group belonging to a specified vector field, based on its physical realizability

49 3. 3 Curl and Divergence (EEE, Sec. 3. 3, App. B ; FEME, Secs. 3. 3 and 3. 6, App. B)

3 -50 Maxwell’s Equations in Differential Form Curl Divergence

3 -51 Curl and Divergence in Cylindrical Coordinates

52 Curl and Divergence in Spherical Coordinates

3 -53 Basic definition of curl is the maximum value of circulation of A per unit area in the limit that the area shrinks to the point. Direction of is the direction of the normal vector to the area in the limit that the area shrinks to the point, and in the right-hand sense.

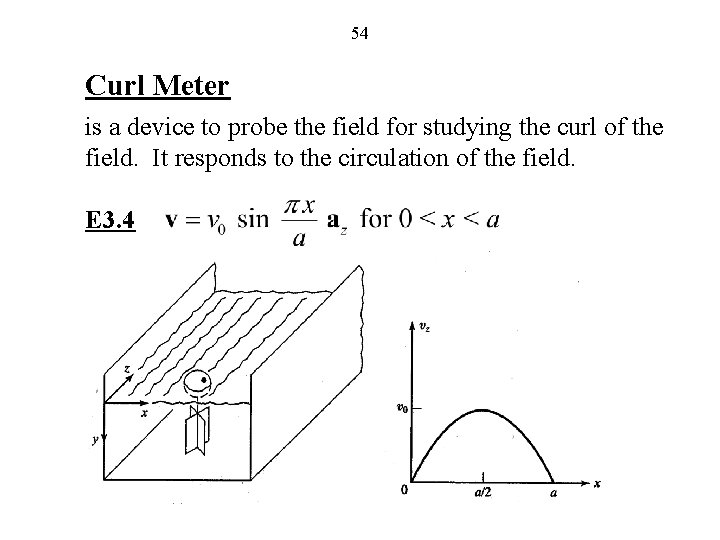
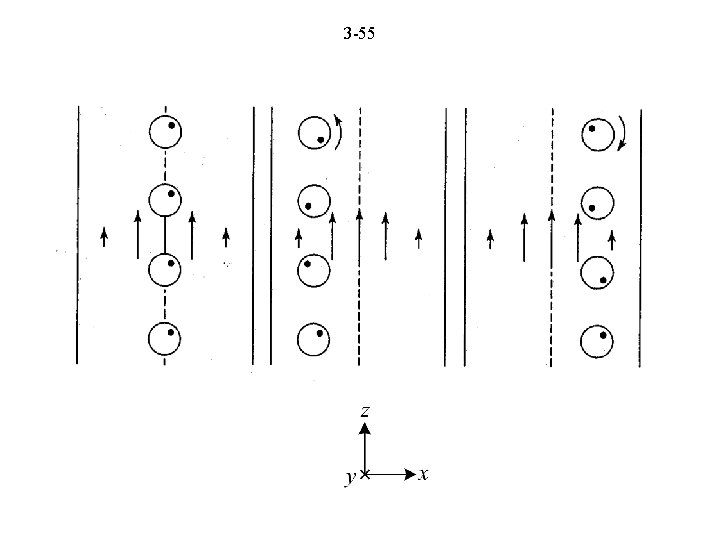
54 Curl Meter is a device to probe the field for studying the curl of the field. It responds to the circulation of the field. E 3. 4

3 -55
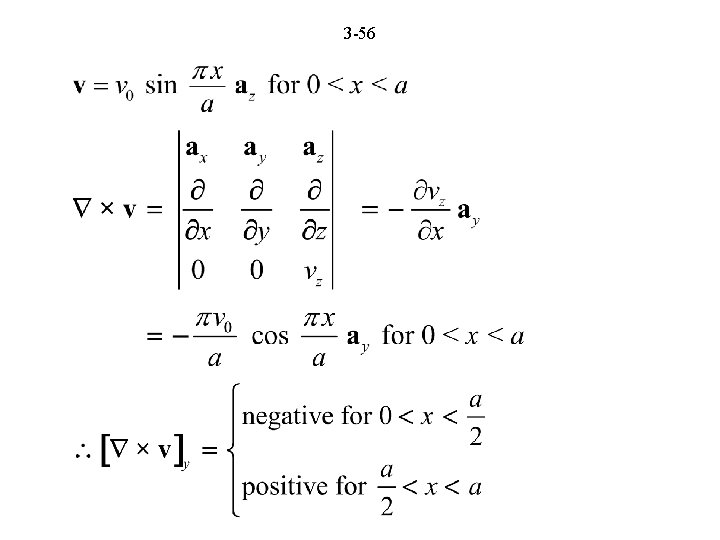
3 -56

57 Basic definition of divergence is the outward flux of A per unit volume in the limit that the volume shrinks to the point. Divergence meter is a device to probe the field for studying the divergence of the field. It responds to the closed surface integral of the vector field.

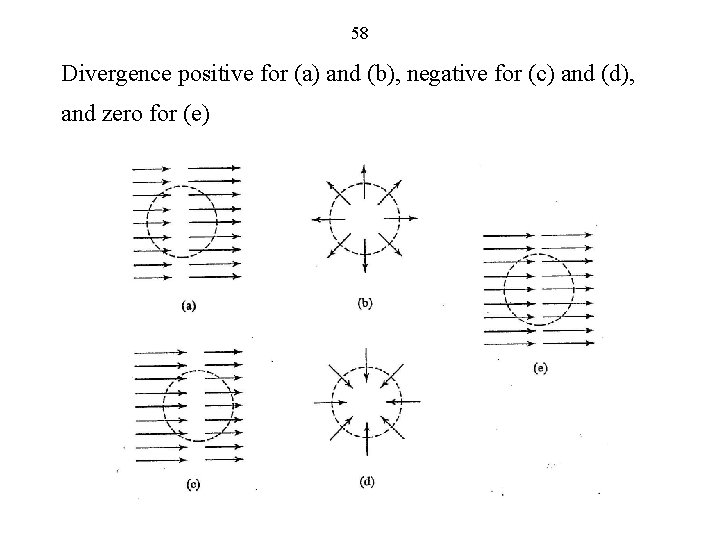
58 Divergence positive for (a) and (b), negative for (c) and (d), and zero for (e)

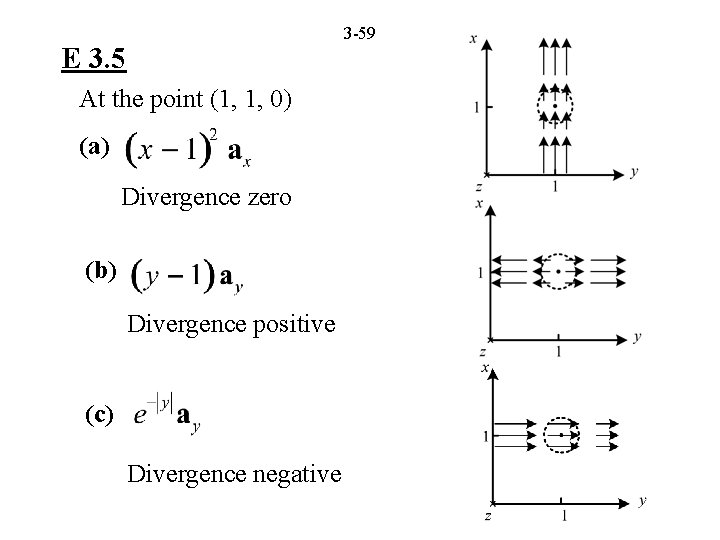
3 -59 E 3. 5 At the point (1, 1, 0) (a) Divergence zero (b) Divergence positive (c) Divergence negative

60 Two Useful Theorems: Stokes’ theorem Divergence theorem A useful identity
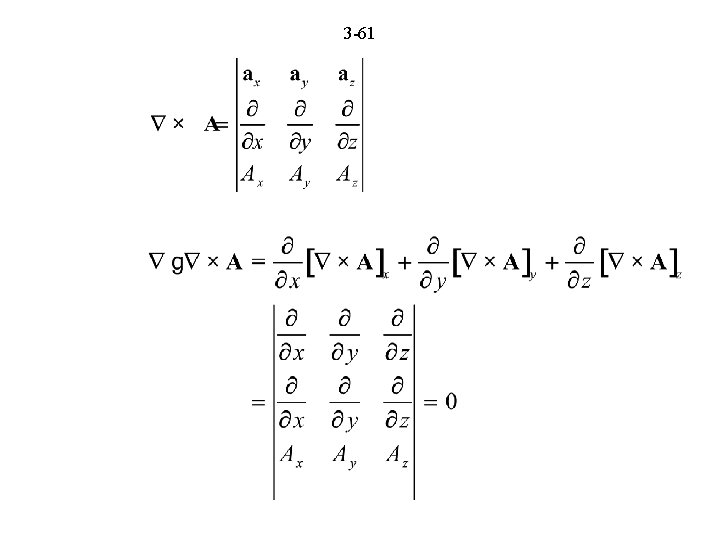
3 -61

62 Review Questions 3. 19. State and briefly discuss the basic definition of the curl of a vector. 3. 20. What is a curl meter? How does it help visualize the behavior of the curl of a vector field? 3. 21. Provide two examples of physical phenomena in which the curl of the vector field is nonzero. 3. 22. State and briefly discuss the basic definition of the divergence of a vector. 3. 23. What is a divergence meter? How does it help visualize the behavior of the divergence of a vector field? 3. 24. Provide two examples of physical phenomena in which the divergence of the vector field is nonzero.

63 Review Questions (Continued) 3. 25. State Stokes’ theorem and discuss its application. 3. 26. State the divergence theorem and discuss its application. 3. 27. What is the divergence of the curl of a vector?

64 Problem S 3. 7. Investigation of the behavior of the curl of a vector field for different cases

65 Problem S 3. 8. Investigation of the behavior of the divergence of a vector field for different cases

66 Problem S 3. 9. Verification of Stokes’ theorem and an application of the divergence theorem

67 Problem S 3. 9. Verification of Stokes’ theorem and an application of the divergence theorem (Continued)

The End