FUNDAMENTALS OF ELECTRICAL ENGINEERING ENT 163 LECTURE 5

FUNDAMENTALS OF ELECTRICAL ENGINEERING [ ENT 163 ] LECTURE #5 a CAPACITORS AND INDUCTORS HASIMAH ALI Programme of Mechatronics, School of Mechatronics Engineering, Uni. MAP. Email: hashimah@unimap. edu. my

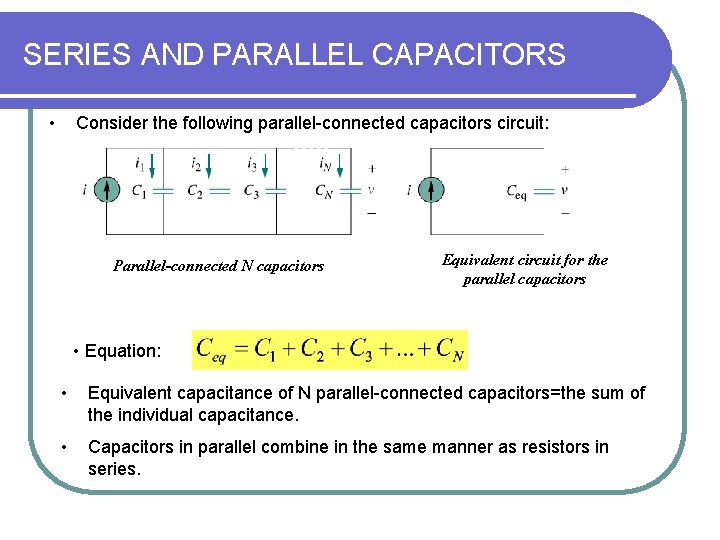
SERIES AND PARALLEL CAPACITORS • Consider the following parallel-connected capacitors circuit: Parallel-connected N capacitors Equivalent circuit for the parallel capacitors • Equation: • Equivalent capacitance of N parallel-connected capacitors=the sum of the individual capacitance. • Capacitors in parallel combine in the same manner as resistors in series.

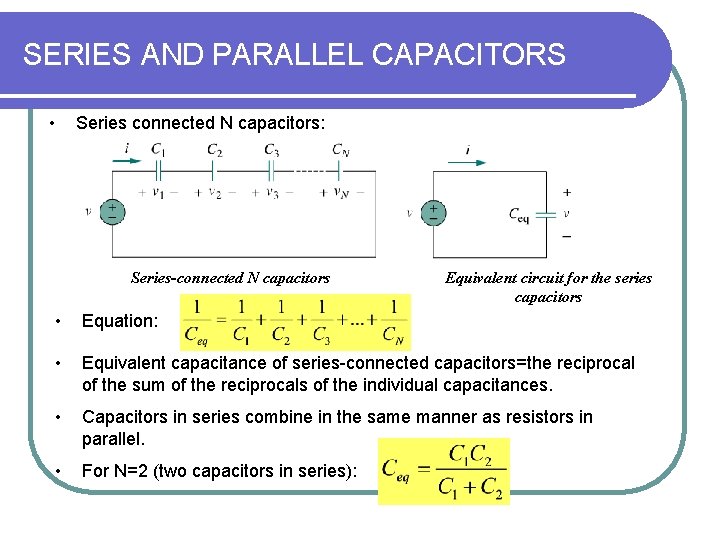
SERIES AND PARALLEL CAPACITORS • Series connected N capacitors: Series-connected N capacitors Equivalent circuit for the series capacitors • Equation: • Equivalent capacitance of series-connected capacitors=the reciprocal of the sum of the reciprocals of the individual capacitances. • Capacitors in series combine in the same manner as resistors in parallel. • For N=2 (two capacitors in series):

SERIES AND PARALLEL CAPACITORS Example: Find the equivalent capacitance seen between terminals a and b of the circuit shown.

SERIES AND PARALLEL CAPACITORS Example: Find the voltage across each capacitor.

SERIES AND PARALLEL CAPACITORS Solution: Equivalent capacitance:

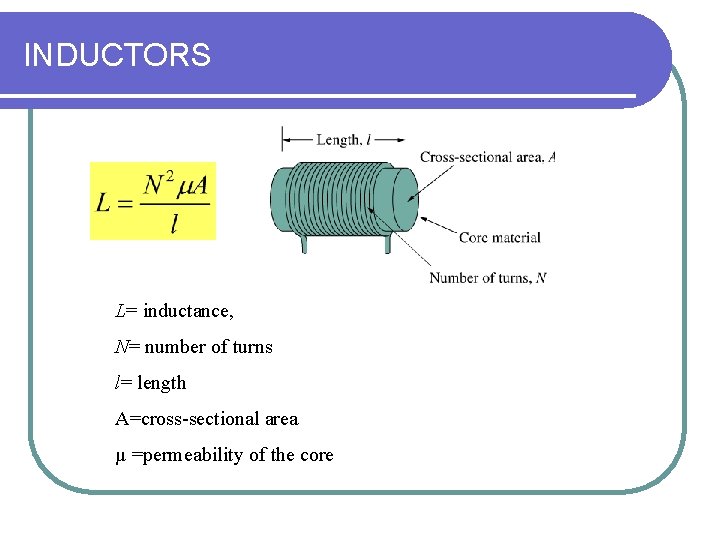
INDUCTORS • Inductor – passive element designed to store energy in its magnetic field. • Used in power supplies, transformers, radios, TVs, radars, electric motors. • An inductor consists of a coil of conducting wire. • Inductance is the property whereby an inductor exhibits oppositions to the change flowing through it, measured in henrys (H). • Inductance of an inductor – depends on its physical dimension and construction.

INDUCTORS L= inductance, N= number of turns l= length A=cross-sectional area µ =permeability of the core

INDUCTORS • Inductors – may be fixed or variable • Practically, core – iron steel, plastic, air.

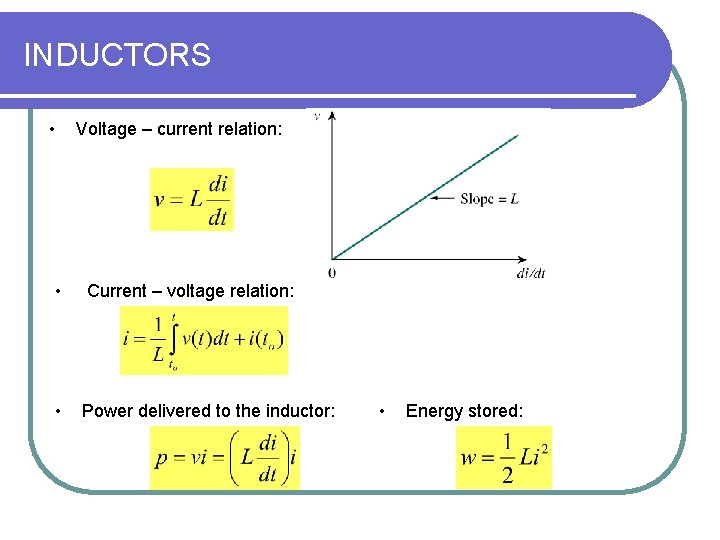
INDUCTORS • Voltage – current relation: • Current – voltage relation: • Power delivered to the inductor: • Energy stored:

INDUCTORS 1. Important properties: 1. Voltage across an inductor is zero when the current is constant. An inductor acts like a short circuit to dc. 2. An important property of the inductor is its opposition to the change in current flowing through it. The current through an inductor cannot change instantaneously.

INDUCTORS 1. Like the ideal capacitor, the ideal inductor does not dissipate energy. 2. A practical, nonideal inductor has a significant resistive component, due to the fact that the inductor is made of a conducting material such as copper, which has some resistance Rw. It is also has a winding capacitance Cw due to the capacitive coupling between the conducting coils. Since both values are very small, they can be ignored in most cases.

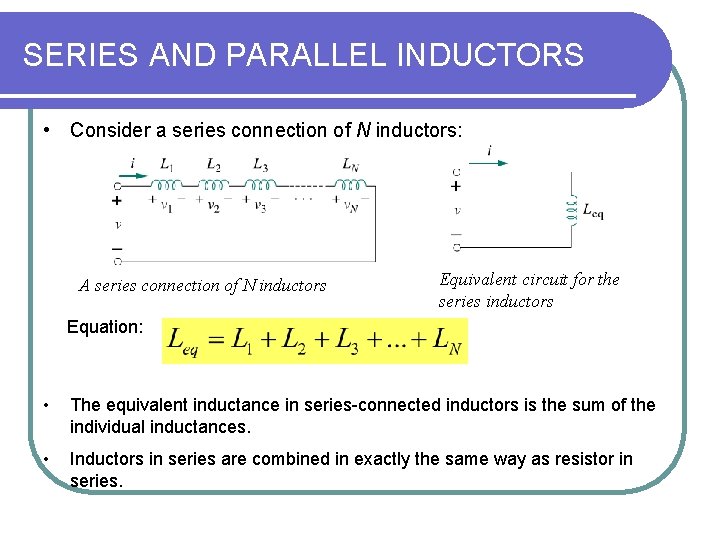
SERIES AND PARALLEL INDUCTORS • Consider a series connection of N inductors: A series connection of N inductors Equivalent circuit for the series inductors Equation: • The equivalent inductance in series-connected inductors is the sum of the individual inductances. • Inductors in series are combined in exactly the same way as resistor in series.

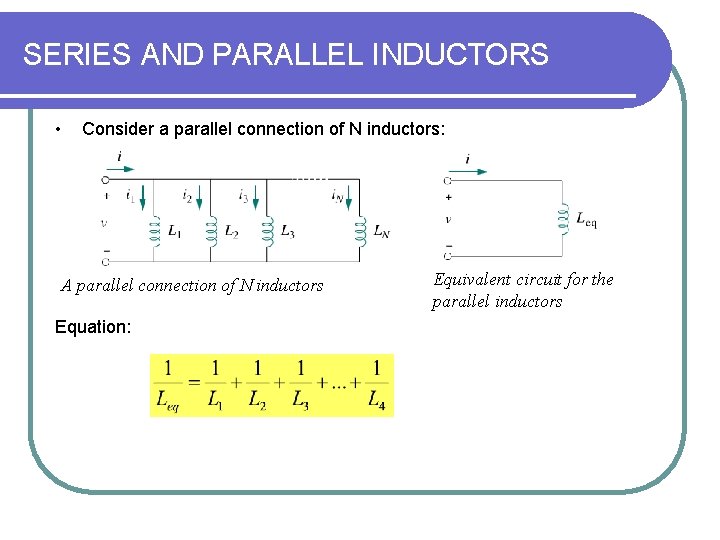
SERIES AND PARALLEL INDUCTORS • Consider a parallel connection of N inductors: A parallel connection of N inductors Equation: Equivalent circuit for the parallel inductors

SERIES AND PARALLEL INDUCTORS • The equivalent inductance of parallel inductors is the reciprocal of the sum of the reciprocals of the individual inductances • The inductors in parallel are combined in the same way as resistors in parallel. • For two inductors in parallel (N=2)

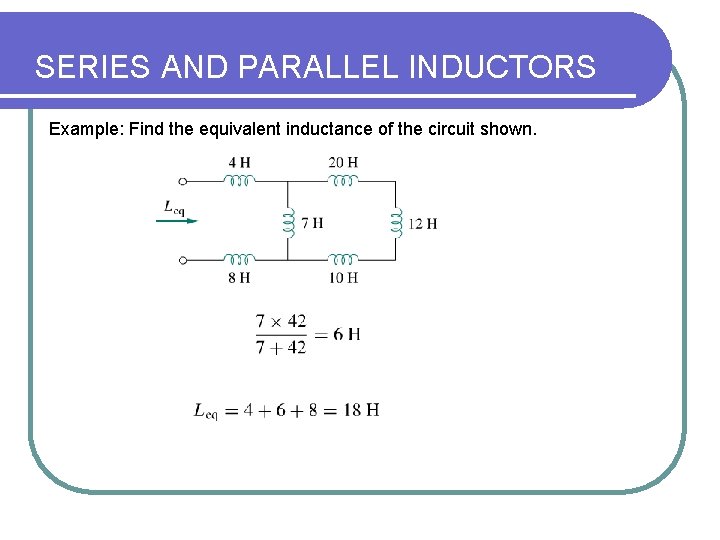
SERIES AND PARALLEL INDUCTORS Example: Find the equivalent inductance of the circuit shown.

SERIES AND PARALLEL INDUCTORS Example:

SERIES AND PARALLEL INDUCTORS Solution:

Further Reading 1. Fundamentals of Electric Circuits, 2 nd Edition, Mc. Grawhill Alexander, C. K. and Sadiku, M. N. O. 2. Electric Circuit, 8 th Edition, Pearson, Nillson and Riedel. 3. Circuits, Brooks/ Cole, A. Bruce Carlson. 4. http: //www. scribd. com/word/full/2031941? access_key=key 1 vybbz 6 deqeinoosecmm