Fundamentals of Digital Signal Processing Fourier Transform of

Fundamentals of Digital Signal Processing

Fourier Transform of continuous time signals with t in sec and F in Hz (1/sec). Examples:

Discrete Time Fourier Transform of sampled signals with f the digital frequency (no dimensions). Example: since, using the Fourier Series,

Property of DTFT • f is the digital frequency and has no dimensions • is periodic with period f = 1. • we only define it on one period

Sampled Complex Exponential: no aliasing 1. No Aliasing digital frequency

Sampled Complex Exponential: aliasing 2. Aliasing digital frequency

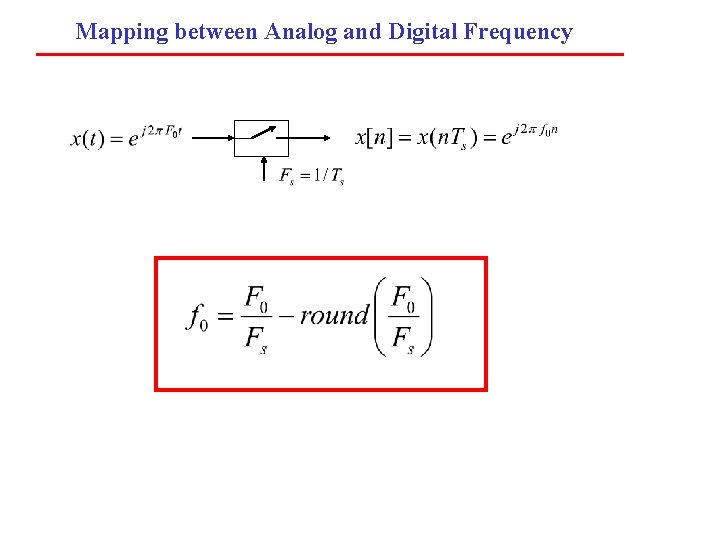
Mapping between Analog and Digital Frequency

Example Then: • analog frequency • FT: • digital frequency • DTFT: for

Example Then: • analog frequency • FT: • digital frequency • DTFT: for

Example Then: • analog frequencies • FT: • digital frequencies • DTFT

Linear Time Invariant (LTI) Systems and z-Transform If the system is LTI we compute the output with the convolution: If the impulse response has a finite duration, the system is called FIR (Finite Impulse Response):

Z-Transform Facts: Frequency Response of a filter:

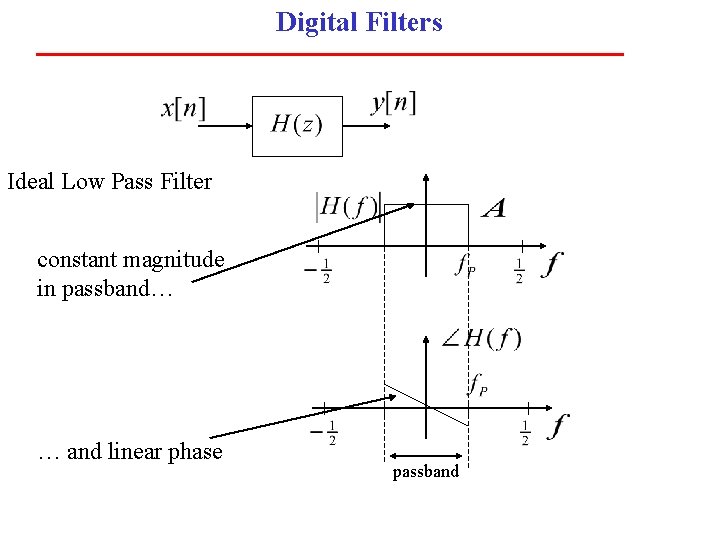
Digital Filters Ideal Low Pass Filter constant magnitude in passband… … and linear phase passband

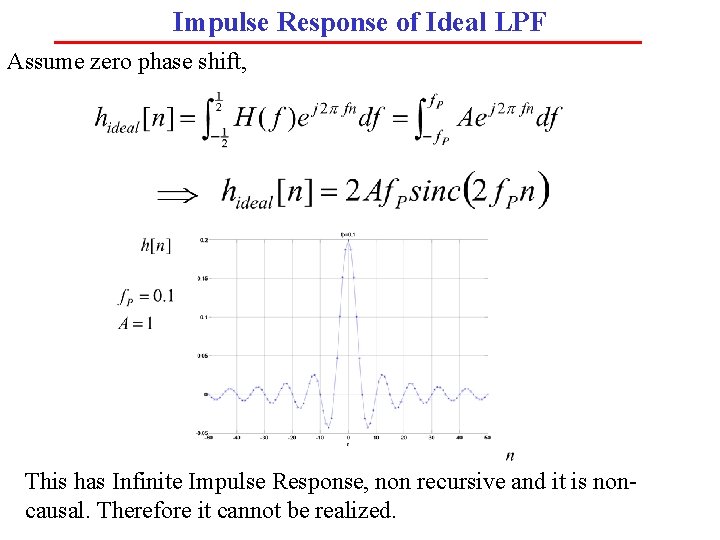
Impulse Response of Ideal LPF Assume zero phase shift, This has Infinite Impulse Response, non recursive and it is noncausal. Therefore it cannot be realized.

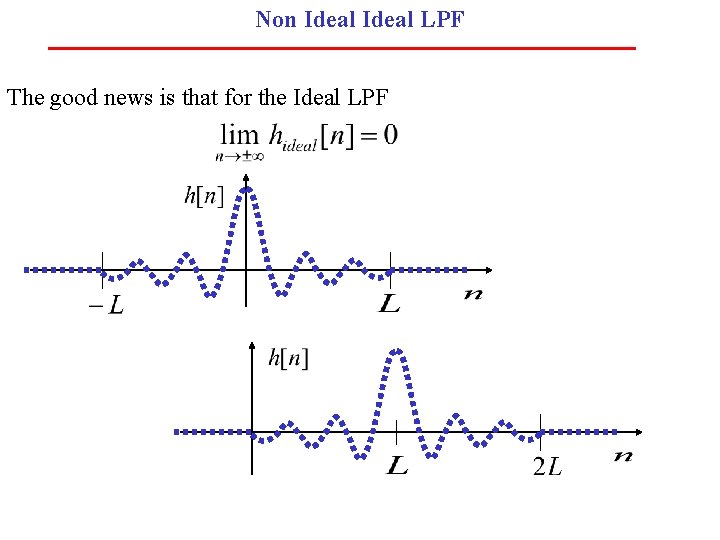
Non Ideal LPF The good news is that for the Ideal LPF

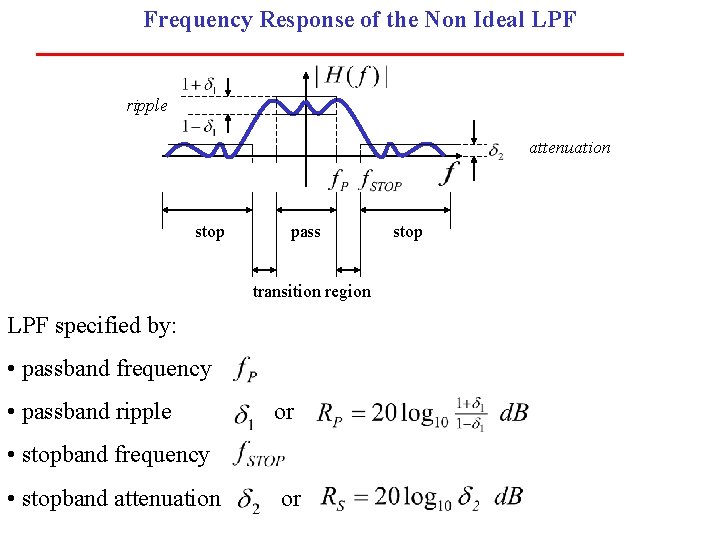
Frequency Response of the Non Ideal LPF ripple attenuation stop pass transition region LPF specified by: • passband frequency • passband ripple or • stopband frequency • stopband attenuation or stop

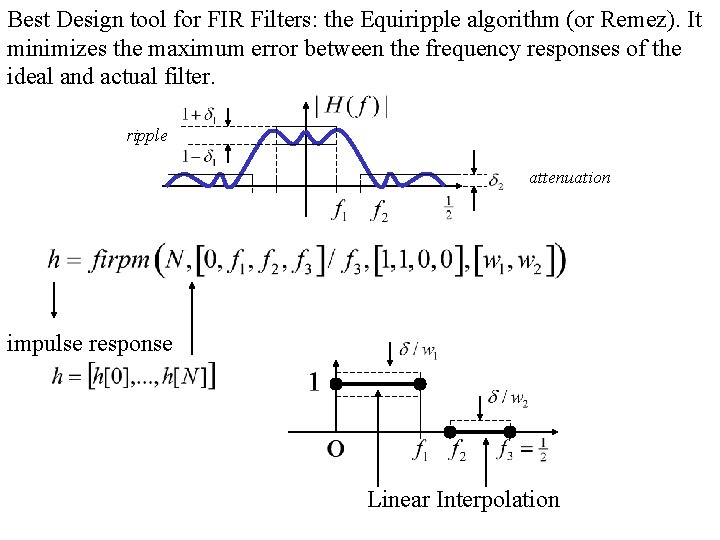
Best Design tool for FIR Filters: the Equiripple algorithm (or Remez). It minimizes the maximum error between the frequency responses of the ideal and actual filter. ripple attenuation impulse response Linear Interpolation

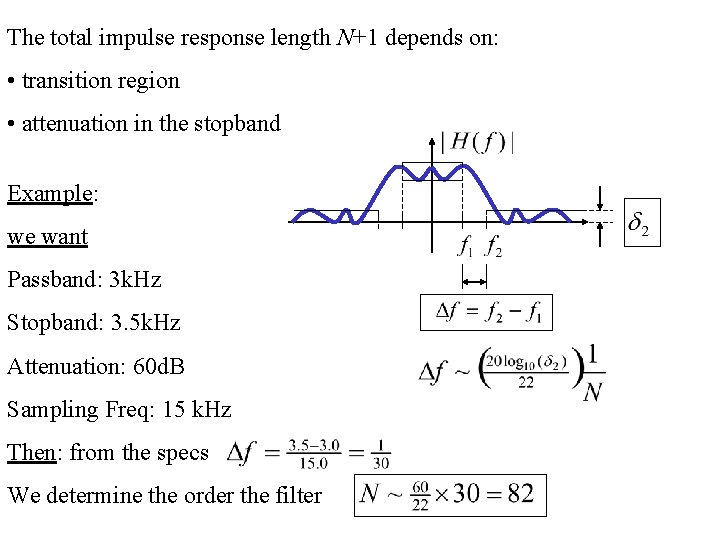
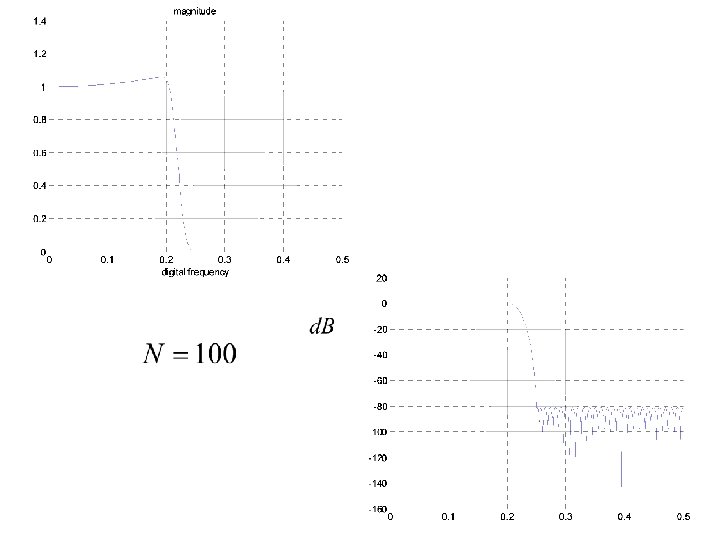
The total impulse response length N+1 depends on: • transition region • attenuation in the stopband Example: we want Passband: 3 k. Hz Stopband: 3. 5 k. Hz Attenuation: 60 d. B Sampling Freq: 15 k. Hz Then: from the specs We determine the order the filter

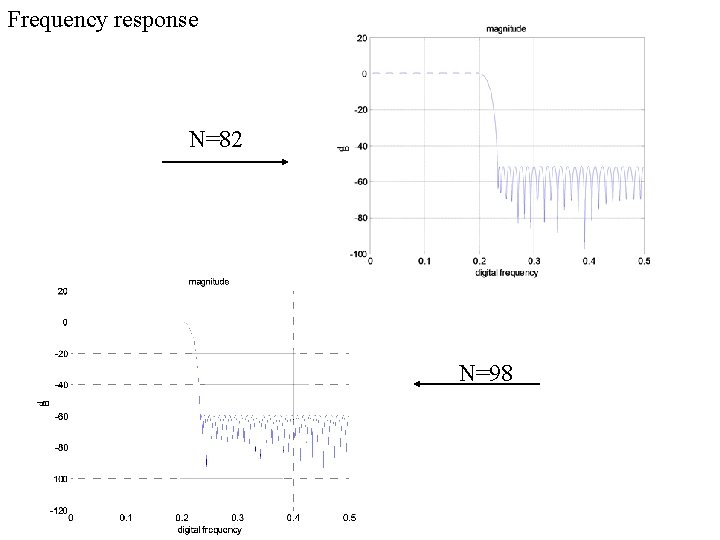
Frequency response N=82 N=98

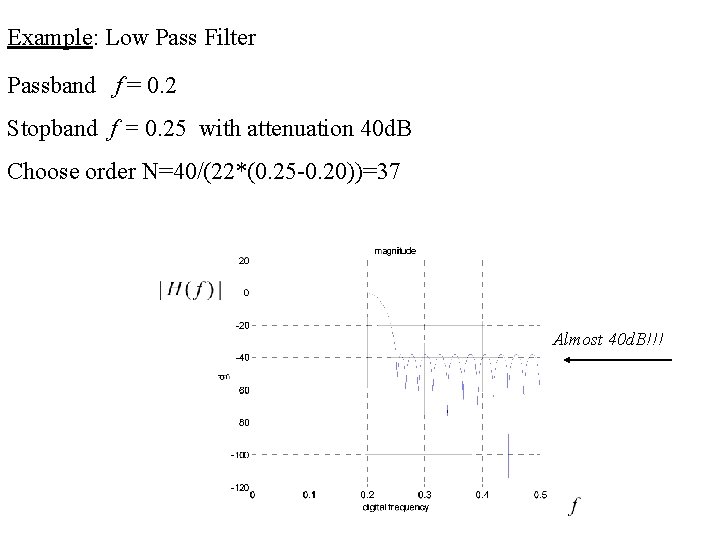
Example: Low Pass Filter Passband f = 0. 2 Stopband f = 0. 25 with attenuation 40 d. B Choose order N=40/(22*(0. 25 -0. 20))=37 Almost 40 d. B!!!

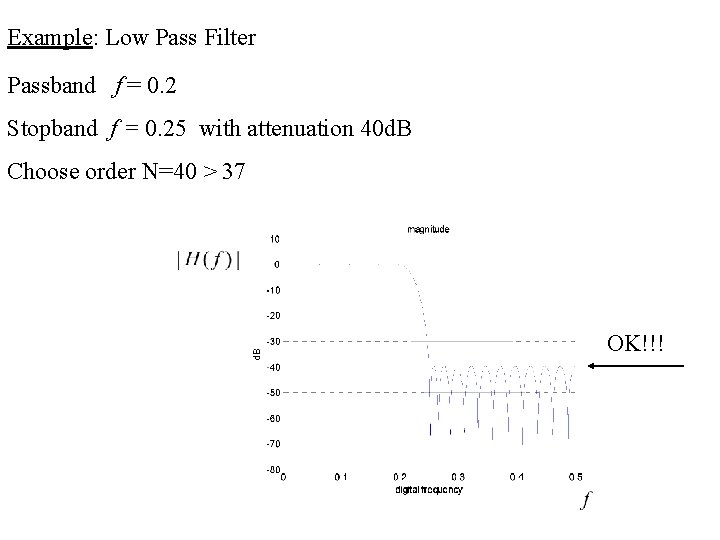
Example: Low Pass Filter Passband f = 0. 2 Stopband f = 0. 25 with attenuation 40 d. B Choose order N=40 > 37 OK!!!

General FIR Filter of arbitrary Frequency Response Weights for Error: Then apply: … and always check frequency response if it is what you expect!

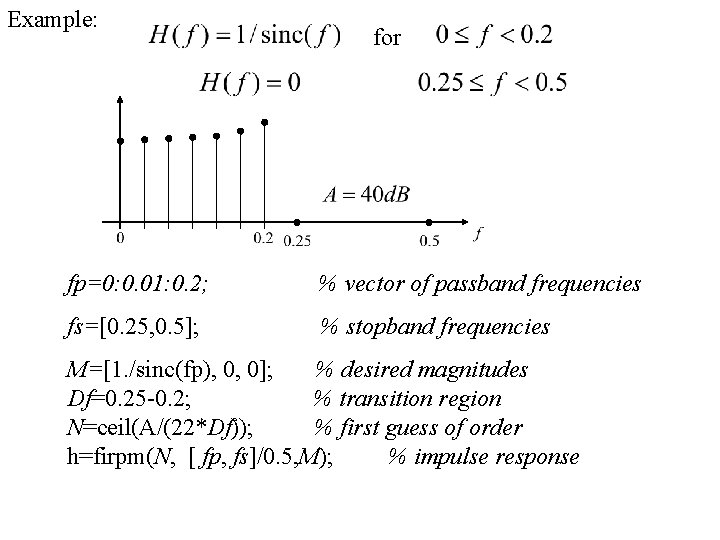
Example: for fp=0: 0. 01: 0. 2; % vector of passband frequencies fs=[0. 25, 0. 5]; % stopband frequencies M=[1. /sinc(fp), 0, 0]; % desired magnitudes Df=0. 25 -0. 2; % transition region N=ceil(A/(22*Df)); % first guess of order h=firpm(N, [ fp, fs]/0. 5, M); % impulse response

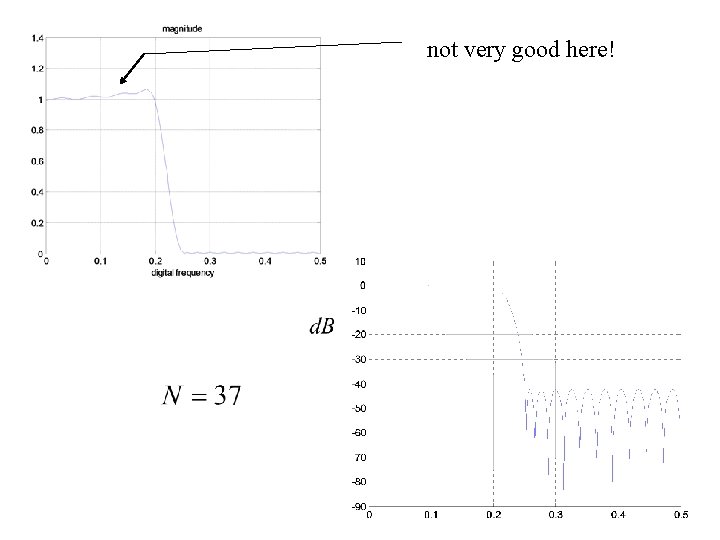
not very good here!

To improve it: 1. Increase order 2. Add weights w=[1*ones(1, length(fp)/2), 0. 2*ones(1, length(fs)/2)]; h=firpm(N, [fp, fs]/0. 5, M, w);