Fundamentals of dielectric response Polarization mechanisms centrosymmetric cubic

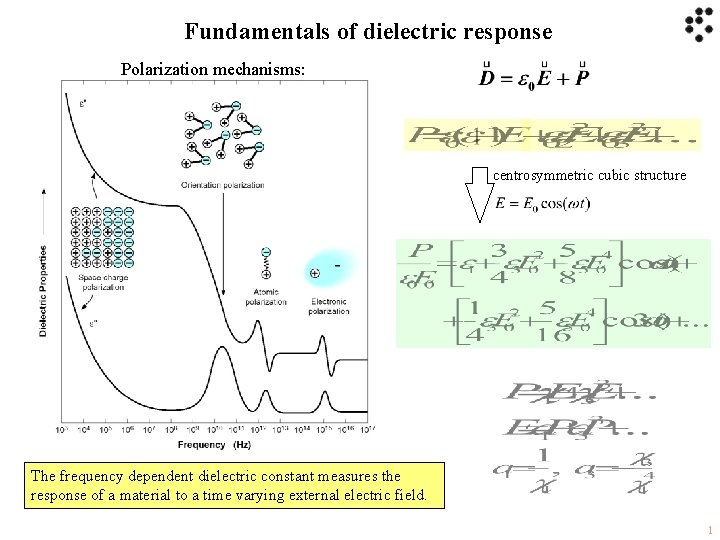
Fundamentals of dielectric response Polarization mechanisms: centrosymmetric cubic structure The frequency dependent dielectric constant measures the response of a material to a time varying external electric field. 1

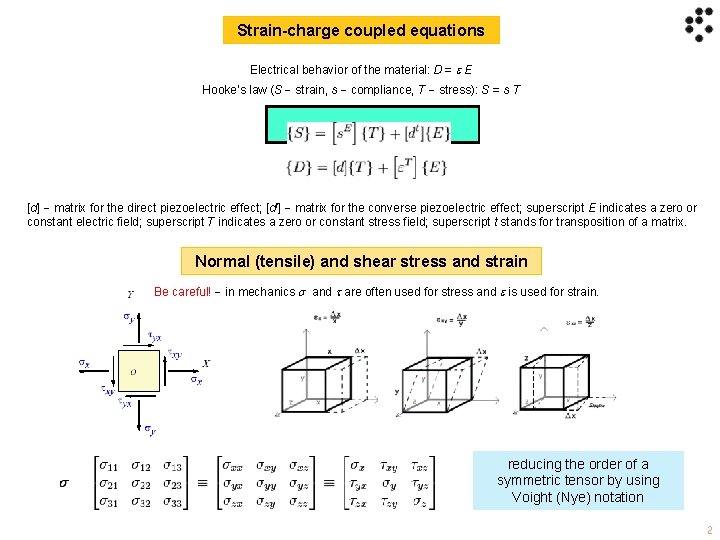
Strain-charge coupled equations Electrical behavior of the material: D = E Hooke‘s law (S strain, s compliance, T stress): S = s T [d] matrix for the direct piezoelectric effect; [dt] matrix for the converse piezoelectric effect; superscript E indicates a zero or constant electric field; superscript T indicates a zero or constant stress field; superscript t stands for transposition of a matrix. Normal (tensile) and shear stress and strain Be careful! in mechanics and are often used for stress and is used for strain. reducing the order of a symmetric tensor by using Voight (Nye) notation 2

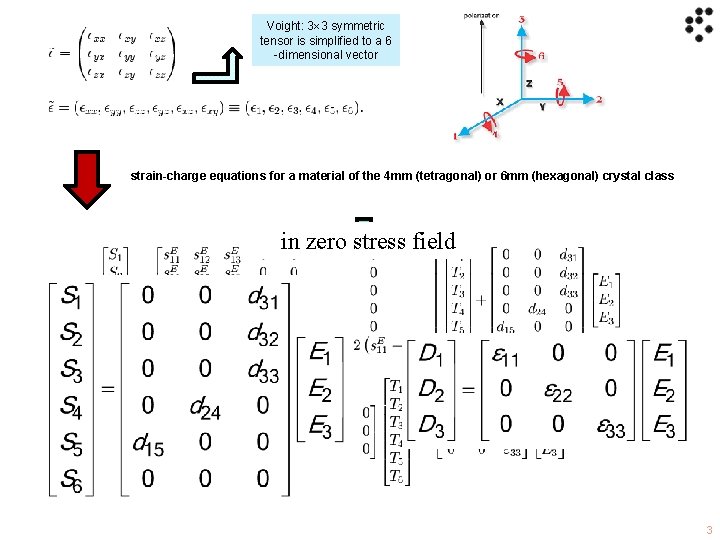
Voight: 3 3 symmetric tensor is simplified to a 6 -dimensional vector strain-charge equations for a material of the 4 mm (tetragonal) or 6 mm (hexagonal) crystal class in zero stress field 3

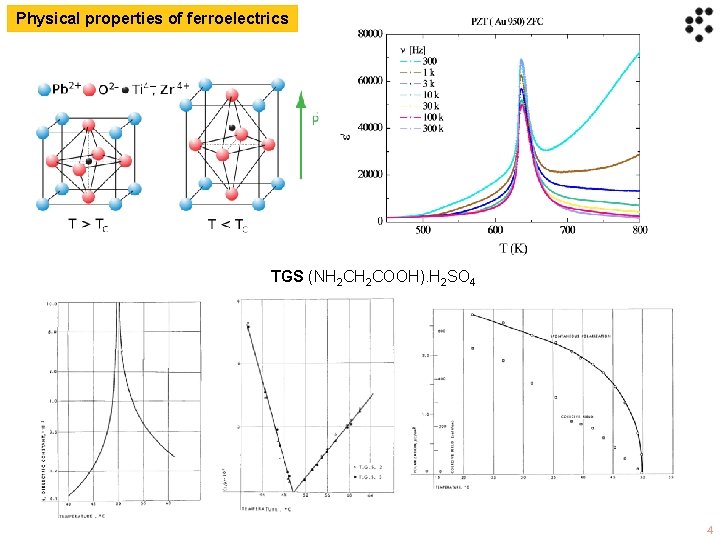
Physical properties of ferroelectrics TGS (NH 2 COOH). H 2 SO 4 4

Phenomenological description of ferroelectrics Landau theory of phase transitions thermodynamic potential takes the form of a power series in the order parameter: Minimum of the Landau potential the equilibrium value of the order parameter: Taking into account very general symmetry properties of the underlying Hamiltonian one can set a priori the qualitative behaviour of the coefficients in the series. The value of those coefficients then very generally define the nature of the phase transition, which may be found to be either first or second order ferroelectrics order parameter is polarization, free energy density contains only even terms (it must have the symmetry of the paraelectric phase which is invariant with respect to polarization reversal) minimization the stable solution corresponds to minimum in free energy in paraelectric phase (P 0 = 0) ; we know that ; thus 5

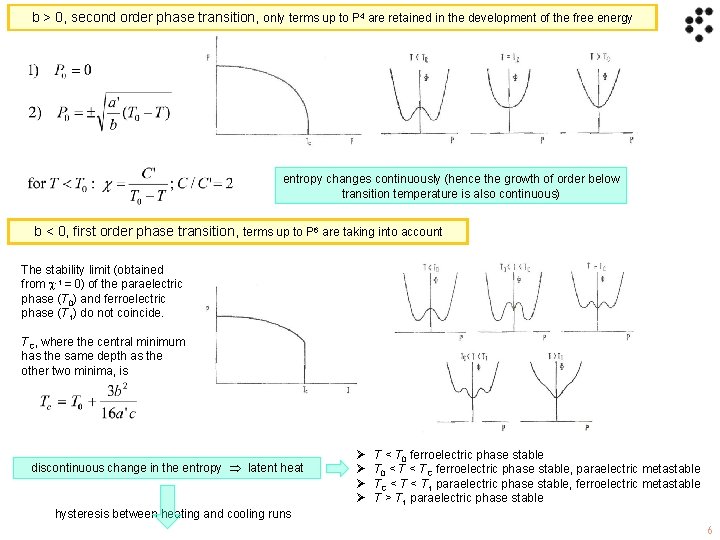
b > 0, second order phase transition, only terms up to P 4 are retained in the development of the free energy entropy changes continuously (hence the growth of order below transition temperature is also continuous) b < 0, first order phase transition, terms up to P 6 are taking into account The stability limit (obtained from -1 = 0) of the paraelectric phase (T 0) and ferroelectric phase (T 1) do not coincide. TC, where the central minimum has the same depth as the other two minima, is discontinuous change in the entropy latent heat Ø Ø T < T 0 ferroelectric phase stable T 0 < TC ferroelectric phase stable, paraelectric metastable TC < T 1 paraelectric phase stable, ferroelectric metastable T > T 1 paraelectric phase stable hysteresis between heating and cooling runs 6

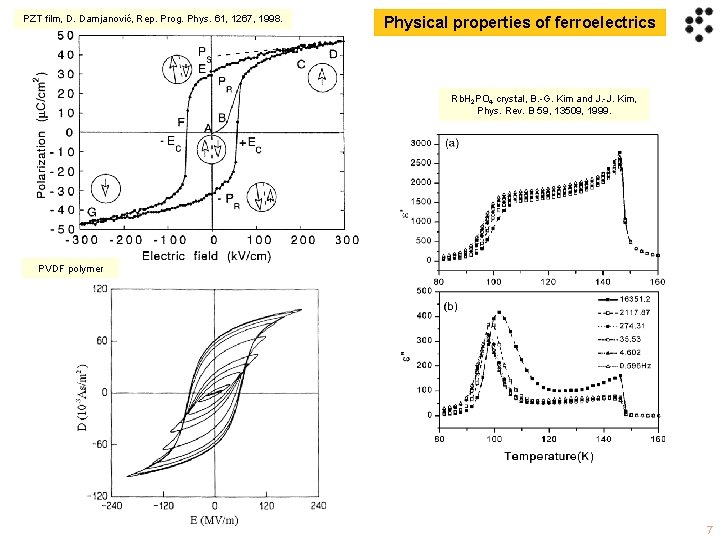
PZT film, D. Damjanović, Rep. Prog. Phys. 61, 1267, 1998. Physical properties of ferroelectrics Rb. H 2 PO 4 crystal, B. -G. Kim and J. -J. Kim, Phys. Rev. B 59, 13509, 1999. PVDF polymer 7

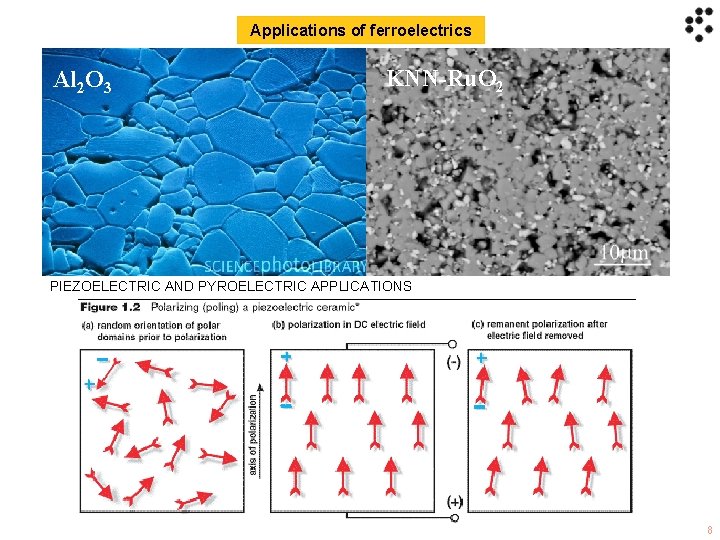
Applications of ferroelectrics Al O 2 3 CAPACITORS KNN-Ru. O 2 The nonlinear nature of ferroelectric materials can be used to make capacitors with tunable capacitance. Typically, a ferroelectric capacitor simply consists of a pair of electrodes sandwiching a layer of ferroelectric material. The permittivity of ferroelectrics is not only tunable but commonly also very high in absolute value, especially when close to the phase transition temperature. Because of this, ferroelectric capacitors are small in physical size compared to dielectric (non-tunable) capacitors of similar capacitance. MEMORY ELEMENTS The spontaneous polarization of ferroelectric materials implies a hysteresis effect which can be used as a memory function, and ferroelectric capacitors are indeed used to make ferroelectric RAM for computers. In these applications thin films of ferroelectric materials are typically used, as this allows the field required to switch the polarization to be achieved with a moderate voltage. PIEZOELECTRIC AND PYROELECTRIC APPLICATIONS Ferroelectric materials are required by symmetry considerations to be also piezoelectric and pyroelectric. The combined properties of memory, piezoelectricity, and pyroelectricity make ferroelectric capacitors very useful, e. g. for sensor applications. Ferroelectric capacitors are used in medical ultrasound machines (the capacitors generate and then listen for the ultrasound ping used to image the internal organs of a body), high quality infrared cameras (the infrared image is projected onto a two dimensional array of ferroelectric capacitors capable of detecting temperature differences as small as millionths of a degree Celsius), fire sensors, sonars, vibration sensors, and even fuel injectors on diesel engines. MULTIFERROICS Yet another hot topic is multiferroics, where researchers are looking for ways to couple magnetic and ferroelectric ordering within a material or heterostructure. 8

Time varying electric field complex dielectric constant – Electric displacement field of a full capacitor: – If the electric field varies with time then – Electric displacement field in t >t : (t is the time needed for a specific dipole moment to return into initial Follows the changes in position when E is switched off) time varying electric field. Electric polarization: We define: Is shifted for a Follows the changes in Is shifted for a phase of /2. time varying electric field. /2. Complex dielectric constant: 9

Imaginary part of the complex dielectric constant Heat losses released in aheat time period a unit ofvolume: -Heat, ’’ represents losseson per unit - ’ defines the volume of a practical device: Higher ’ – smaller device. - In practice: absolute released heat is more important then losses per unit volume. - Usually tan = ’’/ ’ is used to represent dielectric losses. 10

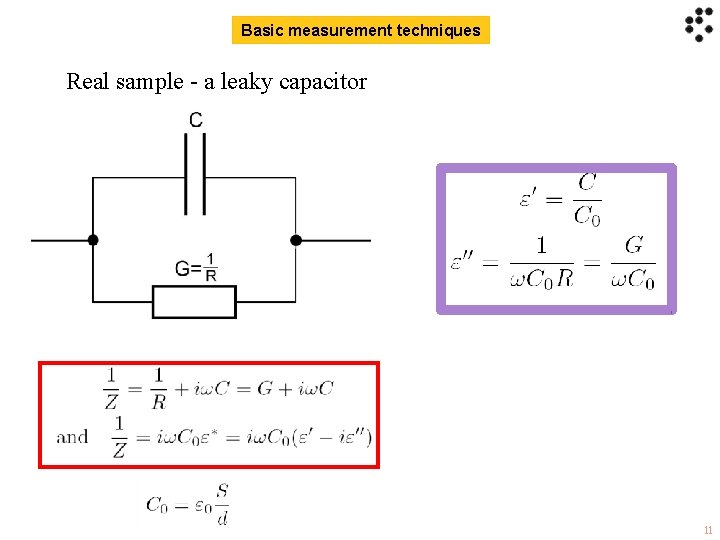
Basic measurement techniques Real sample - a leaky capacitor 11

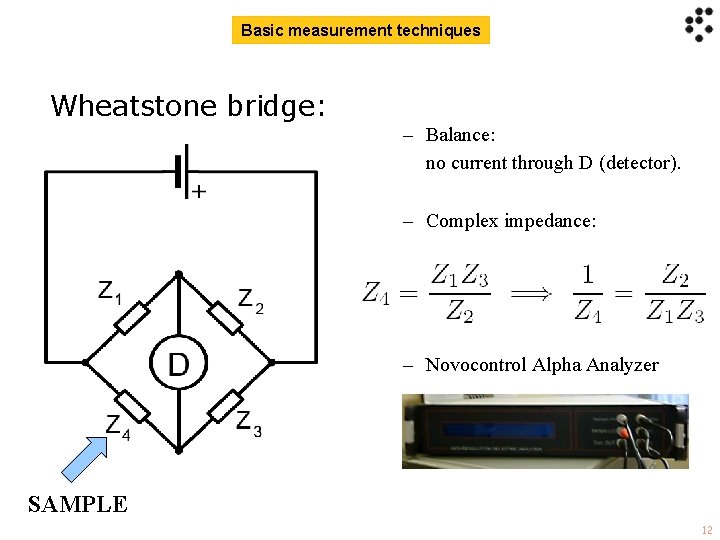
Basic measurement techniques Wheatstone bridge: – Balance: no current through D (detector). – Complex impedance: – Novocontrol Alpha Analyzer SAMPLE 12

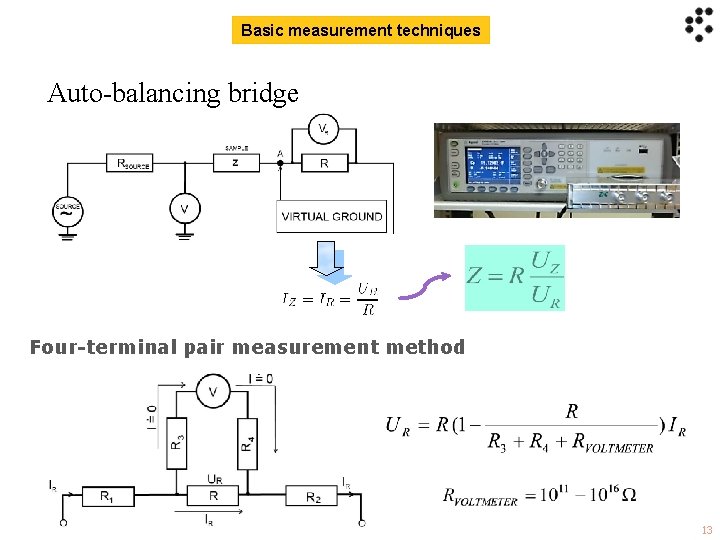
Basic measurement techniques Auto-balancing bridge Four-terminal pair measurement method 13

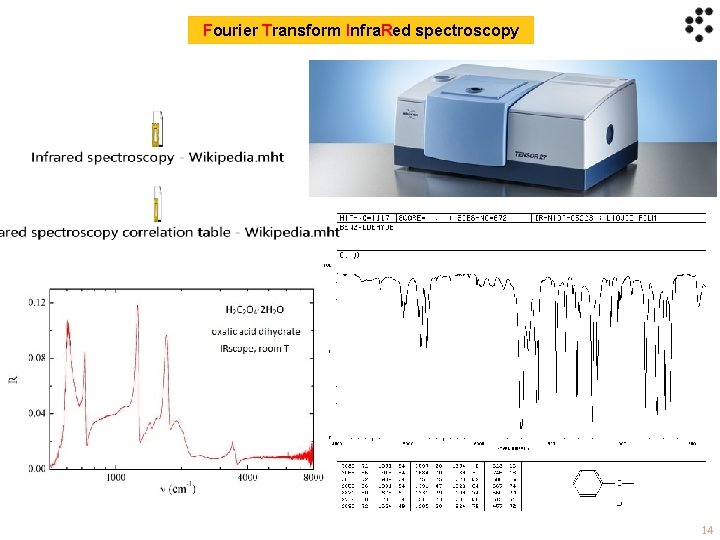
Fourier Transform Infra. Red spectroscopy 14