Fundamentals of Data Structures Vectors Computer Science Representing

Fundamentals of Data Structures Vectors Computer Science

Representing Vectors • Vectors are data structures that collect objects – Which can be added together – And multiplied by numbers (called scalars) • These objects (knowns as components of the vector) can be integers, real numbers, and other numerical types • Scalars are real/integer numbers 2 Fundamentals of Data Structures: Vectors

Representing Vectors • 3 Fundamentals of Data Structures: Vectors

Representing Vectors • 4 Fundamentals of Data Structures: Vectors

Representing Vectors • Every vector has a dimension – The number of components in a vector • If two (or more) vectors have the same dimension, we can perform some operations on them – Adding them together – Calculating the dot product of them • If we have a single vector and a scalar, we can multiply that vector by the scalar 5 Fundamentals of Data Structures: Vectors

Vector Operations • 6 Fundamentals of Data Structures: Vectors

• 7 Fundamentals of Data Structures: Vectors

Vector Operations • 8 Fundamentals of Data Structures: Vectors

• 9 Fundamentals of Data Structures: Vectors

Uses of Vectors • Although vectors can represent any collection of objects (i. e. numbers) • We do tend to use vectors for specific purposes – Especially in a computer program • Two of the most common uses of a vector are – Using a vector as a location in space – And using a vector as a direction 10 Fundamentals of Data Structures: Vectors

Uses of Vectors: Location • Any time we have space (no matter the number of dimensions), we usually have to represent points in space • For example, imagine we’re creating a 2 D game • We have the character and an enemy • They are in the following positions 11 Fundamentals of Data Structures: Vectors

Uses of Vectors: Location • 12 Fundamentals of Data Structures: Vectors

Uses of Vectors: Direction • We can also use vectors to represent a direction and strength of something – For example, the movement of the Character • These types of vectors are always represented by an arrow • Here the Character and Enemy have directions (their movement) 13 Fundamentals of Data Structures: Vectors

Uses of Vectors: Direction • 14 Fundamentals of Data Structures: Vectors

Uses of Vectors: Direction • 15 Fundamentals of Data Structures: Vectors

Uses of Vectors: Direction • 16 Fundamentals of Data Structures: Vectors

• Calculate the magnitude of the following vectors (to two decimal places) 17 Fundamentals of Data Structures: Vectors

Uses of Vectors • If you add to a position, you move the entity somewhere else in space – Scaling just affects the position further • If you add to a direction, you change the direction the entity is moving in – Scaling will increase or decrease the amount of movement in the same direction 18 Fundamentals of Data Structures: Vectors

Convex Combinations • 19 Fundamentals of Data Structures: Vectors

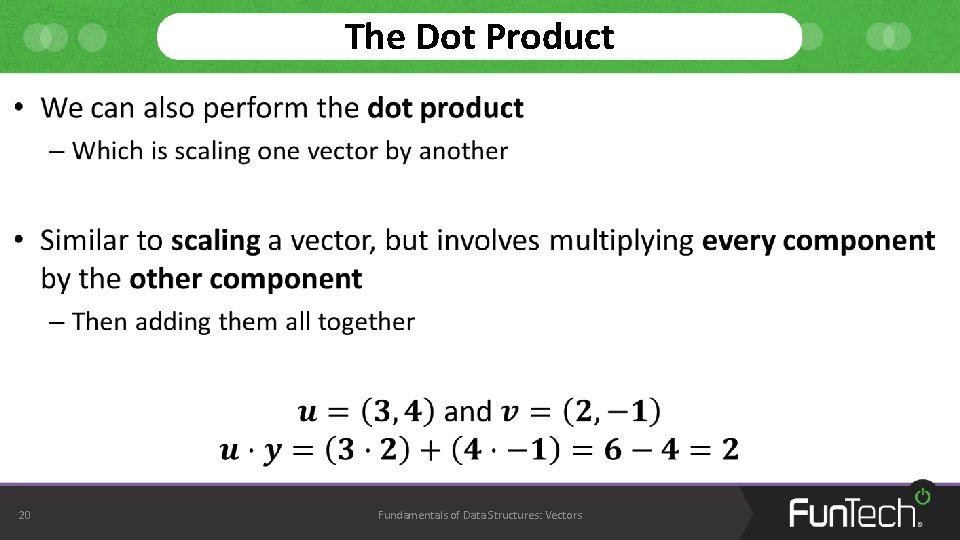
The Dot Product • 20 Fundamentals of Data Structures: Vectors

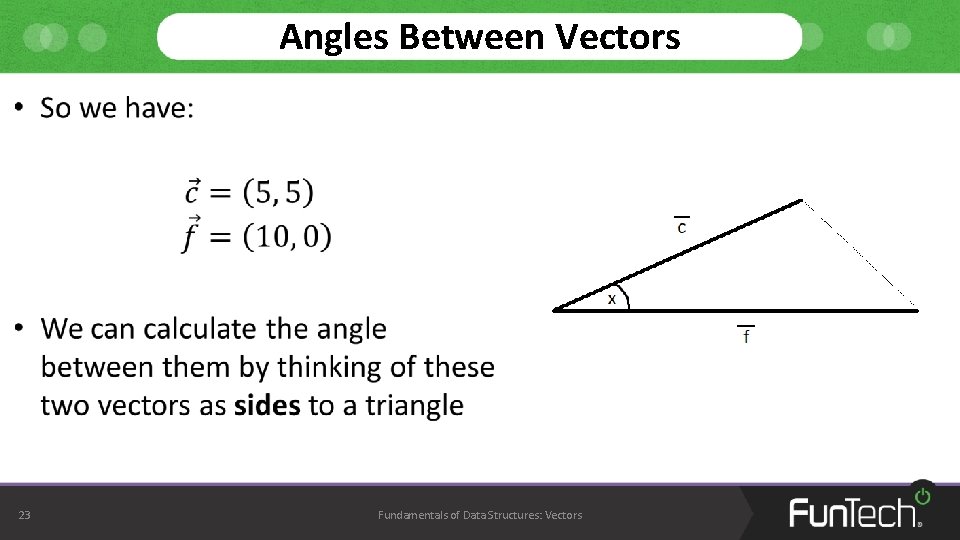
Angles Between Vectors • Another application of vector mathematics is calculating the angle between two directional vectors • Let’s say we have a character in a video game – And is facing one direction at the moment • We want them to face a different direction – So we know the direction they’re currently facing, and the direction to face • We need to calculate the angle to rotate the character by to face this new direction 21 Fundamentals of Data Structures: Vectors

Angles Between Vectors • 22 Fundamentals of Data Structures: Vectors

Angles Between Vectors • 23 Fundamentals of Data Structures: Vectors

Angles Between Vectors • 24 Fundamentals of Data Structures: Vectors

Angles Between Vectors • 25 Fundamentals of Data Structures: Vectors

• 26 Fundamentals of Data Structures: Vectors