Fundamentals of Computer Systems Boolean Logic Truth Tables

Fundamentals of Computer Systems Boolean Logic & Truth Tables Computer Science

Logic Gates • Computers (and us) use logic on a daily bases Do I want to eat something? Should I wear my coat? Meaning x y I am hungry True False I am not hungry False True • Logic is something that computers are great at • We boil logic down to two possible results: true and false Just like binary Meaning I am hungry • Computers use this logic via logic gates I am not hungry x 1 0

Circuit switches Electricity =0 Light =1 Statements = Conditions Light

Logic Gates: NOT • NOT acts as an inverse logic Anything that is true, is now false Anything that is false, is now true • For example: “I will go outside if it is not raining” • Here, raining is either true or false We only go outside if it is false • Also known as an inverter Input Output 0 1 1 0

Logic Gates: OR • OR combines two or more inputs into one output • The output is true if either of the inputs is true • Simply put, as long as one is true, the output is true Input A Input B Output 0 0 1 1 1 0 1 1

Logic Gates: AND • AND combines two or more inputs into one output • The output is true if both of the inputs is true • AND is more restrictive than OR Input A Input B Output 0 0 1 1 1

Logic Gates: XOR • XOR combines two or more inputs into one output • This is a more specific form of OR • The output is true only if one of the inputs is true The output is false if both the inputs are the same Input A Input B Output 0 0 1 1 1 0

Logic Gates: NOR and NAND • NOR and NAND are inverse the OR and AND gates • Simply reverse their usual output to get the new outputs Input A Input B Output 0 0 1 0 1 0 0 1 1 1 0 NOR NAND

Combining Logic • We create larger electrical components/systems by combining lots of logic gates • So we’ll usually see diagrams with lots of symbols • Questions may involve: Naming the logic gates Writing the algebraic expression (which we’ll see later) Completing/creating truth tables

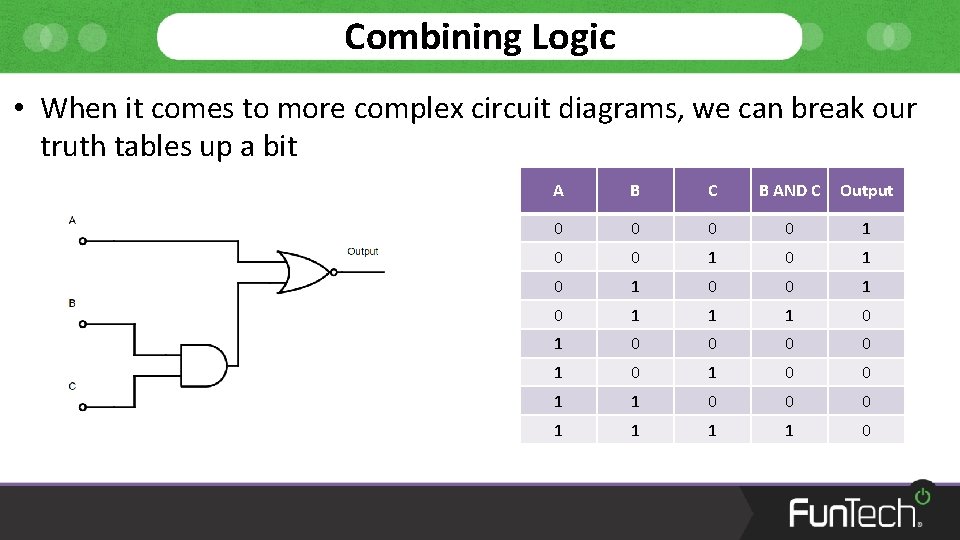
Combining Logic • When it comes to more complex circuit diagrams, we can break our truth tables up a bit A B C B AND C Output 0 0 1 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 1 1 0

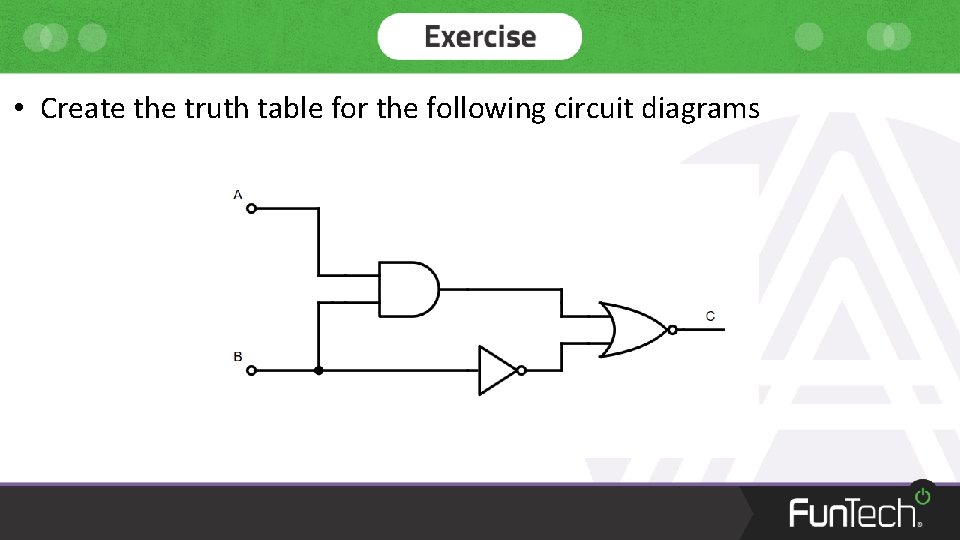
• Create the truth table for the following circuit diagrams

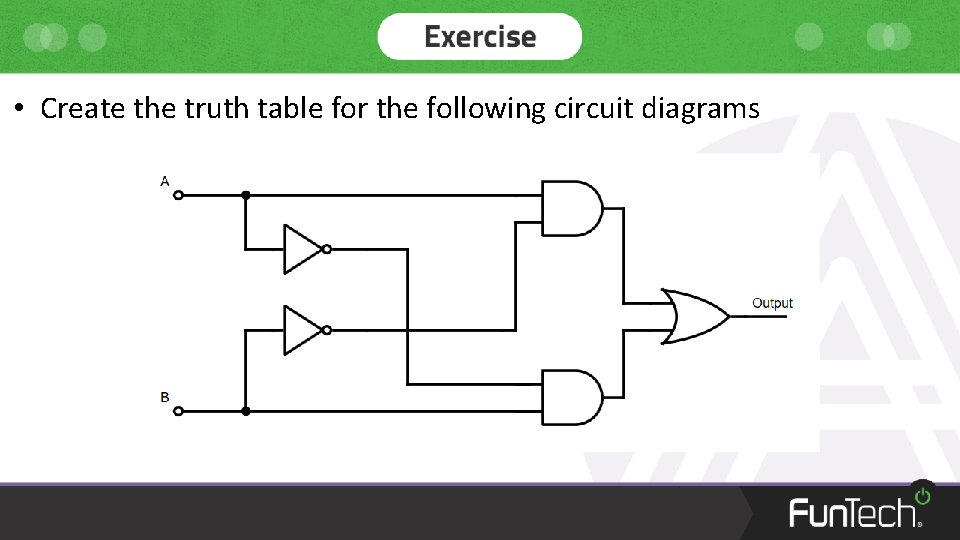
• Create the truth table for the following circuit diagrams

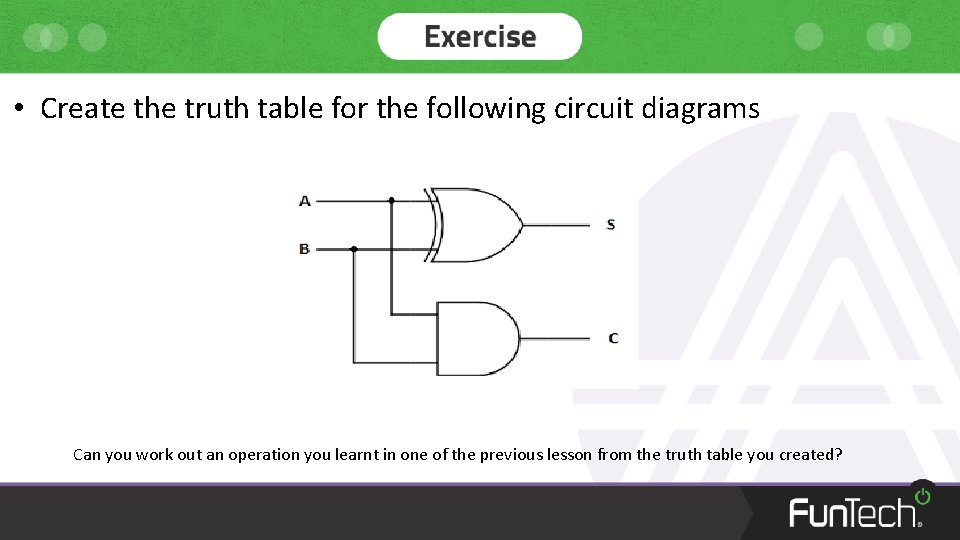
• Create the truth table for the following circuit diagrams Can you work out an operation you learnt in one of the previous lesson from the truth table you created?

Boolean Algebra • All logic gates can be represented using algebraic expressions • They use different notations to simplify logic circuit diagrams • Here, we use: Letters for the inputs Symbols for operations (like AND/OR)

Boolean Algebra: NOT • Uses a simple bar over the section being ‘notted’ (inverted) • Anything under the bar is inverted Can include letters and symbols

Boolean Algebra: OR • Uses the ‘+’ symbol to represent OR • Works a bit like statistics/probability in mathematics We ‘add’ probabilities together if it’s one or the other

Boolean Algebra: AND • Uses the ‘. ’ symbol to represent AND Represents ‘multiplication’ • Works a bit like statistics/probability in mathematics We ‘multiply’ probabilities together if it’s one and the other

Boolean Algebra: NOR and NAND • We simply add a bar over whole expressions (where needed) • Thus more complicated circuits can be written as a single expression

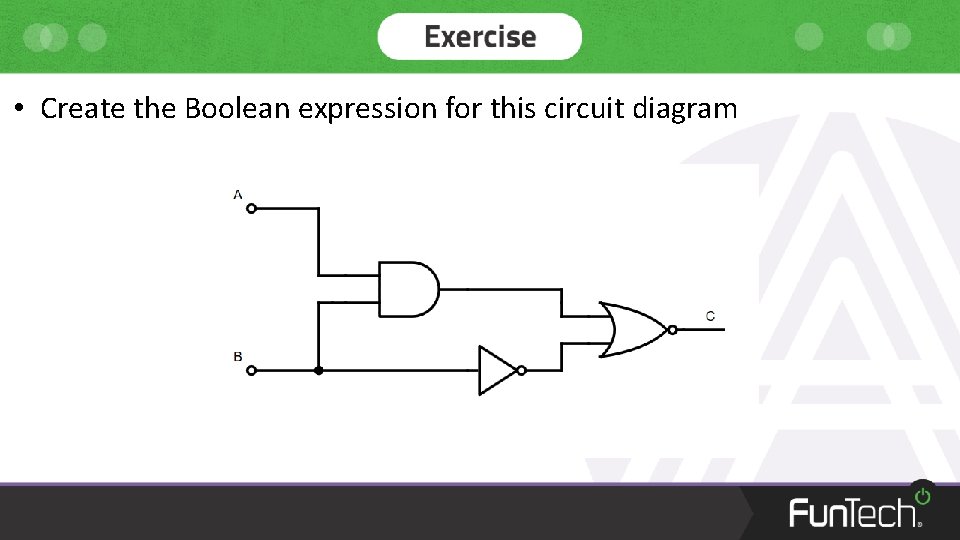
• Create the Boolean expression for this circuit diagram

• For the following boolean expressions, draw the circuit diagram and create a truth table

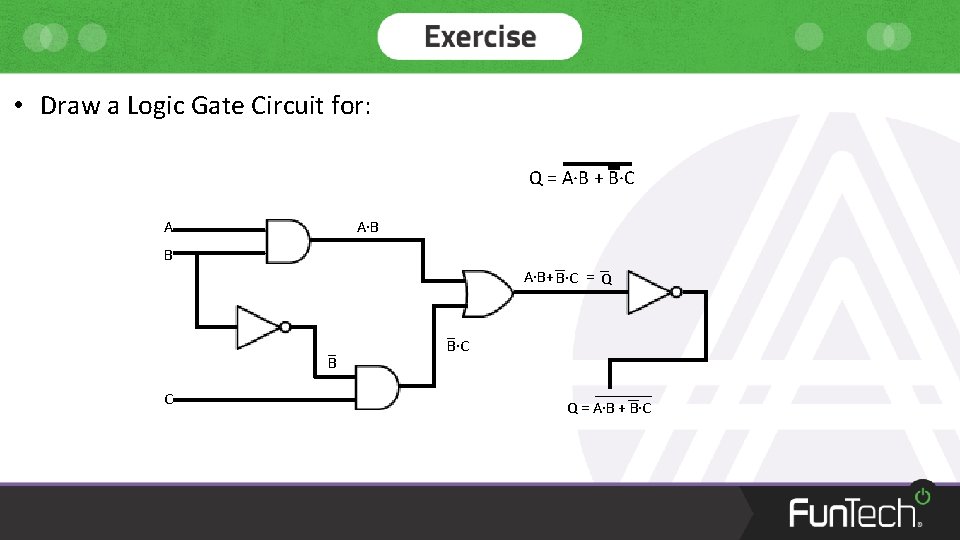
• Draw a Logic Gate Circuit for: Q = A·B + B·C A A·B B A·B+ B·C = Q B C B·C Q = A·B + B·C

Algebraic Laws • Commutative – Order of input not important • Associative – Order that sum is calculated not important • Distributive – Conjunction can always be rewritten as disjunction of two other conjunctions A+B = B+A A. B = B. A (A+B)+C = A+(B+C) (A. B). C = A. (B. C) A. (B + C) = (A. B) + (A. C)

Algebraic Laws • Identity – Boolean Algebra = Only 2 possible outcomes – 2 True outcomes = True A+0 = A A+1 = 1 A+A = A A+A = 1 A. 0 = 0 A. 1 = A A. A = 0 A + AB = A(1+(1. B)) = A. (1+B) = A. 1 = A A. (A+B) = A. A + A. B = A. (1+B) = A. 1 = A

De Morgan’s Laws • De Morgan’s Laws – Simplified Logic – Simplified Circuits NOR A+B NAND A. B • Modern processor chips – Millions of logic gates – All circuits can be reduced to combinations of one type

De Morgan’s Law • English Mathematician – Father, a Colonel in East India Company – Moved to England from India in the 19 th Century – Has a Moon crater named after him • Developed theories – Trigonometry – Algebra – De Morgan’s Laws

De Morgan’s Law • Simplifying Boolean algebra • Laws of Negatives • Create any logic gate circuit, using either: – OR & NOT – AND & NOT NOR A+B NAND A. B

De Morgan’s Law The negation of a conjunction is the disjunction of the negations A·B=A+B Substitution Form: A·B=A+B

De Morgan’s Law The negation of a disjunction is the conjunction of the negations A+B=A·B Substitution Form: A+B=A·B

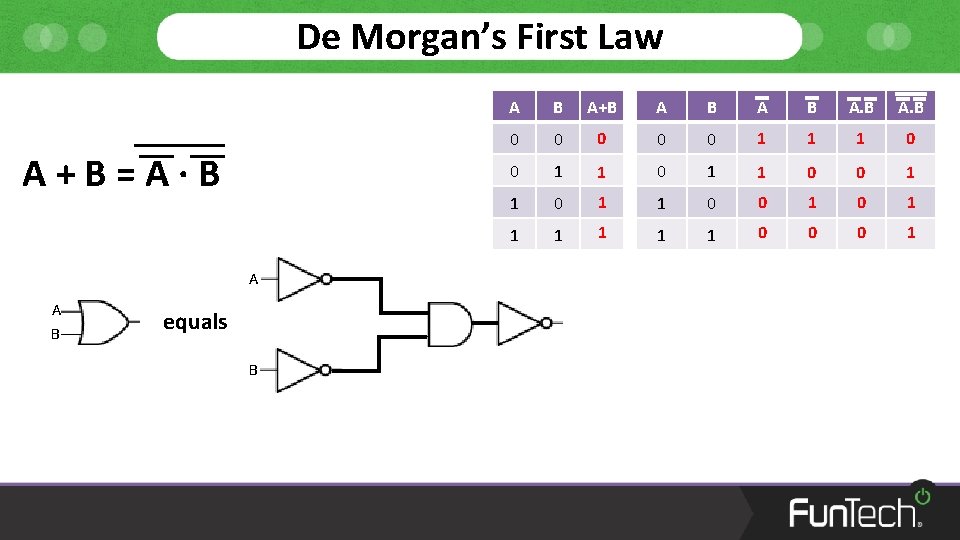
De Morgan’s First Law A+B=A·B A A B equals B A+B A B A. B 0 0 0 1 1 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1

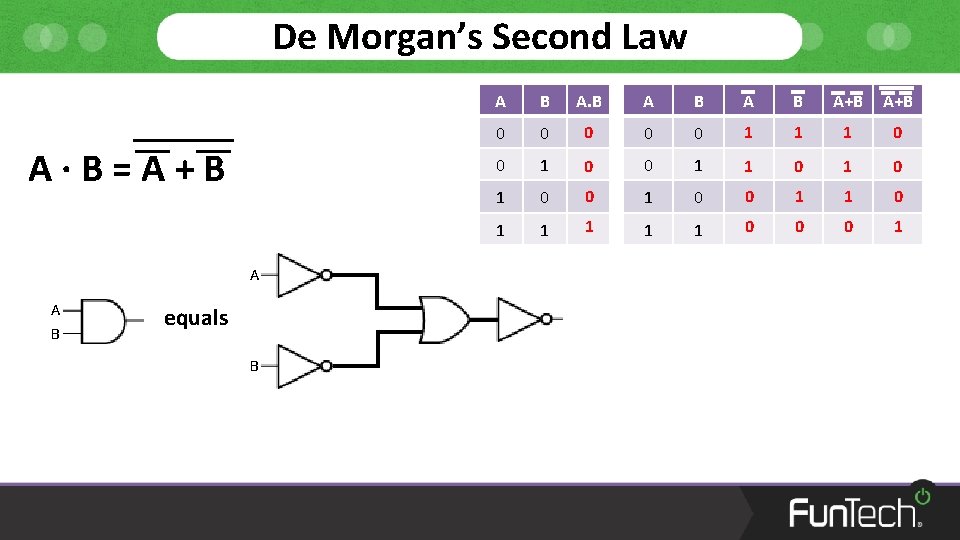
De Morgan’s Second Law A·B=A+B A A B equals B A B A+B 0 0 0 1 1 1 0 0 1 1 0 1 1 1 0 0 0 1

Memorising De Morgan’s Laws • De Morgan’s Laws may be written – Swap logical connection between the variables – Change logical state of each variable – Change logical state of the whole expression A. B A+B A. B

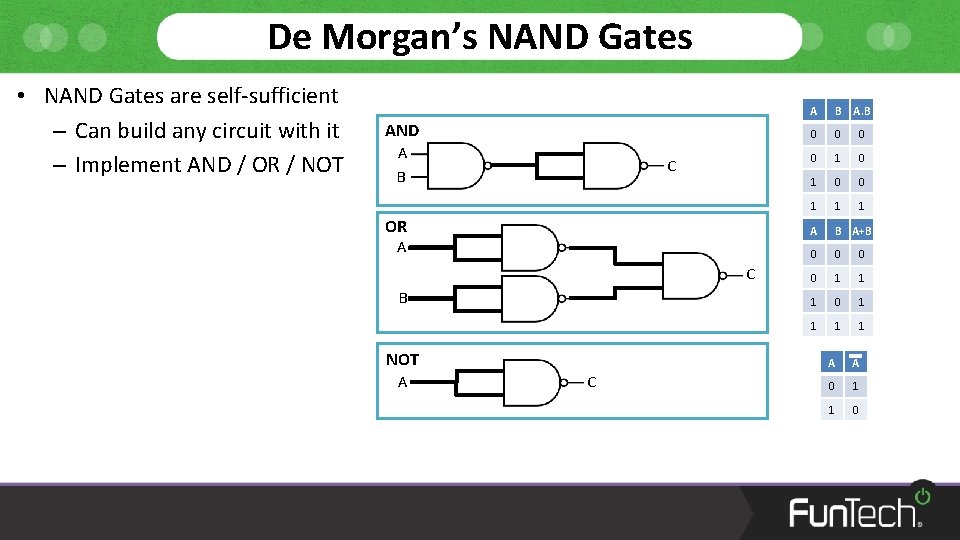
De Morgan’s NAND Gates • NAND Gates are self-sufficient – Can build any circuit with it – Implement AND / OR / NOT AND A B C OR A C B NOT A C A B A. B 0 0 1 1 1 A B A+B 0 0 1 1 1 0 1 1 A A 0 1 1 0

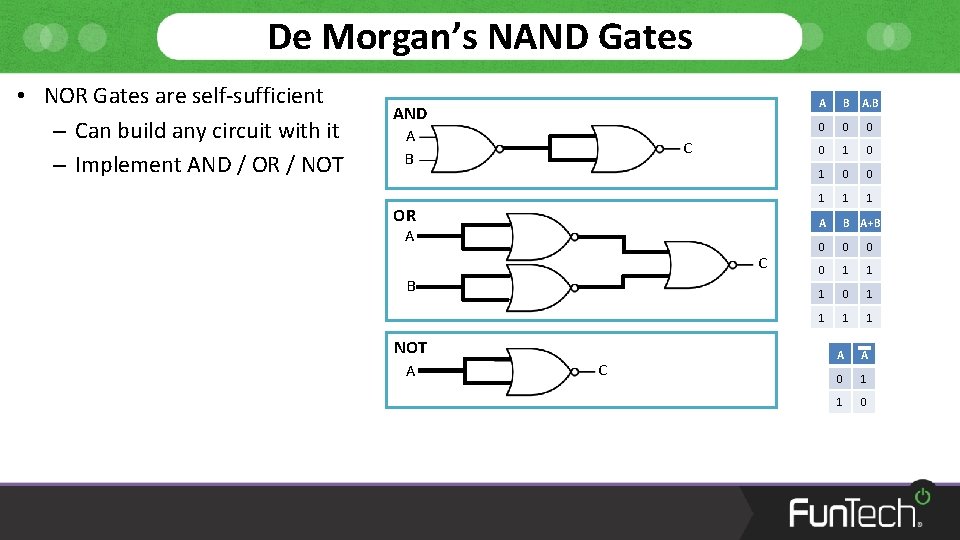
De Morgan’s NAND Gates • NOR Gates are self-sufficient – Can build any circuit with it – Implement AND / OR / NOT AND A B C OR A C B NOT A C A B A. B 0 0 1 1 1 A B A+B 0 0 1 1 1 0 1 1 A A 0 1 1 0

Simplification • Practice Boolean equation simplification: – – – – X. X. X Y+Y+Y X. Y + X. Y B. (A + A. B) X. Y + X X. (X+Y) !A. B + !A. !B • ! Denotes NOT – !(A + B). !B