Fundamentals of Computer Graphics Part 9 Discrete Techniques

Fundamentals of Computer Graphics Part 9 Discrete Techniques prof. ing. Václav Skala, CSc. University of West Bohemia Plzeň, Czech Republic © 2002 Prepared with Angel, E. : Interactive Computer Graphics – A Top Down Approach with Open. GL, Addison Wesley, 2001 Fundamentals of Computer Graphics

Discrete techniques Polygons, lines and others primitives transformed, rasterized and displayed API enables major mapping • texture mapping uses pattern to be put on a surface of an object • bump mapping – smooth surface is distorted to get variation of the surface • environmental mapping (reflection maps) – enables ray-tracing like output Fundamentals of Computer Graphics 2

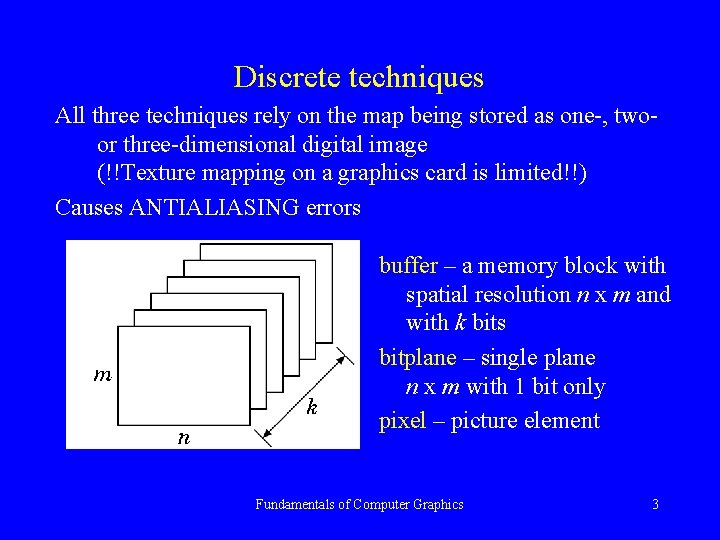
Discrete techniques All three techniques rely on the map being stored as one-, twoor three-dimensional digital image (!!Texture mapping on a graphics card is limited!!) Causes ANTIALIASING errors buffer – a memory block with spatial resolution n x m and with k bits bitplane – single plane n x m with 1 bit only pixel – picture element Fundamentals of Computer Graphics 3

Texture Mapping Regular patterns are mapped to an object’s surface Two dimensional texture T(s, t) s, t – texture coordinates stored in texture memory as n x m array of texture elements - texels Texture map associate a unique point of T with each point on a geometric object – mapped to screen coordinates Fundamentals of Computer Graphics 4

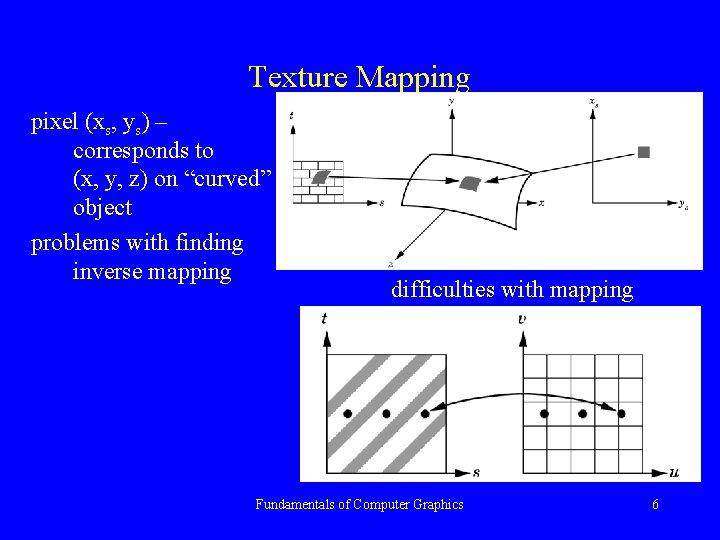
Texture Mapping Difficulties: - mapping from texture to geometric coordinates - 2 D texture defined over a rectangular region in the texture space -> mapping to 3 D region can be quite complex - rendering based on pixel-to-pixel approach – the inverse mapping from screen coordinates to texture coordinates is needed - because of shading – mapping areas-to-areas and not point-topoint is required -> antialising problems, moire patterns etc. Fundamentals of Computer Graphics 5

Texture Mapping pixel (xs, ys) – corresponds to (x, y, z) on “curved” object problems with finding inverse mapping difficulties with mapping Fundamentals of Computer Graphics 6

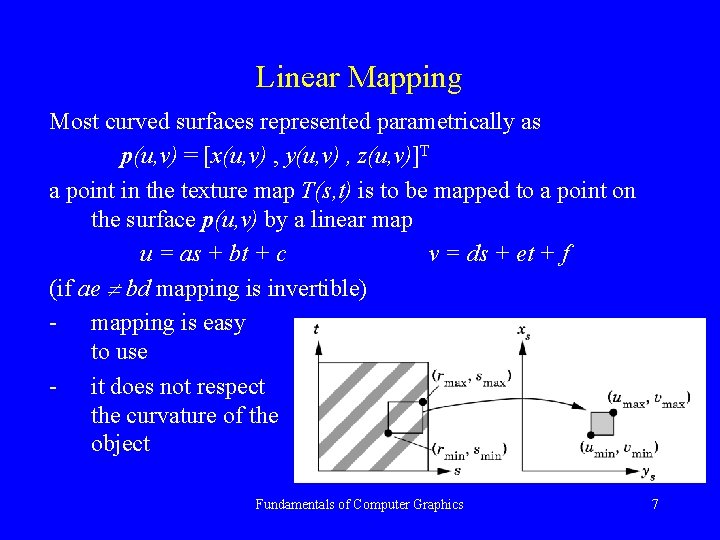
Linear Mapping Most curved surfaces represented parametrically as p(u, v) = [x(u, v) , y(u, v) , z(u, v)]T a point in the texture map T(s, t) is to be mapped to a point on the surface p(u, v) by a linear map u = as + bt + c v = ds + et + f (if ae bd mapping is invertible) - mapping is easy to use - it does not respect the curvature of the object Fundamentals of Computer Graphics 7

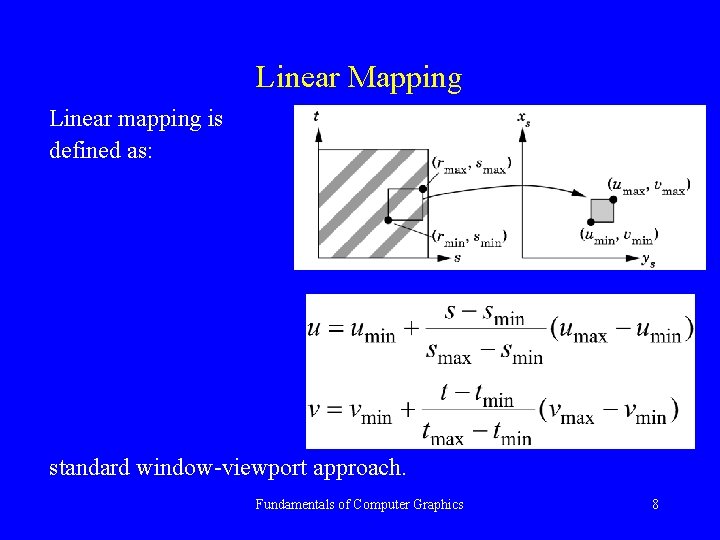
Linear Mapping Linear mapping is defined as: standard window-viewport approach. Fundamentals of Computer Graphics 8

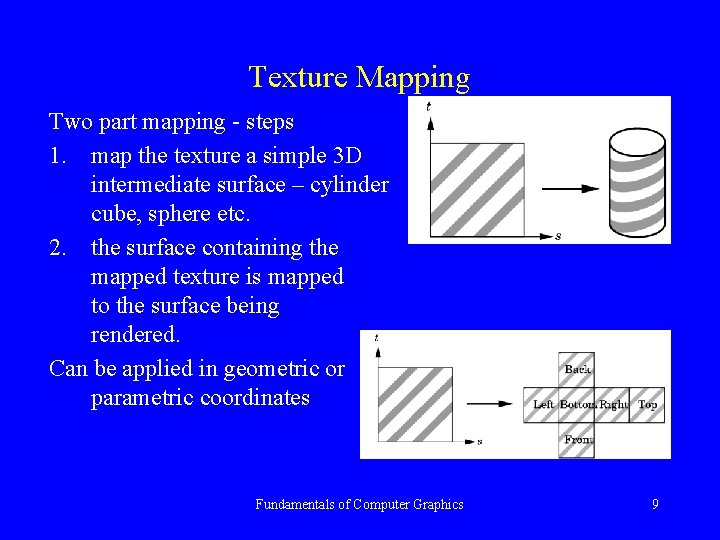
Texture Mapping Two part mapping - steps 1. map the texture a simple 3 D intermediate surface – cylinder cube, sphere etc. 2. the surface containing the mapped texture is mapped to the surface being rendered. Can be applied in geometric or parametric coordinates Fundamentals of Computer Graphics 9

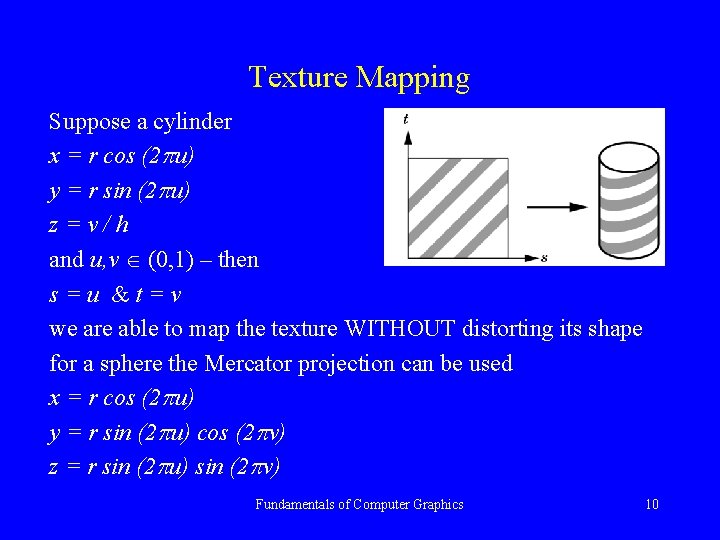
Texture Mapping Suppose a cylinder x = r cos (2 u) y = r sin (2 u) z=v/h and u, v (0, 1) – then s=u &t=v we are able to map the texture WITHOUT distorting its shape for a sphere the Mercator projection can be used x = r cos (2 u) y = r sin (2 u) cos (2 v) z = r sin (2 u) sin (2 v) Fundamentals of Computer Graphics 10

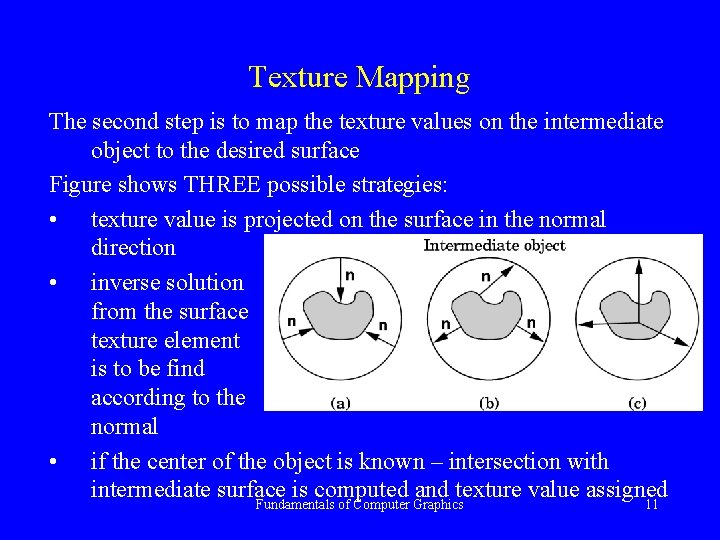
Texture Mapping The second step is to map the texture values on the intermediate object to the desired surface Figure shows THREE possible strategies: • texture value is projected on the surface in the normal direction • inverse solution from the surface texture element is to be find according to the normal • if the center of the object is known – intersection with intermediate surface is computed and texture value assigned Fundamentals of Computer Graphics 11

Texture Mapping in Open. GL – many mapping options including 1 D, 2 D & 3 D textures GLubyte my_texels [512]; /* generated somehow */ gl. Tex. Image 2 D(GL_TEXTURE, 0, 3, 512, 0, GL_RGB, GL_UNSIGNED_BYTE, my_texels); /* 0 & 3 – level & components, 0 – border, format – see latter*/ gl. Enable(GL_TEXTURE_2 D); /* enables texture mapping */ Fundamentals of Computer Graphics 12

Texture Mapping in Open. GL 2 D textures specification gl. Tex. Image 2 D(GL_TEXTURE, level, components, width, height, border, format, type, array); components (1 – 4 ) number of components RGBA to be affected with the map level & border – parameters for fine control Fundamentals of Computer Graphics 13

Texture Mapping in Open. GL gl. Begin(GL_QUAD); gl. Tex. Coord 2 f(0. 0, 0. 0); gl. Vertex 2 f(x 1, y 1, z 1); gl. Tex. Coord 2 f(1. 0, 0. 0); gl. Vertex 2 f(x 2, y 2, z 2); gl. Tex. Coord 2 f(0. 0, 1. 0); gl. Vertex 2 f(x 3, y 3, z 3); gl. Tex. Coord 2 f(1. 0, 1. 0); gl. Vertex 2 f(x 4, y 4, z 4); gl. End ( ); range of s, t changed to <0, 0. 5> Fundamentals of Computer Graphics 14

Texture Mapping in Open. GL STOP HERE!!! Fundamentals of Computer Graphics 15