Fundamentals of Chemistry How does chemistry relate to

Fundamentals of Chemistry How does chemistry relate to your world

What is Chemistry? � The study of the composition of matter and the changes that matter undergoes � Matter is anything that has mass and occupies space � Affects ALL aspects of life and most natural events

Fundamentals of Chemistry � Measurement ◦ Significance, Accuracy, Precision � Conversion ◦ Units, Matter, Energy � Balance ◦ Equilibrium, Mass, Energy � Change ◦ Physical and Chemical

Areas of Study � Organic – study of all chemicals containing Carbon � Inorganic – study of all chemicals not containing Carbon � Biochemistry – study of the processes that take place in organisms � Analytical – study that focuses on the composition of matter � Physical – study that deals with the mechanism, the rate, and the energy transfer that occurs when matter undergoes change

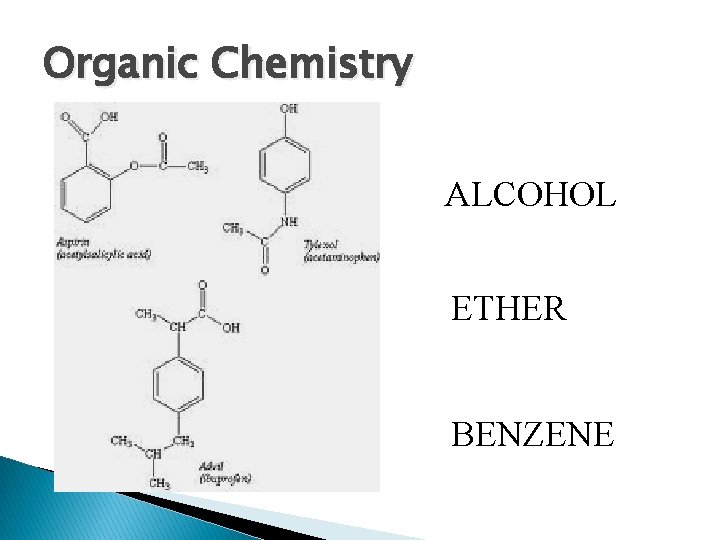
Organic Chemistry ALCOHOL ETHER BENZENE

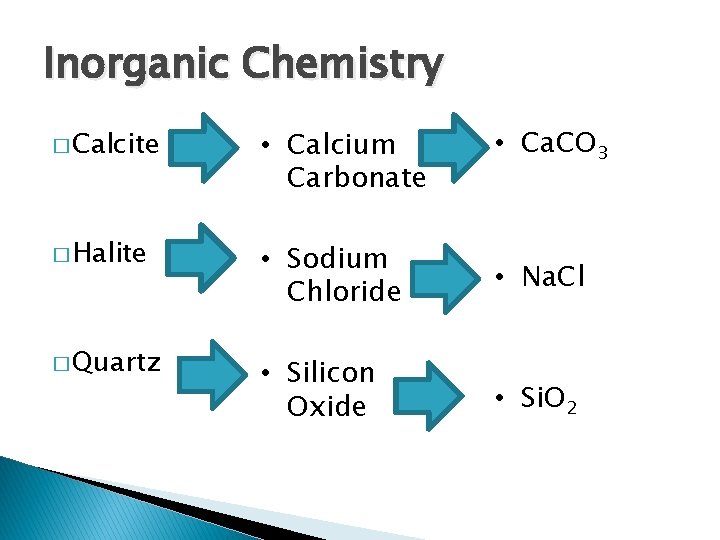
Inorganic Chemistry • Ca. CO 3 � Calcite • Calcium Carbonate � Halite • Sodium Chloride • Na. Cl • Silicon Oxide • Si. O 2 � Quartz

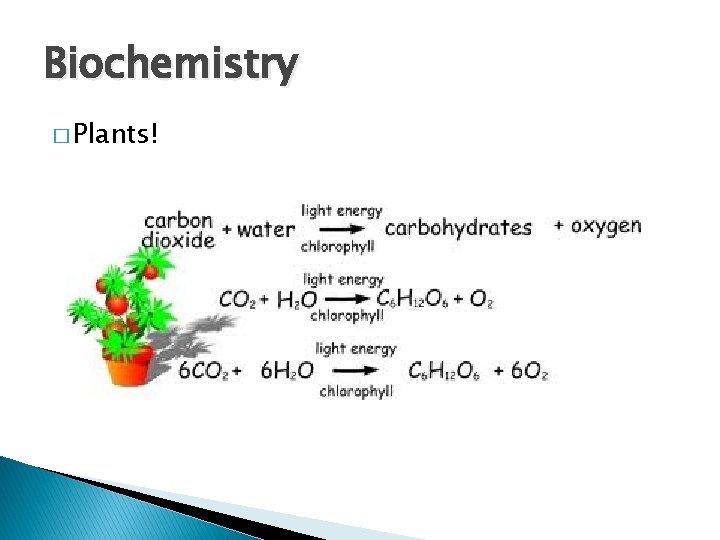
Biochemistry � Plants!

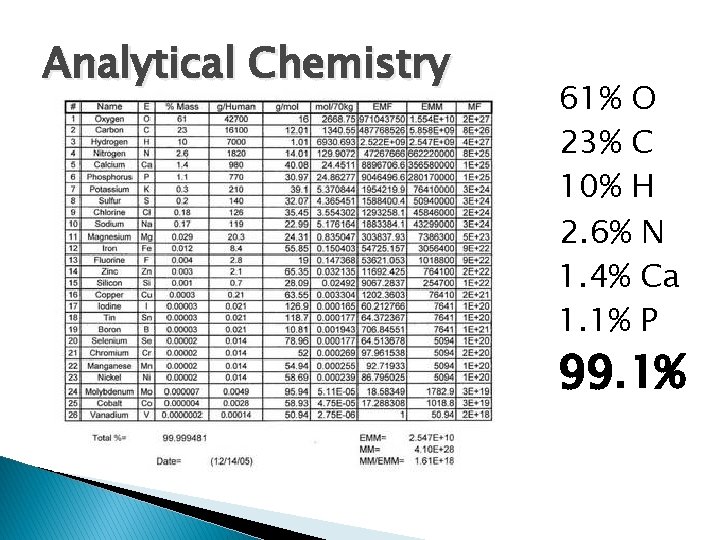
Analytical Chemistry 61% O 23% C 10% H 2. 6% N 1. 4% Ca 1. 1% P 99. 1%

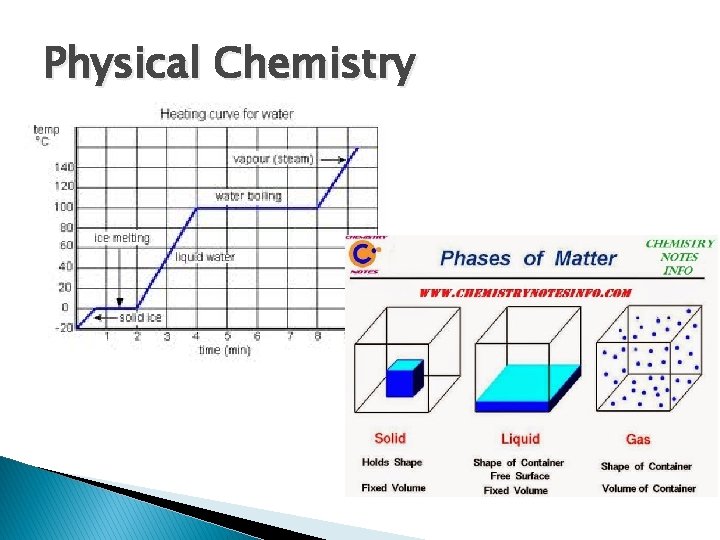
Physical Chemistry

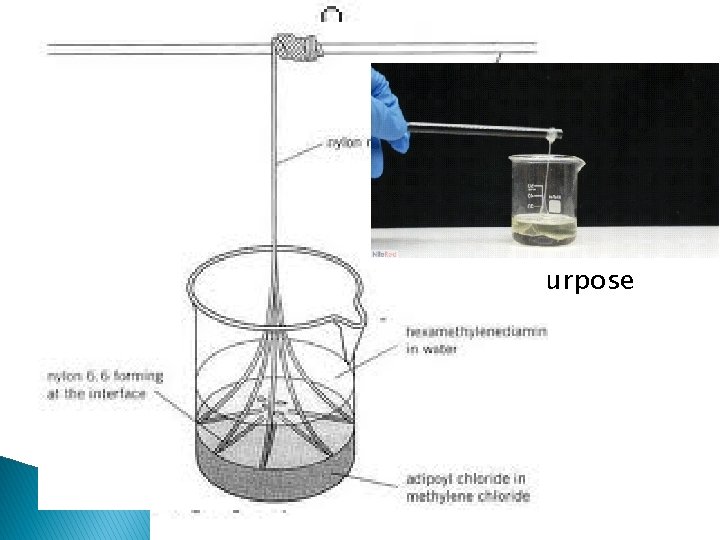
Pure v. Applied � Pure chemistry – research for research’s sake � Nylon � Applied � Aspirin chemistry – research for a purpose

The Scientific Method 1. 2. 3. 4. ◦ 5. 6. Purpose – Problem based on observations Research – Finding information for the problem Hypothesis – A potential solution Experiment – A series of tests challenging the solution Variables are identified (Independent, Dependent, Control, and Outlying) Data Collection – Results of experiments Analysis and Conclusion – Data based assessment of the proposed solution

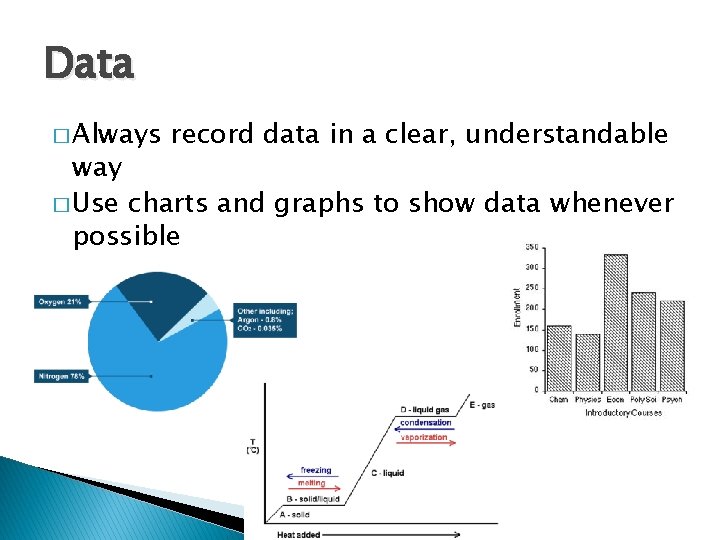
Data � Always record data in a clear, understandable way � Use charts and graphs to show data whenever possible

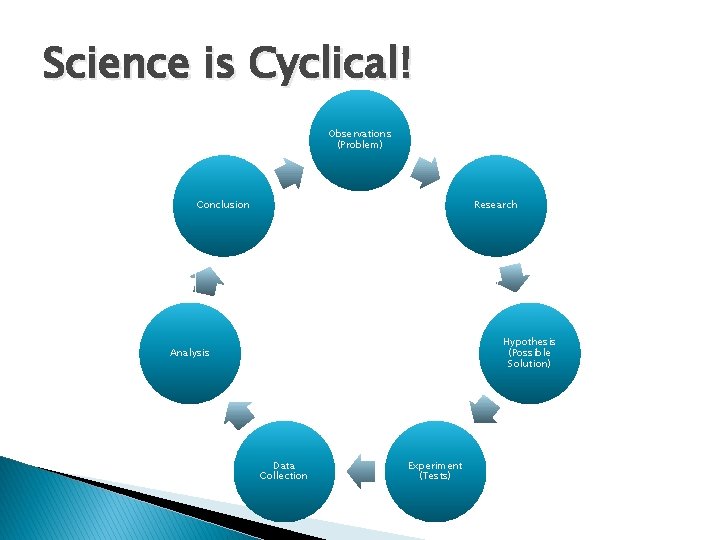
Science is Cyclical! Observations (Problem) Conclusion Research Hypothesis (Possible Solution) Analysis Data Collection Experiment (Tests)

Qualitative v. Quantitative � Qualitative = qualities, properties, or descriptions � Quantitative calculations � Give = numbers, measurements, or me two examples of each

Accuracy v. Precision � Accuracy – a measure of how close a measurement gets to the apparent or true value of whatever is measured � Precision – a measure of how close a series of measurements are to one another

Por Ejemplo

Ejemplo dos

Ejemplo tres

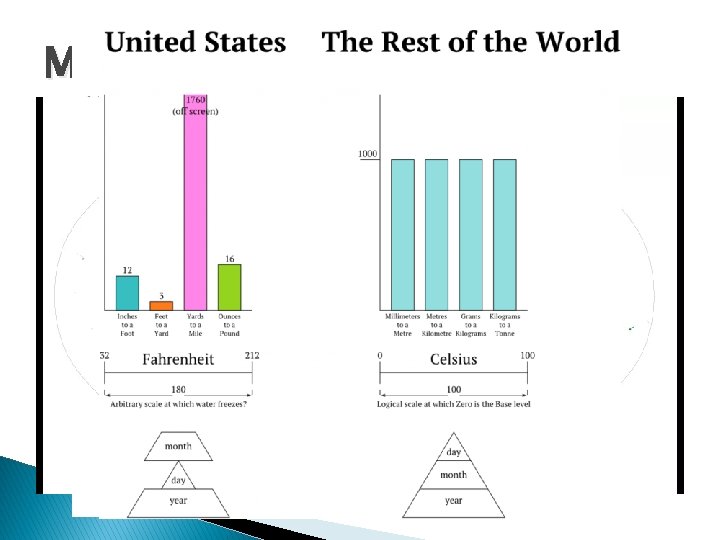
Metric vs. Imperial

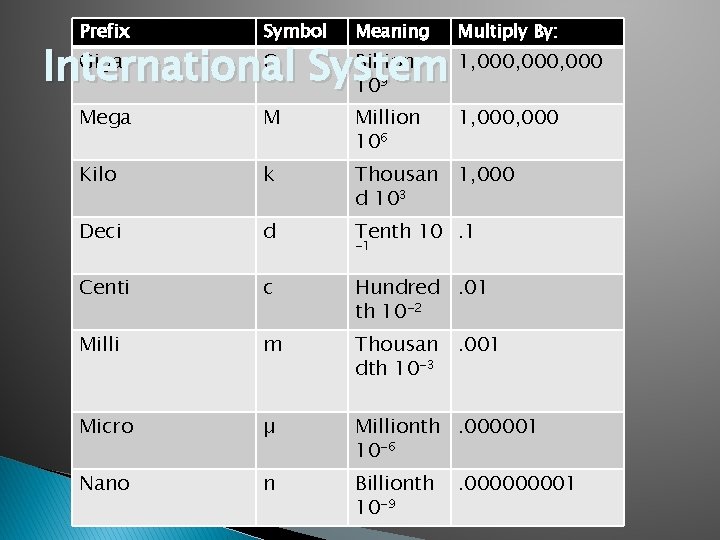
Prefix Symbol Meaning Multiply By: Giga G Billion 1, 000, 000 International System 10 9 Mega M Million 106 1, 000 Kilo k Thousan 1, 000 d 103 Deci d Tenth 10. 1 Centi c Hundred. 01 th 10 -2 Milli m Thousan. 001 dth 10 -3 Micro µ Millionth. 000001 10 -6 Nano n Billionth 10 -9 -1 . 00001

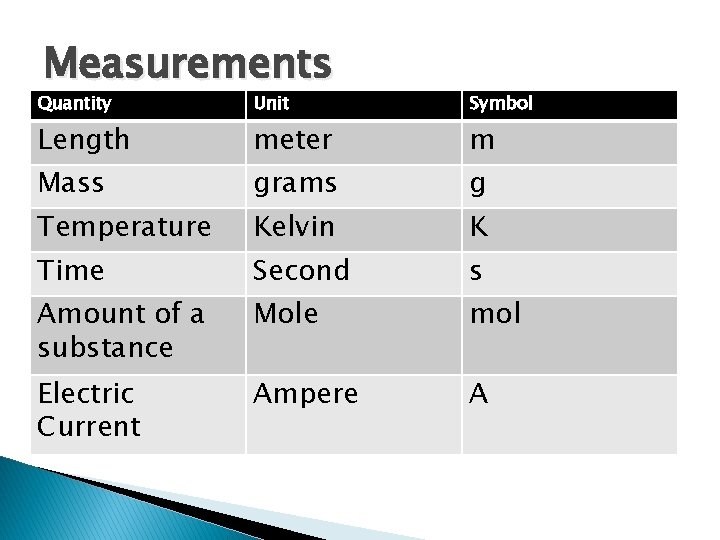
Measurements Quantity Unit Symbol Length meter m Mass grams g Temperature Kelvin K Time Second s Amount of a substance Mole mol Electric Current Ampere A

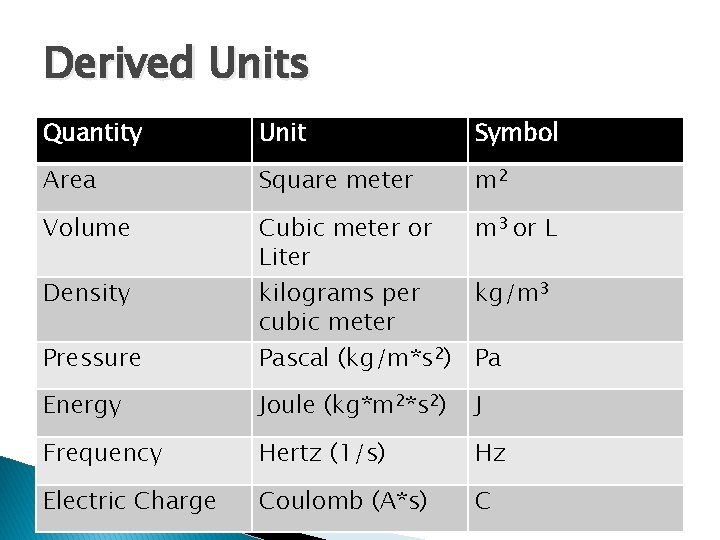
Derived Units Quantity Unit Symbol Area Square meter m 2 Volume Cubic meter or Liter m 3 or L Density kilograms per cubic meter kg/m 3 Energy Joule (kg*m 2*s 2) J Frequency Hertz (1/s) Hz Electric Charge Coulomb (A*s) C Pressure Pascal (kg/m*s 2) Pa

Practice � mm � mg � cm � km � Gg � Mm � ng � m. L � k. L • • • millimeters milligrams centimeters kilometers Gigagrams Megameters Nanograms Milliliters kiloliters

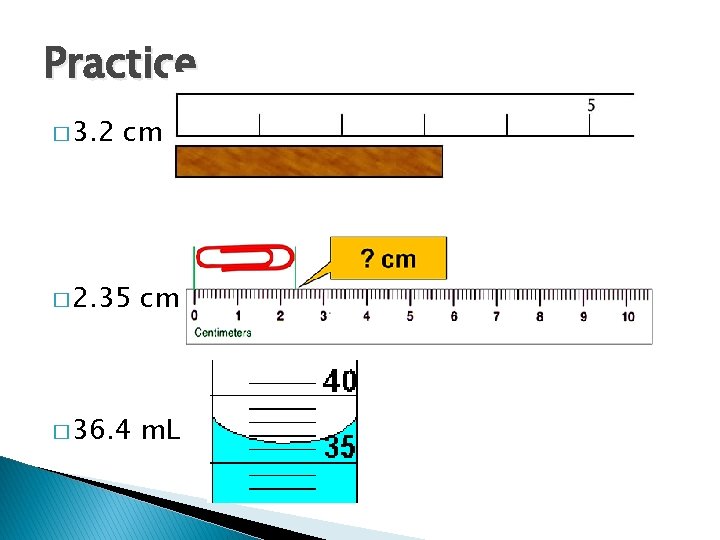
The Estimated Digit � In chemistry we will measure materials to an estimated digit � An estimated digit is a magnitude smaller than the tool we are measuring with � We can only go one magnitude because we want to be as accurate as possible

Practice � 3. 2 cm � 2. 35 cm � 36. 4 m. L

Scientific Notation � Written as the product of two numbers: a coefficient and 10 raised to a power � Therefore: 602, 000, 000, 000 � Equals: 6. 02 x 1023 � Or: 0. 00000775 � Equals: 7. 75 x 10 -10

Significant Figures � Includes all the digits that are known PLUS a last digit that is estimated when measuring � Calculations figures!!! � Significant are based on significant figures are based on a set of rules

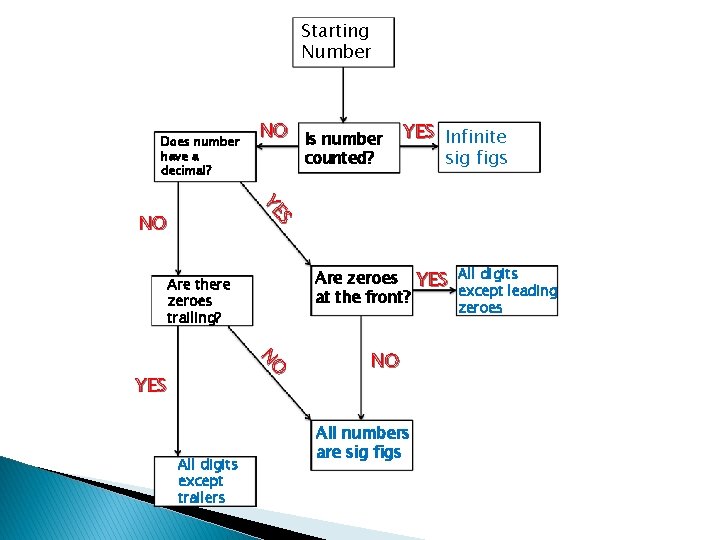
Significant Figure Rules 1. 2. 3. 4. Every nonzero digit in a reported measurement is assumed to be significant Zeros appearing between nonzero digits are significant Left most zeros appearing in front of nonzero digits are not significant Zeros at the end of a number and to the right of a decimal point are ALWAYS significant

Significant Figure Rules 5. Zeros at the right most end of a measurement that lie to the left of an understood decimal point are not significant if they serve as place holders to show the magnitude of the number, if zeros are at the right of a decimal point, they are significant 6. Exact quantities have an unlimited amount of significant figures

Starting Number Does number have a decimal? NO Is number counted? YES Infinite sig figs S YE NO Are zeroes YES All digits except leading at the front? Are there zeroes trailing? zeroes O N YES All digits except trailers NO All numbers are sig figs

Examples / Practice � 123 m � 9. 8000 x 104 m � 0. 07080 m � 40506 mm � 22 meter sticks � 98000 m � 3 (Rule 1) � 5 (Rule 4) � 4 (Rule 2, 3, 4) � 5 (Rule 2) � Unlimited (Rule 6) � 2 (Rule 5)

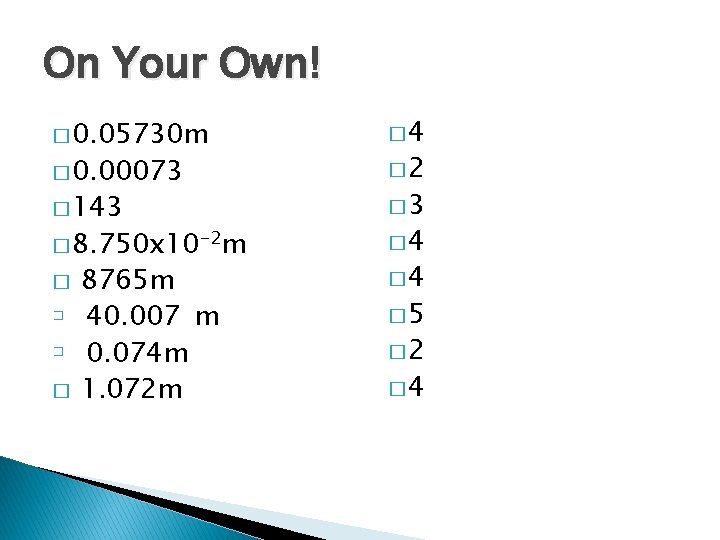
On Your Own! � 0. 05730 m � 4 � 143 � 0. 00073 � 8. 750 x 10 -2 m � � 8765 m 40. 007 m 0. 074 m 1. 072 m � 2 � 4 � 5 � 2 � 4

Adding and Subtracting � The answer to an addition or subtraction calculation should be rounded to the same number of decimal places (not including sig figs) as the measurement with the least number of decimal places � Ex. 12. 52 m + 349. 0 m + 8. 24 m = 369. 76 � Therefore: 369. 76 369. 8

Practice � 8. 3 m + 2. 22 m � 8432 m - 12. 5 m � 35. 2 sec + 2547 sec � 52 m – 0. 0042 m � 2. 4526 m + 8. 4 m � 2. 10 m - 0. 070 m � 1780 m + 0. 08 m � 53. 6 g - 0. 00056 g � 10. 5 m � 8420 m � 2582 sec � 52 m � 10. 9 m � 2. 03 m � 1780 m � 53. 6 g

Multiplying and Dividing � Round the answer to the same number of sig figs as the measurement with the least amount of sig figs � Ex. 7. 55 m x 0. 34 m = 2. 567 m 2 � Therefore: 2. 567 m 2 2. 6 m 2

Practice � 8. 3 m x 2. 22 m � 8432 m / 12. 5 � 35. 2 sec x 2547 � 0. 0042 m x 52 m � 2. 4526 m / 8. 4 � 2. 10 m x 0. 070 m � 1780 m / 0. 08 � 53. 6 g / 0. 00056 � 18 m 2 � 675 m � 89700 �. 22 m 2 sec �. 29 �. 15 m 2 � 20000 m or 2 x 104 m � 96000 m or 9. 6 x 104 m

Conversions � Units can be converted from one to another using a conversion factor or a simple equation � Chemistry using conversions for mass, volume, and parts

Conversion Factors 1 mole = molar mass = 6. 022 x 1023 = 22. 4 L of a gas 1 atm = 101. 3 k. Pa = 760 mm. Hg = 760 torr

Conversion Steps Starting Unit Conversion Factors

Conversion Practice 1. 2. 5 atm k. Pa 1. 250 k. Pa (253. 35) 2. 400 Cal J 2. 2 x 106 J (1. 672) 3. 75 °C °K 3. 348°K (350) 4. 356 g lbs 4. . 784 lbs.

What is Matter? � Anything that has a mass and takes up space � Matter has different classifications: ◦ ◦ ◦ ◦ Solid Liquid Gas Element Compound Homogeneous Heterogeneous � Matter is a cycle

What’s the difference? Solid – Crystalline structure, atoms are slow Liquid – Fixed volume but takes shape of container, atoms are faster Gas – Atoms are fastest, occupies any volume

What’s the difference? ELEMENT COMPOUND MOLECULE Elements – individual atoms Compounds – two different elements bonded together Molecule – two or more elements bonded together **Compounds are molecules, but molecules are not always compounds**

What is the difference? HETEROGENEOUS HOMOGENEOUS Homogeneous – Same throughout, cannot tell a difference, uniform Heterogeneous – Can see layers, mixture is not uniform

Changes in Matter � Physical change – effects shape, size, and appearance, but composition doesn’t change � Chemical change – effects shape, size, and appearance, but substance is chemically different How is color change both?

Changes in Properties

Changes in Matter - Reactions

End of Unit 1 To Be Continued…