Fundamentals of Chemical Kinetics Application to Combustible Systems

Fundamentals of Chemical Kinetics. Application to Combustible Systems and especially to the rate of formation and destruction of nitrogen oxides Gabrielle DUPRÉ Institute of Combustion, Aerodynamics, Reactivity and Environment (I. C. A. R. E. ), National Center of Scientific Research (C. N. R. S. ) and University of Orléans, ORLÉANS, France Università del Sannio, Benevento, Italy, May 30 -31, 2012 1

Fundamentals of chemical kinetics 1. Fundamentals of chemical kinetics 2. Elementary reactions 3. Characteristics of combustible mixtures 4. combustion processes 5. Formation of nitrogen oxides in combustion 2

1. Fundamentals of chemical kinetics 1. 0 - Introduction 1. 1 - Reaction rate 1. 2 - Reaction order, rate constant, activation energy, half-life time 1. 3 - Main types of reactions of a defined order 2. Elementary reactions 3. Characteristics of combustible mixtures 4. Reaction mechanisms in flames or in combustible processes 5. Formation of nitrogen oxides in combustion 3

11. Fundamentals of chemical kinetics 1. 0 - Introduction Study the rate of chemical reactions and of chemical mechanisms Aim: • Determine the time-evolution laws of chemical species (reactants, products, intermediate species) that takes part in a reaction • Interpret the time-dependent laws: An important factor: TIME Necessary condition: For a given reaction: Reactants Products • reaction must be thermodynamically possible: ΔAT, V ≤ 0 or ΔGT, P with A: utilizable energy (A = U – TS) ; G: free enthalpy (G = H – TS) ≤ 0 Non sufficient condition: Example: 2 H 2(g) + O 2(g) 2 H 2 O (l) • at T = 273 K, P = 101. 3 k. Pa: extremely slow reaction • at T > 873 K, for any P: explosive reaction Two important parameters: TEMPERATURE and PRESSURE 4

1. Fundamentals of chemical kinetics 1. 1 – Reaction rate 1. 1. 1 - General expression of the rate (v) of reaction: ν 1 A 1 + ν 2 A 2 +. . . ν 1’A’ 1 + ν 2’A’ 2 +. . . For species Ai: νi: stoichiometric coefficient ; [Ai]: species concentration [Ai] = ni /V with: ni: mole number ; V: reaction volume ; t: time νi dt i - = Reaction rate: v = - 1 d [Ai] = + 1 d [A’i] ν ’ dt 1 dni νi V dt + ni d. V νi V 2 dt if V is time-dependent 5

1. Fundamentals of chemical kinetics 1. 1 – Reaction rate 1. 1. 2 - Expression of reaction rate at constant V ν 1 A 1 + ν 2 A 2 +. . . ν 1’A’ 1 + ν 2’A’ 2 +. . . v= - 1 d [Ai] νi dt v = + 1’ d [A’i] ν i dt With constant reaction volume V: (v expressed in mol m-3 s-1) ni. d. V = 0 νi. V 2 dt 6

1. Fundamentals of chemical kinetics 1. 2 – Reaction order, rate constant, activation energy, half-life time 1. 2. 1 - Reaction order: m For the reaction: νAA + νBB Products v = k [A]m. A [B]m. B with (v expressed in mol m-3 s-1) k: rate constant ; m. A and m. B: partial orders m. A + m. B = m: overall order If: m. A = νA and m. B = νB ↔ ‘elementary reaction’ 7

1. Fundamentals of chemical kinetics 1. 2 – Reaction order, rate constant, activation energy, half-life time 1. 2. 2 – Rate constant: k For the reaction: νAA + νBB Products v = k [A]m. A [B]m. B with: k = k 0 exp (- Ea / RT) Arrhenius law v: reaction rate (mol m-3 s-1) k: rate constant ; k 0: pre-exponential factor ; k and k 0: same units as v Ea: activation energy (J mol-1) R: perfect gas constant (J mol-1 K-1) ; T: temperature (K) 8

1. Fundamentals of chemical kinetics 1. 2 – Reaction order, rate constant, activation energy, half-life time 1. 2. 3 – Activation energy: Ea For the reaction: k = k 0 exp (- Ea / RT) Determination of Ea from: - the linear representation: ln k = f (1 / T) k 0, Ea - the measurements of v or k at two different temperatures T 1 and T 2 if T 1 ≠ T 2 : v 1/v 2 = k 1/k 2 = (k 0)1/(k 0)2 exp[-Ea/R (1/T 1 – 1/T 2)] if T 1 # T 2 : (k 0)1 # (k 0)2 ; (k 0)1/(k 0)2 # 1 Ea 9

1. Fundamentals of chemical kinetics 1. 2 – Reaction order, rate constant, activation energy, half-life time 1. 2. 4 – Half-life time: t½ at at A + B Products a b a–x b–x t=0 t The half-life t½ is the time corresponding to the half of reactant initial concentration a or b: at t = t½ a–x = a/2 ↔ x=a/2 or b–x = b/2 ↔ x=b/2 10

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order 1. 3. 0 - Order 0: (m = 0) with a unique reactant (ν = 1): this case is rather rare ! A at at t=0 t a a–x Reaction rate: Concentration: Units for k: Half-life: Products 0 v=? [A] = f (t)? ? t½ = ? 11

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order 1. 3. 1 – Order 1: (m = 1) with a unique reactant (ν = 1): this case appears mostly for disintegration of radioactive atoms. A at at t=0 t a a–x Reaction rate: Concentration: Units for k: Half-life: Products 0 v=? [A] = f (t)? ? t½ = ? 12

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order 1. 3. 2 – Order 1: (m = 1) with 2 reactants (νA = νB = 1) with one reactant in excess A at at t=0 t If b >> a a a–x + B Products b b–x avec a > x Reaction rate: Concentration: Units for k: Half-life: 0 b >> x b–x # b v=? [A] = f (t)? ? t½ = ? 13

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order Most chemical reactions are bimolecular 1. 3. 3 – Order 2: (m = 2) with a unique reactant (νA = 1) A Products at at t=0 t a a–x Reaction rate: Concentration: Units for k: Half-life: 0 v=? [A] = f (t)? ? t½ = ? 14

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order 1. 3. 4 – Order 2: (m = 2) with 2 reactants (νA = νB = 1) at at t=0 t A + B a b a–x b–x Products 0 1) for a ≠ b Reaction rate: Concentration: Units for k: Half-life: v=? [A] = f (t)? ? t½ = ? 2) for a = b See the case of m = 2, ν = 1 for a unique reactant 15

1. Fundamentals of chemical kinetics 1. 3 – Main types of reactions of a defined order We could treat also reactions of order 3: these reactions do exist but are rare because of a low probability of three species colliding simultaneously 1. 3. 5 – Order 3: (m = 3) with a 1 reactant (νA = 1) 1. 3. 6 – Order 3: (m = 3) with a 2 reactants (νA = 2 ; νB = 1 for example) We could also treat reactions of any order m (whole or fractional) 1. 3. 7 – Order m: (m ≠ 1 or m = 1) with 1 reactant (ν = 1) 16

Fundamentals of chemical kinetics Application to combustible mixtures 1. Fundamentals of chemical kinetics 2. Elementary reactions 2. 1 – Bimolecular reactions at constant volume 2. 2 – Collision Theory of gas reactions 2. 3 – Activated-Complex Theory 3. Characteristics of combustible mixtures 4. Reaction mechanisms in flames 5. Formation of nitrogen oxides in combustion 17

2. Elementary reactions 2. 1 – Bimolecular reactions at constant volume A + B P (P = Products) with νA = m. A = 1 et νB = m. B = 1 (≡ elementary reaction of order 2) • v = - d[A]/dt = - d[B]/dt = + d[P]/dt • v = k [A]1 [B]1 • Generally: k = k 0 exp[-Ea/RT] 18

2. Elementary reactions 2. 2 – Collision Theory for gaseous reactions • Any chemical reaction results more likely of a collision between two chemical species, through an elementary act (except for the disintegration process of a radioactive atom: m=1 and for the collision - rare - between three species) • The collision frequency is evaluated on the basis of the kinetic theory of gases 19

2. Elementary reactions 2. 2 - Collision Theory for gaseous reactions • Any chemical reaction results of a collision between two chemical species through an elementary act • The collision frequency ZAB is evaluated on the basis of the kinetic theory of gases (assuming that the chemical species are like hard spheres): ZAB = σAB c. AB [NA/V ] [NB/V ] with: d. AB = ½ (d. A+d. B) σAB = π (d. AB)2 B A B [expressed in coll. m-3 s-1] B c. AB = (8 k. BT/π µAB)1/2 where 1/µAB = 1/m. A+1/m. B σAB c. AB NA/V = n. A NB/V = n. B B 20

2. 2 - Collision Theory for gaseous reactions ZAB = [NA/V ] [NB/V ] (8 k. BT/π µAB)1/2 π (d. AB)2 with NA/V = n. A and NB/V = n. B n. A, n. B: numbers of molecules A and B per volume unit ZAB = n. A n. B (8 k. BT/π µAB)1/2 π (d. AB)2 • Each collision is not a reactive process: v << ZAB • Two limiting factors : - Energetic factor: f = exp (-EA/RT) - Steric factor: p v = - dn. A/dt = ZAB p exp(-EA/RT) = k n. A n. B k = (8 k. BT/π µAB)1/2 π (d. AB)2 p exp(-EA/RT) = k 0 exp(-EA/RT) With: k 0 = (8 k. BT/π µAB)1/2 π (d. AB)2 p 21

2. Elementary reactions 2. 2 - Collision Theory for gaseous reactions Finally : - d[n. A]/dt = n. A n. B σAB c. AB p exp (-EA/RT) = k n. A n. B Rate constant : k = σAB c. AB p exp (-EA/RT) 22

2. Elementary reactions 2. 2 - Collision Theory for gaseous reactions Validity of the collision theory for gaseous reactions ? How to evaluate EA ? How to estimate p ? 23

2. Elementary reactions 2. 3 – Activated-Complex Theory Existence of a transition state and activated complex: (AB‡) A + B AB‡ P P = Products with K‡ : pseudo-equilibrium constant: K‡ = [AB‡] c°/ [A] [B] v = + d[P]/dt = ν‡ [AB‡] = ν‡ K‡ [A] [B] / c° v = k. II [A] [B] k. II : bimolecular rate constant where: ν‡ : vibration frequency of the bond in AB‡ that breaks to give products c° : concentration in the reference state (= P°/RT° for a gaseous reaction) = 1 mol m-3 (in the International Unit System) k. II = ν‡ K‡ / c° 24

2. Elementary reactions 2. 3 – Activated-Complex Theory Expression de K‡ ? ? 25

2. Elementary reactions 2. 3 – Activated-Complex Theory Calculation of K‡ from the partition functions of energy Qi K‡ = (QAB ‡ / QA QB) exp (- E‡ 0 /RT) with: Qi = (qe qn qtr 3 qrota qvib 3 N-b)i for each species i N: number of atoms in the species i a = 2 ; b = 5 for a linear molecule a = 3 ; b = 6 for a non-linear molecule E‡ 0: difference of potential energy between (AB‡) and reactants 26

2. Elementary reactions 2. 3 – Activated-Complex Theory K‡ = (QAB ‡ / QA QB) exp (- E‡ 0 /RT) If: h ν‡ << k. B T QAB‡ = Q’AB‡ / [1 – exp (- hν‡/k. BT)] # Q’AB‡ k. BT / hν‡ where Q’AB‡ is the product of all terms not dealing with bond scission ν‡ : vibration frequency of the bond in AB‡ that breaks to give products h : Planck constant ; k. B: Boltzmann constant ; T: temperature 27

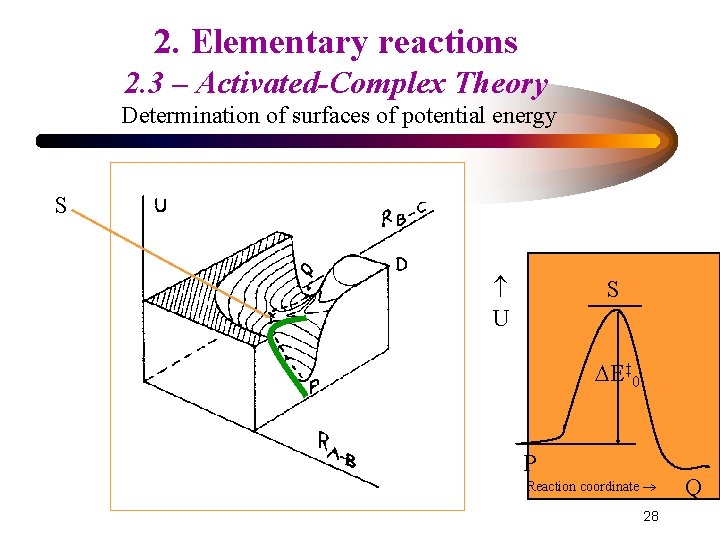
2. Elementary reactions 2. 3 – Activated-Complex Theory Determination of surfaces of potential energy S U S E‡ 0 P Reaction coordinate 28 Q

2. Elementary reactions 2. 3 – Activated-Complex Theory Calculation of K‡ from the partition functions of energy Qi Calculation of k. II: k. II = ν‡ K‡ / c° becomes: k. II = (Q’AB‡ / QA QB) (k. BT/h) (1/c°) exp(- E‡ 0 /RT) 29

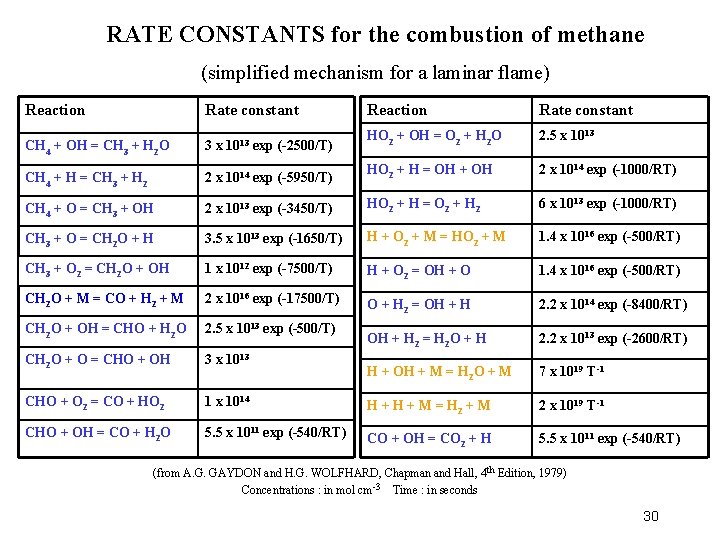
RATE CONSTANTS for the combustion of methane (simplified mechanism for a laminar flame) Reaction Rate constant CH 4 + OH = CH 3 + H 2 O 3 x 1013 exp (-2500/T) HO 2 + OH = O 2 + H 2 O 2. 5 x 1013 CH 4 + H = CH 3 + H 2 2 x 1014 exp (-5950/T) HO 2 + H = OH + OH 2 x 1014 exp (-1000/RT) CH 4 + O = CH 3 + OH 2 x 1013 exp (-3450/T) HO 2 + H = O 2 + H 2 6 x 1013 exp (-1000/RT) CH 3 + O = CH 2 O + H 3. 5 x 1013 exp (-1650/T) H + O 2 + M = HO 2 + M 1. 4 x 1016 exp (-500/RT) CH 3 + O 2 = CH 2 O + OH 1 x 1012 exp (-7500/T) H + O 2 = OH + O 1. 4 x 1016 exp (-500/RT) CH 2 O + M = CO + H 2 + M 2 x 1016 exp (-17500/T) O + H 2 = OH + H 2. 2 x 1014 exp (-8400/RT) CH 2 O + OH = CHO + H 2 O 2. 5 x 1013 exp (-500/T) OH + H 2 = H 2 O + H 2. 2 x 1013 exp (-2600/RT) CH 2 O + O = CHO + OH 3 x 1013 H + OH + M = H 2 O + M 7 x 1019 T-1 CHO + O 2 = CO + HO 2 1 x 1014 H + M = H 2 + M 2 x 1019 T-1 CHO + OH = CO + H 2 O 5. 5 x 1011 exp (-540/RT) CO + OH = CO 2 + H 5. 5 x 1011 exp (-540/RT) (from A. G. GAYDON and H. G. WOLFHARD, Chapman and Hall, 4 th Edition, 1979) Concentrations : in mol cm -3 Time : in seconds 30

2. Elementary reactions 2. 3 – Activated-Complex Theory • Difficulties encountered with ab initio methods: - Calculation of E‡ 0 – Determination of surfaces of potential energy - Calculation of partition functions of energy for the activated complex – Structure of activated complex • GAUSSIAN software: a good help for the selection of reaction steps 31

Fundamentals of chemical kinetics Application to combustible mixtures 1. Fundamentals of chemical kinetics 2. Elementary reactions 3. Characteristics of combustible mixtures 4. Reaction mechanisms in flames 5. Formation of nitrogen oxides in combustion 32

3. Characteristics of combustible mixtures • The chemical reaction occurs in gaseous phase (except for rare cases) • Complex reaction mechanisms are made of a large number of elementary steps • The elementary steps mostly imply neutral species (molecules, radicals, atoms, but rarely ions) • The elementary steps are mostly bimolecular, but can be also uni- or trimolecular (as in next table) 33

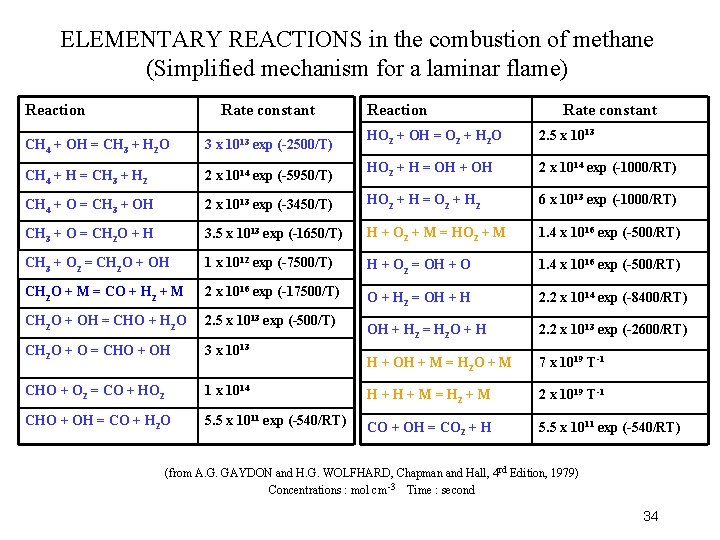
ELEMENTARY REACTIONS in the combustion of methane (Simplified mechanism for a laminar flame) Reaction Rate constant 1013 exp (-2500/T) Reaction Rate constant HO 2 + OH = O 2 + H 2 O 2. 5 x 1013 CH 4 + OH = CH 3 + H 2 O 3 x CH 4 + H = CH 3 + H 2 2 x 1014 exp (-5950/T) HO 2 + H = OH + OH 2 x 1014 exp (-1000/RT) CH 4 + O = CH 3 + OH 2 x 1013 exp (-3450/T) HO 2 + H = O 2 + H 2 6 x 1013 exp (-1000/RT) CH 3 + O = CH 2 O + H 3. 5 x 1013 exp (-1650/T) H + O 2 + M = HO 2 + M 1. 4 x 1016 exp (-500/RT) CH 3 + O 2 = CH 2 O + OH 1 x 1012 exp (-7500/T) H + O 2 = OH + O 1. 4 x 1016 exp (-500/RT) CH 2 O + M = CO + H 2 + M 2 x 1016 exp (-17500/T) O + H 2 = OH + H 2. 2 x 1014 exp (-8400/RT) CH 2 O + OH = CHO + H 2 O 2. 5 x 1013 exp (-500/T) OH + H 2 = H 2 O + H 2. 2 x 1013 exp (-2600/RT) CH 2 O + O = CHO + OH 3 x 1013 H + OH + M = H 2 O + M 7 x 1019 T-1 CHO + O 2 = CO + HO 2 1 x 1014 H + M = H 2 + M 2 x 1019 T-1 CHO + OH = CO + H 2 O 5. 5 x 1011 exp (-540/RT) CO + OH = CO 2 + H 5. 5 x 1011 exp (-540/RT) (from A. G. GAYDON and H. G. WOLFHARD, Chapman and Hall, 4 rd Edition, 1979) Concentrations : mol cm -3 Time : second 34

3. Characteristics of combustible mixtures How to evaluate the kinetic parameters at high temperature ? • Experimentally in a: – Flow reactor – Shock tube – Fast compression machine … • On a theoretical basis • By coupling the experimental study and a simulation (with a sensitivity study) 35

4. Reaction mechanisms in flames or in combustion processes 1. Basic chemical kinetics 2. Elementary reactions 3. Characteristics of combustible mixtures 4. Reaction mechanisms in flames or in combustion processes 4. 1 – Linear-chains reactions 4. 2 – Branching-chains reactions 4. 3 – Conclusion on reaction mechanisms 4. 4 - Numerical resolution of the system of equations 5. Formation and destruction of nitrogen oxides 36

4. Reaction mechanisms in flames or in combustion processes 4. 1 – Linear-chains reactions Discovery of complex mechanisms • Bodenstein 1906 : ½ H 2 (g) + ½ Br 2 (g) HBr (g) Δr. H° 298 = -30, 4 k. J mol-1 • Reaction with non-defined order : v = d[HBr]/dt = k [H 2] [Br 2]1/2 /(1 + k’ [HBr]/[Br 2]) • • • Strictly a gas-phase reaction: not a catalytic reaction, no heterogeneous effect, no effect of the reactor wall HBr added to reactants makes the reaction rate decrease (HBr is an inhibitor for the reaction) Linear-chains mechanism: Polanyi et al. , 1919 Steady-state approximation applied to atoms, radicals, intermediate species R: d[R]/dt = 0 Since they appear and disappear, [R] = constant 37 with t

4. Reaction mechanisms in flames or in combustion processes 4. 1 – Linear-chains reactions H 2 + Br 2 2 HBr Overall reaction: Detailed mechanism: Br 2 + M H 2 + Br Br 2 + H H + HBr 2 Br + M • • • 2 Br + M HBr + H HBr + Br H 2 + Br Br 2 + M initiation propagation Kinetic propagation chain inhibition termination/rupture Calculated overall reaction rate v corresponds to the experimental results of Bodenstein It is a linear-chains mechanism: discovered by Polanyi et al. , 1919 Chains carriers: H et Br: for them, we apply the steady-state approximation Steady-state approximation applied to atoms, radicals, intermediate species: Since H and Br appear and disappear during the reaction, [H] = constant ; [Br] = constant d[H]/dt = 0 and d[Br]/dt = 0 38

4. Reaction mechanisms in flames or in combustion processes 4. 2 - Branching chains reactions H 2 (g) + ½ O 2 (g) H 2 O (g) • The experiments show that, for this stoichiometric reaction, the curve of P = f (T) : – is an inversed S-curve with three « explosion limits » between autoignition (slow oxidation) and explosion (very rapid reaction) – shows regions of autoignition and regions of explosion 39

4. Reaction mechanisms in flames or in combustion processes 4. 2 - Branching chains reactions H 2 (g) + ½ O 2 (g) H 2 O (g) • Simplified mechanism: H 2 + O 2 H 2 + M H 2 + OH H + O 2 O + H 2 H + O 2 + M H 2 + HO 2 H + wall 2 OH 2 H+M H 2 O + H OH + O OH + H HO 2 + M H 2 O + OH recombination (or O, OH, HO 2) Initiation Propagation (pr) Chain branching Homogeneous rupture Propagation (less efficient) Heterogeneous rupture at the wall • Detailed mechanism: 37 steps, 9 species (including H, O, OH, HO 2, H 2 O 2, O 3) • Reaction rate vr: vr = d[H 2 O]/dt = kpr [H 2][OH] 40

4. Reaction mechanisms in flames or in combustion processes 4. 2 - Branching chain reactions A R • + P (initiation) vi = {d[R • ]/dt}i (propagation) vp = kp [R • ] ; {d[R • ]/dt}p = 0 R • + A αR • (branching) R • + A B (termination) vt = kt [R • ] = {-d[R • ]/dt)}t A: reactant P: product vb = kb [R • ] = (d[R • ]/dt)/(1 -α) [R • ] : intermediate species Rate of the variation of the intermediate species concentration R • : (d[R • ]/dt) = vi + (α-1)vb – vt = vi + {kb(α-1) - kt }[R • ] = vi + Φ[R • ] 41

4. Reaction mechanisms in flames or in combustion processes 4. 2 - Branching chain reactions Conditions of explosion • d[R • ]/dt = vi + Φ [R • ] * Stationary state possible if Φ < 0 [R • ]steady = - vi /Φ • Integration of d[R • ]/dt = vi + Φ [R • ] = (vi /Φ) [exp(Φt) - 1)] • Φ = kb(α-1) - kt = transmission factor with t: time Overall rate : Vr = + d[P]/dt Vr = k. P [R • ] = k. P (vi /Φ) [exp(Φt) - 1)] 42

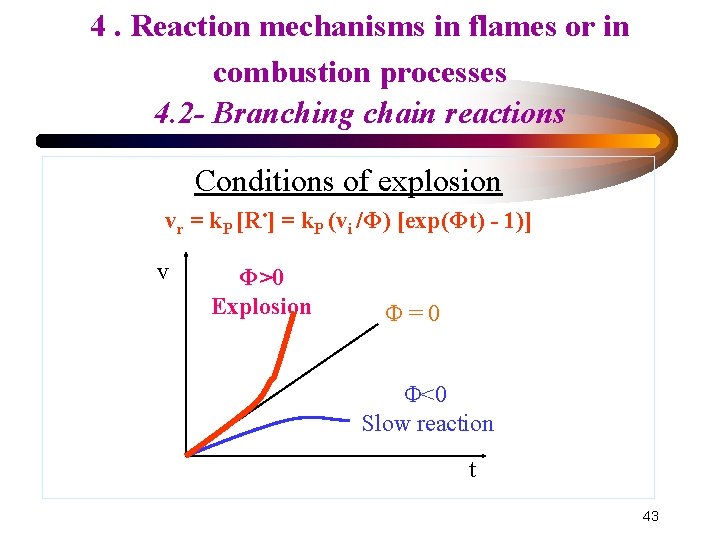
4. Reaction mechanisms in flames or in combustion processes 4. 2 - Branching chain reactions Conditions of explosion vr = k. P [R • ] = k. P (vi /Φ) [exp(Φt) - 1)] v Φ>0 Explosion Φ=0 Φ<0 Slow reaction t 43

4. Reaction mechanisms in flames or in combustion processes 4. 3 - Conclusion on reaction mechanisms • Complex mechanisms – Decomposed into many elementary steps • Reactions between neutral species – Predominance of bimolecular reactions – Presence of uni- and trimolecular reactions (but few) • Very low ionized medium – Combustion in air: small quantities of NO+ • Non-linear systems of equations – Numerical resolution of stiff systems 44

4. Reaction mechanisms in flames or in combustion processes 4. 4 - Numerical resolution of the system of equations Chemkin Evolution of the concentrations of the chemical species in different reactors • • Shock tube (SENKIN) Laminar flame (PREMIX) Perfect Stirred Reactor (PSR) etc… Example : methane/air 45

SENKIN Concentration profiles behind a shock wave for the mixture: CH 4 / air 46

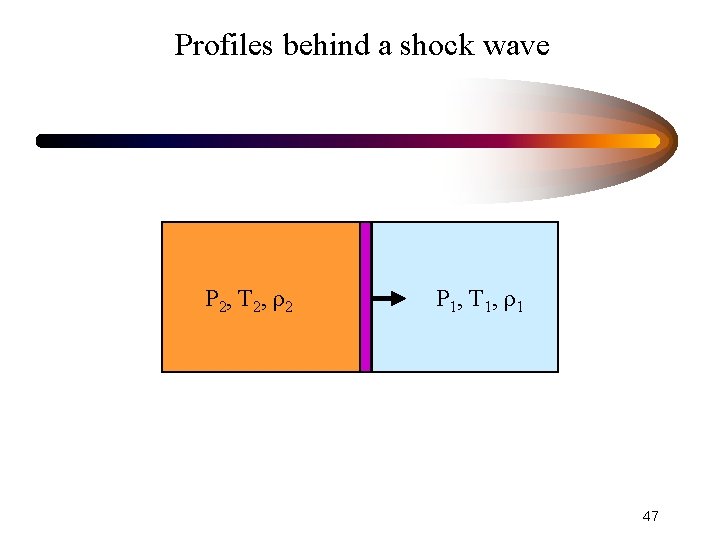
Profiles behind a shock wave P 2, T 2, ρ2 P 1, T 1, ρ1 47

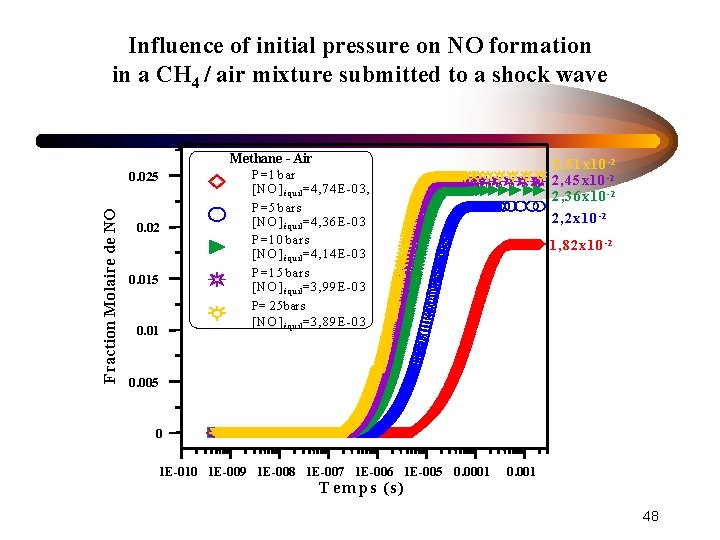
Influence of initial pressure on NO formation in a CH 4 / air mixture submitted to a shock wave Methane - Air Fraction Molaire de NO 0. 025 0. 02 0. 015 0. 01 2, 5 1 x 10 -2 2, 4 5 x 10 -2 2, 3 6 x 10 -2 P= 1 bar [N O ] équil = 4, 74 E -03, P= 5 bars [N O ] équil = 4, 36 E -03 P= 10 bars [N O ] équil = 4, 14 E -03 P= 15 bars [N O ] équil = 3, 99 E -03 P= 25 bars [N O ] équil = 3, 89 E -03 2 , 2 x 10 -2 1 , 8 2 x 1 0 -2 0. 005 0 1 E-010 1 E-009 1 E-008 1 E-007 1 E-006 1 E-005 0. 0001 T em p s (s) 0. 001 48

PREMIX Concentration profiles through a laminar flame front for the mixture: CH 4 / air 49

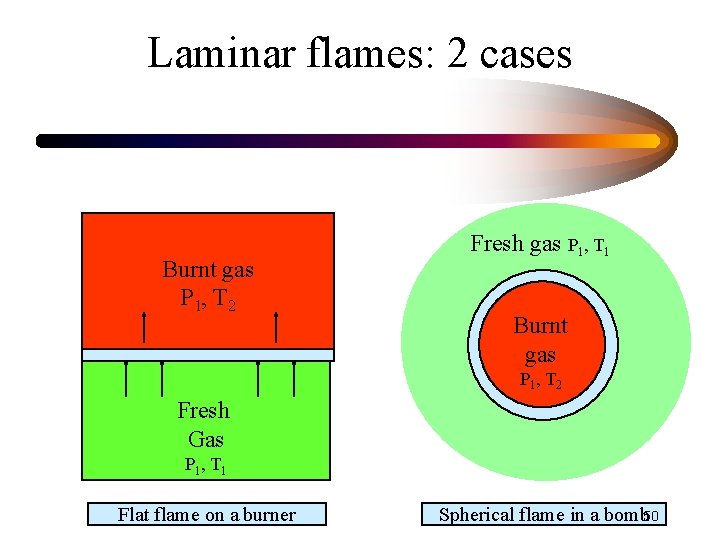
Laminar flames: 2 cases Burnt gas P 1, T 2 Fresh gas P 1, T 1 Burnt gas P 1 , T 2 Fresh Gas P 1 , T 1 Flat flame on a burner Spherical flame in a bomb 50

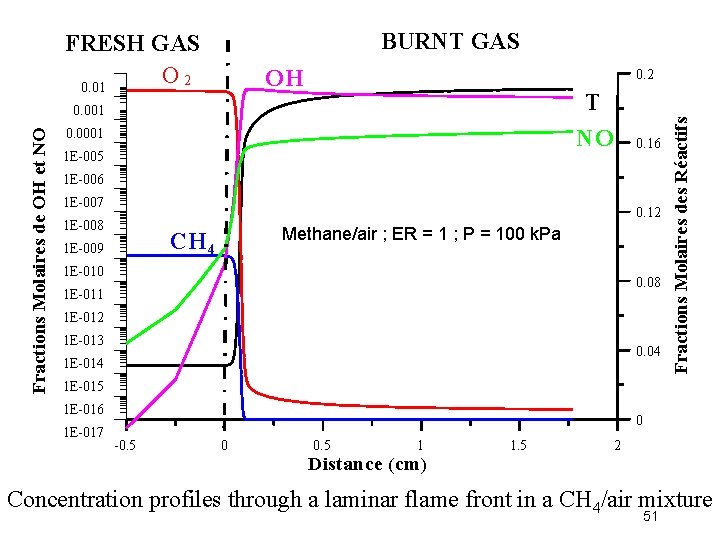
BURNT GAS OH 0. 2 T NO Fractions Molaires de OH et NO 0. 001 0. 0001 1 E-005 0. 16 1 E-007 0. 12 1 E-008 Methane/air ; ER = 1 ; P = 100 k. Pa CH 4 1 E-009 1 E-010 0. 08 1 E-011 1 E-012 1 E-013 0. 04 1 E-014 Fractions Molaires des Réactifs FRESH GAS O 2 0. 01 1 E-015 1 E-016 1 E-017 0 -0. 5 0 0. 5 1 1. 5 2 Distance (cm) Concentration profiles through a laminar flame front in a CH 4/air mixture 51

52

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO • Nitric oxide NO is an important minor species in combustion, because of its contribution to air pollution • In the combustion of fuels that contains no nitrogen, NO is formed by 4 different chemical mechanisms that involve N 2 from the air: – – The thermal-NO mechanism (called the ‘Zeldovich mechanism’ The prompt-NO mechanism (called the ‘Fenimore mechanism’) The N 2 O-intermediate mechanism The NNH-intermediate mechanism • Certain fuels contain N in their molecular structure, like coal that contains bound N up to ~ 2% by mass. In this case, there is a 5 th mechanism for the bound nitrogen in such fuels that converts nitrogen into HCN (hydrogen cyanide) and NH 3 (ammonia): – The fuel-NO mechanism 53

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 1 Mechanism of thermal-NO (1): called Zeldovich mechanism – Proposed by Zeldovich in 1946, completed by Fenimore in 1971 – It concerns the formation of NO from the molecular nitrogen contained in air – It dominates in high-T combustion over a wide range of equivalence ratios (1) N 2 + (-1)NO + N (2) NO + (-2)N + O 2 (3) N + (-3)NO + H O N 2 + O NO + OH N + NO + N θ 1 = 38200 K (= Ea/R) O θ-1 = 0 K N + O 2 θ 2 = 19500 K O θ-2 = 3100 K NO + H θ 3 = 0 K OH θ-3 = 20000 K 54

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 1 Mechanism of thermal-NO (2): called the ‘Zeldovich mechanism’ (1) (-1) (2) (-2) (3) (-3) N 2 NO NO N N NO + + + O N O O 2 OH H NO N 2 N NO NO N + + + N O O 2 O H OH θ 1 = 38200 K (= Ea/R) θ-1= 0 K θ 2 = 19500 K θ-2= 3100 K θ 3 = 0 K θ-3= 20000 K • Reaction (1) is the limiting step (that is the slower one, except at high temperature) and has the highest Ea • It determines the overall reaction rate 55

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 1 Mechanism of thermal-NO (3): called the ‘Zeldovich mechanism’ (1) (-1) (2) (-2) (3) (-3) N 2 NO NO N N NO + + + O N O O 2 OH H NO N 2 N NO NO N + + + N O O 2 O H OH θ 1 = 38200 K (= Ea/R) θ-1= 0 K θ 2 = 19500 K θ-2= 3100 K θ 3 = 0 K θ-3= 20000 K • Reduction of thermal-NO: – Decrease the flame temperature, the residence time – Decrease the oxygen concentration in the region of the temperature peak 56

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 2 Mechanism of fuel-NO (1) – Proposed by Fenimore et Jones, 1961 – It concerns the formation of NO from the nitrogen N contained in the combustible molecule (amine group or pyridinic group). Ex: coal (contains bound N up to ~ 2% by mass) – The C-N bond is much weaker than N-N bond: this mechanism of fuel-NO formation will be easier at lower temperatures than that one for thermal-NO 57

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 2 Mechanism of fuel-NO (2) – Rapid reactions lead to formation of HCN (cyanhydric acid), that reacts with atomic oxygen: HCN + O NCO + H CN + OH NH + CO – CN radical produces NCO via: CN CN + O 2 NCO + OH NCO + H 58

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 2 Mechanism of fuel-NO (3) In an oxidative medium, NCO forms NO and CO via: NCO + OH NO + CO + H NCO + O NO + CO • the quantity of NO formed does not depend on the molecules containing N, since they all rapidly form HCN, NH 3 and their fragments inside the flame • The oxidation of these compounds leads to NO 59

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 3 Mechanism of prompt-NO (1): called the ‘Fenimore mechanism’ – Proposed by Fenimore in 1970, and confirmed by many researchers – It concerns the formation of NO from molecular nitrogen N 2 – It is particularly important in rich combustion – N 2 reacts in the flame front with the hydrocarbonated radicals CHi (i = 0, 1, 2) in the rich mixture – The formation of prompt-NO is dominated by the reaction: N 2 + CH ↔ HCN + N θ = 9000 K followed by the mechanism of fuel-NO for the consumption of HCN and the formation de NO in an oxidative medium 60

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 3 Mechanism of prompt-NO (2): called the ‘Fenimore mechanism’ – At the opposite of the mechanism of thermal-NO formation, prompt-NO is produced at relatively low temperature (about 1000 K) – Generally, the quantity of prompt-NO formed is low, in comparison to that issued from Zeldovich mechanism (or thermal -NO) – To limit the quantity of prompt NO formed, the best is to increase the mixing rate of the combustible molecule with air 61

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 4 Mechanism of formation of NO via N 2 O • Proposed by Malte and Pratt in 1974 • At relatively low temperature and high pressure, N 2 O (nitrogen hemioxide or protoxide) is formed via: N 2 + O + M ↔ N 2 O + M • N 2 O formation is followed by reactions of O and H with N 2 O giving NO: N 2 O + O ↔ 2 NO N 2 O + H ↔ NO + NH • N 2 O mechanism plays an important role in the production of NO in very lean (Φ < 0. 8), low-T combustion processes 62

5. Formation of nitrogen oxides in combustion 5. 1 - Mechanisms of formation of NO 5. 1. 4 Mechanism of formation of NO via NNH • Proposed by Bozzelli and Dean, 1995 • This mechanism implies NNH radical and oxygen atom: NNH + O NO + NH • This reaction can be important in the flame front where the O concentration is high 63

5. Formation of nitrogen oxides in combustion 5. 2 - Mechanisms of formation of NO 2 • In the atmosphere, nitric oxide NO ultimately oxidizes to form nitrogen dioxide NO 2 which is important for the production of acid rain and photochemical smog • Many combustion processes also emit significant fractions of their total nitrogen oxides as NO 2 • The elementary reactions responsible forming NO 2 prior to the exhausting of combustion products in the atmosphere are : 64

5. Formation of nitrogen oxides in combustion 5. 2 - Mechanisms of formation of NO 2 NO + HO 2 NO 2 + H NO 2 + OH NO + O 2 formation destruction where the HO 2 radical is formed as: H + O 2 + M HO 2 + M • The HO 2 radicals are formed in relatively low-T regions • NO 2 formation occurs when NO molecules from high-T regions diffuse or are transported into the HO 2 -rich regions • The reactions leading to the NO 2 destruction are active at high T, thus preventing the formation of NO 2 in high-T zones 65

66

6. Kinetics and combustion of hydrogen 1. Basic chemical kinetics 2. Elementary reactions 3. Characteristics of combustible mixtures 4. Reaction mechanisms in flames or combustion mechanisms 5. Formation of nitrogen oxides in combustion 6. Kinetics and combustion of hydrogen Chemical systems containing hydrogen are important for : 5. 1 - Spatial propulsion 5. 2 - Hydrogen hazard 67

Chemical systems containing hydrogen • Oxidation mechanism well known • Main steps governing the combustion: H + O 2 O + H 2 OH + H 2 H + O 2 + M OH + O OH + H H 2 O + H HO 2 + M • Peculiar cases – Supersonic combustion (Superstatoreactors) – Very lean H 2 flames 68

69

5. 1 - Spatial propulsion Kinetics and conception of a superstatoreactor Configuration of a supersonic combustion statoreactor Fuel: H 2 Oxidant: air Hypersonic > 6 times the sound speed 70

Combustion in a supersonic flow regime Energy efficiency limited by : • the dynamics of reactants mixing • the reaction kinetics Re-evaluation of rate constants of elementary chemical reactions, that are important in the combustion of hydrogen in a supersonic flow regime 71

Important elementary reactions in the combustion of hydrogen in a supersonic flow regime • Reactions of initiation, propagation and branching • Reactions of trimolecular recombination X+Y+M XY + M X and Y: atomic or radical species (H, O, OH) M: collision partner (H 2, O 2, N 2 , H 2 O) at T > 2700 K Rate constants given at ± 50 % for M = N 2, O 2, H 2 O at T > 2700 K [Baulch et al, 1994] 72

Experimental methods • Shock tube Gaseous mixture is rapidly submitted to high temperature and pressure, behind a shock wave • ARAS (Atomic Resonance Absorption Spectroscopy) Direct measurement of absorption profiles of O atoms in shocked gas is made Time-resolved evolution of O atoms 73

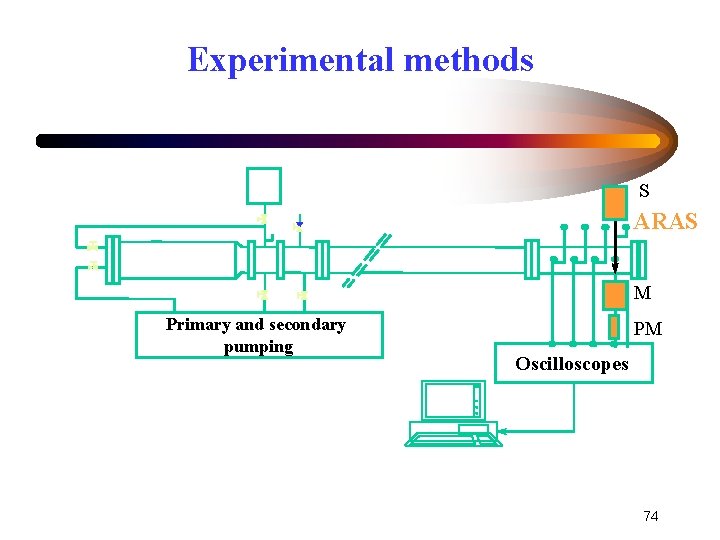
Experimental methods S ARAS M Primary and secondary pumping PM Oscilloscopes 74

Methodology Determination of rate constant kd: O 2 + M ↔ 2 O + M • Adjustment of kd value in the detailed mechanism from the experimental determination of [O] = f (t) • Determination of kr from Keq = kd / kr Expression of kd and kr versus temperature: k = A Tn exp (- θ / T) 75

Determination of the rate constant: O + H 2 → OH + H • From the experimental variation of [O] = f (t) • Taking into account of the rate constants of other elementary reactions: N 2 O + Ar = N 2 + O + Ar OH + Ar = H + O + Ar H 2 + Ar = 2 H + Ar OH + H 2 = H 2 O + H H + O 2 = OH + O Δk/k = ± 40 % Δk/k = ± 50 % Δk/k = ± 30 % Δk/k = ± 20 % ± 8 % uncertainty on k (O + H 2) • Comparison with literature 76

Influence on the rate constant: O 2 + N 2 → 2 O + N 2 of the experimental parameters uncertainties Experimental parameters Temperature Pressure Mixture composition Calibration curve ki of other elementary reactions Parasitic absorption Uncertainties on k(O 2 + N 2) ± 7 % at 2800 K ; ± 8 % at 3200 K ± 8% ± 7% ± 18 % ± 25 % at 2800 K ; ± 29 % at 3200 K negligible Total uncertainty estimated to ± 35 % 77

Shock tube coupled to ARAS Re-evaluation of rate constants of the elementary reactions that are important in H 2 combustion in a supersonic flow regime: (Ph. D Thesis: V. Naudet, 1998 ; S. Javoy, 2001) O + H 2 → OH + O 2 + M → 2 O + H + OH + M → H 2 O + H + O + M → OH + H M M M with M = Ar and N 2 with M = Ar and H 2 O with M = Ar and N 2 Improvement of energy efficiency 78

5. 2 – Hydrogen hazard Hydrogen as a fuel for transportation • Leak hazard (in tunnels, parking lots…) • Explosion hazard in a confined medium with obstacles → Role of H 2 concentration gradient on the flame behavior → Impossibility of introducing a detailed mechanism in turbulent combustion codes Introduction of the normal flame speed SL° = f (P, T, Φ) in the simulation codes of the turbulent flame propagation in a congested medium 79

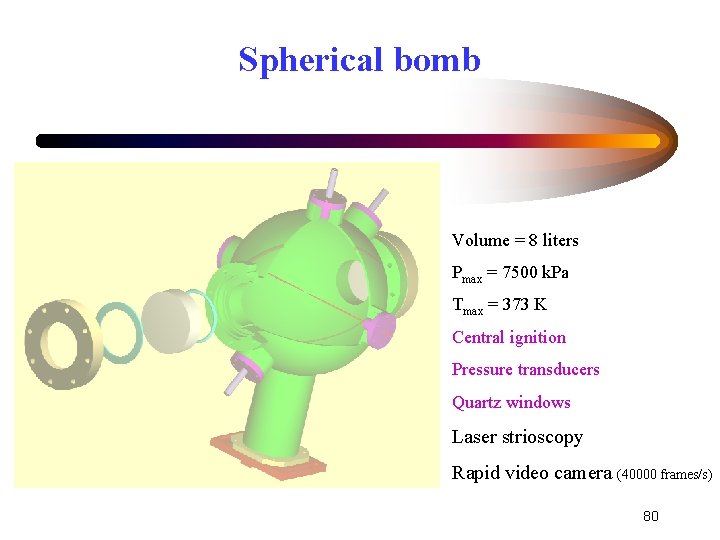
Spherical bomb Volume = 8 liters Pmax = 7500 k. Pa Tmax = 373 K Central ignition Pressure transducers Quartz windows Laser strioscopy Rapid video camera (40000 frames/s) 80

Propagation of a H 2/air flame in a spherical bomb 20% H 2 + 68% air + 12% CO 2 ; 298 K ; 100 k. Pa 81

Normal flame speeds: comparison between experiments and models Normal flame speed (cm/s) Hydrogen molar fraction 82

Comparison on the more sensitive steps, for several mechanisms: k = f (1/T) 83

Normal flame speed SL° = f (x. H 2) for H 2 – air mixtures SL° (m/s) Coupling Measurement/Simulation SL° data for very lean mixtures near the observation limits of highly accelerated flames (Ph. D Thesis: F. Malet, 2005) Hydrogen volume fraction 84

Analysis of hydrogen hazard (Hydrogen as a fuel for transportation) • SL° = f (x. H 2) for H 2 – air mixtures, near the flammability limit, thanks to the coupling of: - measurements of spatial speeds in a spherical bomb → SL with zero stretching (N 2 replaced by He) - calculation of SL implying a detailed kinetic model • Evaluation of flame acceleration effects: made possible with the introduction of SL° in the 3 D codes 85

86