Fundamental Theorem of Algebra TS Demonstrating understanding of

Fundamental Theorem of Algebra TS: Demonstrating understanding of concepts Warm-Up: T or F: A cubic function has at least one real root. T or F: A polynomial function can have no complex solutions. T or F: A polynomial function could have only one imaginary solution. T or F: A polynomial could have root 2 as its only irrational solution.

The Fundamental Theorem of Algebra If f(x) is a polynomial of degree n, where n > 0, then f has at least one zero in the complex number system. Linear Factorization Theorem If f(x) is a polynomial of degree n where n > 0, f has precisely n linear factors f(x) = an(x – c 1)(x – c 2)∙∙∙(x – cn) where c 1, c 2, …, cn are complex numbers.

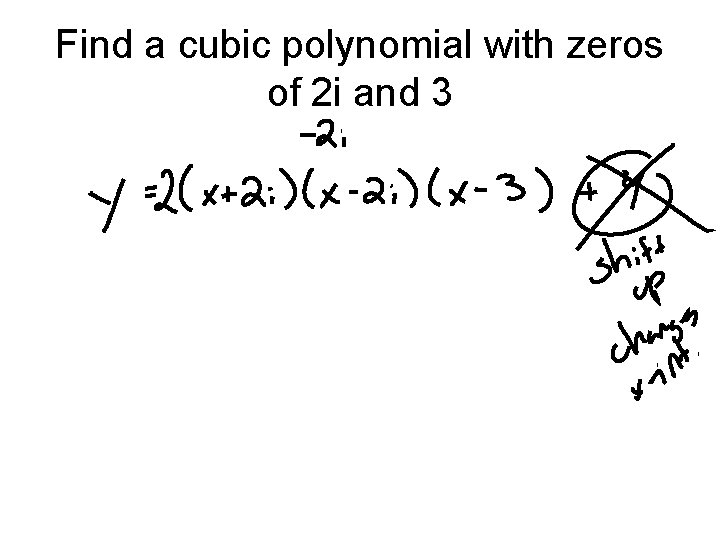
Find a cubic polynomial with zeros of 2 i and 3

Find the quartic polynomial with zeros -√ 2 and i, which passes through (1, 6)

Factoring Polynomials so they are irreducable over the rationals, reals and complex zeros. Factor each: a) x 4 – x 2 – 20

Factoring Polynomials so they are irreducable over the rationals, reals and complex zeros. Factor each: b) x 4 – 3 x 3 – x 2 – 12 x – 20 (Hint: x 2 + 4 is a factor)

You Try: 1) If -1 – 3 i is a zero of x 3 + 4 x 2 + 14 x + 20, find the other zeros 2) Factor the following: x 4 + 6 x 2 – 27 a) Irreducible over the rationals: b) Irreducible over the reals: c) Irreducible over the complex: