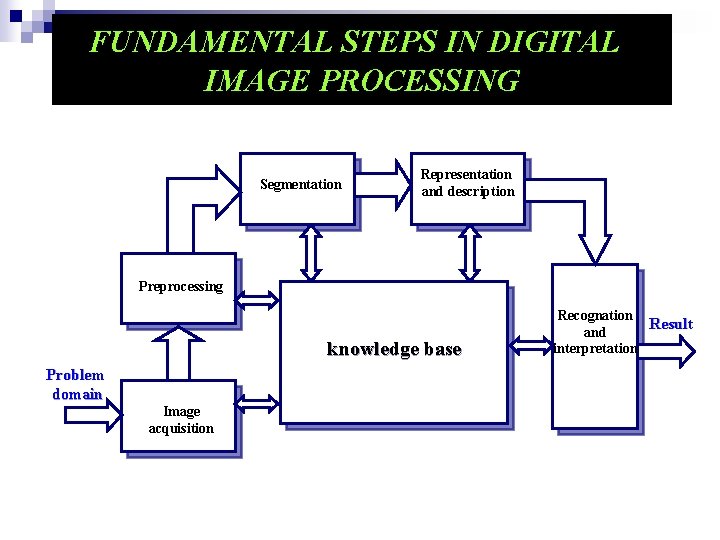
FUNDAMENTAL STEPS IN DIGITAL IMAGE PROCESSING Segmentation Representation

FUNDAMENTAL STEPS IN DIGITAL IMAGE PROCESSING Segmentation Representation and description Preprocessing knowledge base Problem domain Image acquisition Recognation Result and interpretation

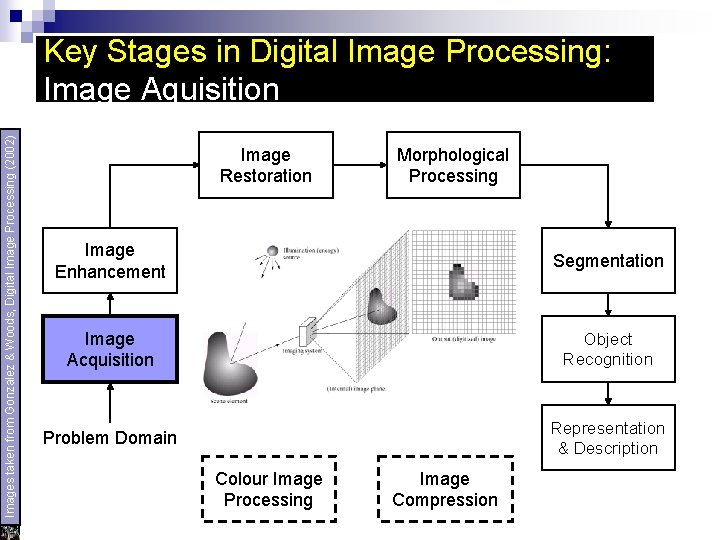
Image Acquisition Imaging sensor & capability to digitize the signal collected by the sensor: Video camera u Digital camera u Conventional camera & analog-todigital converter u

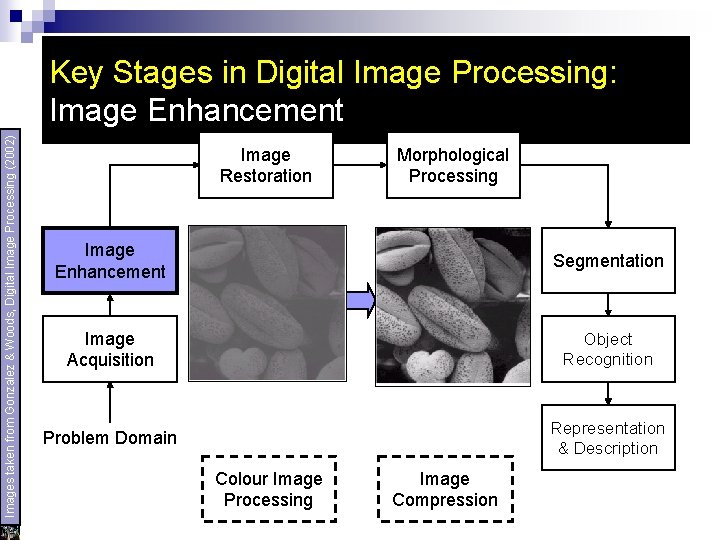
Preprocessing To improve the image to ensure the success of further processes: u u Enhancing contrast Removing noise

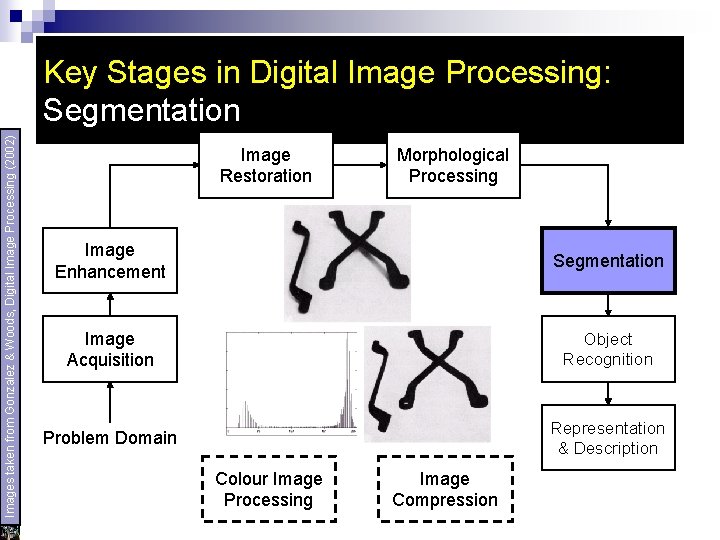
Segmentation To partition the image into its constituent parts (objects) u Autonomous ﻣﺴﺘﻘﻞ segmentation (very difficult) – can facilitate or disturb subsequent processes u Output (representation): – raw pixel data, depicting either boundaries or whole regions (corners vs. texture for example) – need conversion to a form suitable for computer processing u (Description)

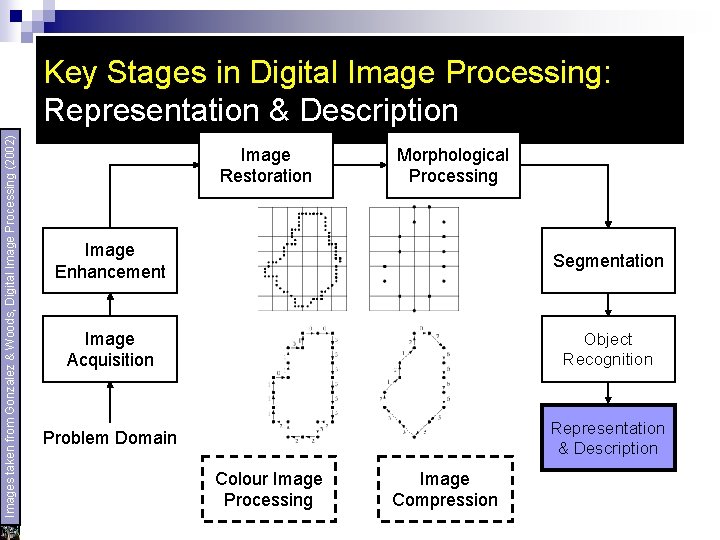
Representation & Description Feature selection (description) deals with extracting: u Features that result in quantitative information of interest or u Features that are important for differentiating one class of objects from another

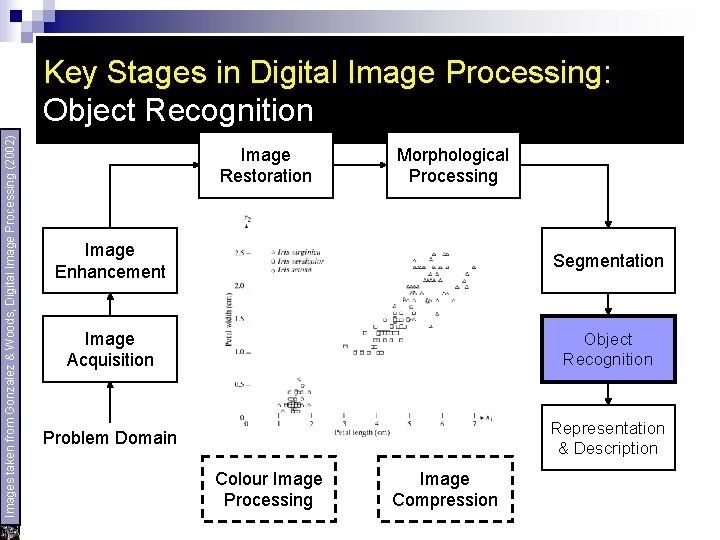
Recognition & Interpretation u To assign a label to an object based on information provided by the descriptors u To assign meaning to a group of recognized objects

Knowledge Base Knowledge database: Guides the operation of each processing module and controls the interaction between modules.

Key Stages in Digital Image Processing Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Image Aquisition Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Image Enhancement Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

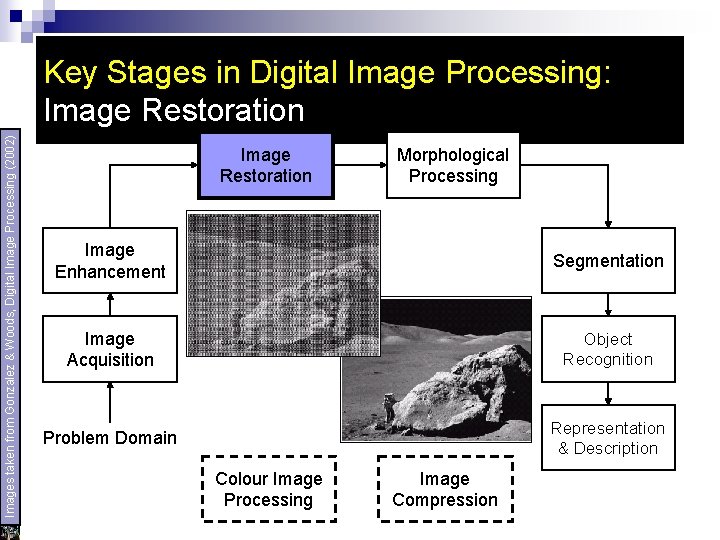
Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

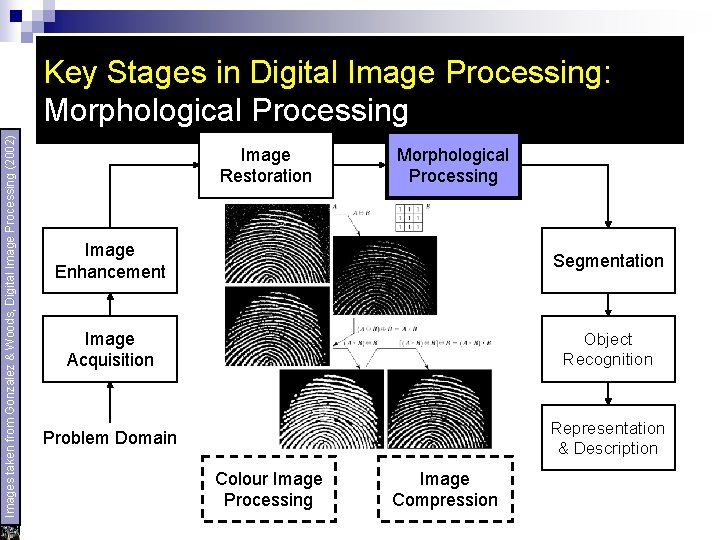
Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Morphological Processing Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Segmentation Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Object Recognition Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Images taken from Gonzalez & Woods, Digital Image Processing (2002) Key Stages in Digital Image Processing: Representation & Description Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Key Stages in Digital Image Processing: Image Compression Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

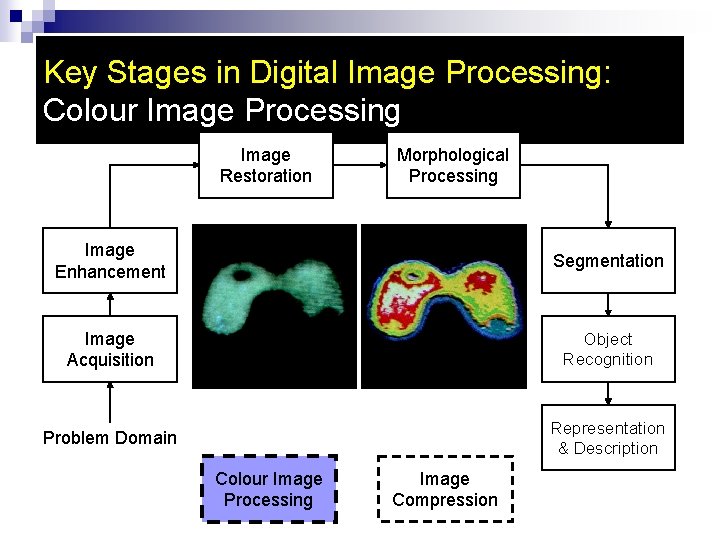
Key Stages in Digital Image Processing: Colour Image Processing Image Restoration Morphological Processing Image Enhancement Segmentation Image Acquisition Object Recognition Problem Domain Representation & Description Colour Image Processing Image Compression

Digital Image Definitions A digital image a[m, n] described in a 2 D discrete space is derived from an analog image a(x, y) in a 2 D continuous space through a sampling process that is frequently �������� referred to as digitization. The 2 D continuous image a(x, y) is divided into N rows and M columns.

The intersection of a row and a column is termed a pixel. The value assigned to the integer coordinates [m, n] with {m = 0, 1, 2, . . . , M-1} and {n = 0, 1, 2, . . . , N 1} is a[m, n].

The image has been divided into N = 16 rows and M = 16 columns The value assigned to every pixel is the average brightness in the pixel rounded to the nearest integer value. The process of representing the amplitude ﻧﻄﺎﻕ ﻭﻣﺪﻯ of the 2 D signal at a given coordinate as an integer value with L different gray levels is usually referred to as amplitude quantization or simply quantization. ﺣﺴﺎﺏ ﺍﻟﻜﻢ ﻣﻬﻢ ﺟﺪﺍ

Why Digital? n “Exactness” ﺍﻟﺪﻗﺔ ¨ Perfect reproduction without degradation ﻋﺪﻡ ﺍﻟﺘﻘﻠﻴﻞ ﻣﻦ ﺍﻟﺪﻗﺔ ﻓﻰ ﺣﺎﻟﺔ ﻧﺴﺨﻬﺎ ﺍﻛﺘﺮ ﻣﻦ ﻣﺮﺓ ¨ Perfect duplication of processing result n Convenient & powerful computer-aided processing ¨ Can perform rather sophisticated ﻣﻌﻘﺪ ﻭﻣﺘﻄﻮﺭ processing through hardware or software ¨ Even kindergartners ﺭﻳﺎﺽ ﺍﻃﻔﺎﻝ can do it! n Easy storage and transmission ¨ 1 CD can store hundreds of family photos! ¨ Paperless transmission of high quality photos through network within seconds

Human Vision System n n Image is to be seen. Perceptual Based Image Processing ¨ Focus on perceptually significant information ¨ Discard perceptually insignificant information n Issues: ¨ Biological ¨ Psychophysical

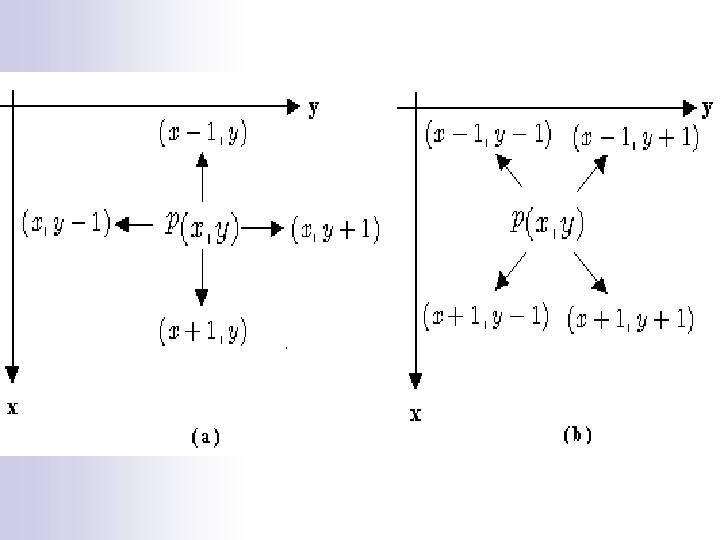
2. 5 Basic Relations between Pixels n Neighbors of a pixel ¨ Horizontal and vertical neighbors. n (x+1, y), (x-1, y), (x, y+1), (x, y-1) ¨ Four diagonal neighbors: ND(p) n (x+1, y+1), (x+1, y-1), (x-1, y+1), (x-1, y-1) ¨ 4 -neighbors of p: N 4(p). ¨ 8 -neighbors of p: N 8(p).

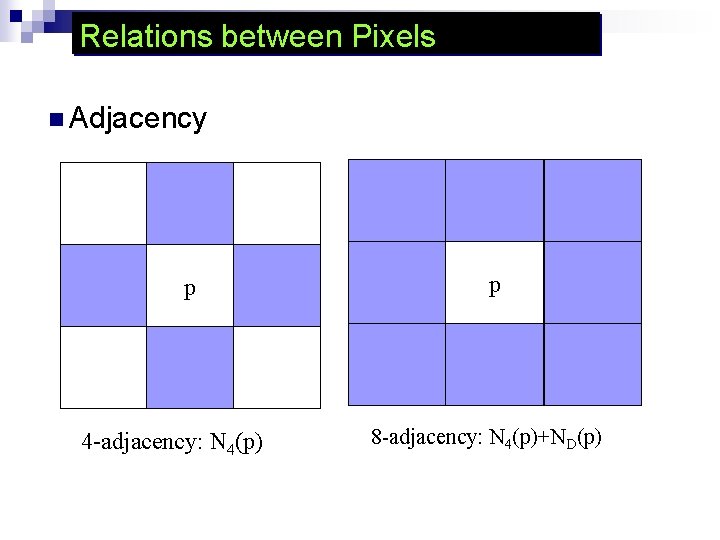
Relations between Pixels n Adjacency p 4 -adjacency: N 4(p) p 8 -adjacency: N 4(p)+ND(p)

m-Adjacency n. A mixed adjacency combines 4 - and 8 adjacency to avoid the ambigities. Multiple 8 -adjacency m-adjacency Two pixels p and q are m-adjacent if (i) q is in N 4(p) or, (ii)q is in ND(p) and N 4(p)∩ N 4(q) has no pixel.

Connectivity n Path: ¨ (x 0, y 0), (x 1, y 1), …, (xn, yn) where (xi, yi) and (xi+1, yi+1) are adjacent. ¨ Closed path: (xn, yn) = (x 0, y 0) ﺍﻧﺘﻬﺖ ﺑﻨﻔﺲ ﺍﻟﺒﺪﺍﻳﺔ n Connectivity: ¨ Two pixels are said connected if they have the same value and there is a path between them. ¨ If a S is a set of pixels, n n For any pixel p in S, the set of pixels that are connected to it is called a connected component of S. If S has only one connected component, S is called a connected set.

Regions n. R is a region if R is a connected set. n The pixel in the boundary (contour) ﻣﺤﻴﻂ has at least one 4 -adjacent neighbor whose value is 0.

n Distance measures ¨ Euclidean distance ¨ City-block distance or D 4 distance. D 4(p, q)= |x - s | + |y - t | ¨ D 8 distance or chessboard distance. D 8(p, q)= max (|x - s |, | y - t |) P=x, y ; q=s, t;

Review Matrices and Vectors To provide background material in support of topics in Digital Image Processing that are based on matrices and/or vectors.

Review: Matrices and Vectors Some Definitions An m×n (read "m by n") matrix, denoted by A, is a rectangular array of entries or elements (numbers, or symbols representing numbers) enclosed typically by square brackets, where m is the number of rows and n the number of columns.

Definitions (Con’t) • The transpose AT of an m×n matrix A is an n×m matrix obtained by interchanging the rows and columns of A. • A square matrix for which AT=A is said to be symmetric. • Any matrix X for which XA=I and AX=I is called the inverse of A. • Let c be a real or complex number (called a scalar). The scalar multiple of c and matrix A, denoted c. A, is obtained by multiplying every elements of A by c. If c = 1, the scalar multiple is called the negative of A.

Definitions (Con’t) A column vector is an m × 1 matrix: A row vector is a 1 × n matrix: A column vector can be expressed as a row vector by using the transpose:

Some Basic Matrix Operations • The sum of two matrices A and B (of equal dimension), denoted A + B, is the matrix with elements aij + bij. • The difference of two matrices, A B, has elements aij bij. • The product, AB, of m×n matrix A and p×q matrix B, is an m×q matrix C whose (i, j)-th element is formed by multiplying the entries across the ith row of A times the entries down the jth column of B; that is,

Some Basic Matrix Operations (Con’t) The inner product (also called dot product) of two vectors is defined as Note that the inner product is a scalar.

Vectors and Vector Spaces A vector space is defined as a nonempty set V of entities called vectors and associated scalars that satisfy the conditions outlined in A through C below. A vector space is real if the scalars are real numbers; it is complex if the scalars are complex numbers. • Condition A: There is in V an operation called vector addition, denoted x + y, that satisfies: 1. x + y = y + x for all vectors x and y in the space. 2. x + (y + z) = (x + y) + z for all x, y, and z. 3. There exists in V a unique vector, called the zero vector, and denoted 0, such that x + 0 = x and 0 + x = x for all vectors x. 4. For each vector x in V, there is a unique vector in V, called the negation of x, and denoted x, such that x + ( x) = 0 and ( x) + x = 0.

Vectors and Vector Spaces (Con’t) • Condition B: There is in V an operation called multiplication by a scalar that associates with each scalar c and each vector x in V a unique vector called the product of c and x, denoted by cx and xc, and which satisfies: 1. c(dx) = (cd)x for all scalars c and d, and all vectors x. 2. (c + d)x = cx + dx for all scalars c and d, and all vectors x. 3. c(x + y) = cx + cy for all scalars c and all vectors x and y. • Condition C: 1 x = x for all vectors x.

Vectors and Vector Spaces (Con’t) We are interested particularly in real vector spaces of real m× 1 column matrices. We denote such spaces by m , with vector addition and multiplication by scalars being as defined earlier for matrices. Vectors (column matrices) in m are written as

Vectors and Vector Spaces (Con’t) Example The vector space with which we are most familiar is the twodimensional real vector space 2 , in which we make frequent use of graphical representations for operations such as vector addition, subtraction, and multiplication by a scalar. For instance, consider the two vectors Using the rules of matrix addition and subtraction we have

Vectors and Vector Spaces (Con’t) Consider two real vector spaces V 0 and V such that: • Each element of V 0 is also an element of V (i. e. , V 0 is a subset of V). • Operations on elements of V 0 are the same as on elements of V. Under these conditions, V 0 is said to be a subspace of V. A linear combination of v 1, v 2, …, vn is an expression of the form where the ’s are scalars.

Vectors and Vector Spaces (Con’t) A vector v is said to be linearly dependent on a set, S, of vectors v 1, v 2, …, vn if and only if v can be written as a linear combination of these vectors. Otherwise, v is linearly independent of the set of vectors v 1, v 2, …, vn.

Vectors and Vector Spaces (Con’t) A set S of vectors v 1, v 2, …, vn in V is said to span some subspace V 0 of V if and only if S is a subset of V 0 and every vector v 0 in V 0 is linearly dependent on the vectors in S. The set S is said to be a spanning set for V 0. A basis for a vector space V is a linearly independent spanning set for V. The number of vectors in the basis for a vector space is called the dimension of the vector space. If, for example, the number of vectors in the basis is n, we say that the vector space is n-dimensional.

Vectors and Vector Spaces (Con’t) An important aspect of the concepts just discussed lies in the representation of any vector in m as a linear combination of the basis vectors. For example, any vector in 3 can be represented as a linear combination of the basis vectors

Definition of Elements n Let A be a set in Z 2. If a = (a 1, a 2) is an element of A, then we write n Similarly, if a isn’t an element of A we write n An arbitrary set in Zn has elements n-tuples as (z 1, z 2, . . . , zn) The set with no elements is called the null or empty set n

What subset is n If every element of a set A is also an element of another set B then A is said to be a subset of B, denoted as Example: X={(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)} and Y={(1, 2), (2, 1), (2, 2), (2, 3), (3, 2)} So,

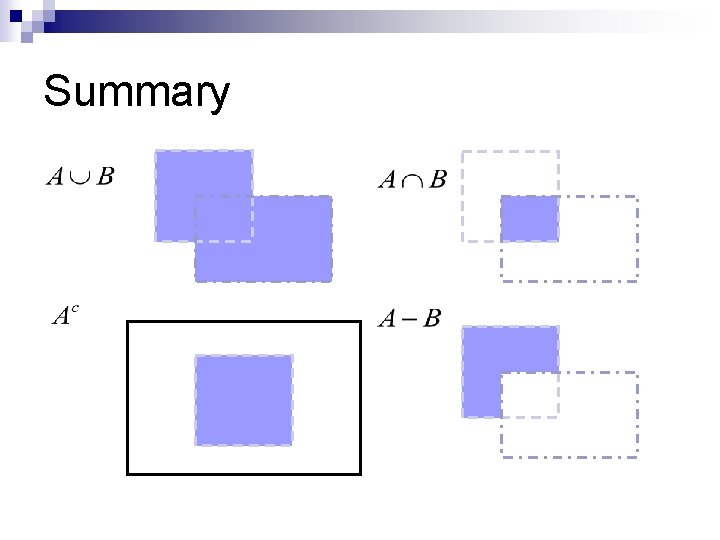
Union Operation n The n Set union of two sets A and B denoted by C is the set of all elements belonging to either A, B, or both

Intersection Operation n The intersection of two sets A and B denoted by n Set D is the set of all elements belonging to both A and B

Mutually Exclusive Property n Two sets A and B is disjoint or mutually exclusive if they have no common elements A B

Complement & Difference n The complement of a set A is the set of elements not contained in A: n Difference of two sets A and B, denoted A-B, is defined as n This is the set of elements that belong to A, but not to B.

Summary

Addition definition n Two additional definition that are used extensively in morphology ¨ The reflection of set B is defined as translation of set A by point z=(z 1, z 2) is defined as

Logic Operations & Binary Images The principal logic operations used in image processing are AND, OR, and NOT (Complement) n Logic operations are preformed on a pixel by pixel basis between corresponding pixels of two or more images (except NOT) n

Logic Operations & Binary Images AND OR

Logic Operations & Binary Images NAND XOR

• Spatial resolution is the smallest discernible detail in an image. • line pair width = 2 W (line width + space) • No. of line pairs per unit distance = 1 / 2 W • Resolution is the smallest number of discernible line pairs per unit distance.

Gray-level resolution refers to the smallest discernible change in gray level (subjective).

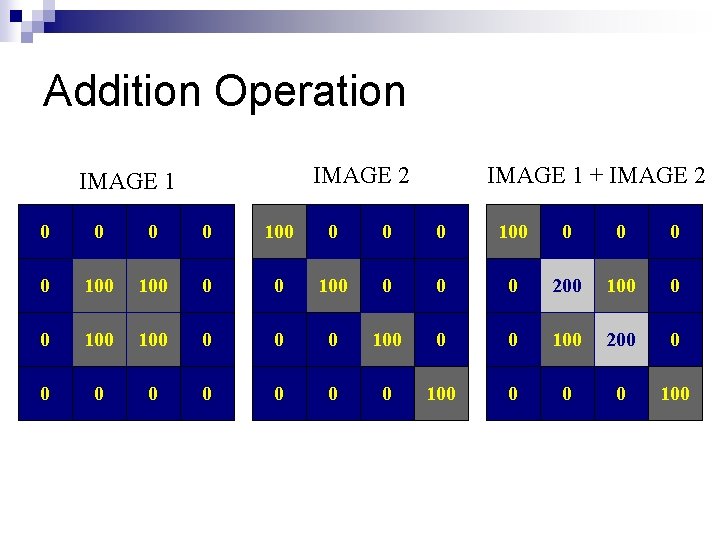
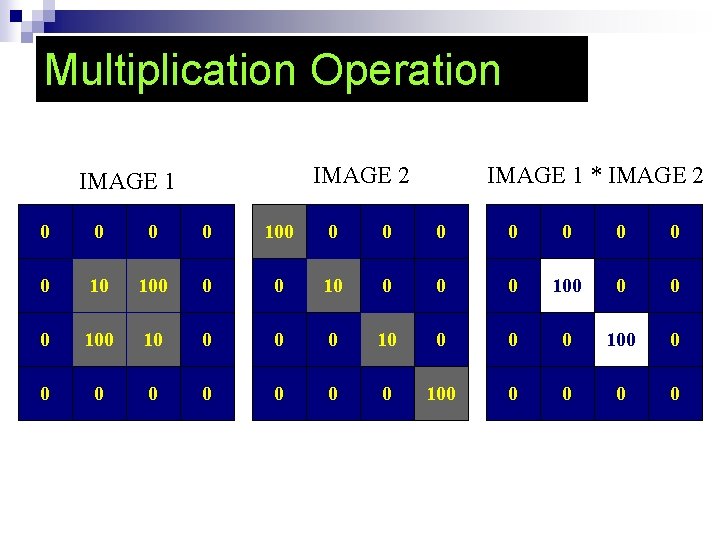
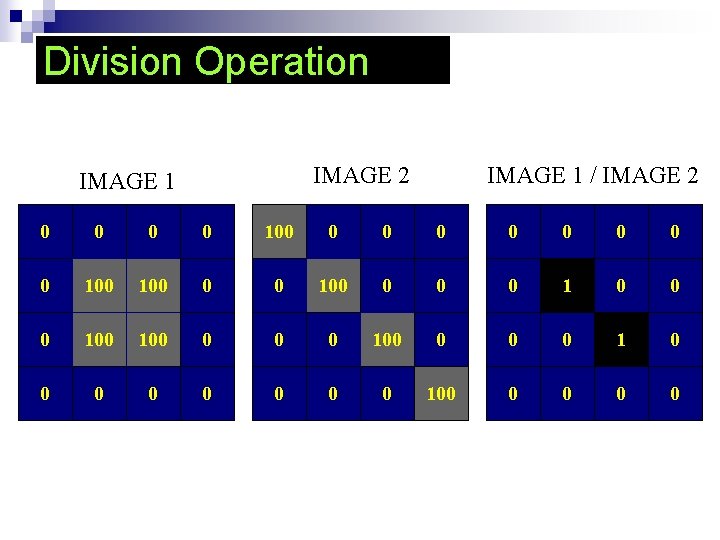
Arithmetic Operation n The arithmetic operations between two pixels p and q are denoted as followed: Subtraction : p – q Addition : p + q Multiplication : p * q Division : p / q

Arithmetic Operation on entire images are carried out pixel by pixel. n If the result is real, truncate its value n If the result is over range, pick the maximum value n If the result if under range, pick the minimum value n

Addition Operation IMAGE 2 IMAGE 1 + IMAGE 2 0 0 100 0 0 100 0 200 100 0 0 100 200 0 0 0 0 100

Subtraction Operation IMAGE 2 IMAGE 1 - IMAGE 2 0 0 100 0 -100 0 0 30 100 0 0 20 0 10 100 0 100 0 0 0 100 0 -100 0 Image subtraction is a basic tool in medical imaging, where it is used to remove static background information

Multiplication Operation IMAGE 2 IMAGE 1 * IMAGE 2 0 0 100 0 -100 0 0 10 0 10000 100 10 0 0 0 10000 100 0 0 0 0 100 0 -100 0

Division Operation IMAGE 2 IMAGE 1 / IMAGE 2 0 0 100 0 -100 0 0 100 0 1 0 0 0 100 0 1 0 0 0 0 100 0 -100 0

Arithmetic Operation Let there is 1 input images p is denoted of a pixel in digital image and c is a constrain. n Addition : p + c n Subtraction : p – c n Multiplication : p * c n Division : p / c

Logic Operation n Principal logic operations used in image processing are AND, OR, and COMPLEMENT, denoted as follows: AND : p AND q OR : p OR q NOT : NOT q

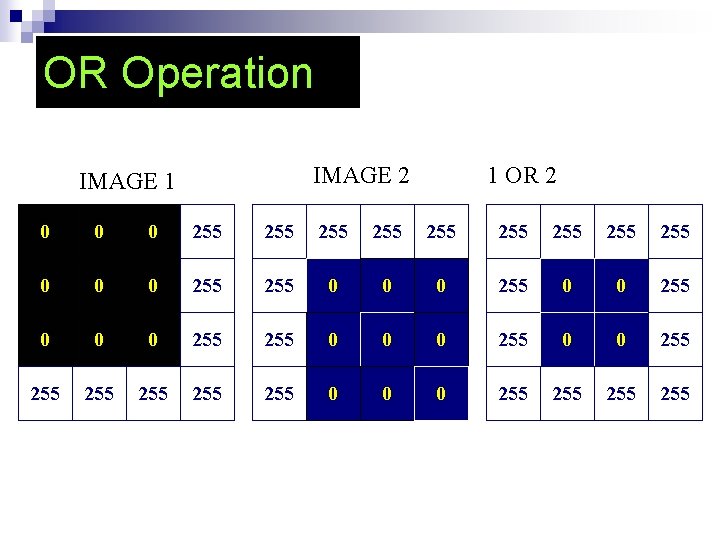
OR Operation IMAGE 2 IMAGE 1 1 OR 2 0 0 0 255 255 255 0 0 0 255 0 0 255 255 255 0 0 0 255 255

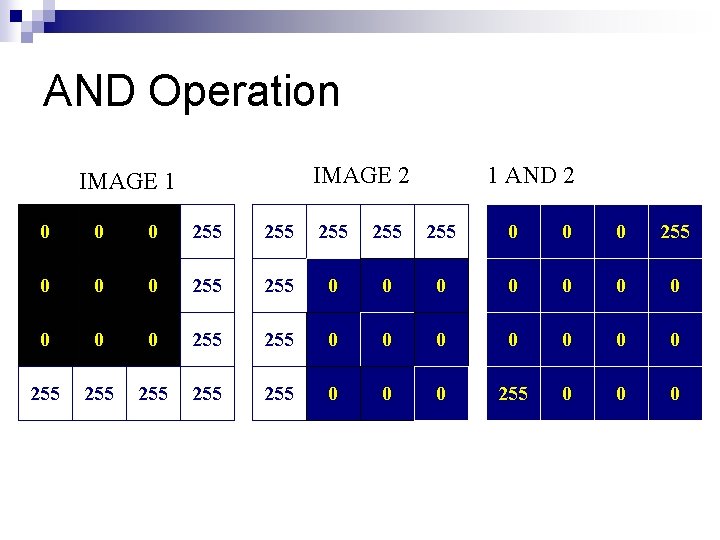
AND Operation IMAGE 2 IMAGE 1 1 AND 2 0 0 0 255 255 255 0 0 0 0 0 255 0 0 0 0 255 255 255 0 0 0

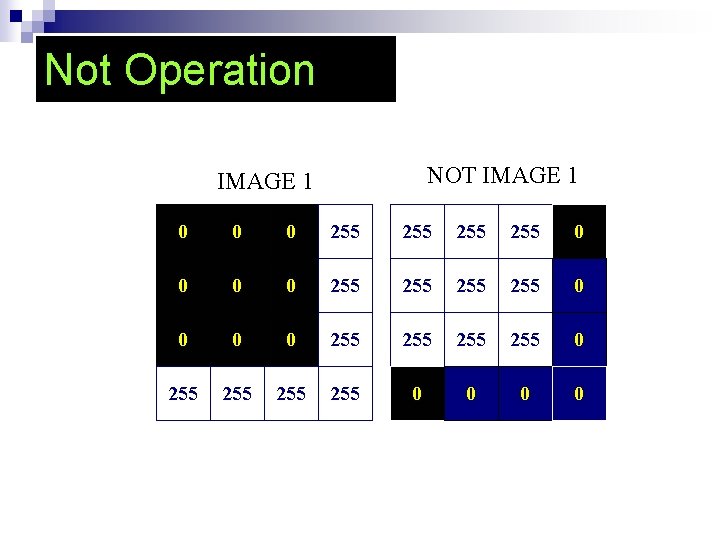
Not Operation NOT IMAGE 1 0 0 0 255 255 255 255 0 0

• 4 -adjacency: if q is in the set N 4(p). • 8 -adjacency: if q is in the set N 8(p). • m-adjacency: if – if q is in the set N 4(p), or – if q is in the set ND(p) and the set N 4(p)∩N 4(q) has no pixels whose values are from V.

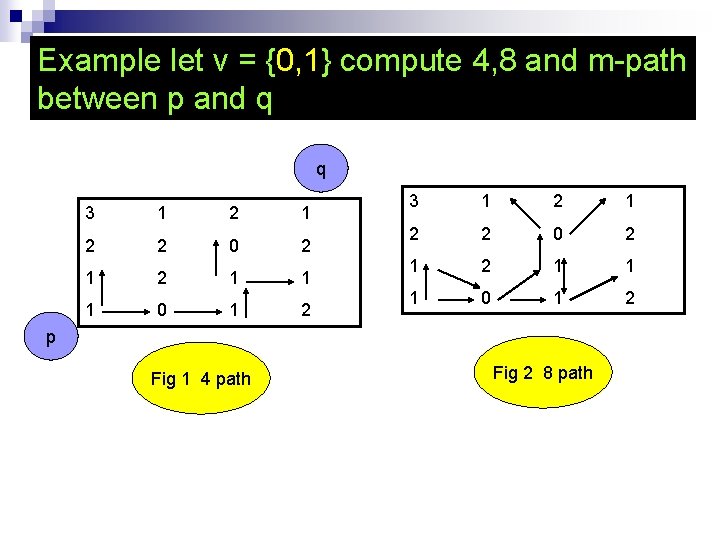
Example let v = {0, 1} compute 4, 8 and m-path between p and q q 3 1 2 1 2 2 0 2 1 2 1 1 1 0 1 2 p Fig 1 4 path Fig 2 8 path

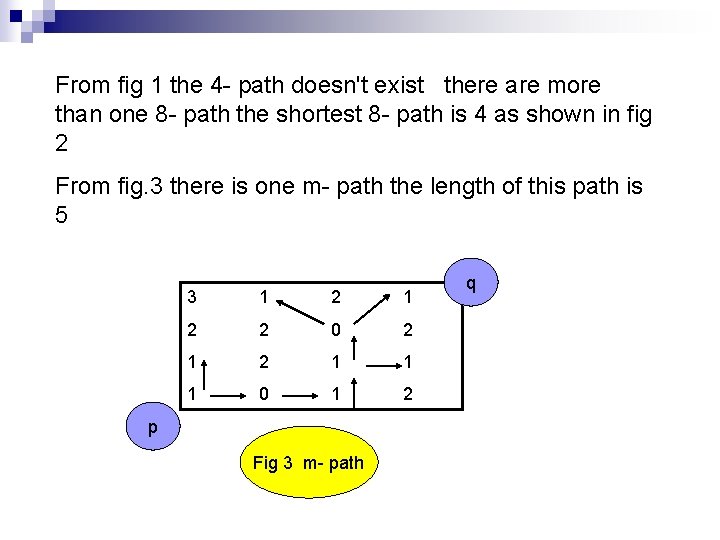
From fig 1 the 4 - path doesn't exist there are more than one 8 - path the shortest 8 - path is 4 as shown in fig 2 From fig. 3 there is one m- path the length of this path is 5 3 1 2 2 0 2 1 1 1 0 1 2 p Fig 3 m- path q

Summary n We have looked at: ¨ What is a digital image? ¨ What is digital image processing? ¨ History of digital image processing ¨ State of the art examples of digital image processing ¨ Key stages in digital image processing