Fundamental relations of traffic flow Transportation Systems Engineering

Fundamental relations of traffic flow Transportation Systems Engineering TVM_IITB_20080807 Fundamental relations of traffic flow

Introduction • Fundamental relations – Time and space mean speed – Fundamental equation (q, k, v) – Fundamental diagrams (q, k, v) TVM_IITB_20080807 Fundamental relations of traffic flow 2

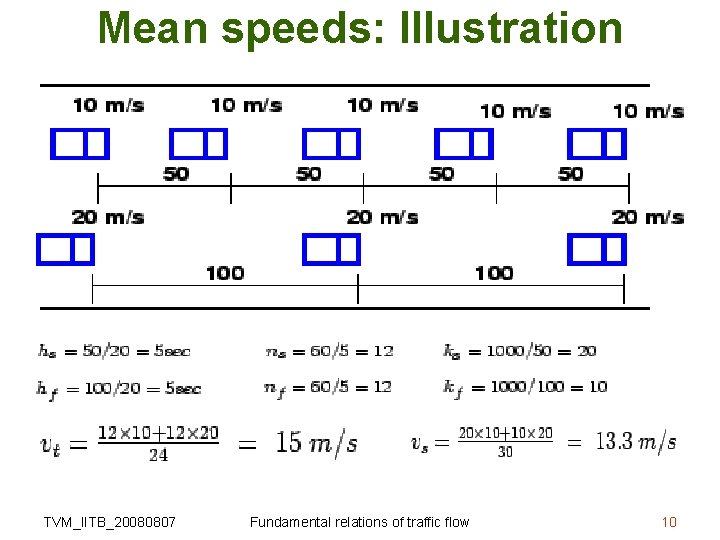
Mean speeds • Time mean speed – average of all vehicles passing a point over a duration of time – It is the simple average of spot speed – Expression for vt – vi spot speed of ith vehicle – n number of observations TVM_IITB_20080807 Fundamental relations of traffic flow 3

Mean speeds • Time mean speed – Speeds may be in the form of frequency table – then vt – qi number of vehicles having speed vi – n number of such speed categories TVM_IITB_20080807 Fundamental relations of traffic flow 4

Mean speeds • Space mean speed – average speed in a stretch at an instant – It also averages the spot speed – But spatial weightage instead of temporal TVM_IITB_20080807 Fundamental relations of traffic flow 5

Mean speeds • Space mean speed - derivation – Consider unit length of a road – let vi is the spot speed of ith vehicle – let ti is the time taken to complete unit distance – ti=1/ vi – If there are n such vehicles, then the average travel time ts is given by TVM_IITB_20080807 Fundamental relations of traffic flow 6

Mean speeds • Space mean speed - derivation – If average travel time is ts then – average speed vs is 1/ts – the harmonic mean of the spot speed – If speeds are in a frequency table TVM_IITB_20080807 Fundamental relations of traffic flow 7

Mean speeds • Space mean speed – If speeds are in a frequency table – then vs – qi number of vehicles having speed vi – n number of such speed categories TVM_IITB_20080807 Fundamental relations of traffic flow 8

Mean speeds • Relation between Vt and Vs – If SMS is vs TMS is vt and the standard deviation of speed is σ – Then – vt > vs sine SD cannot be negative – If all the speed are same, then vs = vt – Derivation (assignment: Refer notes) TVM_IITB_20080807 Fundamental relations of traffic flow 9

Mean speeds: Illustration TVM_IITB_20080807 Fundamental relations of traffic flow 10

Mean speeds • Example 1 – If the spot speeds are 50, 40, 60, 54 and 45, then find the TMS and SMS • Example 2 – The results of a speed study is given in the form of a frequency distribution table. Find the TMS and SMS speed range frequency 2 -5 1 6 -9 4 10 -13 0 14 -17 7 TVM_IITB_20080807 Fundamental relations of traffic flow 11

Fundamental relations • Relationship between q, k, v – Let there be a road with length v km – assume all vehicles are moving with v km/hr – – Number of vehicles counted by an observer at A for one hour be n 1 – By definition, number of vehicles counted in one hour is flow (q) TVM_IITB_20080807 Fundamental relations of traffic flow 12

Fundamental relations • Relationship between q, k, v – n 1=q – Density is the number of vehicles in unit distance – n 2=kv – But, n 1=n 2 • since all vehicle have speed v and the distance is v – Therefore q=kv TVM_IITB_20080807 Fundamental relations of traffic flow 13

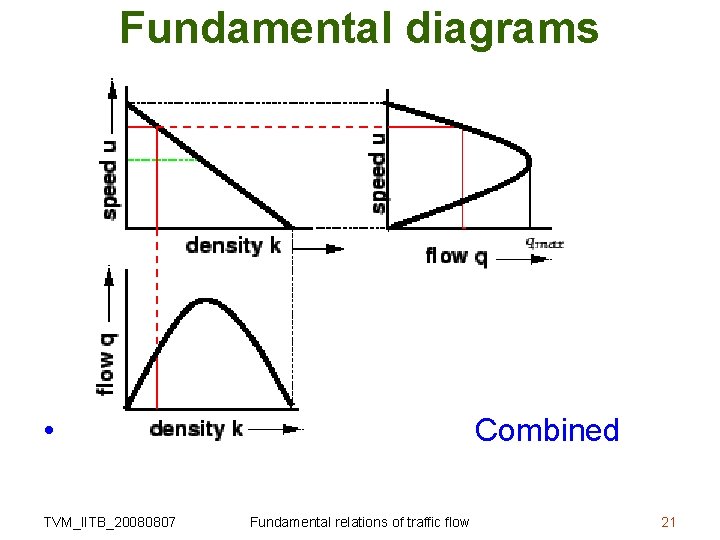
Fundamental diagrams • Follows fundamental relations • Also phenomenological – Flow-density (qk) – Speed-density (kv) – Speed-flow (qv) TVM_IITB_20080807 Fundamental relations of traffic flow 14

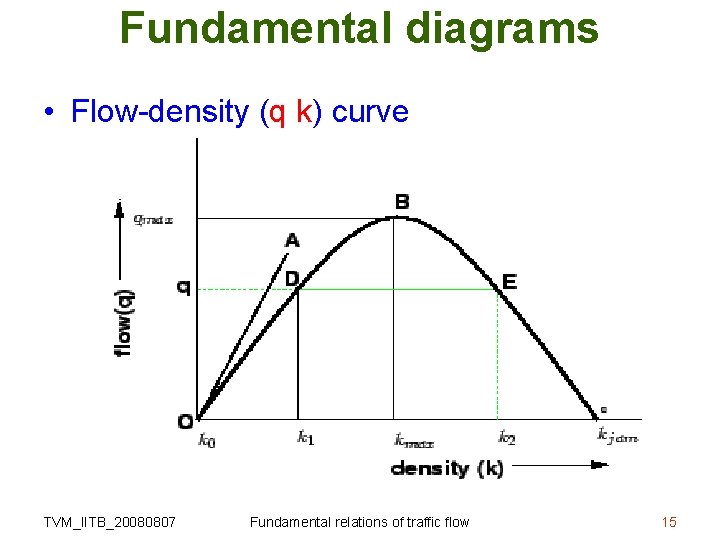
Fundamental diagrams • Flow-density (q k) curve TVM_IITB_20080807 Fundamental relations of traffic flow 15

Fundamental diagrams • Flow-density (q k) curve – The relationship is normally represented by a parabolic curve – At jam density, flow will be zero because the vehicles are not moving. – There will be some density between zero density and jam density, when the flow is maximum. TVM_IITB_20080807 Fundamental relations of traffic flow 16

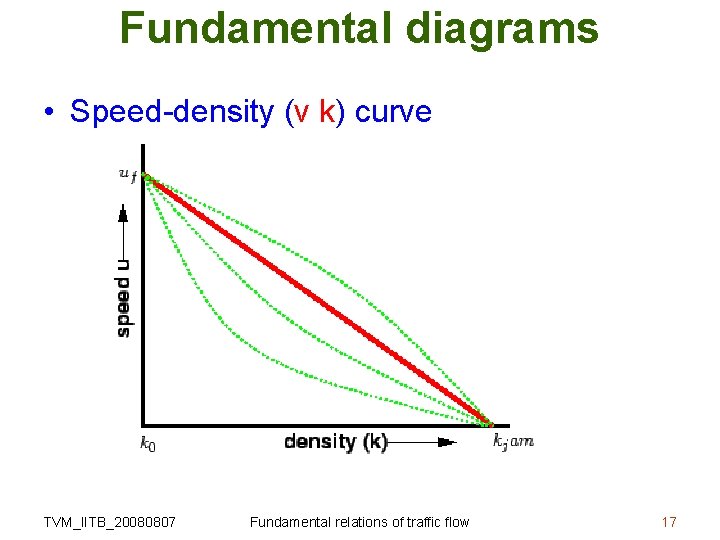
Fundamental diagrams • Speed-density (v k) curve TVM_IITB_20080807 Fundamental relations of traffic flow 17

Fundamental diagrams • Speed-density (v k) curve – Max. speed is free flow speed – Max. density is jam density – At zero density, speed is free flow speed – At jam density, speed becomes zero – Most simple assumption is a linear – Non-linear relationships also possible TVM_IITB_20080807 Fundamental relations of traffic flow 18

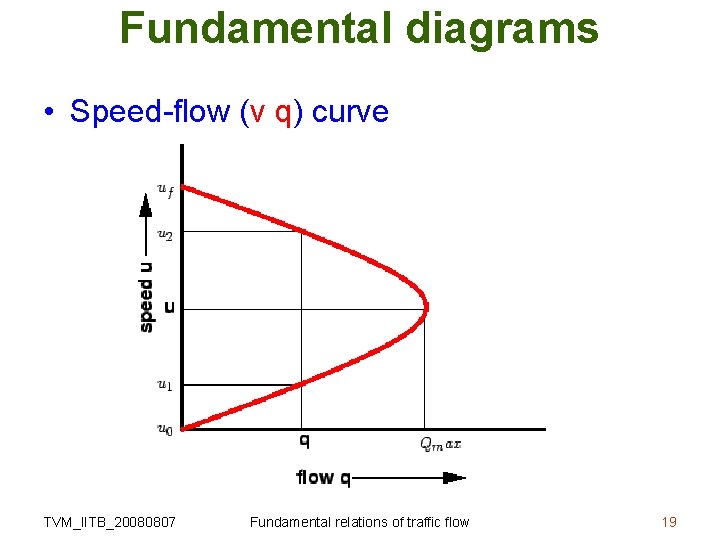
Fundamental diagrams • Speed-flow (v q) curve TVM_IITB_20080807 Fundamental relations of traffic flow 19

Fundamental diagrams • Speed-flow (v q) curve – Flow is zero either because there is no vehicles or there are too many vehicles so that they cannot move – At maximum flow, the speed will be in between zero and free flow speed TVM_IITB_20080807 Fundamental relations of traffic flow 20

Fundamental diagrams • TVM_IITB_20080807 Combined Fundamental relations of traffic flow 21

Relation between Vt and Vs • Derivation – Consider a stream of vehicles with a set of sub-stream flow q 1, q 2, …. . . qi , . . . qn having speed v 1, v 2 , . . . vi, . . . vn. (INCOMEPLETE) – Fundamental relation between flow (q), density (k) and mean speed (vs) – Therefore for any sub-stream qi, the relationship is • Summation of all sub-stream flows is total flow q TVM_IITB_20080807 Fundamental relations of traffic flow 22

Relation between Vt and Vs • Derivation – Consider a stream of vehicles with a set of sub-stream flow q 1, q 2, …. . . qi , . . . qn having speed v 1, v 2 , . . . vi, . . . vn. (INCOMEPLETE) • Fundamental relation between flow (q), density (k) and mean speed (vs) • Therefore for any sub-stream qi, the relationship is • Summation of all sub-stream flows is total flow q TVM_IITB_20080807 Fundamental relations of traffic flow 23

• Space mean speed averages the speed over space. • If ki vehicles have vi speed, then space mean speed is (INCOMEPLETE) • Time mean speed averages the speed over time, • Substituting in TVM_IITB_20080807 Fundamental relations of traffic flow 24

• By adding and subtracting vs and doing algebraic manipulations, vt can be written as, (INCOMEPLETE) • The third term of the equation will be zero because will be zero, since vs is the mean speed of vi. Fundamental relations of traffic flow 25 • The numerator of the second term gives the TVM_IITB_20080807

Thank You tomvmathew@gmail. com TVM_IITB_20080807 Fundamental relations of traffic flow