Fundamental properties Volume flow rate Mass flow rate

Fundamental properties Volume flow rate Mass flow rate In vector fields

Control volume approach (검사체적 방법) A method by which a volume in the flow field is identical and the governing eqns are solved for the flow properties associated with this volume → Eulerian concept Control volume (cv) a volume taken from the flow field space for the evaluation of properties of a fluid in motion Control surface (cs) surface comprising the control volume

Extensive/intensive properties Extensive property – dependent on the system size (mass), denoted as uppercase letters ex) mass (M), momentum (Mv), energey (E) Intensive property – independent on the system size (mass), denoted as lowercase letters ex) unity of M/M(=1), momentum-v, energy per unit mass (e) Amount of extensive property, B in the cv

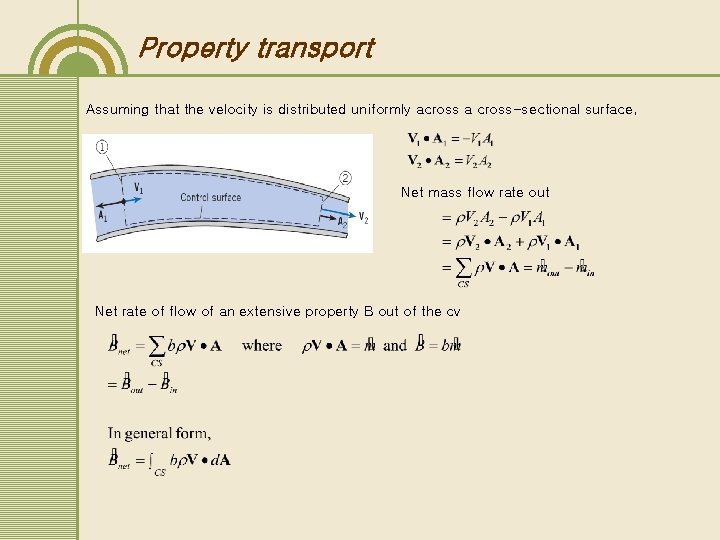
Property transport Assuming that the velocity is distributed uniformly across a cross-sectional surface, Net mass flow rate out Net rate of flow of an extensive property B out of the cv

Reynolds transport theorem transforming the governing eqns for a given mass, the Lagrangian form, into the corresponding eqns for mass passing through a cv in space, the Eulerian form. For the property B, Lagrangian Eulerian

Continuity equation (연속 방정식) The extensive property is the system mass, The corresponding intensive property, Applying the Reynolds transport theorem, From the principle of the conservation of mass,

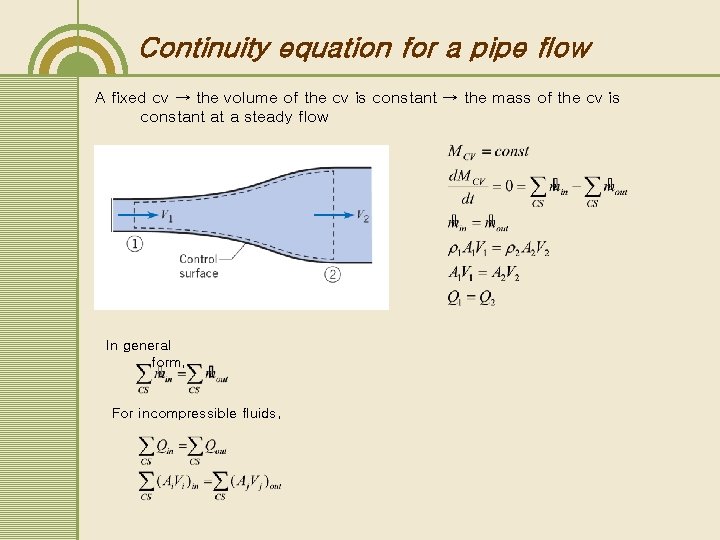
Continuity equation for a pipe flow A fixed cv → the volume of the cv is constant → the mass of the cv is constant at a steady flow In general form, For incompressible fluids,

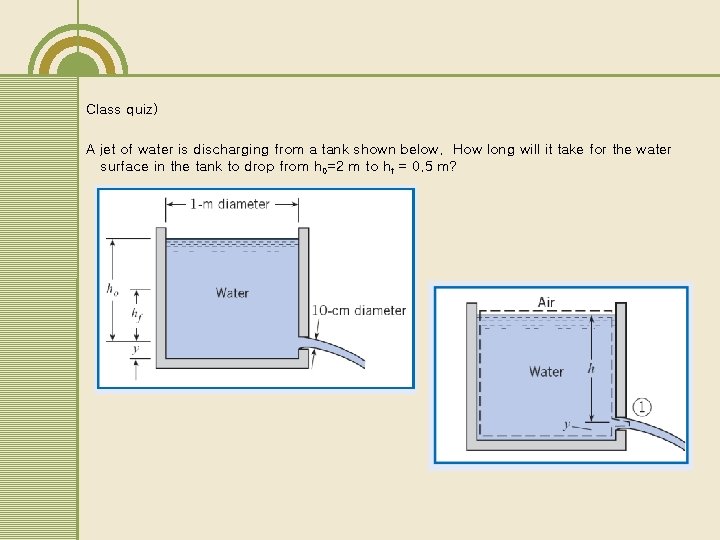
Class quiz) A jet of water is discharging from a tank shown below. How long will it take for the water surface in the tank to drop from h 0=2 m to hf = 0. 5 m?

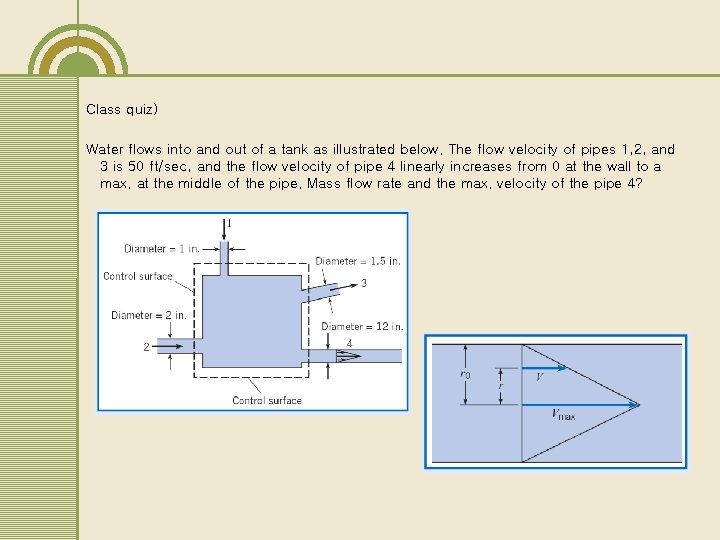
Class quiz) Water flows into and out of a tank as illustrated below. The flow velocity of pipes 1, 2, and 3 is 50 ft/sec, and the flow velocity of pipe 4 linearly increases from 0 at the wall to a max. at the middle of the pipe. Mass flow rate and the max. velocity of the pipe 4?

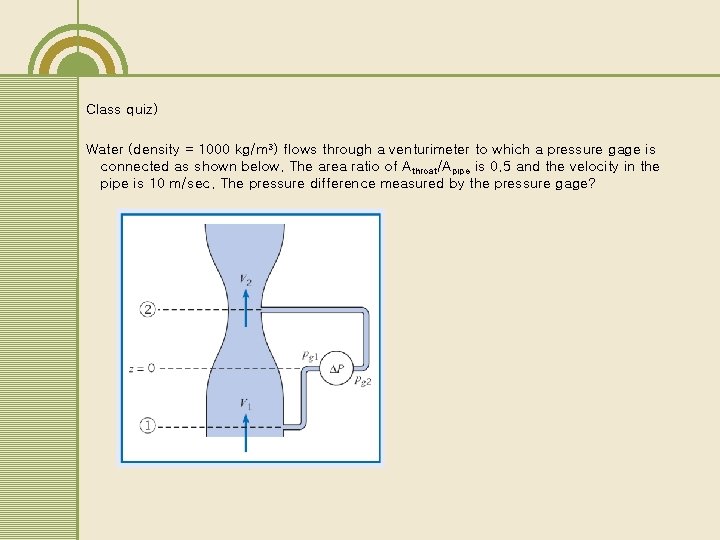
Class quiz) Water (density = 1000 kg/m 3) flows through a venturimeter to which a pressure gage is connected as shown below. The area ratio of Athroat/Apipe is 0. 5 and the velocity in the pipe is 10 m/sec. The pressure difference measured by the pressure gage?

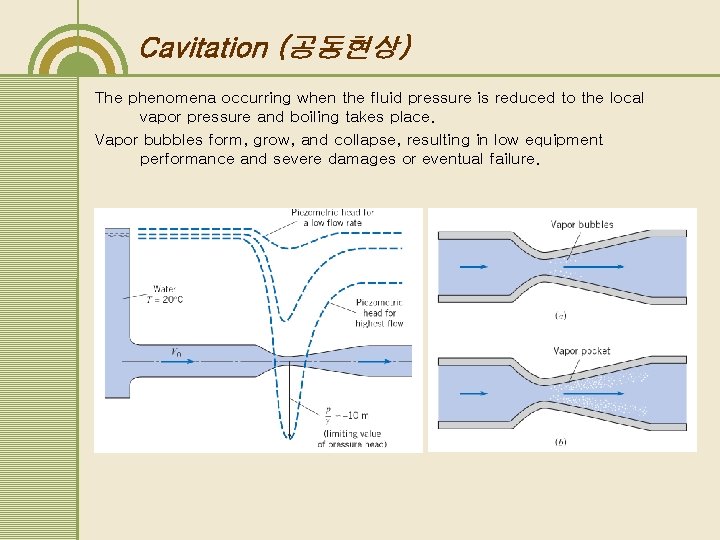
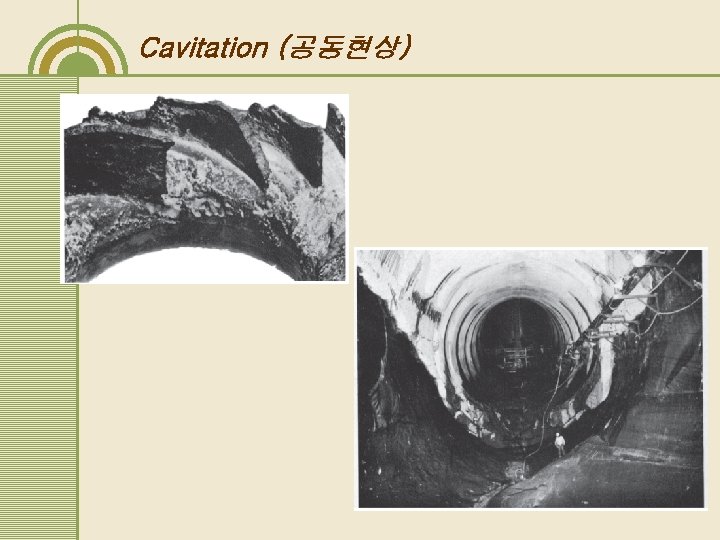
Cavitation (공동현상) The phenomena occurring when the fluid pressure is reduced to the local vapor pressure and boiling takes place. Vapor bubbles form, grow, and collapse, resulting in low equipment performance and severe damages or eventual failure.

Cavitation (공동현상)

Momentum principle (운동량 원리) The momentum equation defines the relationship between velocity and forces applied on a fluid at motion. Useful for analyzing forces, work, and power given to/produced by pipe bends, jets, nozzle, turbojets, turbines, etc. By the Newton’s 2 nd law force and momentum, By the Reynolds transport theorem, Extensive property = momentum of system Intensive property = momentum per unit system mass

What does it mean? The sum of external forces on the cv = the rate of momentum change (momentum accumulation) + the net rate at which momentum flows out of the cv. Note) In many cases (e. g. , steady flow, flow passing a stationary structural part), the momentum accumulation is “ 0”. v is relative to an inertial reference frame (for the momentum out of/into cv). V is fluid velocity relative to the cs at the location where the flow is crossing the cs (for the rate of mass flow out of/into cv, independent of the inertial reference frame).

Vector expression Momentum diagram – Draw a control volume Draw a vector to represent the momentum accumulation term Draw a vector to represent momentum flow at each section where mass crosses the cv. 0

Cartesian coordinates When the velocity v is uniformly distributed across the control surface, X direction: y direction: z direction: Approach for solving problems Problem setup Select a cv and an inertial reference frame Identify governing equations Force analysis Draw a force diagram (body and surface forces) Momentum analysis Draw a momentum diagram Setup a momentum equation

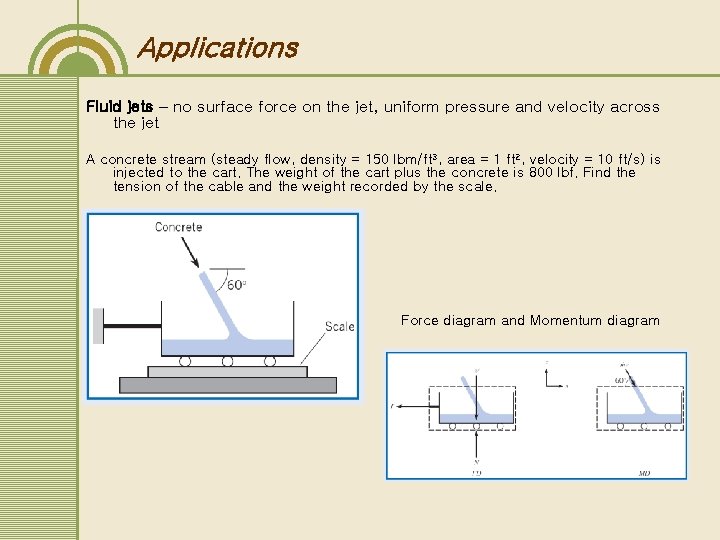
Applications Fluid jets – no surface force on the jet, uniform pressure and velocity across the jet A concrete stream (steady flow, density = 150 lbm/ft 3, area = 1 ft 2, velocity = 10 ft/s) is injected to the cart. The weight of the cart plus the concrete is 800 lbf. Find the tension of the cable and the weight recorded by the scale. Force diagram and Momentum diagram

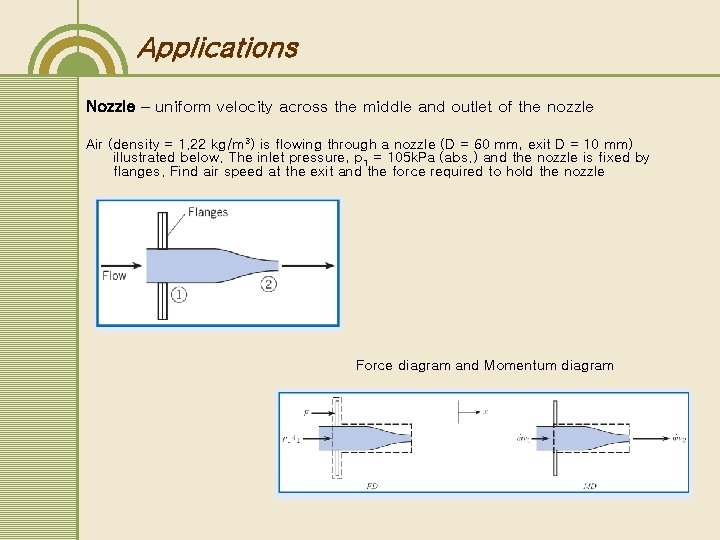
Applications Nozzle – uniform velocity across the middle and outlet of the nozzle Air (density = 1. 22 kg/m 3) is flowing through a nozzle (D = 60 mm, exit D = 10 mm) illustrated below. The inlet pressure, p 1 = 105 k. Pa (abs. ) and the nozzle is fixed by flanges. Find air speed at the exit and the force required to hold the nozzle Force diagram and Momentum diagram

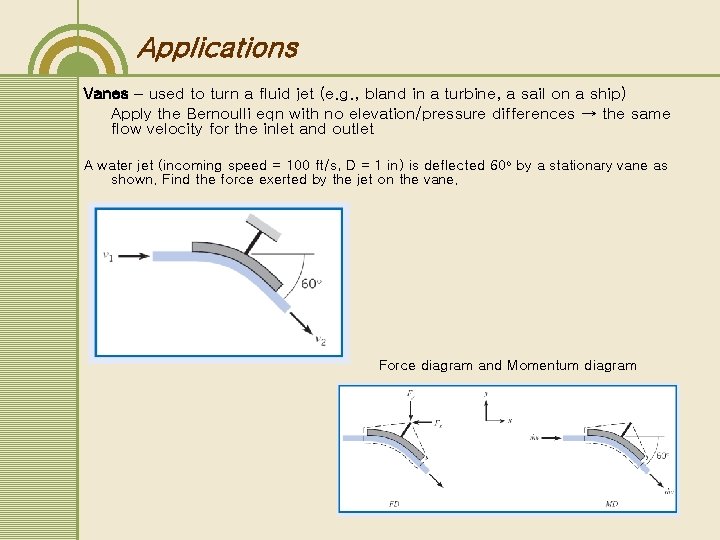
Applications Vanes – used to turn a fluid jet (e. g. , bland in a turbine, a sail on a ship) Apply the Bernoulli eqn with no elevation/pressure differences → the same flow velocity for the inlet and outlet A water jet (incoming speed = 100 ft/s, D = 1 in) is deflected 60 o by a stationary vane as shown. Find the force exerted by the jet on the vane. Force diagram and Momentum diagram

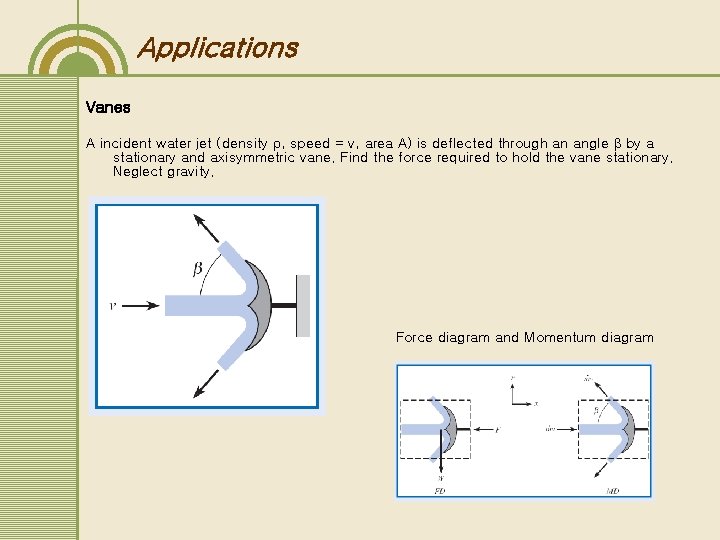
Applications Vanes A incident water jet (density , speed = v, area A) is deflected through an angle by a stationary and axisymmetric vane. Find the force required to hold the vane stationary. Neglect gravity. Force diagram and Momentum diagram

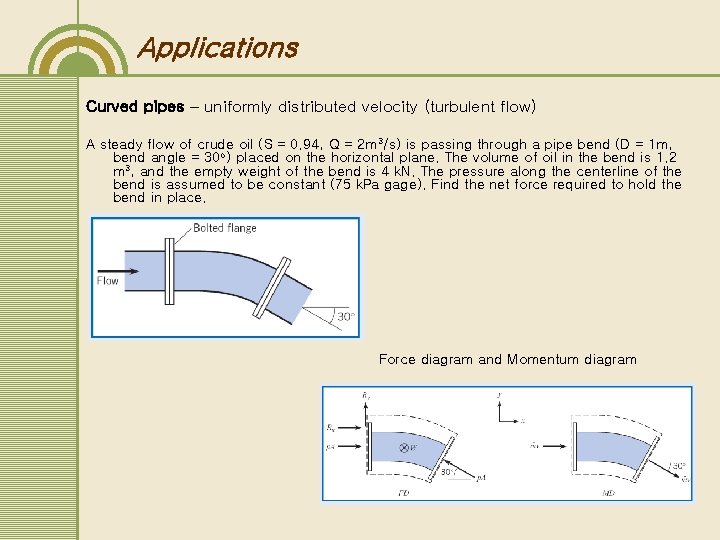
Applications Curved pipes – uniformly distributed velocity (turbulent flow) A steady flow of crude oil (S = 0. 94, Q = 2 m 3/s) is passing through a pipe bend (D = 1 m, bend angle = 30 o) placed on the horizontal plane. The volume of oil in the bend is 1. 2 m 3, and the empty weight of the bend is 4 k. N. The pressure along the centerline of the bend is assumed to be constant (75 k. Pa gage). Find the net force required to hold the bend in place. Force diagram and Momentum diagram

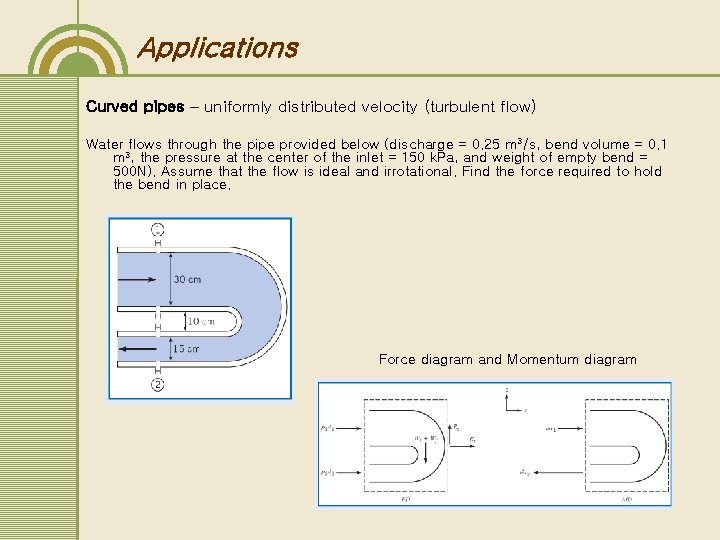
Applications Curved pipes – uniformly distributed velocity (turbulent flow) Water flows through the pipe provided below (discharge = 0. 25 m 3/s, bend volume = 0. 1 m 3, the pressure at the center of the inlet = 150 k. Pa, and weight of empty bend = 500 N). Assume that the flow is ideal and irrotational. Find the force required to hold the bend in place. Force diagram and Momentum diagram

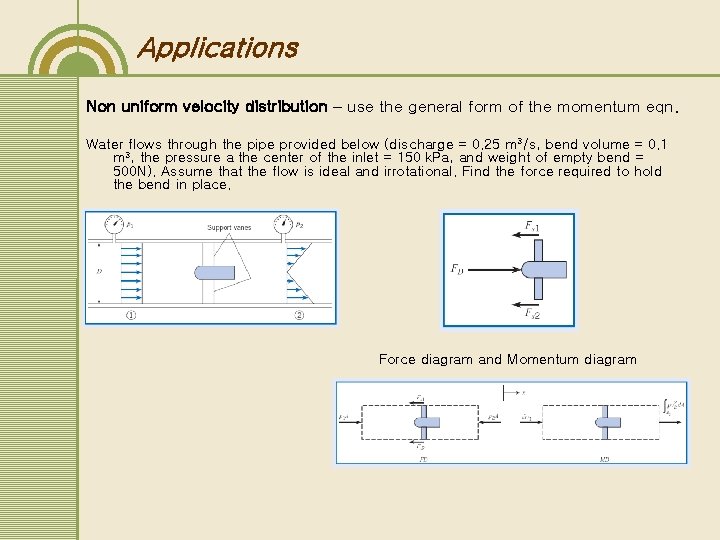
Applications Non uniform velocity distribution – use the general form of the momentum eqn. Water flows through the pipe provided below (discharge = 0. 25 m 3/s, bend volume = 0. 1 m 3, the pressure a the center of the inlet = 150 k. Pa, and weight of empty bend = 500 N). Assume that the flow is ideal and irrotational. Find the force required to hold the bend in place. Force diagram and Momentum diagram

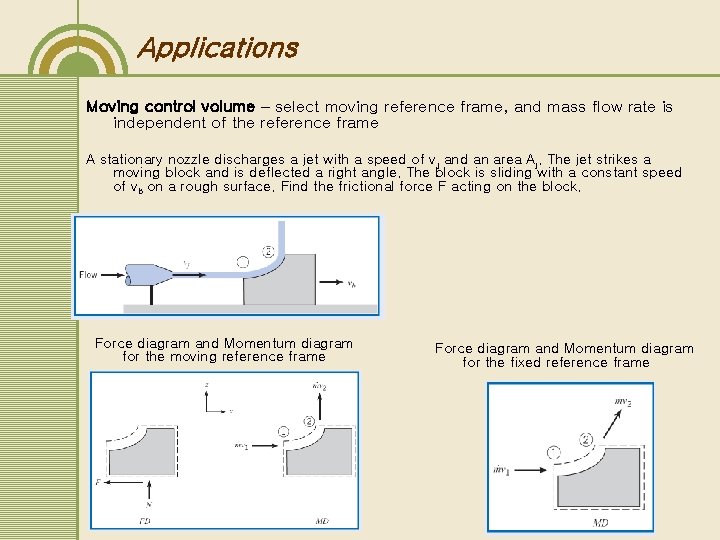
Applications Moving control volume – select moving reference frame, and mass flow rate is independent of the reference frame A stationary nozzle discharges a jet with a speed of vj and an area Aj. The jet strikes a moving block and is deflected a right angle. The block is sliding with a constant speed of vb on a rough surface. Find the frictional force F acting on the block. Force diagram and Momentum diagram for the moving reference frame Force diagram and Momentum diagram for the fixed reference frame

Moment of Momentum equation (운동량 모멘트 방정식) Useful for the analyses of rotating machinery (pumps, turbines, and blowers) By Newton’s 2 nd law for moment (torque) and angular momentum, By the Reynolds transport theorem,

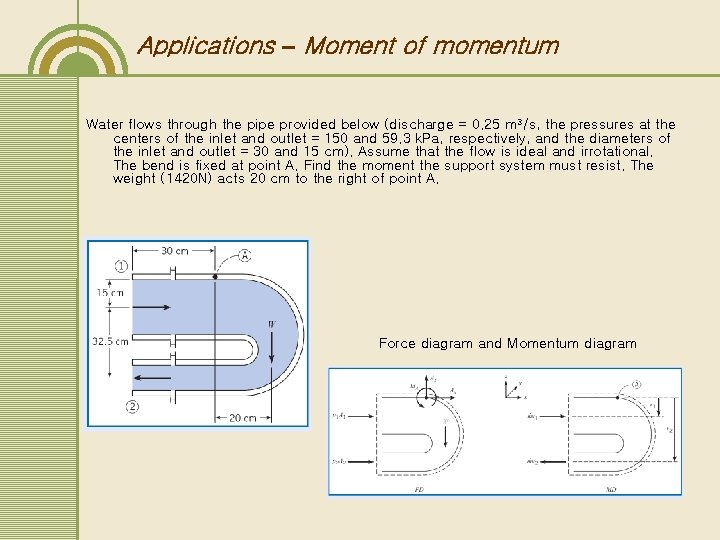
Applications – Moment of momentum Water flows through the pipe provided below (discharge = 0. 25 m 3/s, the pressures at the centers of the inlet and outlet = 150 and 59. 3 k. Pa, respectively, and the diameters of the inlet and outlet = 30 and 15 cm). Assume that the flow is ideal and irrotational. The bend is fixed at point A. Find the moment the support system must resist. The weight (1420 N) acts 20 cm to the right of point A. Force diagram and Momentum diagram

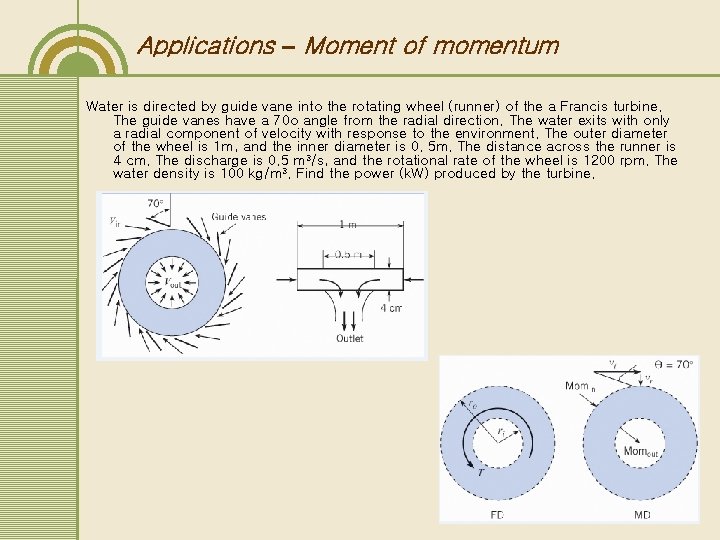
Applications – Moment of momentum Water is directed by guide vane into the rotating wheel (runner) of the a Francis turbine. The guide vanes have a 70 o angle from the radial direction. The water exits with only a radial component of velocity with response to the environment. The outer diameter of the wheel is 1 m, and the inner diameter is 0. 5 m. The distance across the runner is 4 cm. The discharge is 0. 5 m 3/s, and the rotational rate of the wheel is 1200 rpm. The water density is 100 kg/m 3. Find the power (k. W) produced by the turbine.