Fundamental Concept Option prices dont move in a

Fundamental Concept Option prices don’t move in a linear way compared to their underlying stocks and this makes them complex to understand. Using the Greeks we can understand what will happen to options prices when the market changes.

What are the Greeks? The Greeks are values that describe the sensitivity to change in the price of the Option relative to the factors that drive an option’s price. ? ? ?

Price factors and their Greeks �Underlying price relative to the strike Delta �Perceived risks to the option Implied Volatility Vega �Time to expiration Theta

Knowledge is Power (and other clichés) Using the Greeks we can create what-if style analysis that helps us understand the trade. By understanding the Greeks you can change the way your trade works so it better fits your needs.

What are these Greeks? The main Greeks we care about are; • Delta – The change in price of the option relative to a $1 change in the underlying asset price • Vega – The change in the price of the Option relative to a 1% change in the Implied Volatility • Theta – The amount the option price will change over the next one day period as the option gets closer to the expiration date

An Important Second Order Greek �Gamma – The rate of change in Delta relative to the change in the underlying asset price A little more complex, but very handy for understanding trade risks

The Rest of the Greeks - 1 (per Wikipedia) • • Rho, measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate (for the relevant outstanding term). Lambda, omega, or elasticity is the percentage change in option value percentage change in the underlying price, a measure of leverage, sometimes called gearing. Vanna, also referred to as Dvega. Dspot and Ddelta. Dvol, is a second order derivative of the option value, once to the underlying spot price and once to volatility. It is mathematically equivalent to Ddelta. Dvol, the sensitivity of the option delta with respect to change in volatility; or alternatively, the partial of vega with respect to the underlying instrument's price. Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price. Vomma, Volga, Vega Convexity, Vega gamma or d. Tau/d. Vol measures second order sensitivity to volatility. Vomma is the second derivative of the option value with respect to the volatility, or, stated another way, vomma measures the rate of change to vega as volatility changes. With positive vomma, a position will become long vega as implied volatility increases and short vega as it decreases, which can be scalped in a way analogous to long gamma. And an initially vega-neutral, longvomma position can be constructed from ratios of options at different strikes. Vomma is positive for options away from the money, and initially increases with distance from the money (but drops off as vega drops off). (Specifically, vomma is positive where the usual d 1 and d 2 terms are of the same sign, which is true when d 2 < 0 or d 1 > 0. )

The Rest of the Greeks - 2 (per Wikipedia) • • Charm or delta decay, measures the instantaneous rate of change of delta over the passage of time. Charm has also been called Ddelta. Dtime. Charm can be an important Greek to measure/monitor when delta-hedging a position over a weekend. Charm is a second-order derivative of the option value, once to price and once to the passage of time. It is also then the derivative of theta with respect to the underlying's price. The mathematical result of the formula for charm is expressed in delta/year. It is often useful to divide this by the number of days per year to arrive at the delta decay per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, charm itself may change quickly, rendering full day estimates of delta decay inaccurate. Dvega. Dtime, measures the rate of change in the vega with respect to the passage of time. Dvega. Dtime is the second derivative of the value function; once to volatility and once to time. It is common practice to divide the mathematical result of Dvega. Dtime by 100 times the number of days per year to reduce the value to the percentage change in vega per one day. Vera measures the rate of change in rho with respect to volatility. Vera is the second derivative of the value function; once to volatility and once to interest rate. Vera can be used to assess the impact of volatility change on rho-hedging. Color, gamma decay or Dgamma. Dtime measures the rate of change of gamma over the passage of time. Color is a thirdorder derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes. The mathematical result of the formula for color is expressed in gamma/year. It is often useful to divide this by the number of days per year to arrive at the change in gamma per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, color itself may change quickly, rendering full day estimates of gamma change inaccurate.

The Rest of the Greeks - 3 (per Wikipedia) • • • Speed measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma or Dgamma. Dspot. Speed is the third derivative of the value function with respect to the underlying spot price. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio. Ultima measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been referred to as Dvomma. Dvol. ] Ultima is a third-order derivative of the option value to volatility. Zomma measures the rate of change of gamma with respect to changes in volatility. Zomma has also been referred to as Dgamma. Dvol. Zomma is the third derivative of the option value, twice to underlying asset price and once to volatility. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes.

Are these useful? � To us, probably not � All Greeks are estimates and can vary based on the estimation method used � Second order Greeks are estimates based on estimates and can be very imprecise � True Value - If you happen to be in certain bars in Chicago then knowing what these are may win you a free drink in a trivia contest

Is Implied Volatility a Greek? Technically Implied Volatility is not a Greek, it is a measurement of risk and similar to time and underlying price.

The Good Stuff • Delta, Vega and Theta – Extremely important for analyzing and constructing Trades – Should be available on all options trading platforms

Delta is a dollar value that says • “At the current underlying price, if the underlying goes up by $1 the Option Price will change by X” • Delta will be a Positive value between $0 and $1 for Call Options • Delta will be a Negative value between $0 and -$1 for Put options

Notes on Delta • If the Price of the Underlying Asset is At-The-Money then the Delta for the Option is Roughly $. 50 • This is due to the fact there is an equal chance (50/50) the stock will go down as it will go up • Delta is often used as an estimate of the probability that a stock will close above a strike price at expiration – A delta of $. 15 is assumed to mean that there is a 15% chance that the stock will close at or beyond that strike price at the expiration of the Option – Please Note – this is Ok for a rough estimate, but has MANY flaws and can be quite inaccurate • Delta changes with time if the stock price is not equal to the Option Strike Price – If the Option is ITM then Delta will Increase as it approaches Expiration – If the Option is OTM then Delta will Decrease as it gets closer to Expiration

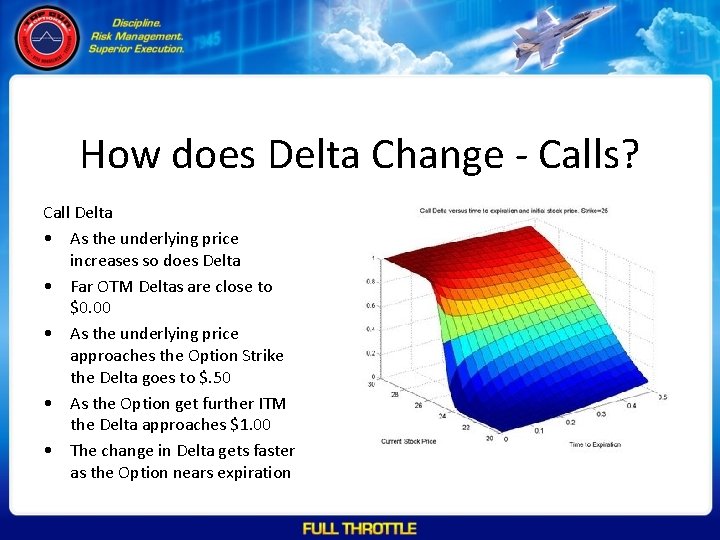
How does Delta Change - Calls? Call Delta • As the underlying price increases so does Delta • Far OTM Deltas are close to $0. 00 • As the underlying price approaches the Option Strike the Delta goes to $. 50 • As the Option get further ITM the Delta approaches $1. 00 • The change in Delta gets faster as the Option nears expiration

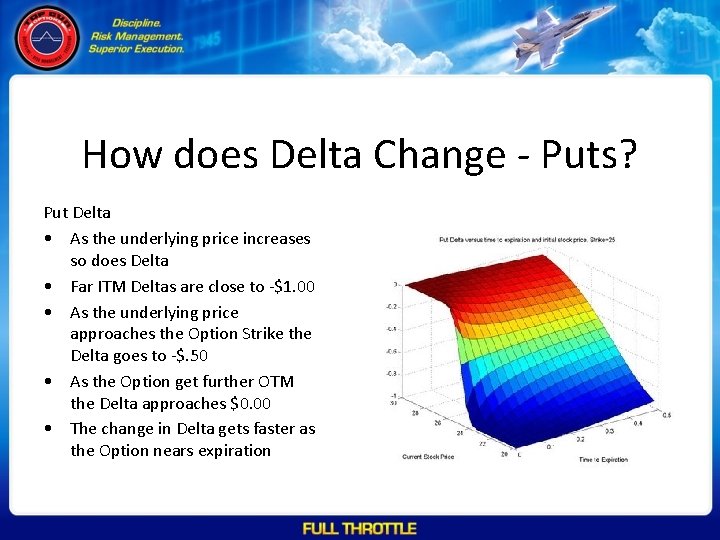
How does Delta Change - Puts? Put Delta • As the underlying price increases so does Delta • Far ITM Deltas are close to -$1. 00 • As the underlying price approaches the Option Strike the Delta goes to -$. 50 • As the Option get further OTM the Delta approaches $0. 00 • The change in Delta gets faster as the Option nears expiration

A few Facts on Delta • The Relationship between Call and Put Delta – The Call Delta(Positive) – the Put Delta(Negative) equals 1 – Based on Put-Call Parity – If you combine a Long Call and a Short Put it equals the movement of the underlying (Delta = 1) – a synthetic stock • Proxy for Probability – Many traders use Delta as a quick estimate of the probability that the option will expire at or beyond that price level – Good for a rough estimate, but it can be misleading

How do we Use Delta • By summing up the Deltas of a position we can see how the trade will react to price movement • By analyzing the Deltas at different price levels we can see where the trade will change price quickly • Delta can also be thought of as the percentage of a lot of stock – A Delta of. 15 = 15% of 100 shares – Using this we can directly hedge other positions

Vega is a dollar value that says • “At this time and at the current level of Implied Volatility, if the Implied Volatility Changes by 1% the Option Price will change by $X” • Vega is Positive for both Puts and Calls – An increase in IV will increase the value of both types of options • Calls and Puts have the same Vega

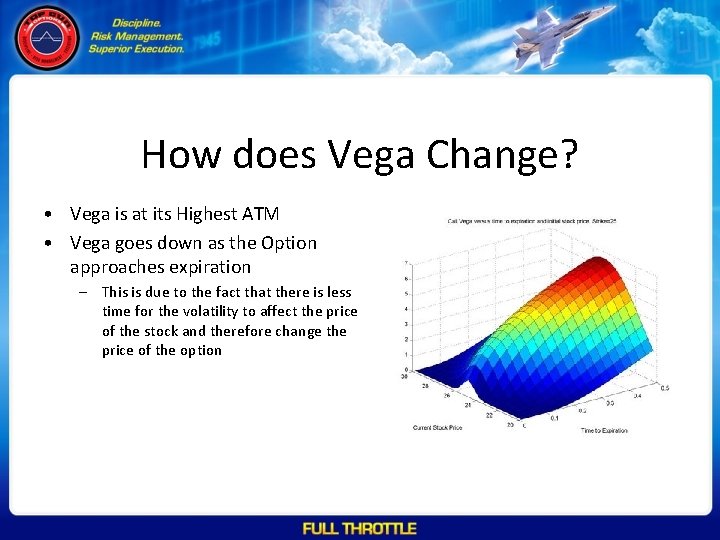
How does Vega Change? • Vega is at its Highest ATM • Vega goes down as the Option approaches expiration – This is due to the fact that there is less time for the volatility to affect the price of the stock and therefore change the price of the option

Facts about Vega • Vega is technically not a Greek letter – A fact that is the basis of many arguments in trader bars in Chicago • As IV increases Vega will increase – This can give you an acceleration effect on Volatility – Inverse is true also

Using Vega - 1 • Vega shows us the effect of predicted or unpredicted changes in volatility on our positions – IV is one of the largest factors in an options price – By using Vega we can model what-if scenarios based on changes in volatility – Using Vega we can craft trades focused specifically on Implied Volatility

Using Vega - 2 • We can sum the total Vega exposure of our portfolio to estimate what will happen if the VIX goes up or down • We can put on trades with offsetting Vega to minimize our exposure to market wide changes in volatility

Theta is a dollar value that says • “Between now and 1 day from now the price of this Call or Put will go down by $X” • Theta is Negative for both Long Puts and Long Calls – As the Options Expiration gets closer Theta becomes a larger negative value – This change accelerates the closer the Option gets to the Expiration – This effect is commonly referred to as Theta Erosion

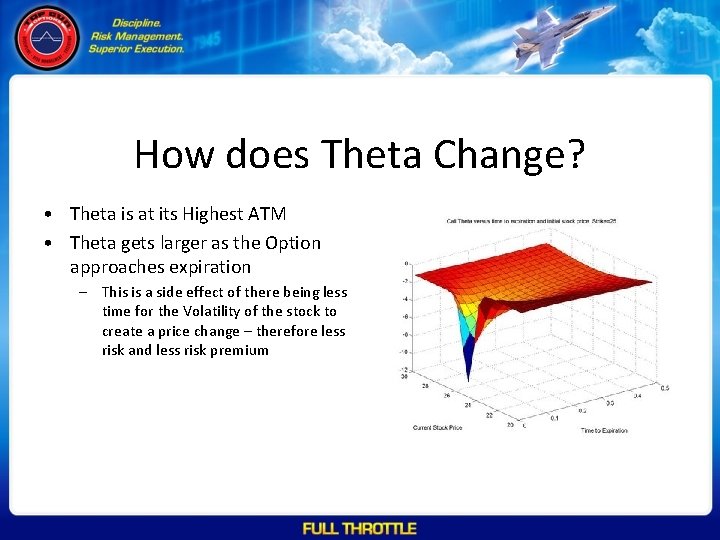
How does Theta Change? • Theta is at its Highest ATM • Theta gets larger as the Option approaches expiration – This is a side effect of there being less time for the Volatility of the stock to create a price change – therefore less risk and less risk premium

Using Theta • By estimating how long we expect to hold a trade we can use theta to determine how much time erosion the trade will experience • This is critical for deciding the direction of the trade (Credit/Debit) and the length of the trades we take • Theta is typically a positive for Credit Trades and a Negative for Debit Trades

Gamma • Gamma is a second derivative of the options price • Gamma tells us how quickly Delta will change based on the change in the underlying asset price • High Gamma is typically beneficial to Debit trades and low Gamma is beneficial to Credit trades • Gamma is a positive number for all Long Positions and Negative number for all short positions

Using Gamma • By analyzing Gamma we can identify Hot Spots – Places where our trades could quickly start to fail. • Gamma can be a good early warning device

Using the Greeks • By summing the Delta, Theta and Vega values across all the Options in our positions we can get a sense of what will happen when specific factors in the market change – What happens if IV goes up? – What happens if the underlying price changes? – What happens if time passes?