Functions Unit PreAlgebra VOCABULARY Relation Domain Range Function

Functions Unit Pre-Algebra

VOCABULARY! Relation: Domain: Range: Function: EXAMPLES! A set of ordered pairs The set of all the input (x) values The set of all the output (y) values A special relation that has exactly ONE output for each input (or exactly ONE y value for each x value) Functions can be represented by: Graphs Tables Input Output Ordered Pairs Function Rules ( , ) y = 2 x + 1 ( , ) y = 4 x ( , ) y = x 2 -1

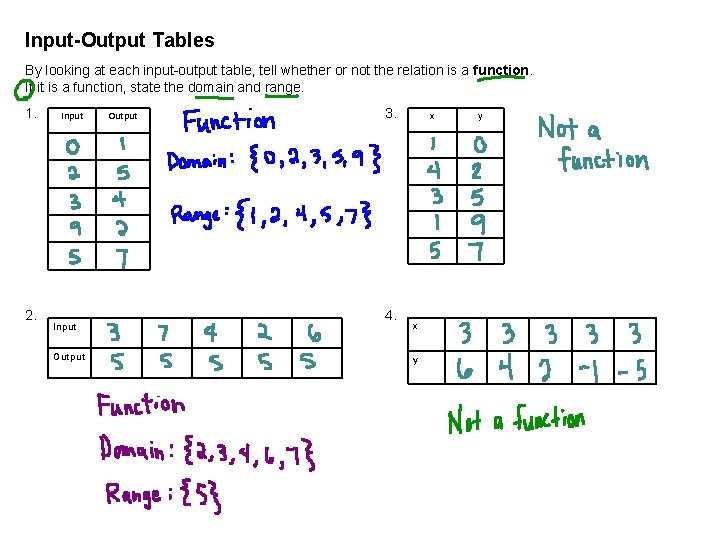
Input-Output Tables By looking at each input-output table, tell whether or not the relation is a function. If it is a function, state the domain and range. 1. 2. Input Output 3. 4. x x y y

Make an input-output table for a function given a specific domain. State the range of the function. 5. 7. 6. 8.

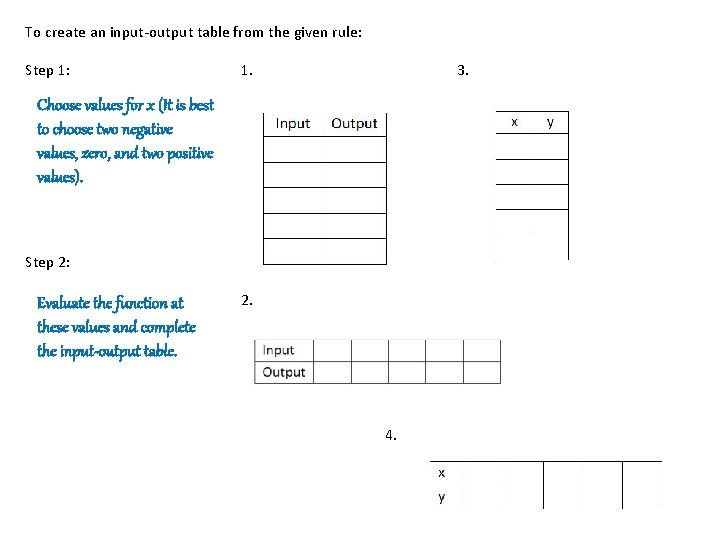
To create an input-output table from the given rule: Step 1: 1. 3. Choose values for x (It is best to choose two negative values, zero, and two positive values). Step 2: Evaluate the function at these values and complete the input-output table. 2. 4.

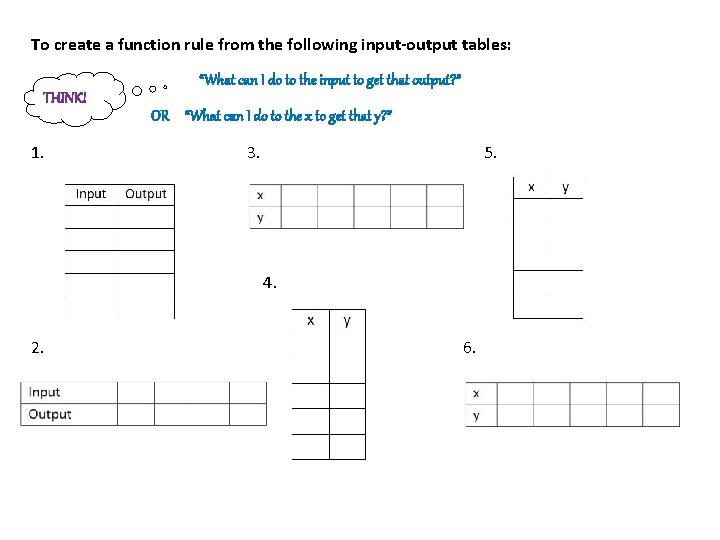
To create a function rule from the following input-output tables: “What can I do to the input to get that output? ” THINK! OR “What can I do to the x to get that y? ” 1. 3. 5. 4. 2. 6.

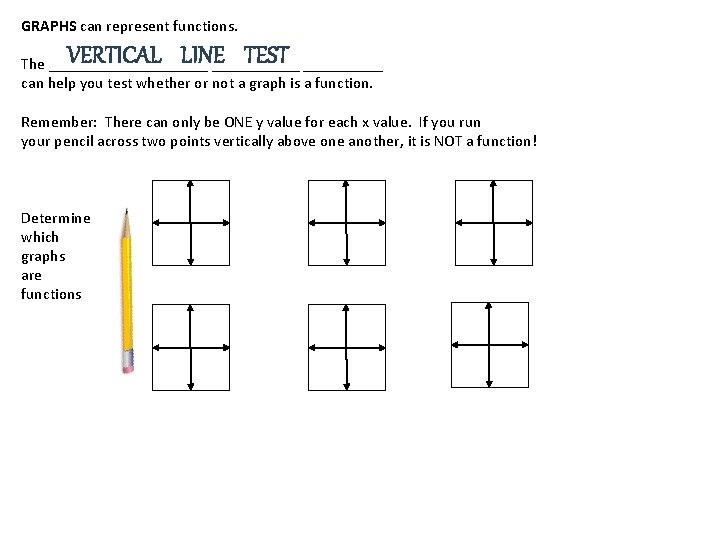
GRAPHS can represent functions. VERTICAL LINE TEST The __________ _____ can help you test whether or not a graph is a function. Remember: There can only be ONE y value for each x value. If you run your pencil across two points vertically above one another, it is NOT a function! Determine which graphs are functions

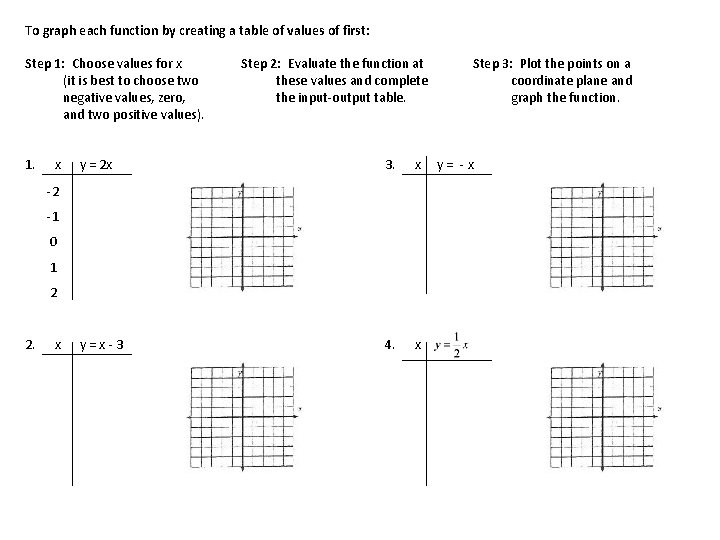
To graph each function by creating a table of values of first: Step 1: Choose values for x (it is best to choose two negative values, zero, and two positive values). 1. x Step 2: Evaluate the function at these values and complete the input-output table. y = 2 x 3. x y=x-3 4. x -2 -1 0 1 2 2. x Step 3: Plot the points on a coordinate plane and graph the function. y= -x

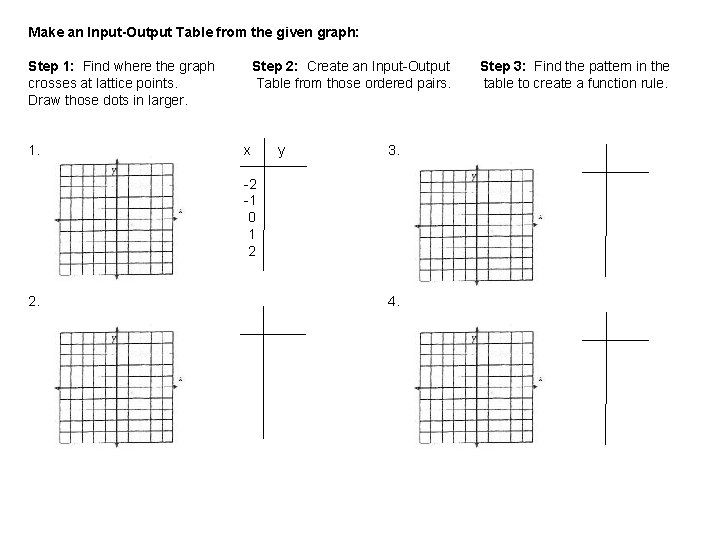
Make an Input-Output Table from the given graph: Step 1: Find where the graph crosses at lattice points. Draw those dots in larger. 1. Step 2: Create an Input-Output Table from those ordered pairs. x y 3. -2 -1 0 1 2 2. 4. Step 3: Find the pattern in the table to create a function rule.