Functions Relations Relation Any set of input that

Functions & Relations

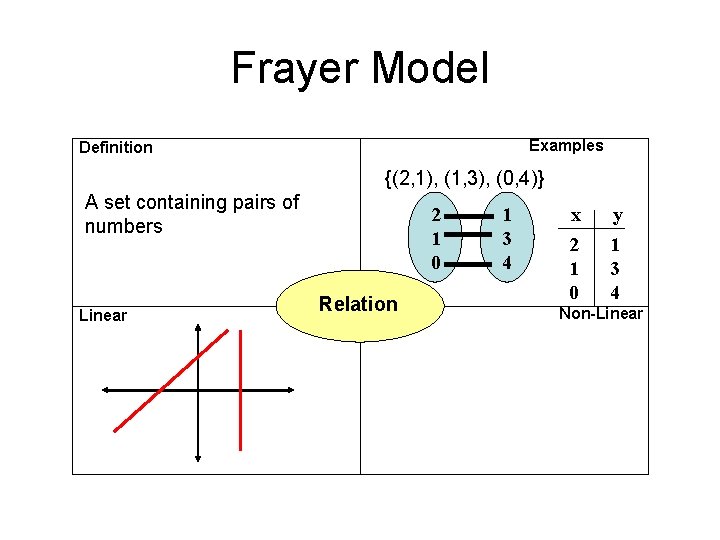
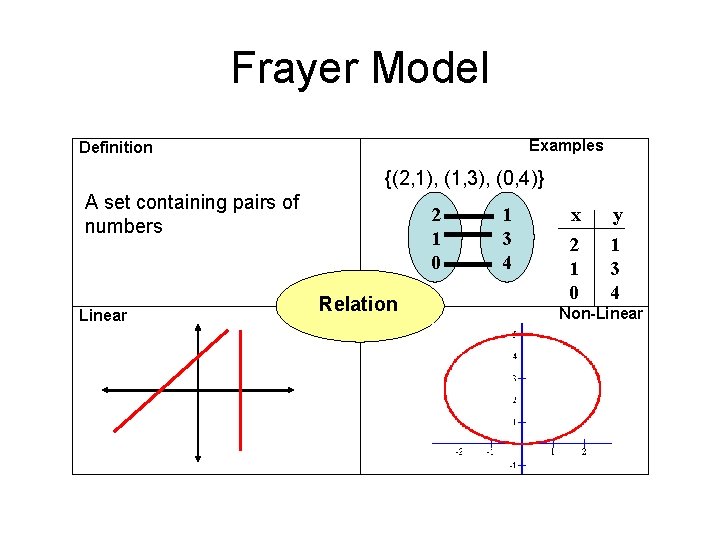
Relation • Any set of input that has an output

Frayer Model Examples Definition Linear Relation Non-Linear

Frayer Model Examples Definition Linear Relation Non-Linear

Frayer Model Examples Definition A set containing pairs of numbers Linear Relation Non-Linear

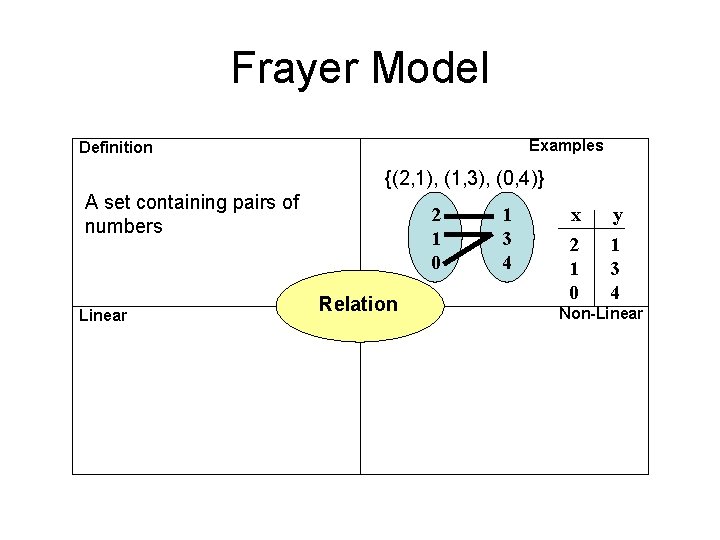
Frayer Model Examples Definition {(2, 1), (1, 3), (0, 4)} A set containing pairs of numbers Linear 2 1 0 Relation 1 3 4 x 2 1 0 y 1 3 4 Non-Linear

Frayer Model Examples Definition {(2, 1), (1, 3), (0, 4)} A set containing pairs of numbers Linear 2 1 0 Relation 1 3 4 x 2 1 0 y 1 3 4 Non-Linear

Frayer Model Examples Definition {(2, 1), (1, 3), (0, 4)} A set containing pairs of numbers Linear 2 1 0 Relation 1 3 4 x 2 1 0 y 1 3 4 Non-Linear

Domain • x – coordinates • Input • Independent variable

Range • y – coordinates • Output • Dependent variable

When listing the domain and range, • Put in order from least to greatest • Only list repeats once

Example Write the domain and range for the following relation. {(2, 6), (-4, -8), (-3, 6), (0, -4)}

You Try 1) Write the domain and range for the following relation. {(-5, 2), (3, -1), (3, 2), (1, 7)}

You Try What are the domain and range?

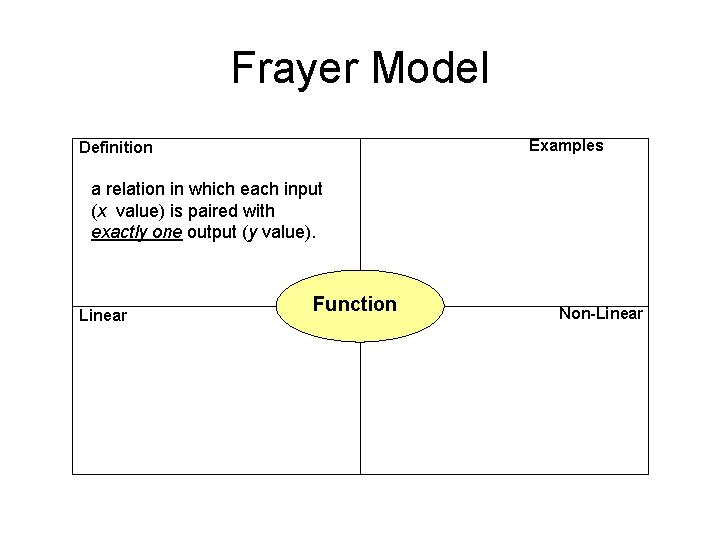
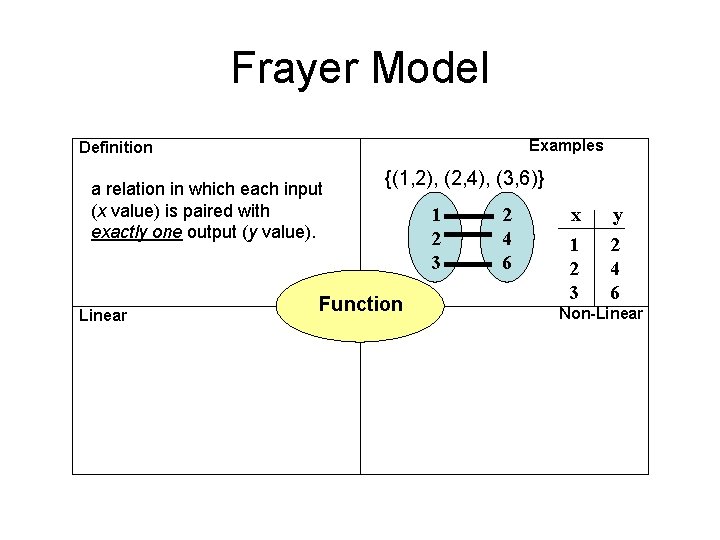
Function • A relation such that every single input has exactly ONE output • Each element from the domain is paired with one and only one element from the range

How do we describe FUNCTIONS ?

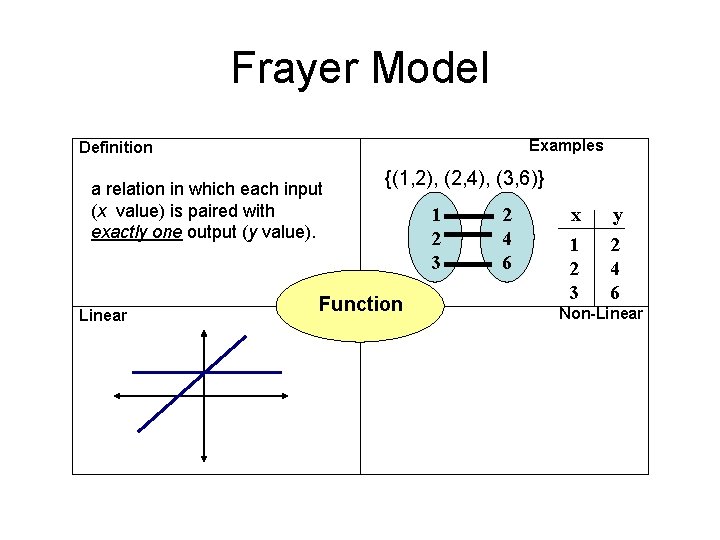
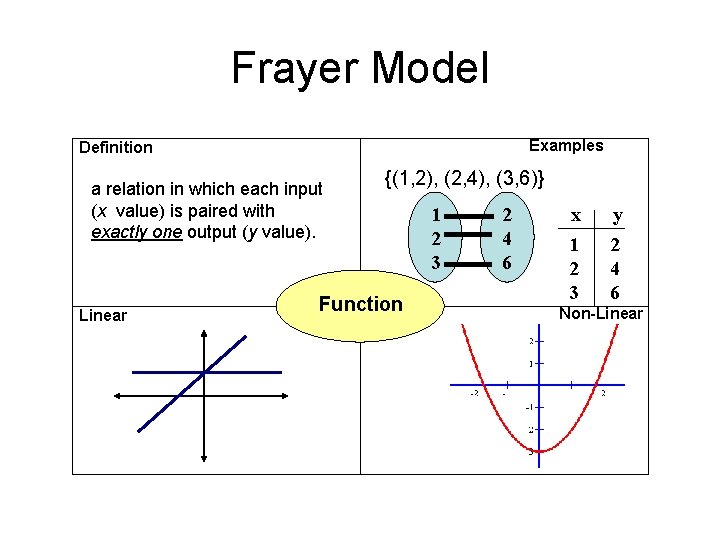
Frayer Model Examples Definition a relation in which each input (x value) is paired with exactly one output (y value). Linear Function Non-Linear

Frayer Model Examples Definition a relation in which each input (x value) is paired with exactly one output (y value). Linear {(1, 2), (2, 4), (3, 6)} Function 1 2 3 2 4 6 x 1 2 3 y 2 4 6 Non-Linear

Frayer Model Examples Definition a relation in which each input (x value) is paired with exactly one output (y value). Linear {(1, 2), (2, 4), (3, 6)} Function 1 2 3 2 4 6 x 1 2 3 y 2 4 6 Non-Linear

Frayer Model Examples Definition a relation in which each input (x value) is paired with exactly one output (y value). Linear {(1, 2), (2, 4), (3, 6)} Function 1 2 3 2 4 6 x 1 2 3 y 2 4 6 Non-Linear

Very Important!!! All functions are relations but not all relations are functions.

How do I know it’s a function? • Look at the input and output table – Each input must have exactly one output. (Domains CANNOT repeat!!!) • Look at the Graph – The Vertical Line test: NO vertical line can pass through two or more points on the graph

Is this relation a function? {(1, 3), (2, 3), (3, 3)} 1. Yes 2. No Answer Now

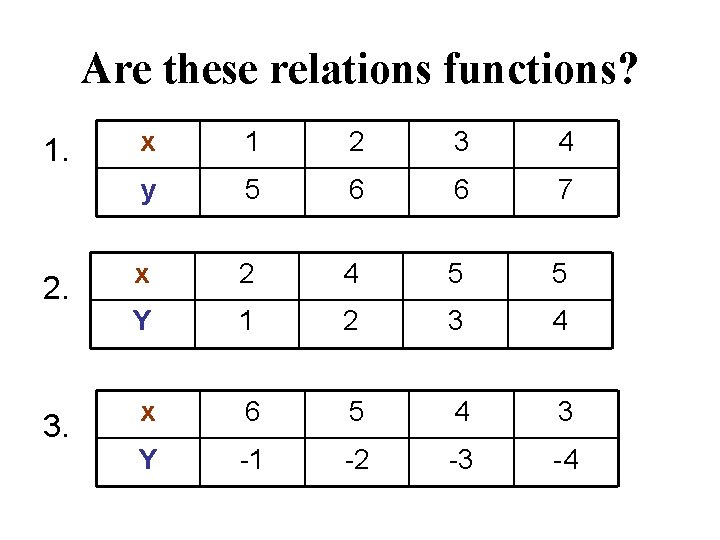
Are these relations functions? 1. (1, 2), (3, 4), (1, 5), (2, 6) 2. (6, 9), (7, 10), (8, 11), (8, – 11) 3. (– 1, – 5), (– 2, – 7), (0, 3), (1, – 5) 4. (2, 4), (3, 5), (2, -4), (3, – 5)

Are these relations functions? 1. 2. 3. x 1 2 3 4 y 5 6 6 7 x 2 4 5 5 Y 1 2 3 4 x 6 5 4 3 Y -1 -2 -3 -4

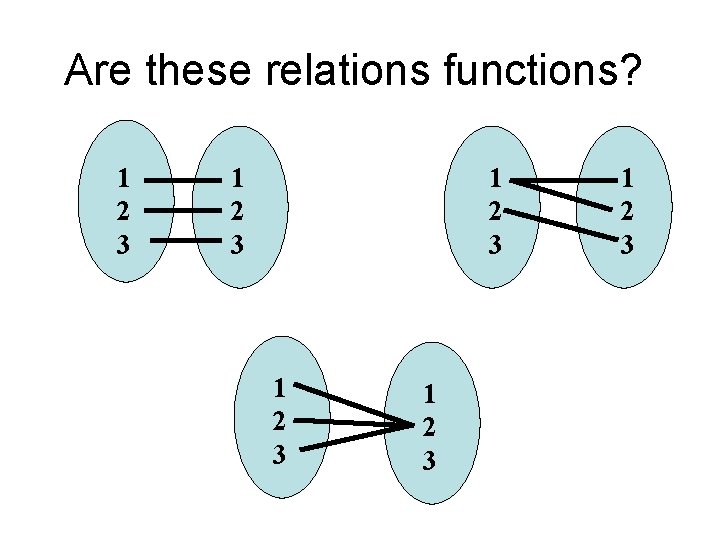
Are these relations functions? 1 2 3 1 2 3

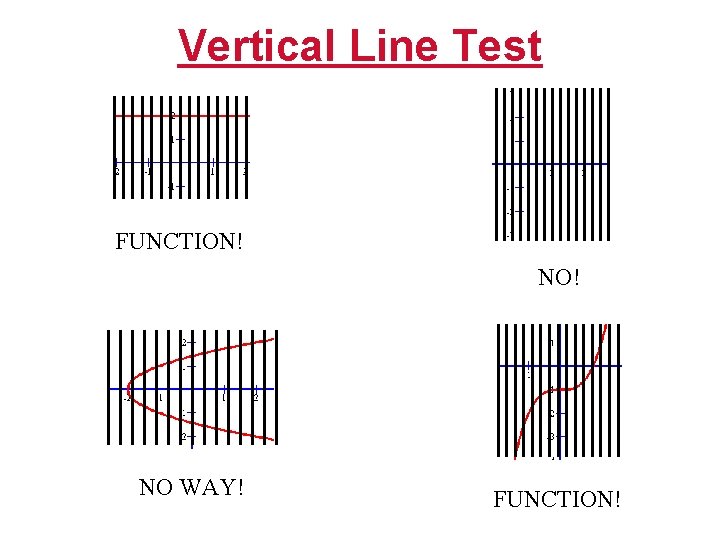
Vertical Line Test (pencil test) If any vertical line passes through more than one point of the graph, then that relation is not a function. Are these functions? FUNCTION! NOPE!

Vertical Line Test FUNCTION! NO WAY! FUNCTION!

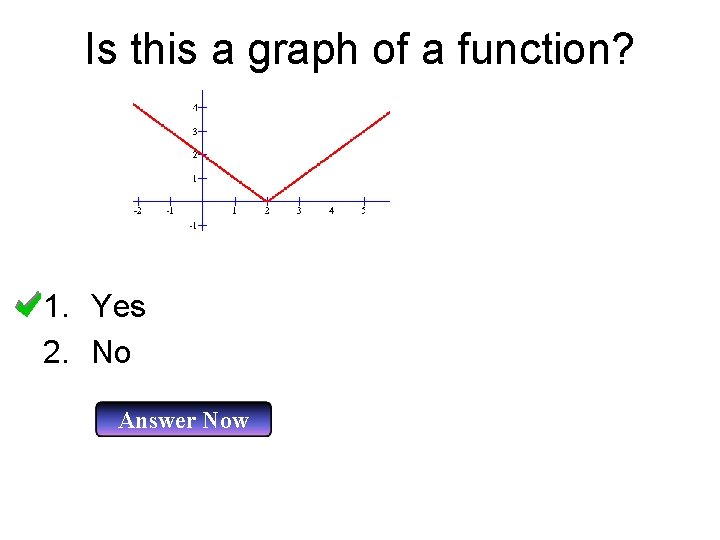
Is this a graph of a function? 1. Yes 2. No Answer Now

An Equation is not a Function if… 1. the “y” variable is raised to an EVEN power; 2. x = any number; x = 5 and x = -9 these are vertical lines.

Are these functions? 1. 2. 3. 4. 5. 6. y=x 2 x+y 4=5 y=x+3 y+6=x 3 x=3 y 2=x 2+4 1. 2. 3. 4. 5. 6. Yes No, y is raised to an even power! Yes No, because the line is vertical! No, y is raised to an even power!

Tell Your Neighbor • How do you know if a relation is a function?

Wednesday: Warm Up Is this relation a function? Explain how you know. {(3, 4), (0, 7), (3, -4), (2, 5)} Vocab Warm-Up Page 465

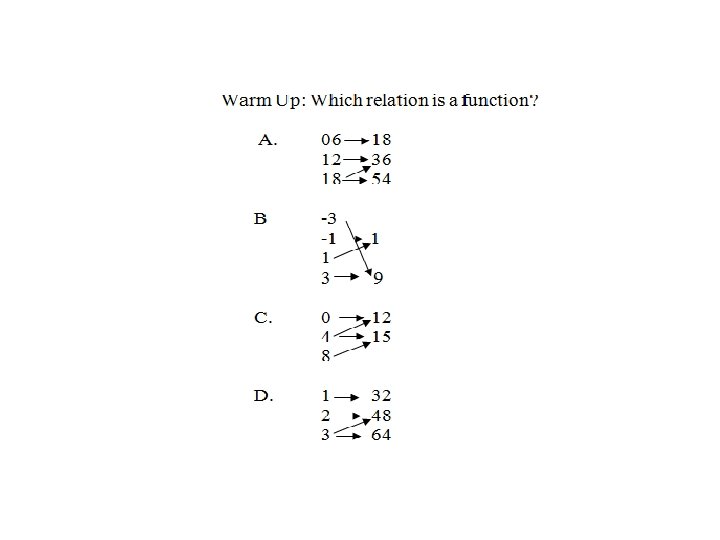
Tuesday Warm Up •

Thursday Warm-Up • Create a table with two columns labeled “Relation and Function” and “Relation Only” • Give examples of each in the following forms: ordered pairs table mapping graph

Test Your Neighbor Make a list of coordinate pairs. Ask your neighbor if the relation is a function.

Success Starter for 1/9/17 Error Analysis-Functions • When asked whether the relation {(-4, 16), (-2, 4), (0, 0), (2, 4)} is a function, Zion stated that the relation is not a function because 4 appears twice. What error did Zion make? How would you explain to the student why this relation is a function? Also, write the domain and range.

Lesson Review Write the definition of the following vocabulary terms: Domain Range Relation Function

Make a mapping diagram of a relation. Ask your neighbor if the relation is a function.

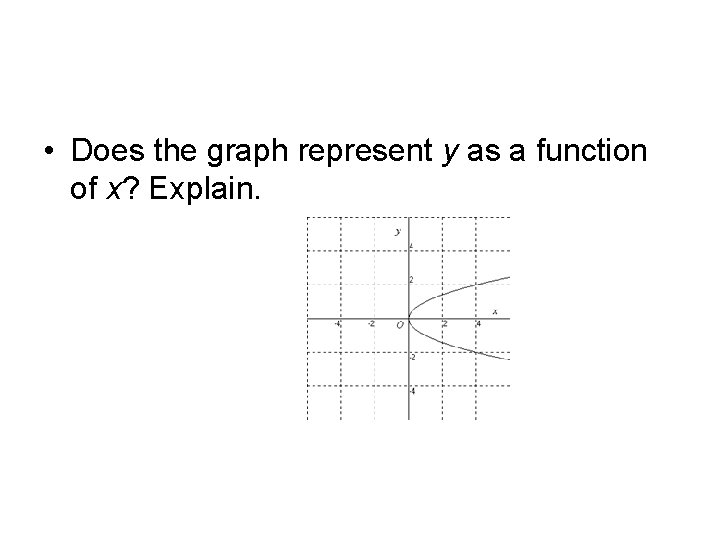
• Does the graph represent y as a function of x? Explain.

Warm Up •