Functions of random variables Sometimes what we can

Functions of random variables • Sometimes what we can measure is not what we are interested in! • Example: mass of binary-star system: • We want M but can only measure V and P. Y • Must conserve probability: f(Y) f(X) X

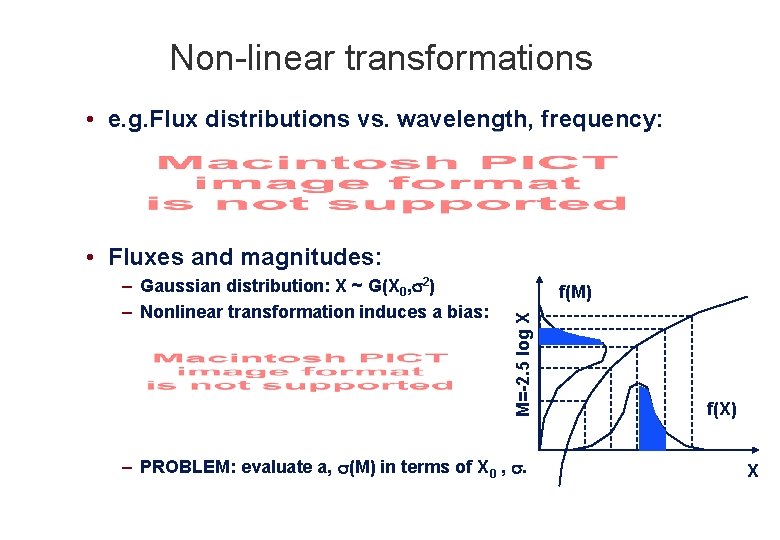
Non-linear transformations • e. g. Flux distributions vs. wavelength, frequency: • Fluxes and magnitudes: f(M) M=-2. 5 log X – Gaussian distribution: X ~ G(X 0, 2) – Nonlinear transformation induces a bias: – PROBLEM: evaluate a, (M) in terms of X 0 , . f(X) X

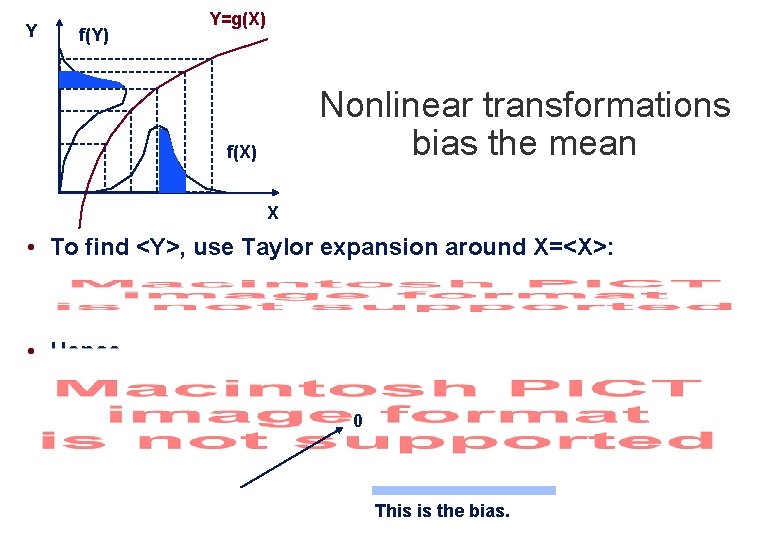
Y f(Y) Y=g(X) Nonlinear transformations bias the mean f(X) X • To find <Y>, use Taylor expansion around X=<X>: • Hence 0 This is the bias.

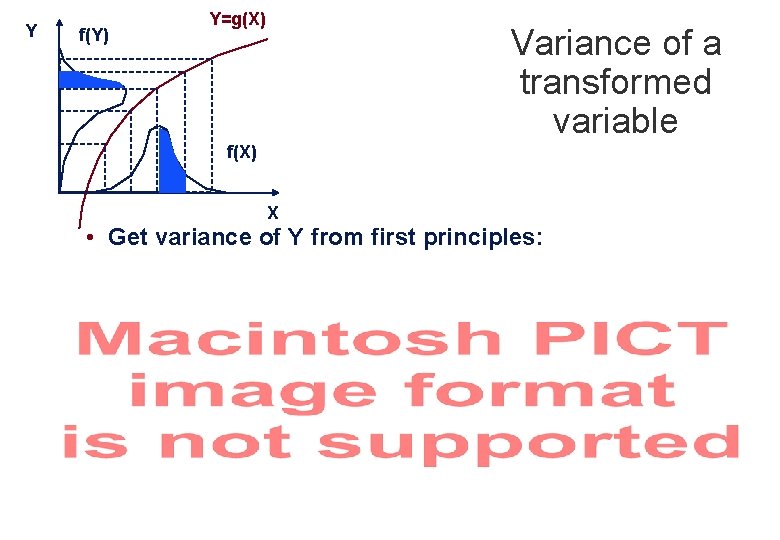
Y f(Y) Y=g(X) Variance of a transformed variable f(X) X • Get variance of Y from first principles:

What is a statistic? • Anything you measure or compute from the data. • Any function of the data. • Because the data “jiggle”, every satistic also “jiggles”. • Example: the mean value of a sample of N data points is a statistic: • It has a definite value for a particular dataset, but it also “jiggles” with the ensemble of datasets to trace out its own PDF. • NB:

Sample mean and variance - 1 • Sample mean: • The distribution of sample means has a mean: • . . . and a variance: if the Xi are independent

Sample mean and variance - 2 • If the Xi are all drawn from a single parent distribution with mean <X> and variance 2, then: • And:

Other unbiased statistics • Sample median (half points above, half below) • (Xmax + Xmin) / 2 • Any single point Xi chosen at random from sequence • Weighted average:

Inverse variance weighting is best! • Let’s evaluate the variance of the weighted average for some weighting function wi: • The variance of the weighted average is minimised when: • Let’s verify this -- it’s important!

Choosing the best weighting function • To minimise the variance of the weighted average, set:

Using optimal weights • Good principles for constructing statistics: – Unbiased -> no systematic error – Minimum variance -> smallest possible statistical error • Optimally (inverse-variance) weighted average: • Is unbiased, since: • And has minimum variance: