Functions of a Random Variable Functions of a

Functions of a Random Variable

Functions of a Random Variable X: g(X): § § a r. v defined on the model a function of the variable x, Is Y necessarily a r. v? If so what is its PDF pdf

Functions of a Random Variable § If X is a r. v, so is Y, and for every Borel set B, § With , In particular § To obtain the distribution function of Y, we must determine the Borel set on the x-axis such that for every given y, and the probability of that set.

Example: § For and hence And We conclude:

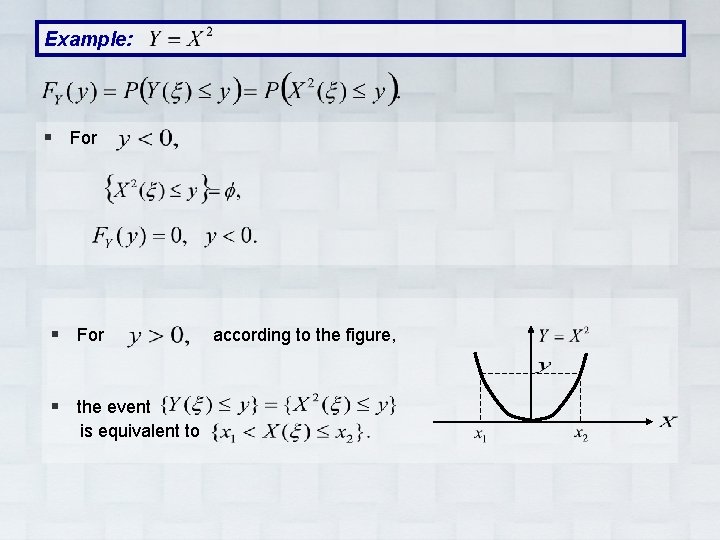
Example: § For § the event is equivalent to according to the figure,

Example: § If - continued represents an even function,

Example: § If - continued so that § We obtain the p. d. f of to be § which represents a Chi-square r. v with n = 1, since § Thus, if X is a Gaussian r. v with then Chi-square r. v with one degree of freedom (n = 1). represents a

Example § For: § We have § For we have and so that

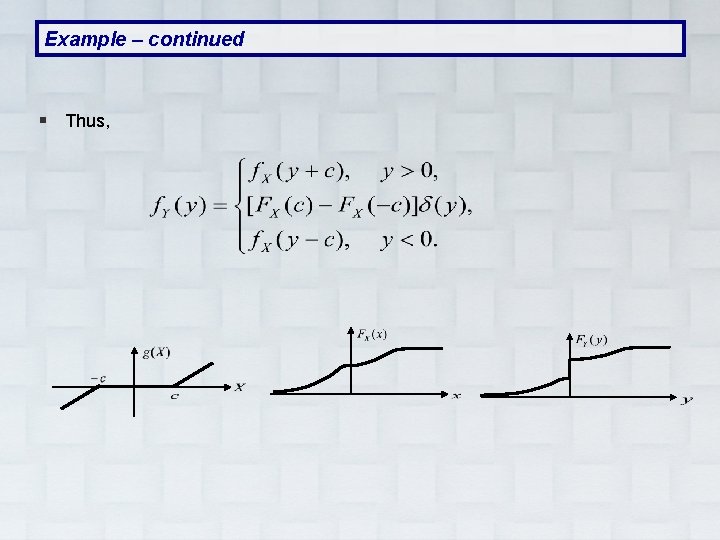
Example – continued § Thus,

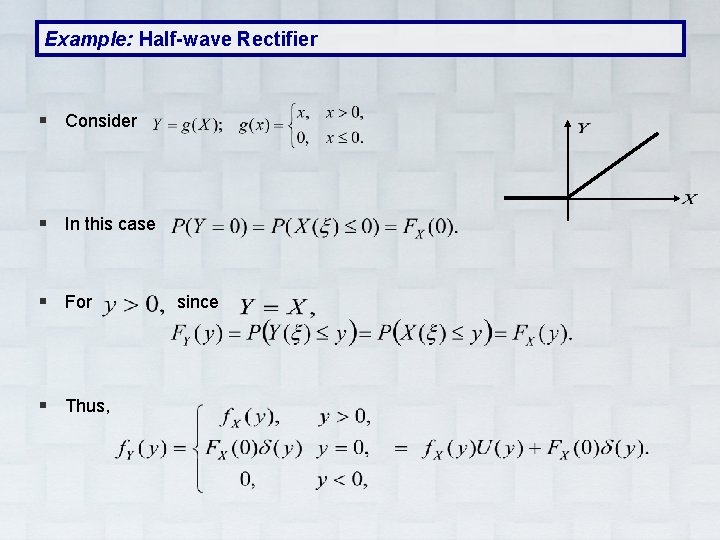
Example: Half-wave Rectifier § Consider § In this case § For § Thus, since

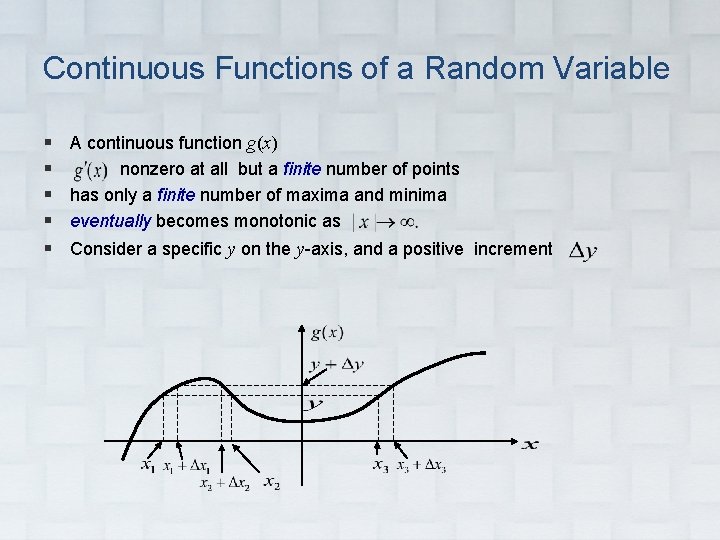
Continuous Functions of a Random Variable § § § A continuous function g(x) nonzero at all but a finite number of points has only a finite number of maxima and minima eventually becomes monotonic as Consider a specific y on the y-axis, and a positive increment

Continuous Functions of a Random Variable § § For where has three solutions is of continuous type, when § X could be in any one of three disjoint intervals: So,

Continuous Functions of a Random Variable § For small § Here, we get and so § As § If the solutions are all in terms of y, the right side is only a function of y.

Example Revisited § For all § and for . § Moreover § and using , which agrees with previous solution.

Example: § Find § Here for every y, § and substituting this into is the only solution, and , we obtain

Example § Suppose and Determine § X has zero probability of falling outside the interval § § has zero probability of falling outside this interval. § For any solutions the equation where § using the symmetry we also get § so that has an infinite number of is the principal solution. etc. Further,

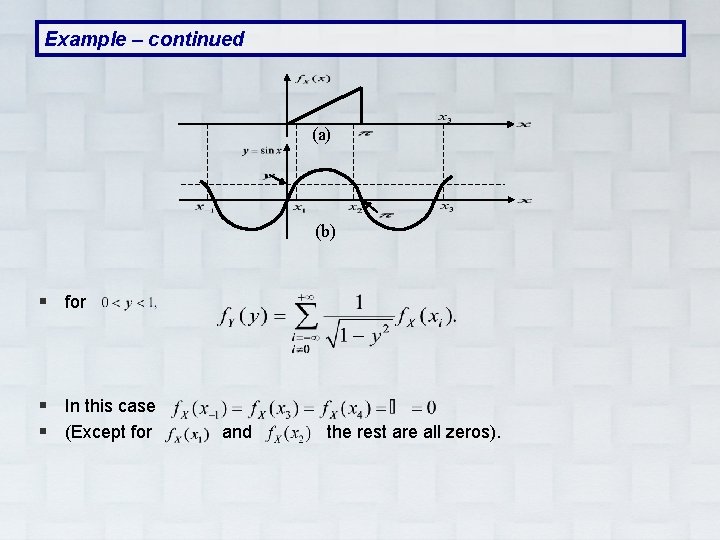
Example – continued (a) (b) § for § In this case § (Except for and the rest are all zeros).

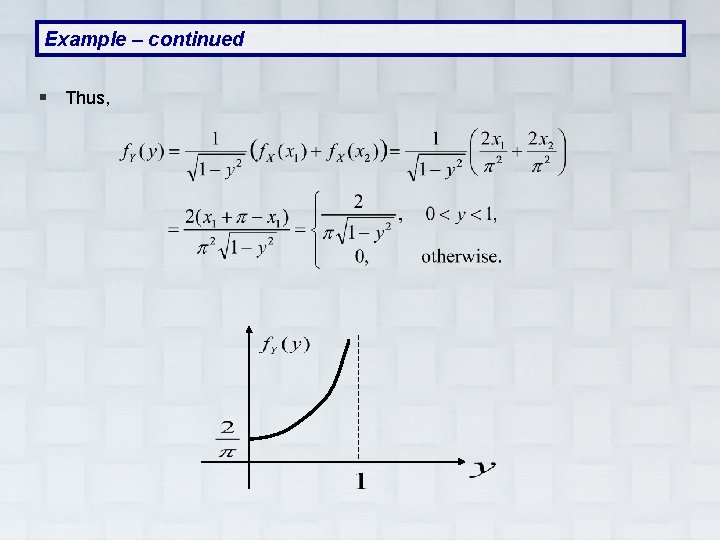
Example – continued § Thus,

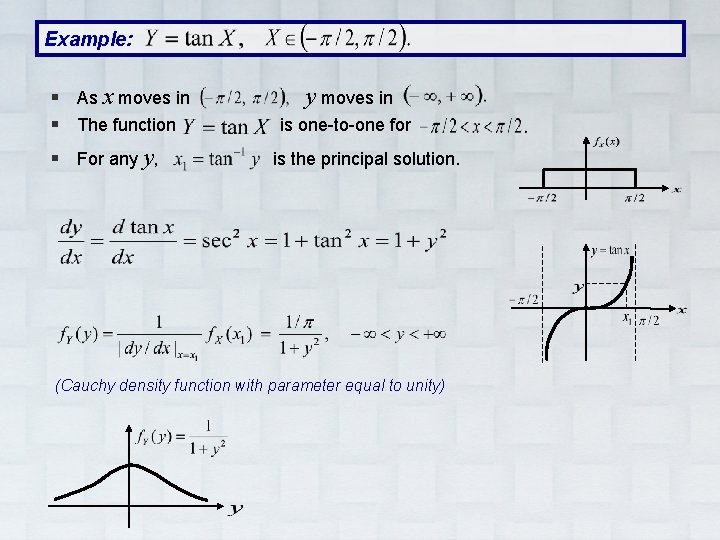
Example: § As x moves in § The function § For any y, y moves in is one-to-one for is the principal solution. (Cauchy density function with parameter equal to unity)

Functions of a Discrete-type R. V § Suppose X is a discrete-type r. v with § and § Clearly Y is also of discrete-type, and when and for those s,

Example § Suppose so that § Define Find the p. m. f of Y. § Solution: X takes the values § Y only takes the values § so that for