Functions Functions have EXACTLY ONE output for each











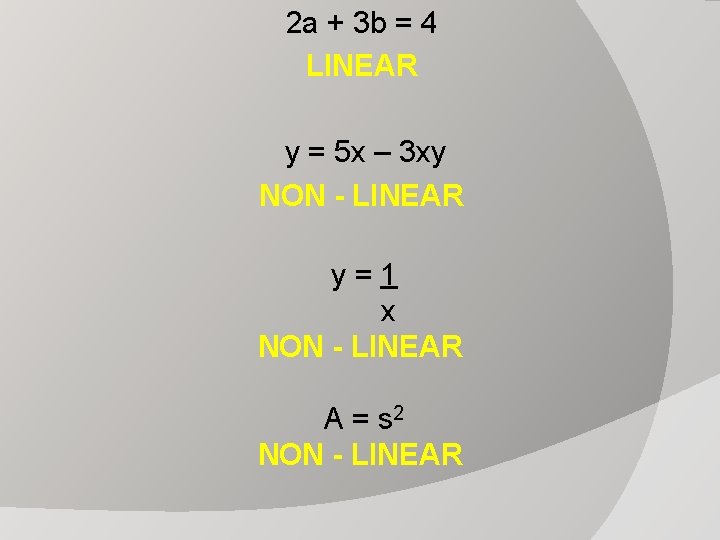
- Slides: 23

Functions: Functions have EXACTLY ONE output for each input – **Each input can match up to only one output Examples: ATM Vending Machine Gas Station Calculator Pencil Sharpener Phone CD Player Oven Key – Lock Remote Control Keyboard

INPUT / OUTPUT INPUT: The value substituted into an expression or function OUTPUT: The value that results from the substitution of a given input into an expression or function.

*MAPPING* Function: Non-Function:

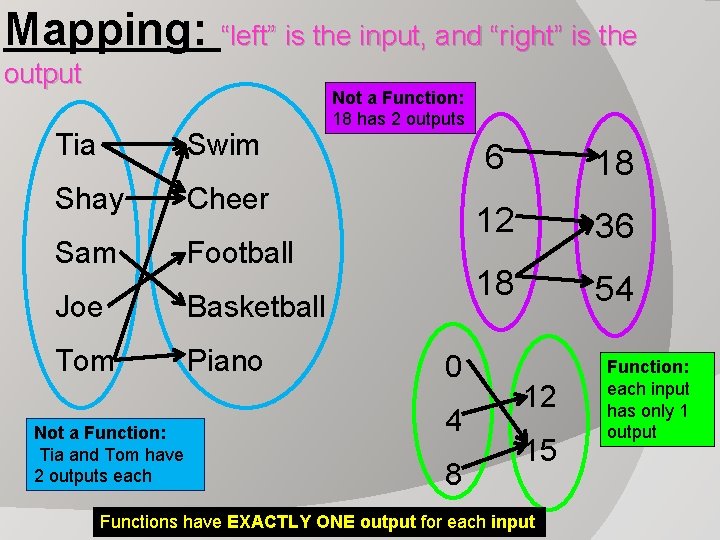
Mapping: “left” is the input, and “right” is the output Tia Swim Shay Cheer Sam Football Joe Basketball Tom Piano 0 4 8 6 18 12 36 18 54 12 15 Functions have EXACTLY ONE output for each input

Mapping: “left” is the input, and “right” is the output Tia Swim Shay Cheer Sam Football Joe Basketball Tom Piano Not a Function: Tia and Tom have 2 outputs each Not a Function: 18 has 2 outputs 0 4 8 6 18 12 36 18 54 12 15 Functions have EXACTLY ONE output for each input Function: each input has only 1 output

Function: *TABLES* Non-Function:

Tables: “x” is the input, and “y” is the output. For a table to represent a function, a number can show up in the x column only one time (input), but in the y column many times (output). x 2 3 5 4 y 8 9 10 11 x 1 2 2 3 y 3 2 10 4 Functions have EXACTLY ONE output for each input

*ORDERED PAIRS* Don’t forget that a relation has brackets { } on the outsides and parenthesis ( ) around each set. Function: Non-Function:

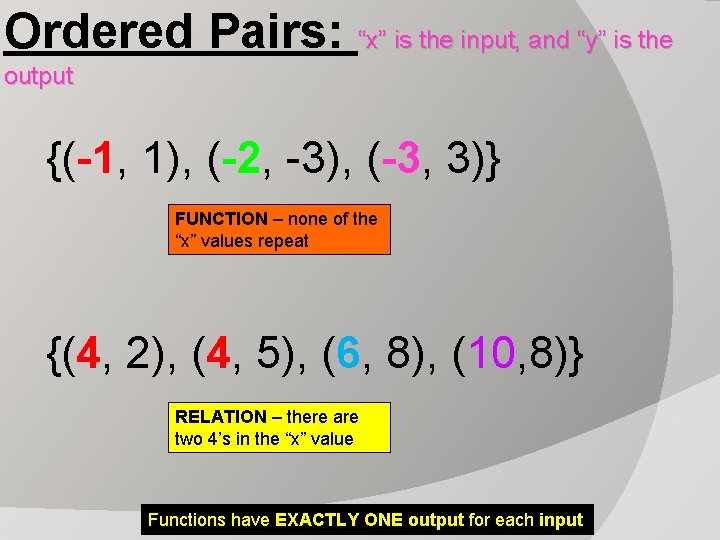
Ordered Pairs: “x” is the input, and “y” is the output {(-1, 1), (-2, -3), (-3, 3)} {(4, 2), (4, 5), (6, 8), (10, 8)} Functions have EXACTLY ONE output for each input

Ordered Pairs: “x” is the input, and “y” is the output {(-1, 1), (-2, -3), (-3, 3)} FUNCTION – none of the “x” values repeat {(4, 2), (4, 5), (6, 8), (10, 8)} RELATION – there are two 4’s in the “x” value Functions have EXACTLY ONE output for each input

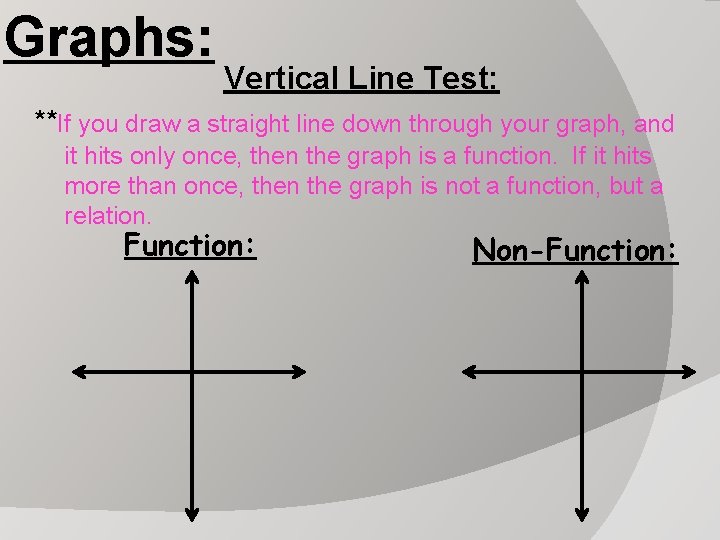
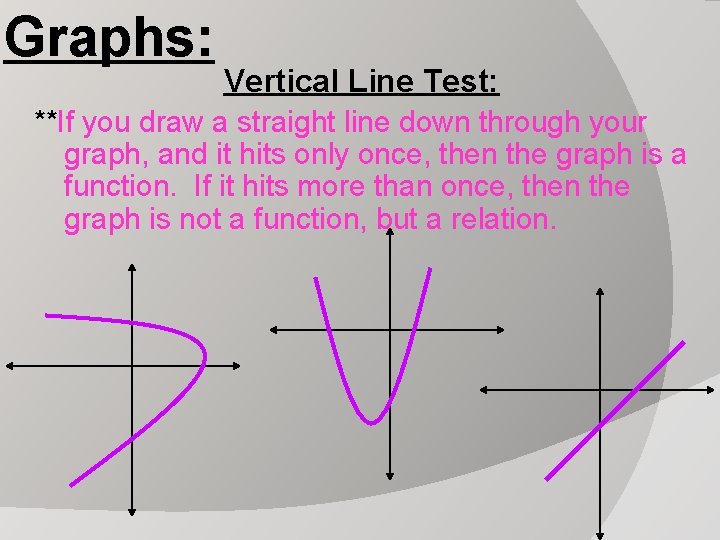
Graphs: Vertical Line Test: **If you draw a straight line down through your graph, and it hits only once, then the graph is a function. If it hits more than once, then the graph is not a function, but a relation. Function: Non-Function:

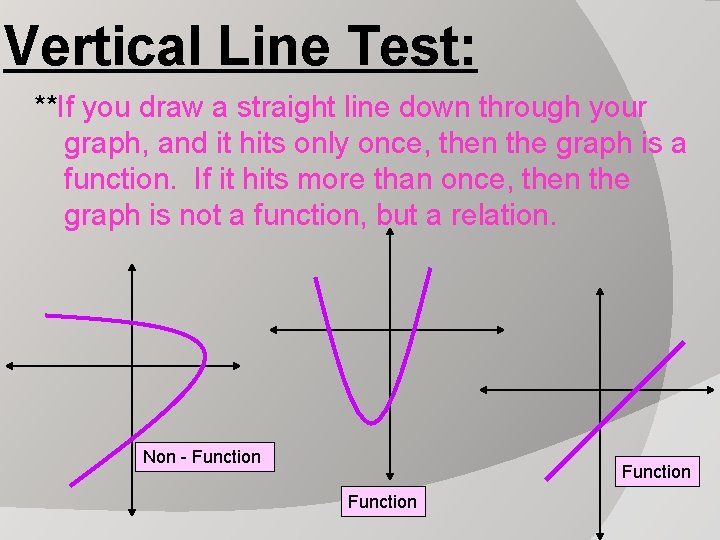
Graphs: Vertical Line Test: **If you draw a straight line down through your graph, and it hits only once, then the graph is a function. If it hits more than once, then the graph is not a function, but a relation.

Vertical Line Test: **If you draw a straight line down through your graph, and it hits only once, then the graph is a function. If it hits more than once, then the graph is not a function, but a relation. Non - Function

Linear vs. Non Linear:

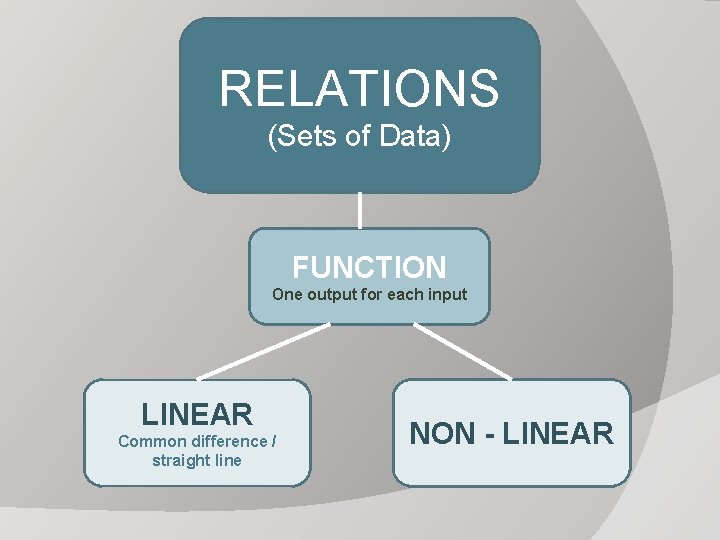
RELATIONS (Sets of Data) FUNCTION One output for each input LINEAR Common difference / straight line NON - LINEAR

Linear or Non-Linear Only functions are linear. For a function to be linear, there has to be a common difference – this means to look at the outputs, and if you get the same solution when you subtract, you have a common difference. Linear functions, when graphed, form a straight line.

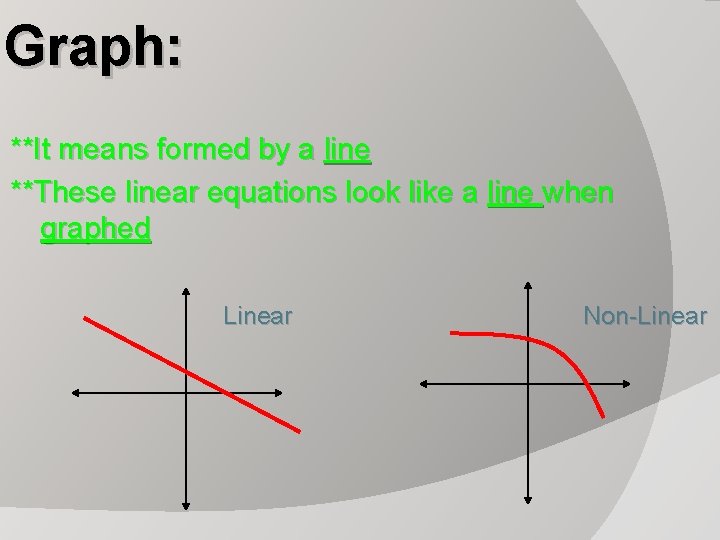
Graph: **It means formed by a line **These linear equations look like a line when graphed Linear Non-Linear

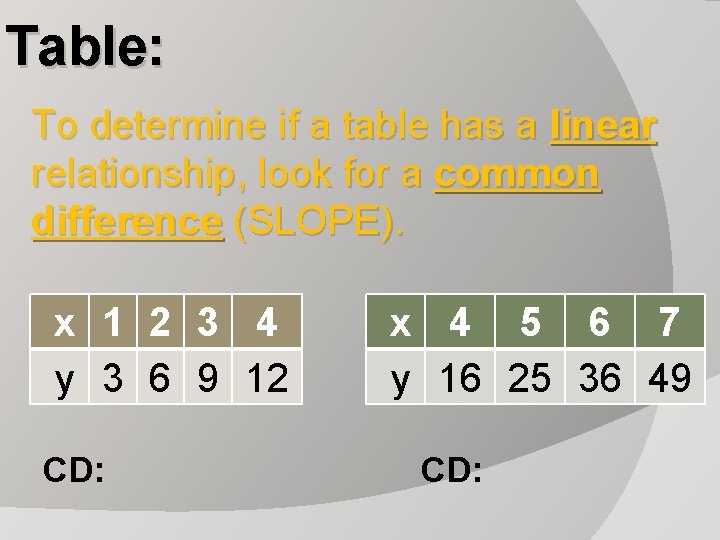
Table: To determine if a table has a linear relationship, look for a common difference (SLOPE). x 1 2 3 4 y 3 6 9 12 CD: x 4 5 6 7 y 16 25 36 49 CD:

Equation: � 3 checks = LINEAR

Is it Linear? ? *When looking at a graph, graph if it makes a straight line, IT’S LINEAR. *When looking at a table, table if there is a common difference, IT’S LINEAR. *When looking at an equation, equation if there are no exponents, no variables multiplied together, and no variables in the denominator, IT’S LINEAR.

Ticket Out The Door… On your sticky note, write down if you think the following functions are LINEAR or NON - LINEAR

*No Exponents *No variables being multiplied together *No variable in denominator 2 a + 3 b = 4 y = 5 x – 3 xy y=1 x A = s 2
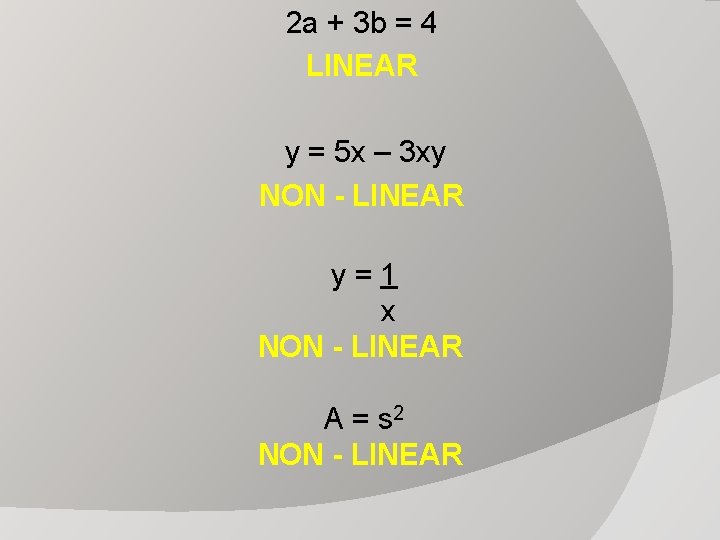
2 a + 3 b = 4 LINEAR y = 5 x – 3 xy NON - LINEAR y=1 x NON - LINEAR A = s 2 NON - LINEAR