Functions and Their Representation Lesson 1 3 What

Functions and Their Representation Lesson 1. 3

What is a Function l l A relationship between two quantities Reperesented by: l l A table x 7 2 9 3 y 8 4 0 5 A formula A = r 2 A description A graph

Definition of a Function l Mathematical definition: A set of ordered pairs where no two ordered pairs have the same first element

Evaluating Possible Functions l Which is a function? l {(2, 3), (4, 7), (9, 3)} {(2, 3), (4, 7), (2, 9)} {(2, 3), (4, 7), (9, 2)}

Function Notation l If we say “R is a function of t” the notation is … R = f(t) l Note: f(t) does not mean f * t

Using Function Notation l l Suppose we say h(t) = -16 t 2 +64 t The height of a ball thrown into the air is a function of t, time We evaluate functions by substituting a value for time into the formula That is l l h(3) = -16*32 + 64*3 Which evaluates to ? ? ?

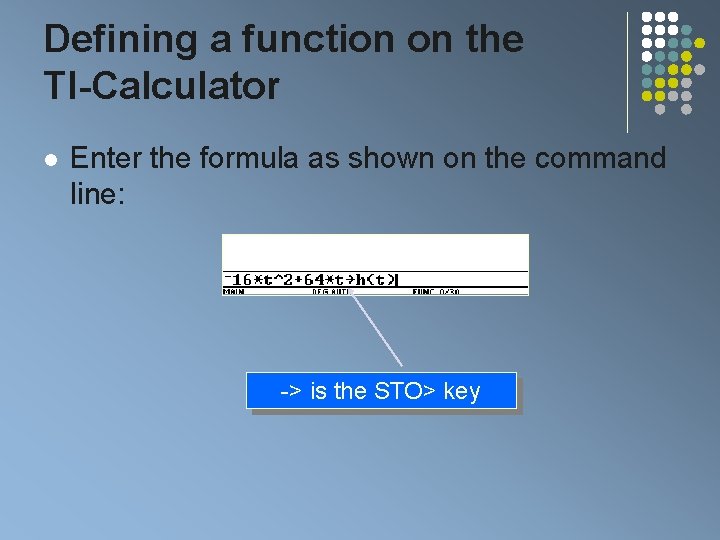
Defining a function on the TI-Calculator l Enter the formula as shown on the command line: -> is the STO> key

Using TI-Calculator Functions l On the entry line enter h(3) l l Press <enter> Try evaluating the function h(t) for different values of t l l l h(7) h(-4) h(x+2)

Using TI-Calculator Functions l Graphing the funciton l l l Go to the Y= screen (♦W) Enter in the function – you must use x's as the independent variable Options l l Enter function entirely Reference a previously defined function

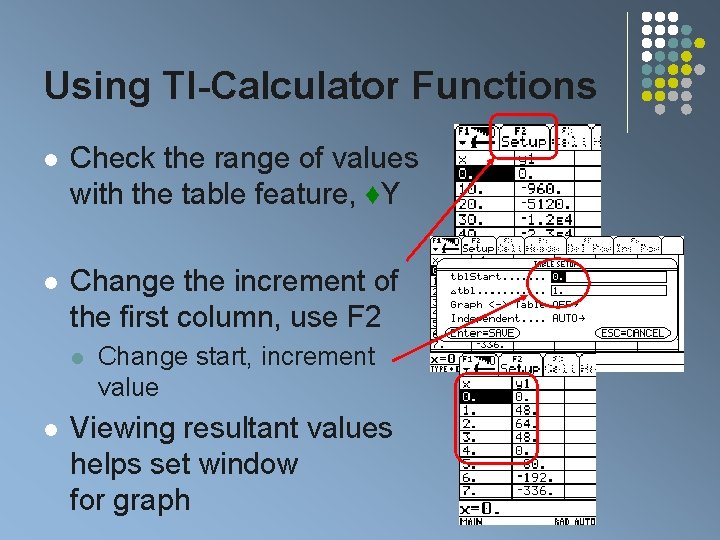
Using TI-Calculator Functions l Check the range of values with the table feature, ♦Y l Change the increment of the first column, use F 2 l l Change start, increment value Viewing resultant values helps set window for graph

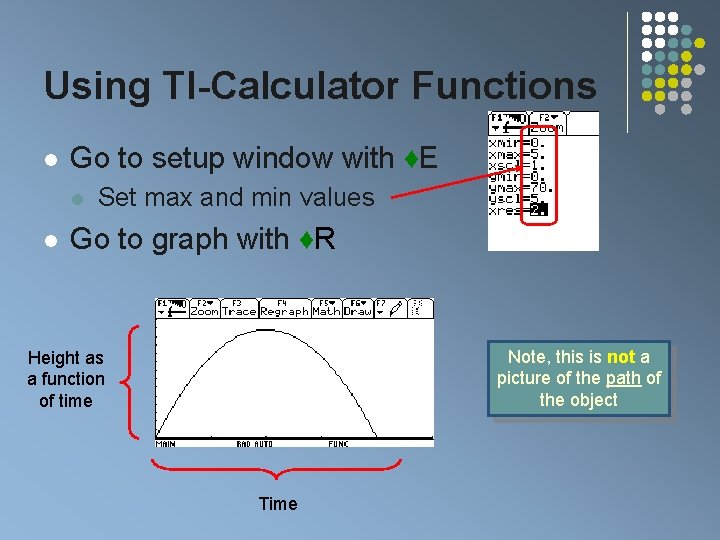
Using TI-Calculator Functions l Go to setup window with ♦E l l Set max and min values Go to graph with ♦R Note, this is not a picture of the path of the object Height as a function of time Time

Assignment l l l Lesson 1. 3 Page 38 Exercises l 1 – 77 EOO