Functions and Graphs CHAPTER 1 SECTION 2 Increasing

Functions and Graphs CHAPTER 1, SECTION 2

Increasing and Decreasing Functions increasing functions rise from left to right any two points within this interval must have a positive slope decreasing functions fall from left to right any two points within this interval must have a negative slope constant functions follow a horizontal path from left to right any two points within this interval must have a zero slope one function can follow increasing, decreasing, and constant patterns

Identify intervals on which the following functions are increasing, decreasing, and constant.

Boundedness bounded below a function is bounded below if there is some number b that is less than or equal to every number in the range of the function this number is called a lower bound same idea as a minimum bounded above a function is bounded above if there is some number b that is greater than or equal to every number in the range of the function this number is called an upper bound same idea as a maximum bounded – a function is bounded if it is bounded above and below

Determine whether the function is bounded above, bounded below, or bounded.

Local and Absolute Extrema local/relative maxima – a function has a local/relative maxima if there is some value f(x) that is greater than or equal to all range values in some interval of the function if the point is greater than or equal to all range values, it is called the absolute maxima local/relative minima – a function has a local/relative minima if there is some value f(x) that is less than or equal to all range values in some interval of the function if the point is less than or equal to all range values, it is called the absolute minima these points are also a part of what is called critical points of functions

Symmetry basic definition: the graph looks the same when folded according to the line of symmetry Symmetric with respect to the y-axis Graphs that are symmetric with the y-axis are considered even functions, f(-x)=f(x) Symmetric with respect to the x-axis Graphs that are symmetric with the x-axis are not functions, f(x)=-f(x) Symmetric with respect to the origin Graphs that are symmetric with the origin are considered odd functions, f(-x)=-f(x)

Determine whether the functions are even, odd, or neither and describe their symmetry.

Horizontal Asymptotes Horizontal asymptotes A line y=b that the graph approaches but never crosses For rational functions: If degree of num. >degree of den. , then there is NO horizontal asymptote. If degree of num. <degree of den. , then y=0 is the horizontal asymptote If degrees are equal, then the ratio of leading coefficients is the horizontal asymptote Can be found by examining the graph and looking for the yvalue the graph is approaching from both directions, but isn’t crossing.

Vertical Asymptotes Vertical asymptotes A line x=a that the graph approaches but never crosses Recall to find: find the value that makes the denominator=0, look for error on the table, look for an infinite discontinuity on the graph. *Functions can have both vertical and horizontal asymptotes *Some functions DO cross their asymptotes *Some functions have more than one horizontal asymptote – they cannot have more than 2 WHY? – extra credit

Find all horizontal and vertical asymptotes of the functions below.

What can we determine from a graph? Domain Range X-intercepts Y-intercepts Increasing, decreasing, constant intervals Values for x Values for y or f(x) Max/min Symmetry Discontinuities, asymptotes boundedness

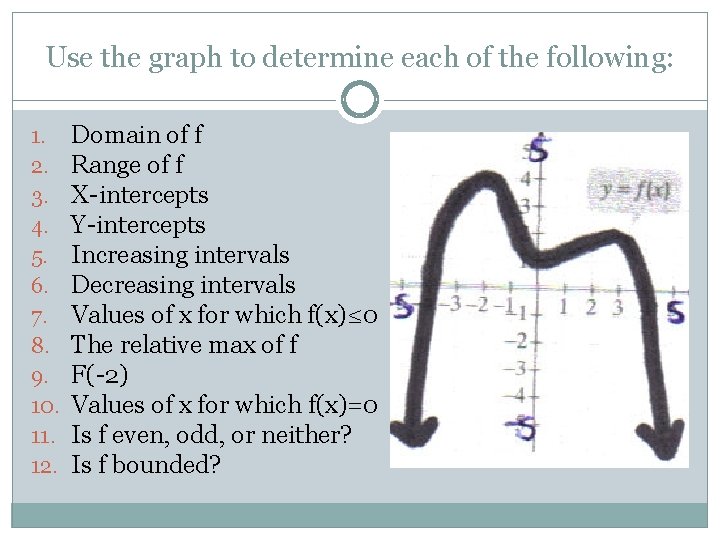
Use the graph to determine each of the following: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Domain of f Range of f X-intercepts Y-intercepts Increasing intervals Decreasing intervals Values of x for which f(x)≤ 0 The relative max of f F(-2) Values of x for which f(x)=0 Is f even, odd, or neither? Is f bounded?

In conclusion Exit Slip: With a partner, complete problem 80 on page 100 of your textbook Homework: