Functional Verification III Software Testing and Verification Lecture

Functional Verification III Software Testing and Verification Lecture Notes 23 Prepared by Stephen M. Thebaut, Ph. D. University of Florida

Previously… • Correctness conditions and working correctness questions: – sequencing – decision statements

Today’s Topics • Iteration Recursion Lemma (IRL) • Termination predicate: term(f, P) • Correctness conditions for while_do statement • Sufficient correctness conditions • Correctness conditions for repeat_until statement • Subgoal Induction

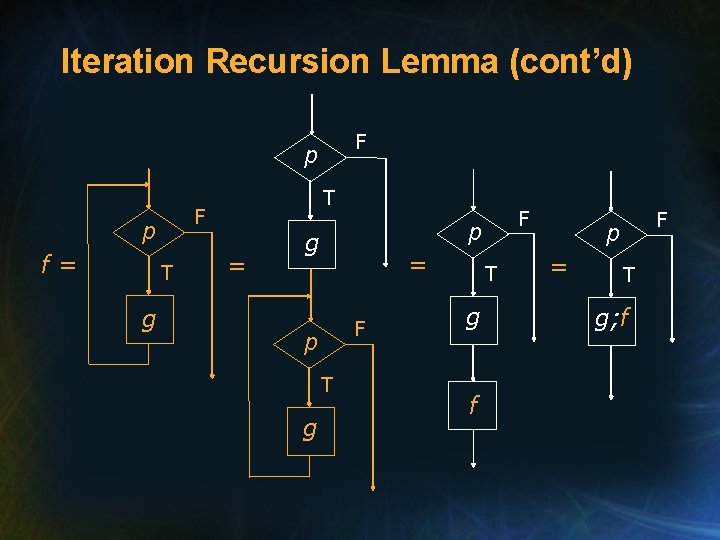
Iteration Recursion Lemma (IRL) • The IRL reduces the verification of programs with loops to a question of termination and the verification of loopfree programs by converting iteration to recursion. • For while loops, the Lemma states: f = [while p do g] = [if p then g; f end_if] (note recursion)

Iteration Recursion Lemma (cont’d) F p f= T g T = p g = F p T g F T g f F p = T g; f

Iteration Recursion Lemma (cont’d) • Rather than verify directly that f is the program function of K = while p do g which can be very difficult, it is sufficient to prove that 1. K terminates for all X D(f), and that 2. f is the program function of Q = if p then g; f end_if because [K] = [Q].

An important implication of the IRL • Suppose for “input” X 0 the while loop terminates after n iterations with “output” Xn. • Furthermore, let X 1, X 2, . . . , Xn-1 be the intermediate states generated by the loop. • Then 0≤i<n, we know: – p(Xi), – Xi+1=g(Xi), and – ¬p(Xn).

An important implication of the IRL (cont’d) • As f = [while p do g] = [if p then g; f end_if], it follows that f(X 0) = f(X 1) =. . . = f(Xn) = Xn • More generally, after each iteration of the loop, the function value of the current state, X, must be the same as the function value of the initial state, X 0. That is: f(X) = f(X 0) • We will revisit this observation in connection with Mill’s Invariant Status Theorem later.

Illustrative Example of IRL • To further illustrate the fact that [while p do g] = [if p then g; f end_if] consider a concrete example. . . • Let K = while y>0 do x, y : = x+1, y− 1 p g • Claim: K is function equivalent to Q = if y>0 then x, y : = x+1, y− 1; k end_if p kog where, by definition, k = [K].

Illustrative Example of IRL (cont’d) Case (y>0): For K = while y>0 do x, y : = x+1, y− 1, the loop body executes y times before the predicate y>0 becomes false. By observation, the final value of x is x 0+(1)y 0 = x 0+y 0 and the final value of y is 0. Thus, (y>0) => k = (x, y : = x+y, 0) Also, note that when y=0 initially, k = I = (x, y : = x, y) = (x, y : = x+0, y) = (x, y : = x+y, 0) Therefore, (y≥ 0) => k = (x, y : = x+y, 0)

Illustrative Example of IRL (cont’d) Case (y>0): (cont’d) [Q] is a composition of two functions, i. e. , k o g, and may be determined by direct substitution. For y>0 initially, y will be greater than OR EQUAL to 0 after executing the loop body, but since we know (y≥ 0) => k = (x, y : = x+y, 0), we have [Q] = (x, y : = x+y, 0) o (x, y : = x+1, y− 1) = (x, y : = (x+1)+(y− 1), 0) = (x, y : = x+y, 0) = k (the function computed by K) Thus, [Q] = [K] when y>0.

Illustrative Example of IRL (cont’d) Case (y≤ 0): Since the predicate (y>0) fails, both K and Q do nothing, and are therefore equivalent. Thus, [Q] = I = [K] when y≤ 0. Therefore, K is function equivalent to Q.

Termination Predicate • The correctness of a looping program P depends, in part, on termination. • Consideration is limited to programs whose termination can be established and the following predicate is defined: term(f, P) ‘‘P terminates for every initial state X D(f)’’

Before we continue… • Take out a piece of paper and a pen/pencil. • Without looking back in the lecture notes, write down the complete correctness conditions for: f = [if p then g]

if_then Correctness Conditions • Complete correctness conditions for f = [if p then g]: Prove: p (f = g) Л ¬p (f = I) • So, aside from proving termination over the domain of f, what are the two corresponding conditions for: f = [while p do g] = [if p then fog] ?

while_do Correctness Conditions • Complete correctness conditions for f = [K] = [while p do G] (where g = [G] has already been shown): Prove: term(f, K) Л p (f = f o g) Л ¬p (f = I)

while_do Correctness Conditions (cont’d) • Working correctness questions: – Is loop termination guaranteed for any argument of f ? – When p is true does f equal f composed with g? – When p is false does f equal Identity?

while_do Example • Prove f = [T] where, for integers x, y, and z: f = (y≥ 0 z, y : = z+xy, 0) and T is: p while y<>0 do z : = z+x y : = y− 1 G end_while

while_do Example (cont’d) • Proof: g = [G] = (z, y : = z+x, y− 1) by observation – term(f, T)? f = (y≥ 0 z, y : = z+xy, 0) and T is: while y<>0 do z : = z+x y : = y− 1 end_while So, does y≥ 0 initially T will terminate?

while_do Example (cont’d) • Proof: g = [G] = (z, y : = z+x, y− 1) by observation – term(f, T)? √ (Prove this…)

while_do Example (cont’d) • Proof: g = [G] = (z, y : = z+x, y− 1) by observation – term(f, T)? √ (Prove this…) – Does (y=0) ( f = I )? ¬p ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) • Proof: g = [G] = (z, y : = z+x, y− 1) by observation – term(f, T)? √ (Prove this…) – Does (y=0) ( f = I )? √ (y=0) ( f = (z, y : = z+x(0), 0) = (z, y : = z, 0) ) (y=0) ( I = (z, y : = z, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? p

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case a: Does (y<0) ( f = f o g )? (y<0) ( f = undefined ) (y<0) ( f o g = f o (z, y : = z+x, y− 1) What is f when applied after g decrements the initially negative value of y? ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case a: Does (y<0) ( f = f o g )? (y<0) ( f = undefined ) (y<0) ( f o g = undefined o (z, y : = z+x, y− 1) since y<0 gy(y<0)<0 ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case a: Does (y<0) ( f = f o g )? (y<0) ( f = undefined ) (y<0) ( f o g = undefined o (z, y : = z+x, y− 1) = undefined )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case a: Does (y<0) ( f = f o g )? √ (y<0) ( f = undefined ) (y<0) ( f o g = undefined o (z, y : = z+x, y− 1) = undefined )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case b: Does (y>0) ( f = f o g )? ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case b: Does (y>0) ( f = f o g )? (y>0) ( f = (z, y : = z+xy, 0) ) (y>0) ( f o g = f o (z, y : = z+x, y− 1) Again, what is f when applied after g decrements the initially positive value of y? ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case b: Does (y>0) ( f = f o g )? (y>0) ( f = (z, y : = z+xy, 0) ) (y>0) ( f o g = (z, y : = z+xy, 0) o (z, y : = z+x, y− 1) since y>0 gy(y>0)≥ 0 ( Recall: f = (y≥ 0 z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case b: Does (y>0) ( f = f o g )? (y>0) ( f = (z, y : = z+xy, 0) ) (y>0) ( f o g = (z, y : = z+xy, 0) o (z, y : = z+x, y− 1) = (z, y : = (z+x)+x(y− 1), 0) = (z, y : = z+xy, 0) )

while_do Example (cont’d) – Does (y 0) ( f = f o g )? case b: Does (y>0) ( f = f o g )? (y>0) ( f = (z, y : = z+xy, 0) ) (y>0) ( f o g = (z, y : = z+xy, 0) o (z, y : = z+x, y− 1) = (z, y : = (z+x)+x(y− 1), 0) = (z, y : = z+xy, 0) ) We could have also composed the full, conditional definition of f with g, i. e. (y≥ 0 z, y : = z+xy, 0) o (z, y : = z+x, y− 1) to yield (y≥ 1 z, y : = z+xy, 0) which is just (z, y : = z+xy, 0) when y>0.

while_do Example (cont’d) – Does (y 0) ( f = f o g )? √ case b: Does (y>0) ( f = f o g )? √ (y>0) ( f = (z, y : = z+xy, 0) ) (y>0) ( f o g = (z, y : = z+xy, 0) o (z, y : = z+x, y− 1) = (z, y : = (z+x)+x(y− 1), 0) = (z, y : = z+xy, 0) ) Therefore, f = [T].

Exercise 1 • For program M below, where all variables are integers, hypothesize a function f for [M] and prove f = [M]. while i<n do t : = t*x i : = i+1 end_while

Sufficient Correctness Conditions • Given the complete correctness conditions for f = [H] = [while p do g]: Prove: term(f, H) Л p (f = f o g) Л ¬p (f = I)

Sufficient Correctness Conditions (cont’d) What are the sufficient correctness conditions for f [H] = [while p do g]? Prove: f’ = [H] for some f’ Л f f’

Sufficient Correctness Conditions (cont’d) What are the sufficient correctness conditions for f [H] (for ANY program, H)? Prove: f’ = [H] for some f’ Л f f’

repeat_until Statement • What are the complete correctness conditions for f = [R] = [repeat g until p]? g f= p F T

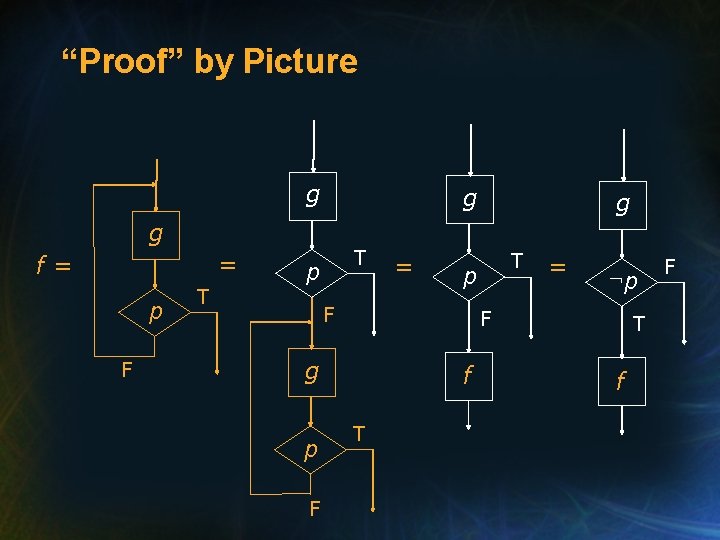
repeat_until Statement (cont’d) • An IRL for repeat_until statements: f = [repeat g until p] = [g; if ¬p then f]

“Proof” by Picture g g = f= p F T p T = F F = ¬p F g p T p f T T f F

repeat_until Statement (cont’d) • Therefore, it is sufficient to verify that 1. R terminates for all X D(f), and that 2. f is the program function of Q = g; if ¬p then f end_if because [R] = [Q].

repeat_until Correctness Conditions • Complete correctness conditions for f = [R] = [repeat G until p] (where g = [G] has already been shown): Prove: term(f, R) Л (p o g) (f = g) Л ¬(p o g) (f = f o g)

repeat_until Correctness Conditions (cont’d) • Working correctness questions: – Is loop termination guaranteed for any argument of f ? – When p o g is true does f equal g? – When p o g is false does f equal f o g?

Exercise 2 • For program R below, where all variables are integers, hypothesize a function r for [R] and prove r = [R]. repeat: x : = x− 1 y : = y+2 until x=0

Summary • Iteration Recursion Lemma (IRL) • Termination predicate: term(f, P) • Correctness conditions for while_do statement • Sufficient correctness conditions • Correctness conditions for repeat_until statement • Subgoal Induction

Coming up next… • Thinking about invariants again • Invariant Status Theorem (IST) • While Loop Initialization • Utility of IST

Functional Verification III Software Testing and Verification Lecture Notes 23 Prepared by Stephen M. Thebaut, Ph. D. University of Florida