Functional Skills Maths An introduction to Pythagoras theorem

Functional Skills Maths An introduction to Pythagoras’ theorem for building (roofing) students February 2013. Kindly contributed by Louise Dumbell. Search for Louise on www. skillsworkshop. org Please refer to the download page for this resource on skillsworkshop. org for detailed curriculum links and related resources. Curriculum links Adult Numeracy N 1/L 2. 4: Evaluate expressions and make substitutions in given formulae in words and symbols to produce results Underpins the following L 2 Functional Maths coverage & range statements Understand use simple formulae and equations involving one- or two-step operations. Carry out calculations with numbers of any size in practical contexts, to a given number of decimal places References: Excellence Gateway (2009), Skills for Life, Core Curriculum http: //www. excellencegateway. org. uk/sflcurriculum Ofqual (2009), Functional Skills criteria for English, Mathematics and ICT http: //www 2. ofqual. gov. uk/qualifications-assessments/89 -articles/238 -functional-skills-criteria

Pythagoras’ Theorem Please note this is an animated PPT and should be run full screen

Square and square root of numbers • • • What does 32 mean? 3 x 3=9 What does 42 mean? 4 x 4 = 16 What does 102 mean? 10 x 10 = 100

Square and square root of numbers • What does the symbol mean? • Square root – i. e. What number do you multiple by itself to get the original number? • What is √ 4 ? • 2 x 2=4 so the √ 4 is 2 • What is √ 9 ? • 3 x 3=9 so the √ 9 is 3

Pythagoras’ Theorem • What is Pythagoras’ Theorem used for? • Given 2 sides of a right angled triangle to calculate the 3 rd. • What is a right angled triangle? • What is the side opposite the right angle called? • Hypotenuse

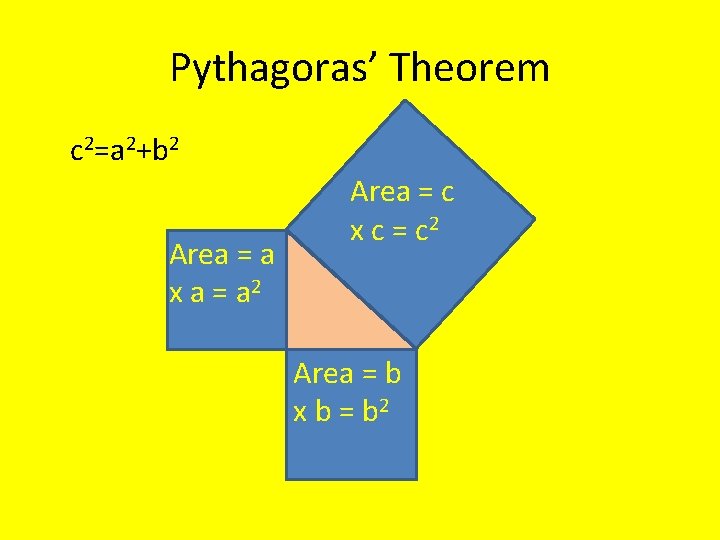
Pythagoras’ Theorem c 2=a 2+b 2 Area = a x a = a 2 Area = c x c = c 2 Area = b x b = b 2

Pythagoras’ Theorem • If “c” is the hypotenuse and “a” and “b” are the other 2 sides then: • c 2=a 2+b 2

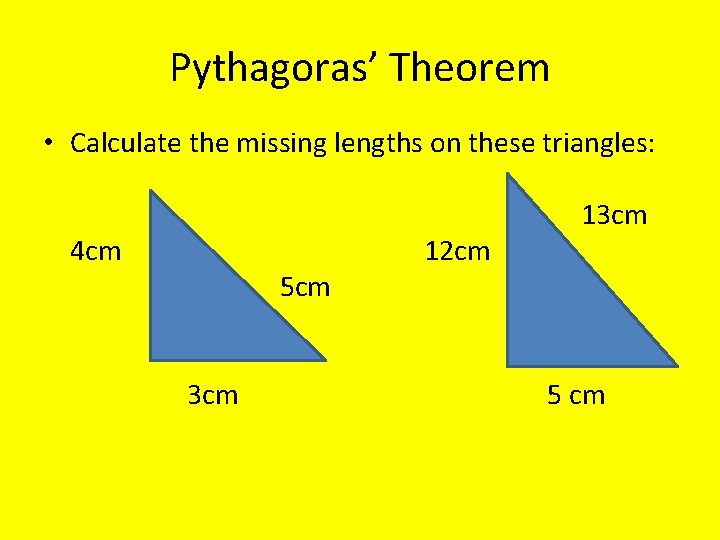
Pythagoras’ Theorem • Calculate the missing lengths on these triangles: 4 cm 5 cm 3 cm 12 cm 13 cm 5 cm

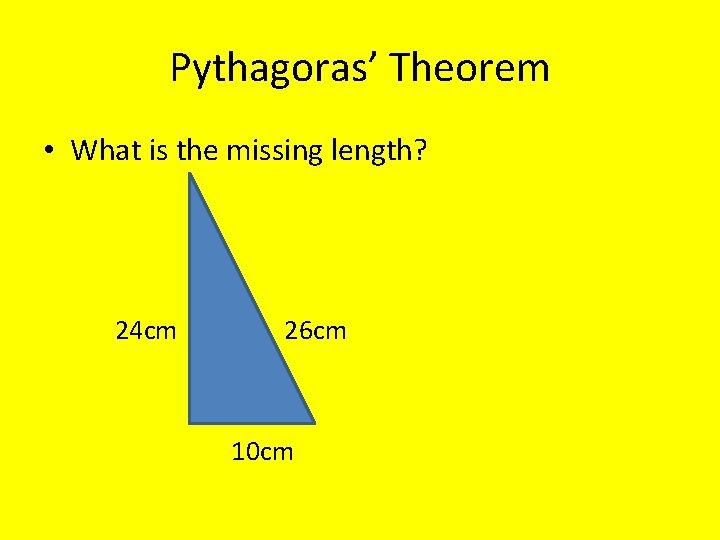
Pythagoras’ Theorem • What is the missing length? 24 cm 26 cm 10 cm

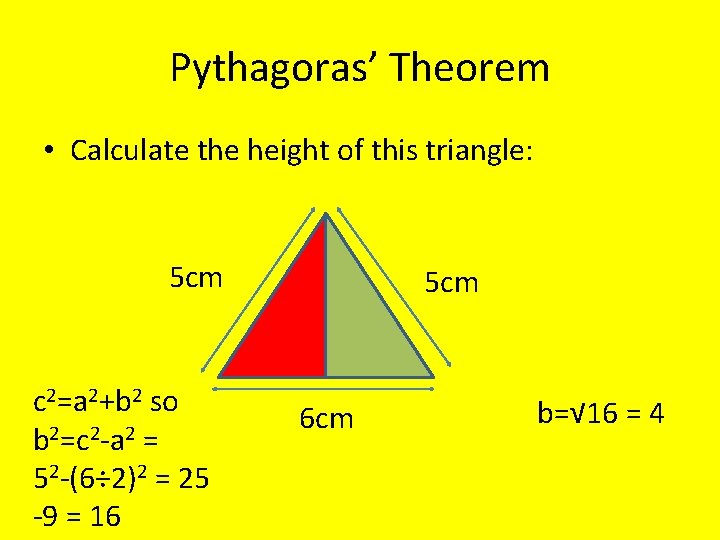
Pythagoras’ Theorem • Calculate the height of this triangle: 5 cm c 2=a 2+b 2 so b 2=c 2 -a 2 = 52 -(6÷ 2)2 = 25 -9 = 16 5 cm 6 cm b=√ 16 = 4

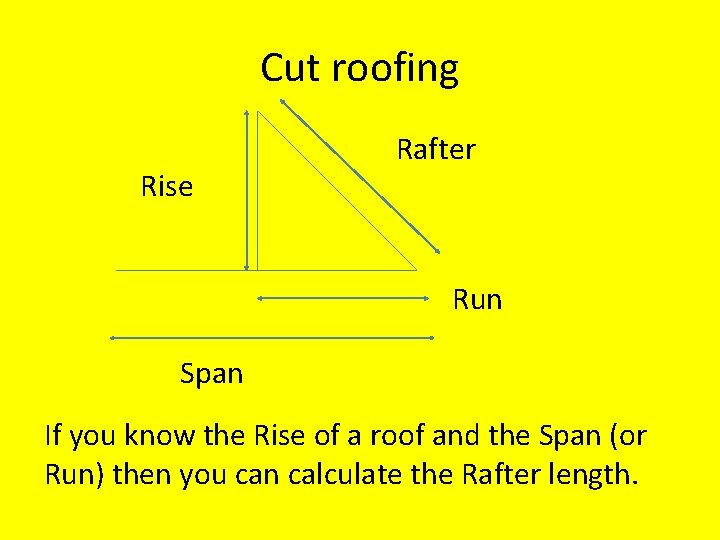
Cut roofing Rise Rafter Run Span If you know the Rise of a roof and the Span (or Run) then you can calculate the Rafter length.

Rafter Lengths • If a roof has a rise of 4 m and a run of 3 m, what length rafters do you need? • Answer: 5 m

Rafter Lengths • If a roof has a rise of 6 m and a run of 8 m, what length rafters do you need? • Answer: 10 m

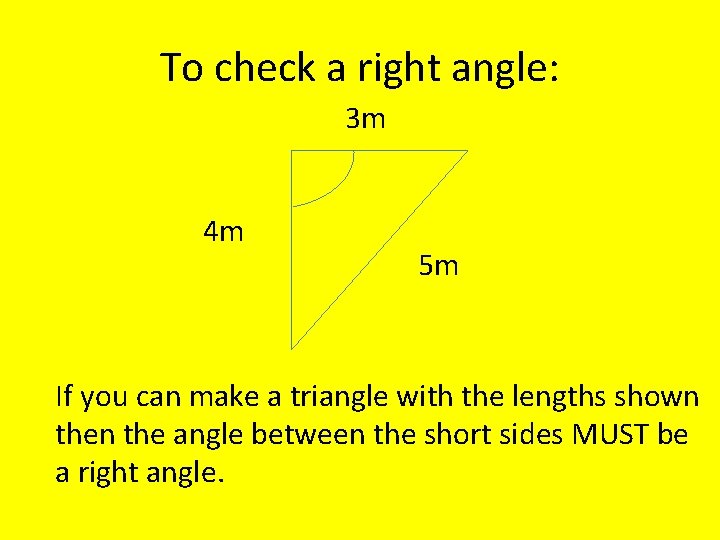
To check a right angle: 3 m 4 m 5 m If you can make a triangle with the lengths shown the angle between the short sides MUST be a right angle.