Functional Programming in Haskell Motivation through Concrete Examples

Functional Programming in Haskell Motivation through Concrete Examples Adapted from Lectures by Simon Thompson Prasad CS 776

Functional Programming Given the functions above invert. Colour flip. H side. By. Side superimpose flip. V and the horse picture, how do you get … (expression and evaluation) Prasad CS 776 2

Definitions in Haskell name : : Type name = expression black. Horse : : Picture black. Horse = invert. Colour horse rotate : : Picture -> Picture rotate pic = flip. H (flip. V pic) Prasad CS 776 3

Higher-level Evaluation is about expressions and values, not storage locations. • No need to allocate/deallocate storage: garbage collection. • Values don't change over program execution: contrast x=x+1 etc. of Java, C, … • … instead we describe relations between values by means of (fixed) functions. Prasad CS 776 4

Declarative … proofs possible Programs describe themselves: square n = n*n double n = 2*n 'The square of n is n*n, for every integer n. ' Programs are equations. So we can write proofs using the definitions. square (double n) = square (2*n) = (2*n)*(2*n) = 2*2*n*n = double (square n)) Prasad CS 776 5

Evaluation freedom Evaluation can occur in any order. . . (4 -3)+(2 -1) (4 -3)+1 (4 -3)+(2 -1) 1+1 1+1 2 2 (4 -3)+(2 -1) 1+1 2 … and can choose to evaluate only what is needed, when it is needed: lazy evaluation (more later). Can also evaluate in parallel … efficiently? Prasad CS 776 6

History First 'functional' language, LISP, defined c. 1960 … popular in AI in 70 s/80 s. • Now represented best by Scheme. • Weakly typed; allows side-effects and eval. Next generation: ML (1980…), Miranda (1985…) and Haskell (1990…). • Strongly-typed; ML allows references and thus side-effects. • Miranda and Haskell: pure and lazy. • FP (1982): heroic experiment by Backus (FORTRAN, ALGOL). Prasad CS 776 7

Haskell and Hugs Named after Haskell Brooks Curry: mathematician and logician; inventor of the -calculus. Haskell 98 is the recent 'standard' version of Haskell. Various implementations: Hugs (interpreter for Windows, Mac, Unix) and GHC, NHC, HBC (compilers). http: //www. haskell. org/ Prasad CS 776 8

Basics: guards and base types How many of three integers are equal … ? how. Many. Equal : : Int -> Int how. Many. Equal n m k | n==m && m==k = 3 | n==m || m==k || k==n = 2 | otherwise = 1 … and if we reach here they're all different. If we reach here they're not all equal …

Regular and literate scripts In a regular script there are definitions and comments: In a literate script there are comments and definitions: -- First. Script. hs First. Lit. lhs -- 5 October 2000 -- Double an integer. double : : Int -> Int > double : : Int -> Int double n = 2*n > double n = 2*n Everything is program, except comments beginning --. Prasad Everything is comment, except program beginning >. CS 776 10

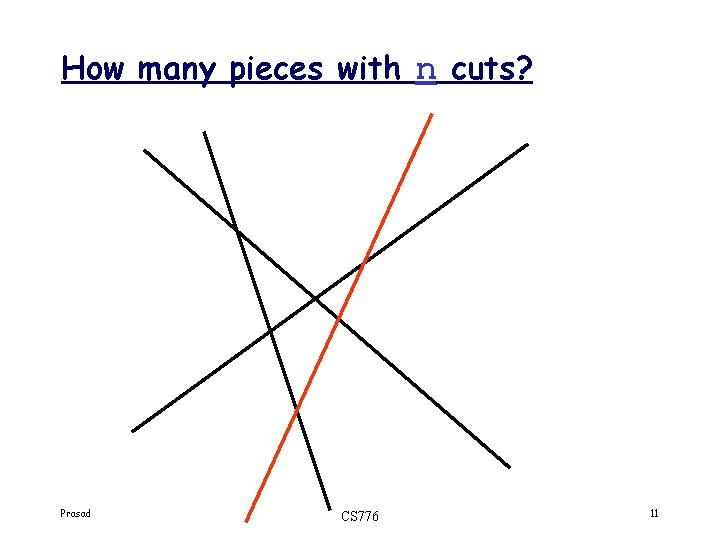
How many pieces with n cuts? Prasad CS 776 11

How many pieces with n cuts? No cuts: 1 piece. With the nth cut, you get n more pieces: cuts : : Int -> Int cuts n Prasad | n==0 = 1 | n>0 = cuts (n-1) + n | otherwise = 0 CS 776 12

The Pictures case study. Using a powerful library of functions over lists. • Pattern matching • Recursion • Generic functions • Higher-order functions • … Prasad CS 776 13

Using Hugs expr Evaluate expr : type expr Give the type of expr : l Blah Load the file Blah. hs : r Reload the last file : ? Help: list commands : e Edit the current file : q Quit Prasad CS 776 14

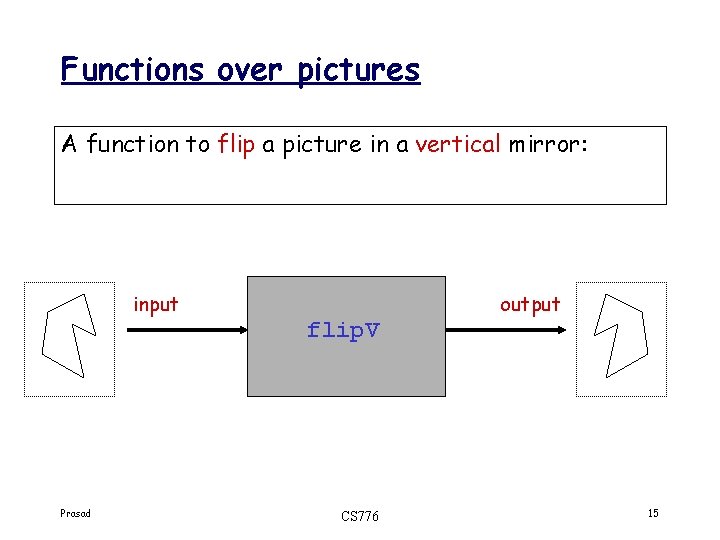
Functions over pictures A function to flip a picture in a vertical mirror: input output flip. V Prasad CS 776 15

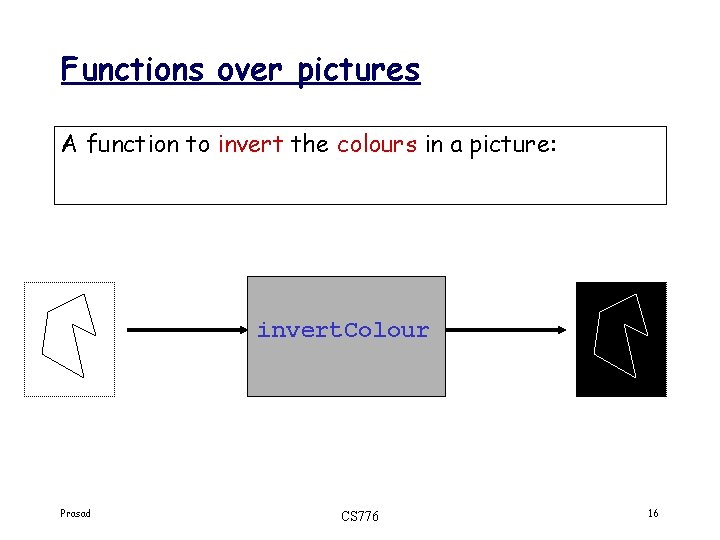
Functions over pictures A function to invert the colours in a picture: invert. Colour Prasad CS 776 16

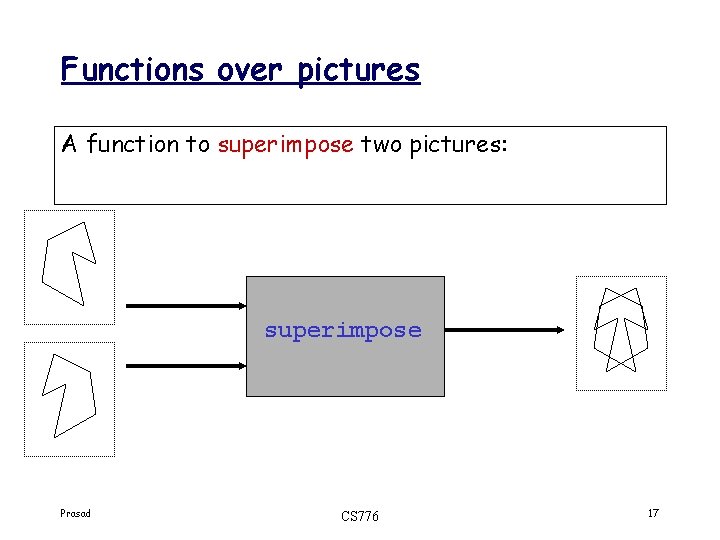
Functions over pictures A function to superimpose two pictures: superimpose Prasad CS 776 17

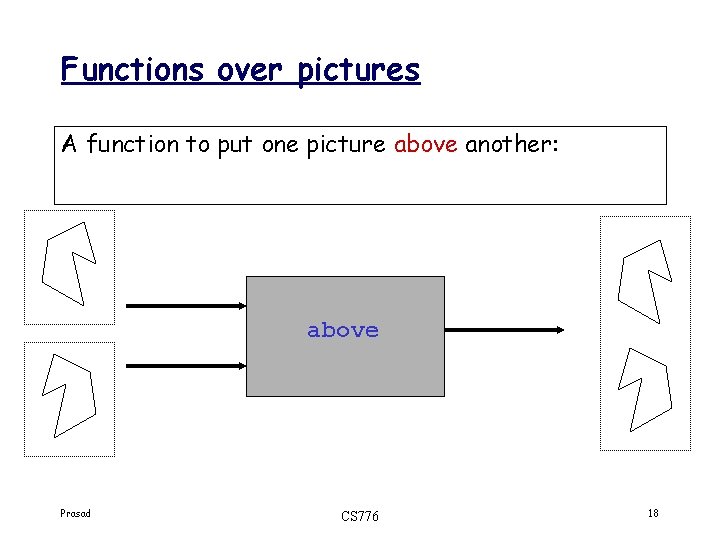
Functions over pictures A function to put one picture above another: above Prasad CS 776 18

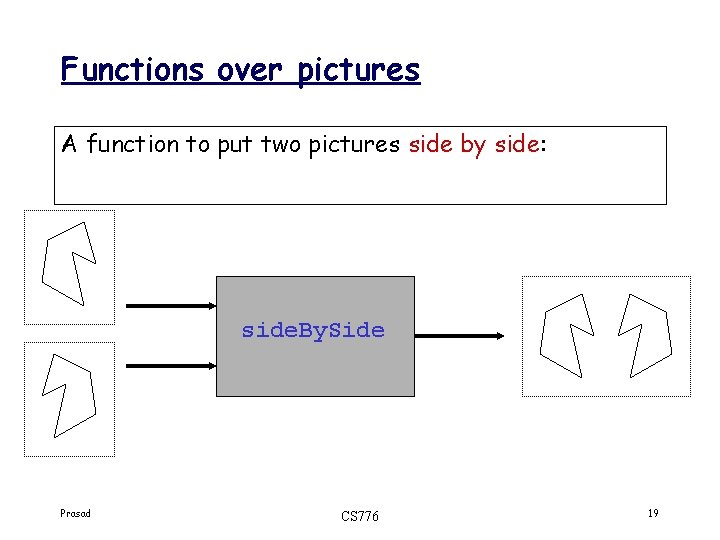
Functions over pictures A function to put two pictures side by side: side. By. Side Prasad CS 776 19

A naïve implementation type Picture = [String] type String = [Char] A Picture is a list of Strings. A String is a list of Char (acters). . . . ##. . . ###. #. . . . ##. . . . . #. #. . ##. . Prasad CS 776 20

How are they implemented? flip. H Reverse the list of strings. flip. V Reverse each string. rotate above flip. H then flip. V (or v. versa). Join the two lists of strings. side. By. Side Join corresponding lines. invert. Colour Change each Char … and each line. superimpose Join each Char … join each line. Prasad CS 776 21

How are they implemented? flip. H reverse flip. V map reverse rotate flip. V. flip. H above ++ side. By. Side zip. With (++) invert. Colour map (map invert. Char) superimpose zip. With (zip. With combine) Prasad CS 776 22

Lists and types Haskell is strongly typed: detect all type errors before evaluation. For each type t there is a type [t], 'list of t'. reverse [] = [] reverse (x: xs) = reverse xs ++ [x] reverse : : [a] -> [a] a is a type variable: reverse works over any list type, returning a list of the same type. Prasad CS 776 23

Flipping in a vertical mirror flip. V : : Picture -> Picture flip. V [] = [] flip. V (x: xs) = reverse x : flip. V xs Run along the list, applying reverse to each element Run along the list, applying … to every element. General pattern of computation. Prasad CS 776 24

Implementing the mapping pattern map f [] = [] map f (x: xs) = f x : map f xs map : : (a -> b) -> [a] -> [b] Examples over pictures: flip. V pic = map reverse pic invert. Colour pic = map invert. Line pic invert. Line line = map invert. Char line Prasad CS 776 25

Functions as data Haskell allows you to pass functions as arguments and return functions as results, put them into lists, etc. In contrast, in Pascal and C, you can only pass named functions, not functions you build dynamically. map is. Even = ? ? map is. Even : : [Int] -> [Bool] It is a partial application, which gives a function: give it a [Int] and it will give you back a [Bool] Prasad CS 776 26

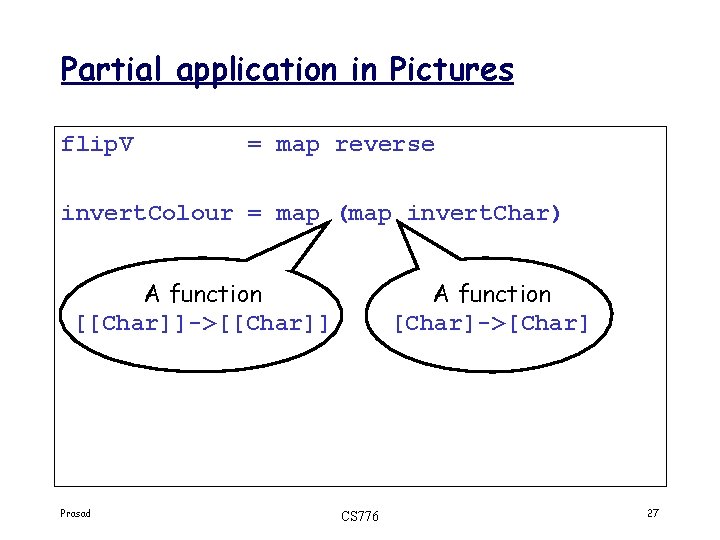
Partial application in Pictures flip. V = map reverse invert. Colour = map (map invert. Char) A function [[Char]]->[[Char]] Prasad A function [Char]->[Char] CS 776 27

Another pattern: zipping together side. By. Side [l 1, l 2, l 3] [r 1, r 2, r 3] = [ l 1++r 1, l 2++r 2, l 3++r 3 ] zip. With f (x: xs) (y: ys) = f x y : zip. With f xs ys = [] zip. With : : (a->b->c) -> [a] -> [b] -> [c] Prasad CS 776 28

In the case study … side. By. Side = zip. With (++) Superimposing two pictures: need to combine individual elements: combine : : Char -> Char combine top btm = if (top=='. ' && btm=='. ') then '. ' else '#' superimpose = zip. With (zip. With combine) Prasad CS 776 29

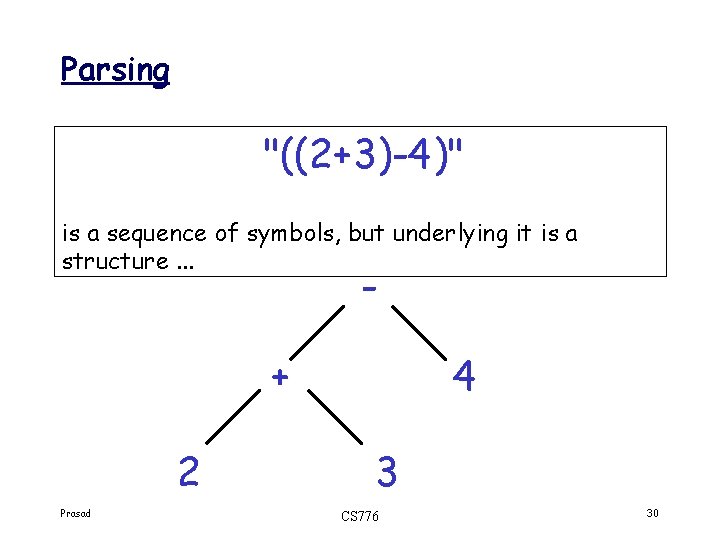
Parsing "((2+3)-4)" is a sequence of symbols, but underlying it is a structure. . . - + 2 Prasad 4 3 CS 776 30

Arithmetical expressions An expression is either • a literal, such as 234 or a composite expression: • the sum of two expressions (e 1+e 2) • the difference of two expressions (e 1 -e 2) • the product of two expressions (e 1*e 2) Prasad CS 776 31

How to represent these structures? data Expr = Lit Int | Sum Expr | Minus Expr | Times Expr Elements of this algebraic data type include Lit 34 34 Sum (Lit 45) (Lit 3) (45+3) Minus (Sum (Lit 2) (Lit 3)) (Lit 4) ((2+3)-4) Prasad CS 776 32

Counting operators data Expr = Lit Int | Sum Expr | Minus. . . How many operators in an expression? Definition using pattern matching c. Ops (Lit n) = 0 c. Ops (Sum e 1 e 2) = c. Ops e 1 + c. Ops e 2 + 1 c. Ops (Minus e 1 e 2) = c. Ops e 1 + c. Ops e 2 + 1 c. Ops (Times e 1 e 2) = c. Ops e 1 + c. Ops e 2 + 1 Prasad CS 776 33

Evaluating expressions data Expr = Lit Int | Sum Expr | Minus. . . Literals are themselves … eval (Lit n) = n … in other cases, evaluate the two arguments and then combine the results … eval (Sum e 1 e 2) = eval e 1 + eval e 2 eval (Minus e 1 e 2) = eval e 1 - eval e 2 eval (Times e 1 e 2) = eval e 1 * eval e 2 Prasad CS 776 34

List comprehensions Example list x = [4, 3, 2, 5] [ n+2 | n<-x, is. Even n] run through the n in x … 4 3 2 5 select those which are even … 4 2 and add 2 to each of them 6 4 giving the result [6, 4] Prasad CS 776 35

List comprehensions Example lists x = [4, 3, 2] y = [12, 17] [ n+m | n<-x, m<-y] run through the n in x … 4 3 2 and for each, run through the m in y … 12 17 20 14 19 add corresponding pairs 16 21 15 giving the result [16, 21, 15, 20, 14, 19] Prasad CS 776 36

Quicksort qsort [] = [] qsort (x: xs) = qsort elts_lt_x ++ [x] ++ qsort elts_greq_x where elts_lt_x = [y | y <- xs, y < x] elts_greq_x = [y | y <- xs, y >= x] Prasad CS 776 37

Merge. Sort merge. Sort [] = [] merge. Sort [x] = [x] merge. Sort xs | size >= 1 = merge (merge. Sort front) (merge. Sort back) where size = length xs `div` 2 front = take size xs back = drop size xs Prasad CS 776 38

Merging x x <= y? y merge [1, 3] [2, 4] 1 : merge [3] [2, 4] 1 : 2 : merge [3] [4] 1 : 2 : 3 : merge [] [4] Prasad 1 : 2 : 3 : [4] [1, 2, 3, 4] 39

Defining Merge One list gets smaller. merge (x : xs) (y : ys) | x <= y = x : merge xs (y : ys) | x > y = y : merge (x : xs) ys merge [] ys = ys merge xs [] = xs Prasad CS 776 Two possible base cases. 40

Lazy evaluation Only evaluate what is needed … infinite lists nums : : Int -> [Int] nums n = n : nums (n+1) sft (x: y: zs) = x+y sft (nums 3) = sft (3: nums 4) = sft (3: 4: nums 5) = 7 Prasad CS 776 41

The list of prime numbers primes = sieve (nums 2) sieve (x: xs) = x : sieve [ z | z<-xs, z `mod` x /= 0] To sieve (x: xs) return x, together with the result of sieveing xs with all multiples of x removed. Prasad CS 776 42