Functional Languages Why Referential Transparency Functions as first






![Evaluation • Bound Variables • lx. (x+y) • Substitution – M[x/N] – sub N Evaluation • Bound Variables • lx. (x+y) • Substitution – M[x/N] – sub N](https://slidetodoc.com/presentation_image/a09248878f8797a4d07adc2b74c36035/image-7.jpg)
![Evaluation (cont. ) • Beta Reduction – (lx. x+y)(z+w) – (lx. x+y)[x/(z+w)] – (z+w)+y Evaluation (cont. ) • Beta Reduction – (lx. x+y)(z+w) – (lx. x+y)[x/(z+w)] – (z+w)+y](https://slidetodoc.com/presentation_image/a09248878f8797a4d07adc2b74c36035/image-8.jpg)


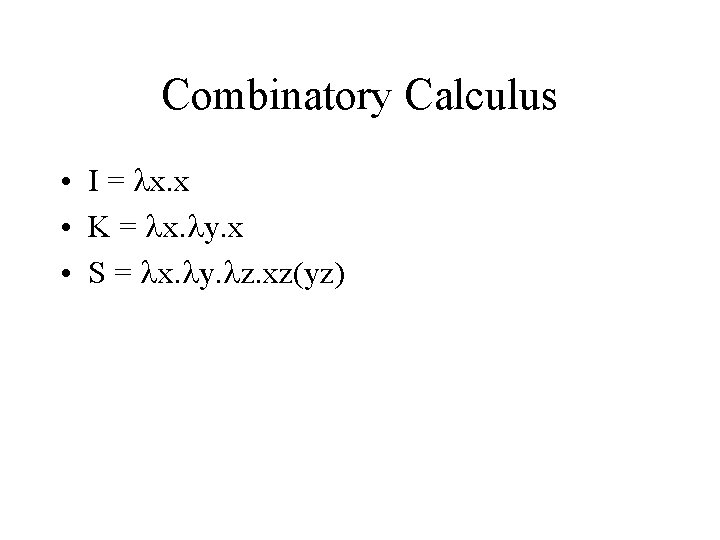





















- Slides: 33

Functional Languages

Why? • • Referential Transparency Functions as first class objects Higher level of abstraction Potential for parallel execution

History • LISP is one of the oldest languages (‘ 56’ 59)! • AI & John Mc. Carthy • Roots: – Church’s Lambda Calculus (Entscheidungsproblem!) – Church’s students

Functional Languages • LISP and its family – LISP, Common LISP, Scheme • • Haskell Miranda ML FP (John Backus)

Recent Events • Paul Graham – Hackers and Painters

Lambda Calculus • Abstract definition of functions lx. x*x Application: (lx. x*x)5 Multiple arguments lx. (ly. x*y)
![Evaluation Bound Variables lx xy Substitution MxN sub N Evaluation • Bound Variables • lx. (x+y) • Substitution – M[x/N] – sub N](https://slidetodoc.com/presentation_image/a09248878f8797a4d07adc2b74c36035/image-7.jpg)
Evaluation • Bound Variables • lx. (x+y) • Substitution – M[x/N] – sub N in for x in expression M – Valid when free variables in N are not bound in M – Variables can be renamed
![Evaluation cont Beta Reduction lx xyzw lx xyxzw zwy Evaluation (cont. ) • Beta Reduction – (lx. x+y)(z+w) – (lx. x+y)[x/(z+w)] – (z+w)+y](https://slidetodoc.com/presentation_image/a09248878f8797a4d07adc2b74c36035/image-8.jpg)
Evaluation (cont. ) • Beta Reduction – (lx. x+y)(z+w) – (lx. x+y)[x/(z+w)] – (z+w)+y

Two sides of the Lambda Calculus • The programming language side is what we have seen • Also – used for type systems • The theory side used to proof the Entscheidungsproblem

Defining Numbers • 0 = lf. lx. (x) • 1 = lf. lx. (fx) • 2 = lf. lx. (f(fx)) • Succ = ln. (lf. (lx. (f(n f) x))) • Add = lm. (ln. (lf. (lx. ((mf)((nf)x))))))
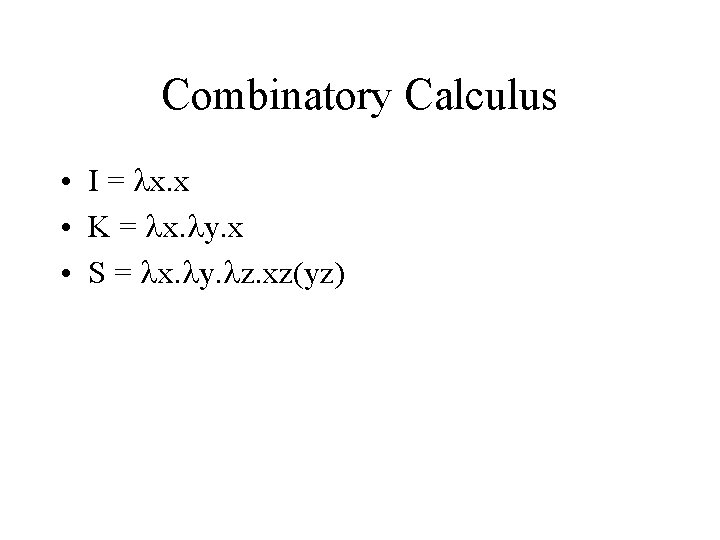
Combinatory Calculus • I = lx. x • K = lx. ly. x • S = lx. ly. lz. xz(yz)

Church-Rosser Theorem • Order of application and reduction does not matter!

LISP • Syntax – parenthesis! • Functions are written in prefix list form: – (add 4 5)

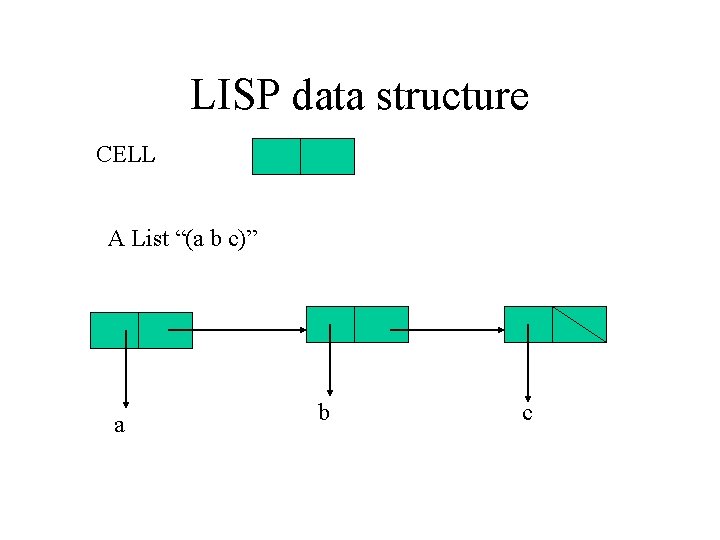
LISP data structure CELL A List “(a b c)” a b c

Evaluation • LISP assumes a list is a function unless evaluation is stopped! • (a b c) - apply function a to arguments b and c • Quote: ‘(a b c) – a list not to be evaluated

List Functions List Accessors car: (car ‘(a b c)) -> a cdr (cdr ‘(a b c)) -> (b c)

List Functions List constructors list (list ‘a ‘b) -> (a b) cons (cons ‘a ‘b) -> (a. b) What is happening here?

Symbolic Differentiation Example Pg 226

Haskell • Better syntax! • Named for Haskell Curry – a logician • 1999

Expressions • Use normal infix notation • Lists as a fundamental data type (most functional languages provide this) – Enumeration -> evens=[0, 2, 4, 6] – Generation -> • Moreevens = [ 2*x | x <- [0, 1. . 101]] – Construction • 8: [] – [8]

Expressions (cont. ) • List accessors – head and tail – head evens – 0 – tail evens – [2, 4, 6] • List concatenation – [1, 2] ++ [3, 4] – [1, 2, 3, 4]

Control Flow • If The Else statements • Functions: name : : Domain -> Range name <vars> | <s 1> | <s 2> ….

Example Function max 3 : : Int -> Int Max 3 x y z | x >=y && x >= z = x | y >= x && y >= z = y | otherwise = z

Recursion and Iteration • Recursion follows the obvious pattern • Iteration uses lists: – Fact n = product [1. . N] • Another pattern for recursion on lists – my. Sum [] = 0 – my. Sum [x : xs] = x + my. Sum[xs]

Implementation • Lazy evaluation • Eager evaluation • Graph reduction

SECD Machine • • • Four Data Structures (lists) S – stack, expression evaluation E – environment list of <id, value> C – control string (e. g. program) D – dump, the previous state for function return

Data types • Expr – – – ID(identifier) Lambda(identifier, expr) Application(expr 1, expr 2) @ (apply symbol) • WHNF – – INT(number) – Primary(WHNF -> WHNF) – Closure(expr, identifier, list( (identifier, WHNF)))

Data types (cont. ) • • Stack – list (WHNF) Environment – list ( <identifier, WHNF>) Control – list ( expr) Dump – list (<Stack, Environment, Control>) • State – – <Stack, Environment, Control, Dump>

Evaluate Function • Evaluate maps State -> WHNF • Cases for Control List empty: • Evaluate(Result: : S, E, nil) -> Result • Evaluate(x: : S, E, nil, (S 1, E 1, C 1)) -> Evaluate(x: : S 1, E 1, C 1, D)

Evaluate Function (cont. ) • Evaluate(S, E, ID(x): : C, D) -> Evaluate(Look. Up(x, E): : S, E, C, D) • Evaluate(S, E, LAMBDA(id, expr), D) -> Evaluate( Closure(expr, id, E 1): : S, E, C, D)

Evaluate Function (cont. ) • Evaluate(Closure(expr, id, E 1): : (arg: : S), E, @: : C, D) -> Evaluate(nil, (id, arg): : E 1, expr, (S, E, C): : D)

Evaluate Function (cont. ) • Evaluate(Primary(f): : (arg: : S), E, @: : C, D) -> Evaluate(f(arg): : S, E, C, D) • Evaluate(S, E, Application(fun, arg): : C, D) -> Evaluate(S, E, arg: : (fun: : (@: : C)), D)

Functional Programming • Little used in commercial circles • Used in some research circle • May hold the future for parallel computation