Functional Dependency for Verification Reduction Logic Minimization EE

Functional Dependency for Verification Reduction & Logic Minimization EE 290 N, Spring 2004 5/6/2004 J. -H. R. Jiang 1

Outline n n n Motivations Previous work Our formulation Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 2

Outline n n n Motivations Previous work Our formulation Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 3

Motivations n Logic synthesis of state transition systems n n Remove “redundant” registers using functional dependency Formal verification of state transition systems n 5/6/2004 Reduce state space and compact BDD representations by removing dependent state variables J. -H. R. Jiang 4

Outline n n Motivations Previous work n n n Functional dependency Signal correspondence Our formulation Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 5

Previous work n “Functional” dependency in state transition systems n Problem formulation n Solution – functional deduction n n Variable xi is redundant if and only if F|xi = 0 Æ F|xi = 1 = false Example n 5/6/2004 Given a characteristic function F(x 1, x 2, …, xn), compute a minimal set of irredundant (independent) variables Variable xi is redundant if it can be replaced with a function over other variables F = abc Ç : a: c Minimal independent sets: {a, b}, {b, c} with dependency functions c : = a, a : = c, respectively J. -H. R. Jiang 6

Previous work n Applications of functional dependency n Synthesis n n Verification n Register minimization in hardware synthesis from HDL Minimization of BDDs of reached state sets Embed detection of functional dependency inside reachability analysis as an on-the-fly reduction Weakness n 5/6/2004 Need to perform reachability analysis to derive functional dependency (for applying functional deduction) J. -H. R. Jiang 7

Unsolved problem n How to detect functional dependency without or before computing reached state sets ? 5/6/2004 J. -H. R. Jiang 8

Previous work n Signal correspondence n Problem formulation n A signal correspondence C µ s £ s is an equivalence relation (in reachable state subspace) on the set s of state variables n (This definition includes only identical functions, it can be extended to also include complemented functions) n An effective solution n Compute the equivalence relation by iterative refinement of state variables n n Valid for an over-approximated reachable space Application of detecting signal correspondence n Make sequential equivalence checking more like combinational equivalence checking n 5/6/2004 Detect equivalent state variables J. -H. R. Jiang 9

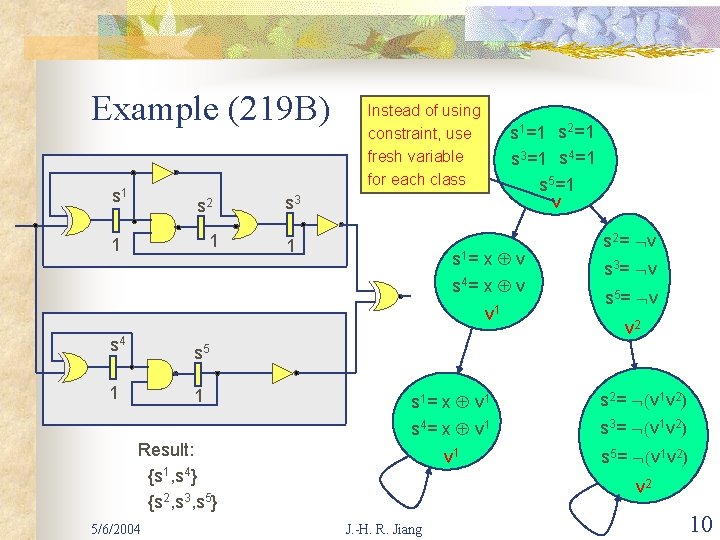
Example (219 B) s 1 s 2 1 1 Instead of using constraint, use fresh variable for each class s 1=1 s 2=1 s 3=1 s 4=1 s 5=1 v s 3 1 s 1= x Å v s 4= x Å v v 1 s 4 s 5 1 1 s 3= Øv s 5= Øv v 2 s 1= x Å v 1 s 4= x Å v 1 s 2= Ø(v 1 v 2) v 1 s 5= Ø(v 1 v 2) Result: {s 1, s 4} {s 2, s 3, s 5} 5/6/2004 s 2= Øv s 3= Ø(v 1 v 2) v 2 J. -H. R. Jiang 10

Previous work n Weakness n 5/6/2004 Signal correspondence is a very limited form of functional dependency J. -H. R. Jiang 11

Unsolved problem n How to characterize a more general form of functional dependency by fixed-point computation? 5/6/2004 J. -H. R. Jiang 12

Outline n n n Motivations Previous work Our formulation n Observation Combinational dependency Sequential dependency n n n Greatest fixed point Least fixed point Verification Reduction Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 13

Our formulation n Objective n n Resolve the unsolved problems (exploiting functional dependency and detecting signal correspondence) in a unified framework Key n Conclude functional dependency directly from transition functions of a state transition system. n n 5/6/2004 Define combinational dependency Extend to sequential dependency J. -H. R. Jiang 14

Combinational dependency n n Given two functions f and g over the same domain C, f functionally depends on g if there exists some function such that f (·) = ( g (·) ). A necessary and sufficient condition: f (a) f (b) g (a) g (b), for all a, b C In such case, we denote g v f n Consider multi-valued functions as vectors of Boolean functions 5/6/2004 J. -H. R. Jiang 15

Combinational dependency 5/6/2004 J. -H. R. Jiang 16

Combinational dependency 5/6/2004 J. -H. R. Jiang 17

Sequential dependency n n n Extend combinational dependency for state transition systems Find invariant such that sdep= (sind) and dep= ( ind) where s represents the set of state variable and represents the set of transition functions. Two approaches of computing fixed points n 5/6/2004 Greatest fixed-point (gfp); least fixed-point (lfp) J. -H. R. Jiang 18

Sequential dependency n Greatest fixed-point (gfp) computation n n 5/6/2004 Initially, all state variables are distinct. In each iteration, compute the combinational dependency among independent state variables from the previous iteration. J. -H. R. Jiang 19

Sequential dependency (gfp) 5/6/2004 J. -H. R. Jiang 20

Sequential dependency n Least fixed-point (lfp) computation n 5/6/2004 Initially, select one state var as the representative. (0) is determined by initial state information. In each iteration of computing functional dependency, try to reuse ’s from the previous iteration. If restrict ’s to be identity functions, the computation reduces to detecting signal correspondences. J. -H. R. Jiang 21

Sequential dependency (lfp) 5/6/2004 J. -H. R. Jiang 22

Legitimacy for logic synthesis n n Dependency may not hold for initial states which have no predecessors Localize conflicting state variables and declare them as independent state variables 5/6/2004 J. -H. R. Jiang 23

Verification reduction n Reachability analysis on reduced state space n Static verification reduction n n Dynamic (on-the-fly) verification reduction n n 5/6/2004 Before a reachability analysis, derive sequential dependency (using lfp or gfp computation). In each iteration of a reachability analysis, derive a minimal set of independent state variables before the image computation. (No need to try to reuse ’s. ) Thus, the image computation is over the reduced state space. Prior work on exploiting functional dependency is not effective because the detection of functional dependency is done after the image computation. J. -H. R. Jiang 24

Verification reduction 5/6/2004 J. -H. R. Jiang 25

Outline n n n Motivations Previous work Our formulation Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 26

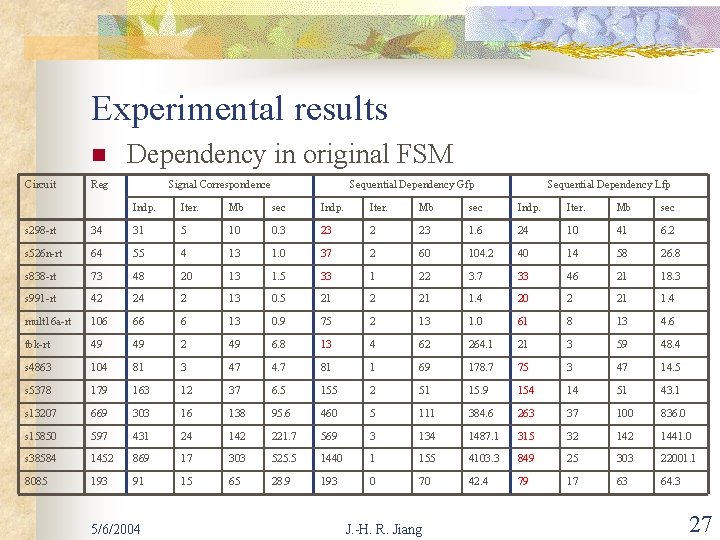
Experimental results n Circuit Dependency in original FSM Reg Signal Correspondence Sequential Dependency Gfp Sequential Dependency Lfp Indp. Iter. Mb sec s 298 -rt 34 31 5 10 0. 3 23 2 23 1. 6 24 10 41 6. 2 s 526 n-rt 64 55 4 13 1. 0 37 2 60 104. 2 40 14 58 26. 8 s 838 -rt 73 48 20 13 1. 5 33 1 22 3. 7 33 46 21 18. 3 s 991 -rt 42 24 2 13 0. 5 21 2 21 1. 4 20 2 21 1. 4 mult 16 a-rt 106 66 6 13 0. 9 75 2 13 1. 0 61 8 13 4. 6 tbk-rt 49 49 2 49 6. 8 13 4 62 264. 1 21 3 59 48. 4 s 4863 104 81 3 47 4. 7 81 1 69 178. 7 75 3 47 14. 5 s 5378 179 163 12 37 6. 5 155 2 51 15. 9 154 14 51 43. 1 s 13207 669 303 16 138 95. 6 460 5 111 384. 6 263 37 100 836. 0 s 15850 597 431 24 142 221. 7 569 3 134 1487. 1 315 32 1441. 0 s 38584 1452 869 17 303 525. 5 1440 1 155 4103. 3 849 25 303 22001. 1 8085 193 91 15 65 28. 9 193 0 70 42. 4 79 17 63 64. 3 5/6/2004 J. -H. R. Jiang 27

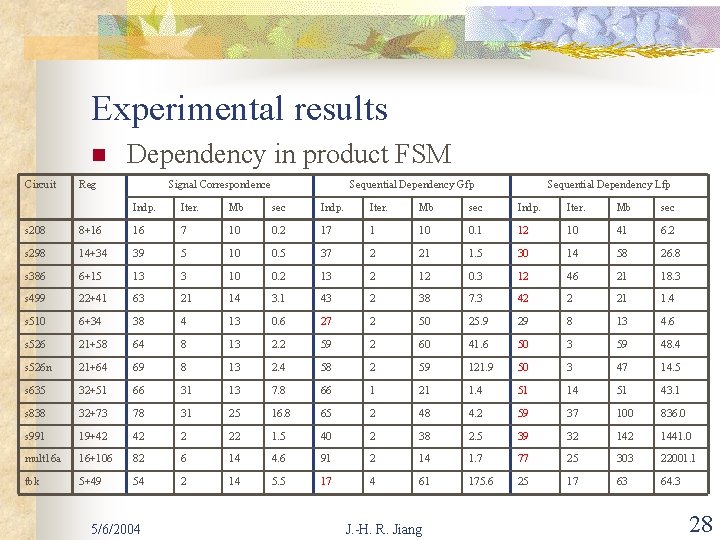
Experimental results n Circuit Dependency in product FSM Reg Signal Correspondence Sequential Dependency Gfp Sequential Dependency Lfp Indp. Iter. Mb sec s 208 8+16 16 7 10 0. 2 17 1 10 0. 1 12 10 41 6. 2 s 298 14+34 39 5 10 0. 5 37 2 21 1. 5 30 14 58 26. 8 s 386 6+15 13 3 10 0. 2 13 2 12 0. 3 12 46 21 18. 3 s 499 22+41 63 21 14 3. 1 43 2 38 7. 3 42 2 21 1. 4 s 510 6+34 38 4 13 0. 6 27 2 50 25. 9 29 8 13 4. 6 s 526 21+58 64 8 13 2. 2 59 2 60 41. 6 50 3 59 48. 4 s 526 n 21+64 69 8 13 2. 4 58 2 59 121. 9 50 3 47 14. 5 s 635 32+51 66 31 13 7. 8 66 1 21 1. 4 51 14 51 43. 1 s 838 32+73 78 31 25 16. 8 65 2 48 4. 2 59 37 100 836. 0 s 991 19+42 42 2 22 1. 5 40 2 38 2. 5 39 32 1441. 0 mult 16 a 16+106 82 6 14 4. 6 91 2 14 1. 7 77 25 303 22001. 1 tbk 5+49 54 2 14 5. 5 17 4 61 175. 6 25 17 63 64. 3 5/6/2004 J. -H. R. Jiang 28

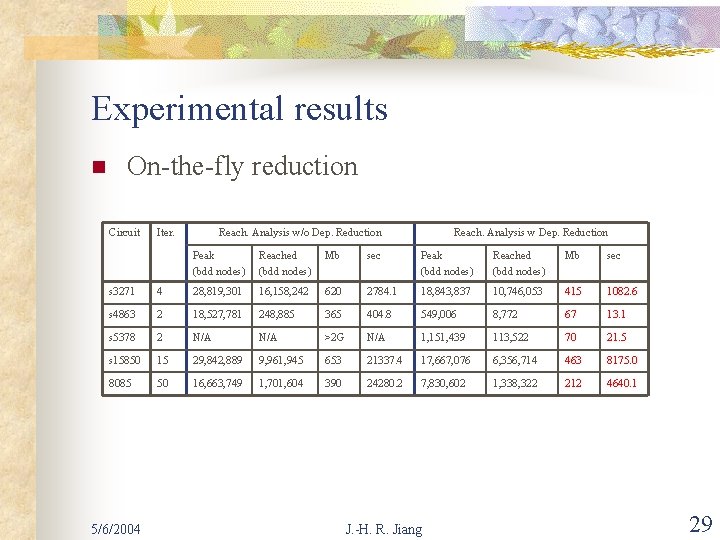
Experimental results n On-the-fly reduction Circuit Iter. Reach. Analysis w/o Dep. Reduction Reach. Analysis w Dep. Reduction Peak (bdd nodes) Reached (bdd nodes) Mb sec s 3271 4 28, 819, 301 16, 158, 242 620 2784. 1 18, 843, 837 10, 746, 053 415 1082. 6 s 4863 2 18, 527, 781 248, 885 365 404. 8 549, 006 8, 772 67 13. 1 s 5378 2 N/A >2 G N/A 1, 151, 439 113, 522 70 21. 5 s 15850 15 29, 842, 889 9, 961, 945 653 21337. 4 17, 667, 076 6, 356, 714 463 8175. 0 8085 50 16, 663, 749 1, 701, 604 390 24280. 2 7, 830, 602 1, 338, 322 212 4640. 1 5/6/2004 J. -H. R. Jiang 29

Outline n n n Motivations Previous work Our formulation Experimental results Conclusions 5/6/2004 J. -H. R. Jiang 30

Conclusions n n Proposed a computation of functional dependency w/o reachability analysis. Unified two previously independent studies on detecting signal correspondence and exploiting functional dependency. n n n Detecting signal correspondence is a special case of lfp computation of sequential dependency. Previous approach on exploiting functional dependency can be improved with our dynamic reduction. In addition to verification reduction, our results can be used to minimize state transition systems. 5/6/2004 J. -H. R. Jiang 31