Functional and Object Oriented Modeling of Mathematical Concepts

Functional and Object Oriented Modeling of Mathematical Concepts Shuichi YUKITA Hosei University

Contents • Functional View of Convergence – Cauchy’s Revolution • OO View of Convergence • Continuous Maps and Topology • Data Structures of Topology • Algorithms for Concrete Topology 2

Convergence of a sequence Cauchy’s Revolution in 1821 3

Example of convergence 4

Continuity of a function by Cauchy with Functional Presentation 5

Functional Proof • Functional proofs consist of the construction of functions and checking of the properties of the functions. • Computer Scientists feel comfortable when the problems are given in the language of data structures and algorithms. • Functional proofs make CS people happy explicitly, while mathematicians appreciate the goodness of functional approach implicitly. 6

A Proposition with a Functional Proof 7

A Proposition with a Functional Proof 8

Continuity of a function by Cauchy with Object Oriented Presentation 9

Object Oriented Proof 10

Topology Modern Approach to Continuity 11

Topology Modern Approach to Continuity 12

Continuity and Topology 13

Data Structures and Algorithms 14

Trivial Topology and Discrete Topology on the set {1, 2, 3} 15

A Topology on the set {1, 2, 3} 1 2 3 16

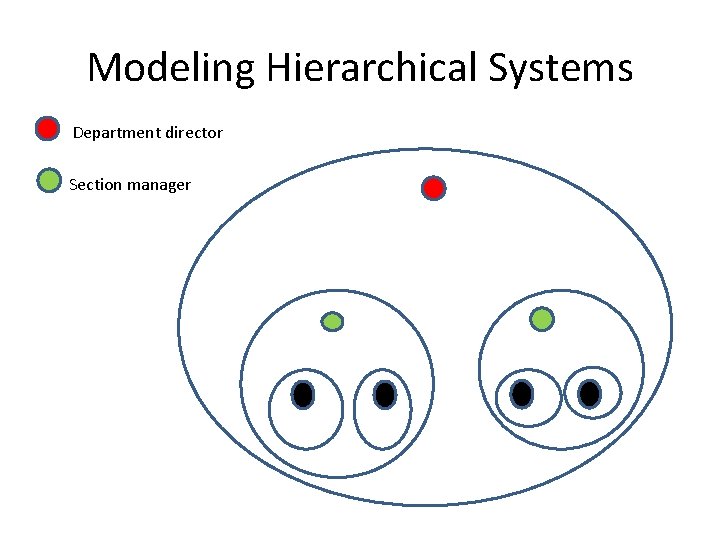
Modeling Hierarchical Systems Department director Section manager

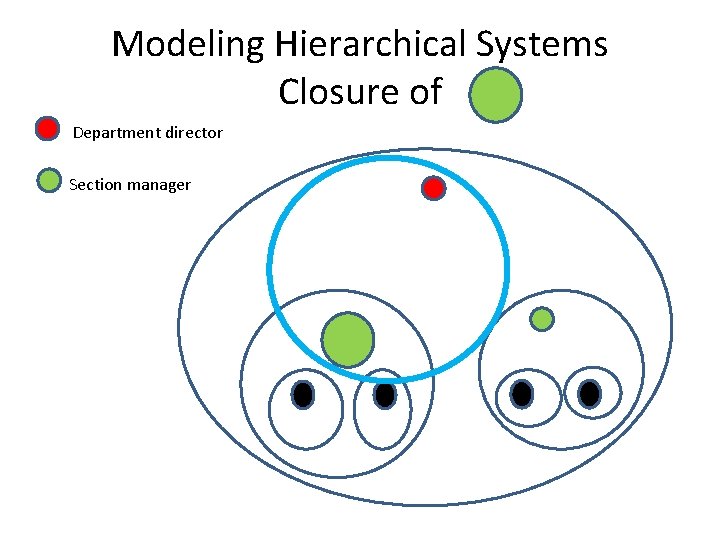
Modeling Hierarchical Systems Closure of Department director Section manager

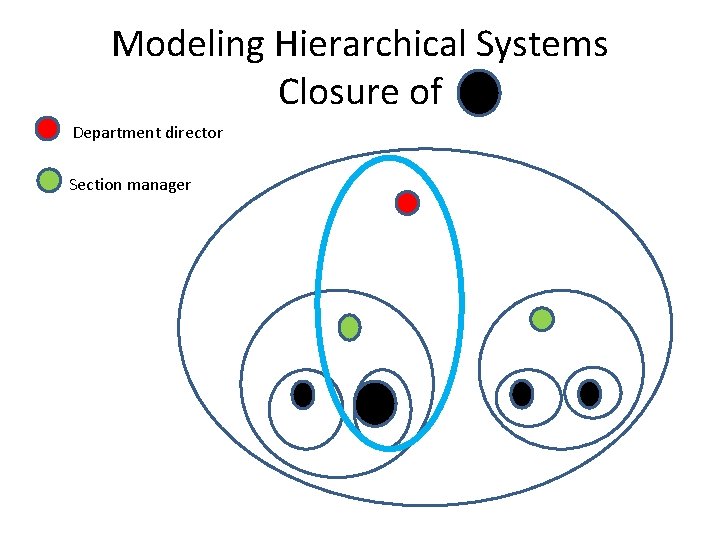
Modeling Hierarchical Systems Closure of Department director Section manager

Open Maps and Closed Maps 20

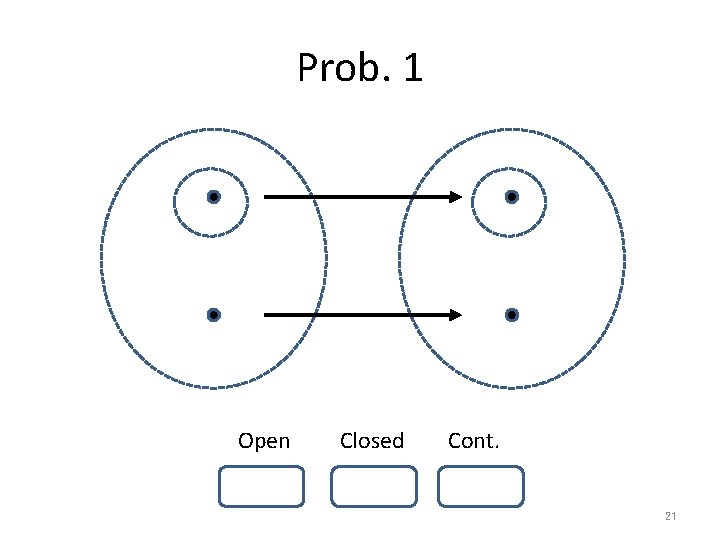
Prob. 1 Open Closed Cont. 21

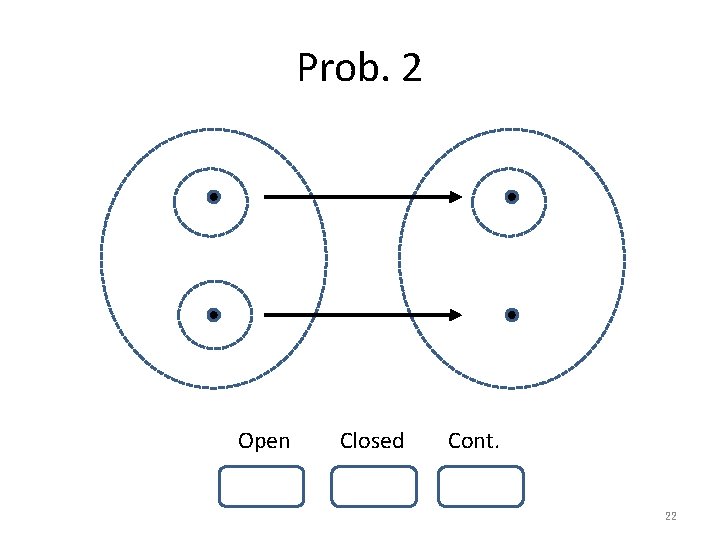
Prob. 2 Open Closed Cont. 22

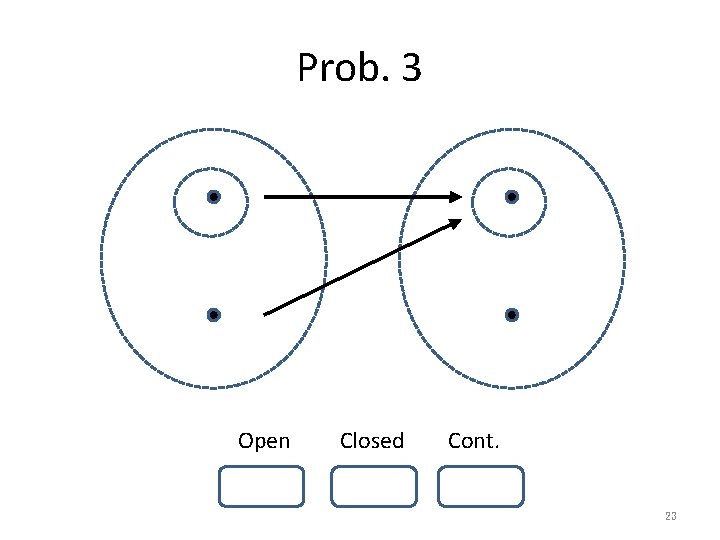
Prob. 3 Open Closed Cont. 23

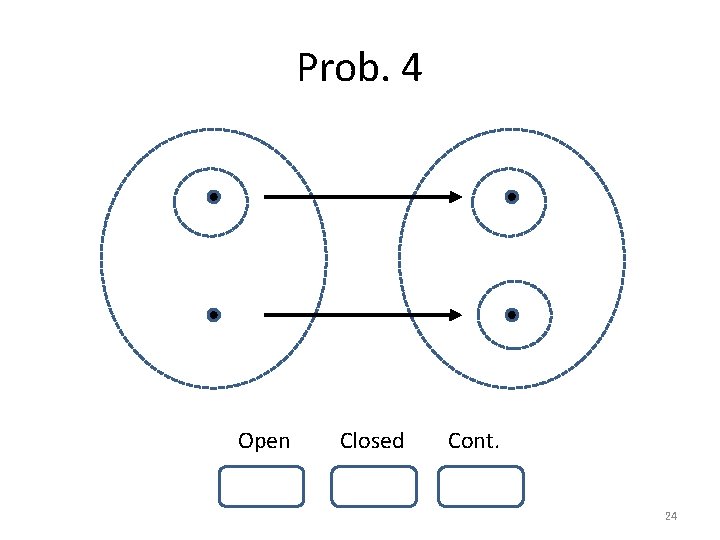
Prob. 4 Open Closed Cont. 24

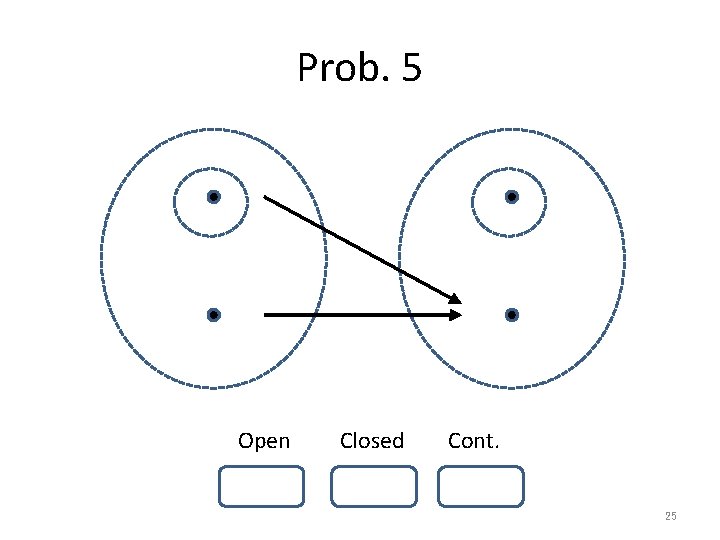
Prob. 5 Open Closed Cont. 25

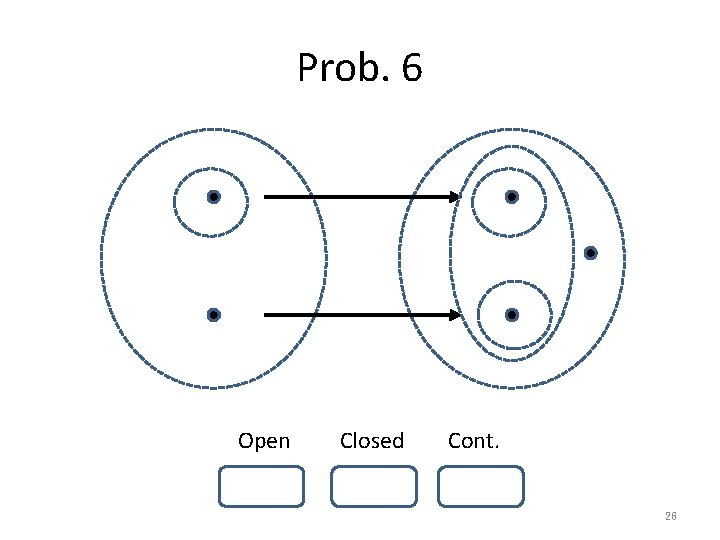
Prob. 6 Open Closed Cont. 26

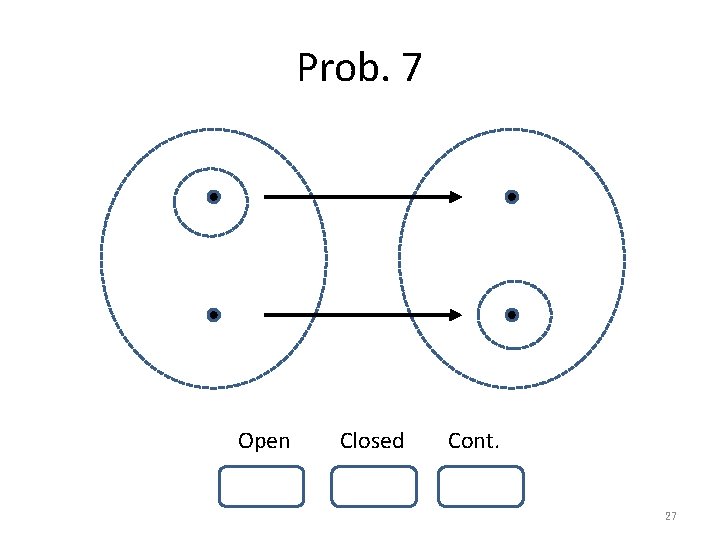
Prob. 7 Open Closed Cont. 27

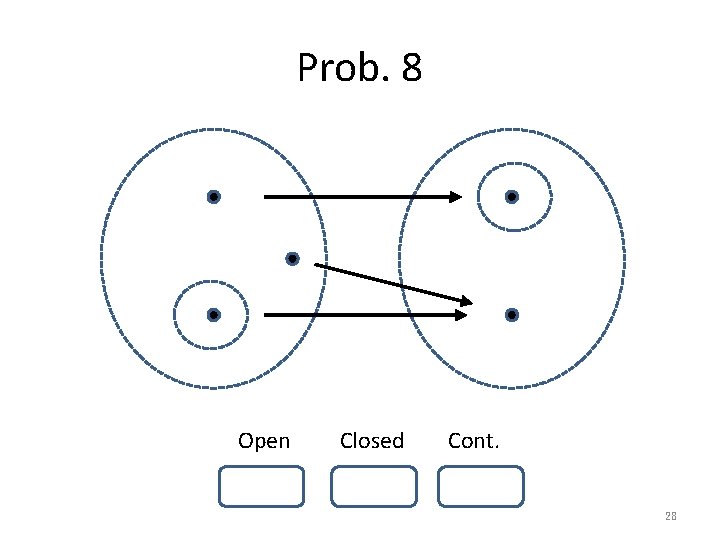
Prob. 8 Open Closed Cont. 28

References [1] S. Yukita, A Functional Presentation of Fourier Series Convergence, TVC vol. 12, no. 7 , pp. 350 -359, 1996. [2] A. J. Sieradski, “An Introduction to Topology and Homotopy, ” PWS-KENT Publishing Company, Boston. 29