Function Calls in MIPS To call a function

Function Calls in MIPS § To call a function: jal func — jal has a side-effect: it sets $ra to address of instruction after jal § To return from a function: jr § Calling conventions: — arguments “passed” in registers $a 0, …, $a 3 — return values in registers $v 0, $v 1 — callee can destroy: $t 0 -$t 9 $a 0 -$a 3 $v 0 -$v 1 — callee assumes caller will need: $s 0 -$s 7 $ra § For MP 2: You will be writing a function (called from our main program), which also calls one of our functions — you must assume the worst! $ra 1

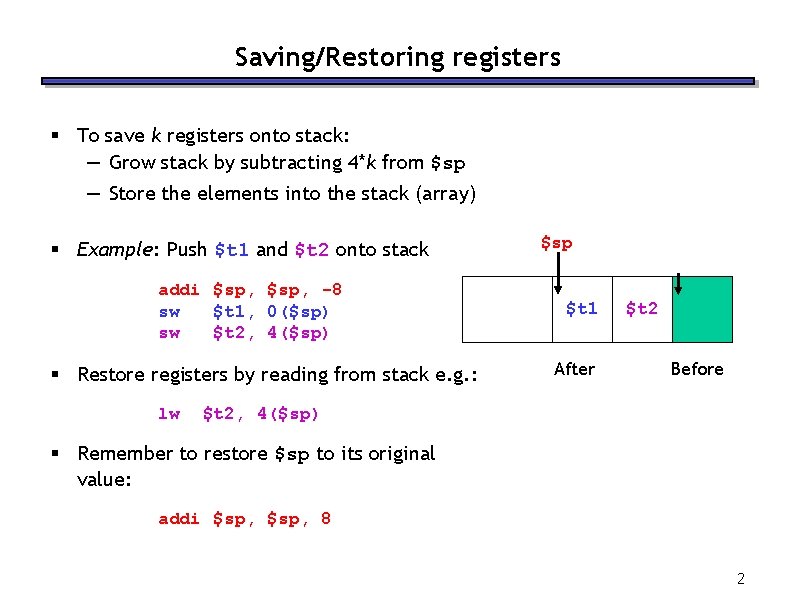
Saving/Restoring registers § To save k registers onto stack: — Grow stack by subtracting 4*k from $sp — Store the elements into the stack (array) § Example: Push $t 1 and $t 2 onto stack addi $sp, -8 sw $t 1, 0($sp) sw $t 2, 4($sp) § Restore registers by reading from stack e. g. : lw $sp $t 1 After $sp $t 2 Before $t 2, 4($sp) § Remember to restore $sp to its original value: addi $sp, 8 2

Finishing the main example § C++ code: if(func(7) == 7) func: # free to modify $a, $t and $v registers jr $ra main: li $a 0, 7 # set argument for call to func addi $sp, -8 # grow stack sw $a 0, 0($sp) # save $a 0 on stack sw $ra, 4($sp) # save $ra (jal modifies it) jal func # call func(7) lw $a 0, 0($sp) # restore $a 0 from stack lw $ra, 4($sp) addi $sp, 8 # shrink stack bne $a 0, $v 0, else. . . 3

Translate into MIPS int plus. One(int x) { return x + 1; } void main() { int x = 5; x += plus. One(x); } plus. One: # a 0 = x addi $v 0, $a 0, 1 jr $ra main: li addi sw sw jal lw lw addi add jr $a 0, 5 $sp, -8 $ra, 0($sp) $a 0, 4($sp) plus. One $ra, 0($sp) $a 0, 4($sp) $sp, 8 $a 0, $v 0 $ra 4

Recursive Functions § Recall that recursive functions have one or more base-cases, and one or more recursive calls. Example: int rec_max(int *array, int n) { if(n == 1) return array[0]; return max(array[n-1], rec_max(array, n-1)); } § Useful tip: Translate the base case first rec_max: # $a 0 = array = &array[0], $a 1 = n bne $a 1, 1, rec_case lw $v 0, 0($a 0) # return-value = array[0] jr $ra rec_case: . . . 5

The Recursive Case § Let’s examine the recursive step more carefully: return max(array[n-1], rec_max(array, n-1)); § Useful tip: Figure out what we need to remember across the recursive function call: array[n-1] (array, n-1) rec_case: addi $sp, -12 # save space for 3 regs addi $a 1, -1 # compute n-1 sw $a 0, 0($sp) # save &array[0] sw $a 1, 4($sp) # save n-1 sw $ra, 8($sp) # save $ra, since I’m doing jal! jal rec_max # recursive call with new args # restore $a 0, $a 1 and $ra # compare array[n-1] and $v 0, and put larger into $v 0 6

Translate into MIPS § Assume that the function print already exists void printrec(int *array, int n) { if(n > 1) { printrec: # a 0=array, a 1=n printrec(array, n/2); ble $a 1, 1, base_case. . . printrec(array+(n+1)/2, n/2); base_case: } addi $sp, -4 print(array[n/2]); sw $ra, 0($sp) } sll $a 1, 1 add lw jal lw addi jr $a 0, $a 1 $a 0, 0($a 0) print $ra, 0($sp) $sp, 4 $ra 7