FUNCIONES ELEMENTALES I CONTENIDOS MNIMOS Las funciones reales





























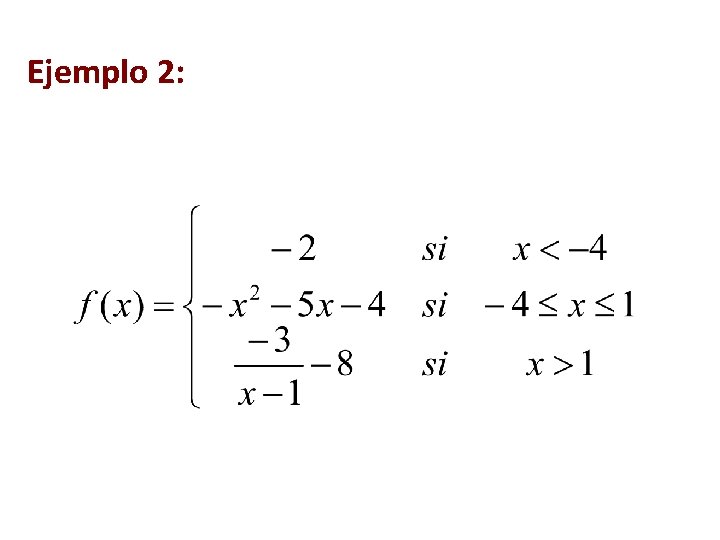





![G. FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación f(x)=E[x], que a G. FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación f(x)=E[x], que a](https://slidetodoc.com/presentation_image_h/0ea219ed97e88aba7e4282219c9e85eb/image-57.jpg)
![f(x)=E[x] f(x)=E[x]](https://slidetodoc.com/presentation_image_h/0ea219ed97e88aba7e4282219c9e85eb/image-58.jpg)

- Slides: 59

FUNCIONES ELEMENTALES I

CONTENIDOS MÍNIMOS • Las funciones reales de variable real. Gráfica y tabla de una función. • Descripción con la terminología adecuada de funciones dadas mediante sus gráficas: dominio, signo, cortes con los ejes, simetrías, periodicidad, tendencias, crecimiento, decrecimiento y extremos. • Utilización de tablas y gráficas funcionales para la interpretación de fenómenos sociales. • Obtención de valores desconocidos en funciones dadas por su tabla: interpolación y extrapolación lineal. Problemas de aplicación. • Características de las funciones polinómicas, raíz, exponencial, logarítmica, valor absoluto, parte entera y racionales sencillas, obtenidas a partir de la expresión analítica que las define. Las funciones definidas a trozos. • Utilización de las funciones como herramienta para la resolución de problemas relacionados con las ciencias sociales: financieros, de población, etc. , y para la interpretación de fenómenos sociales y económicos.

DEFINICIÓN DE FUNCIÓN • Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente, x, le corresponde un único valor de la variable dependiente, y • Recuerda que una función puede venir expresada como un enunciado: “gano 3€/hora”, una expresión algebraica: “y = 3 x”, una tabla de valores o una gráfica.

TIPOS DE FUNCIONES A. B. C. D. E. F. Funciones polinómicas Funciones racionales Funciones radicales Funciones definidas a trozos Función valor absoluto Función parte entera

ESTUDIO DE UNA FUNCIÓN • Hacer el estudio de una función consiste en analizar sus características


ESTUDIO DE UNA FUNCIÓN DOMINIO a partir de su expresión algebraica: Polinómica: Estas expresiones están definidas para todos los números reales: Domf = R. • Racional: Un cociente no está definido cuando el denominador es 0 • Irracional: Las raíces de índice par solo están definidas para radicandos positivos. • Logaritmos: solo están definidos para números reales positivos. • Razones trigonométricas de seno y coseno: siempre están definidas. • La tangente: no está definida cuando el coseno es cero. Además debes tener en cuenta: • El contesto real del que se ha extraído la función (ejemplo: • el área de un terreno) • Dónde ha sido definida la función (ejemplo: la recta y = 3 x – 8 definida en el intervalo x e (-1, 5] es un segmento rectilíneo)

A. FUNCIONES POLINÓMICAS. Función afín Estudio • Su gráfica es una línea recta: • m = pendiente • n = ordenada en el origen ( si n = 0 la recta pasa por el origen de coordenadas y se llama función lineal o de proporcionalidad directa) • Dominio: R • Recorrido: R si m no es 0 / n si m = 0 • Monotonía: • Si m > 0 la recta es creciente • Si m < 0 la recta es decreciente • Si m = 0 la recta es constante


A. FUNCIONES POLINÓMICAS. Función afín • Pendiente: aumento o disminución que se produce en la y cuando x aumenta unidad • Ecuación punto pendiente: • Gráfica: es suficiente con pintar dos puntos siendo uno de ellos la ordenada en el origen

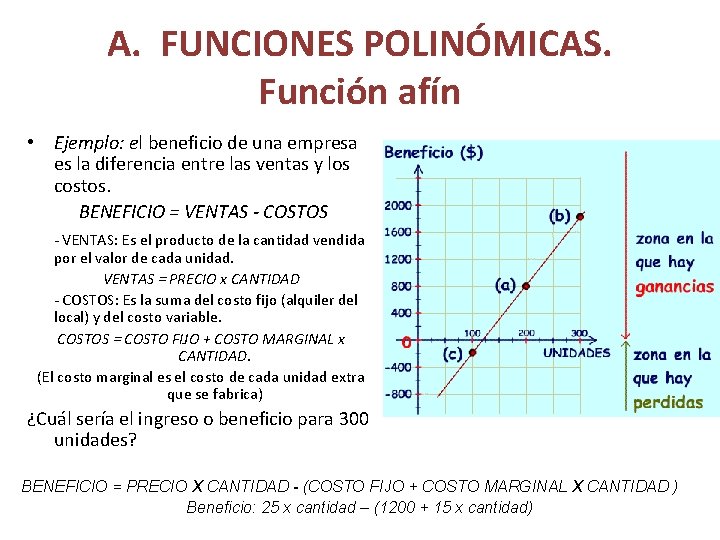
A. FUNCIONES POLINÓMICAS. Función afín • Ejemplo: el beneficio de una empresa es la diferencia entre las ventas y los costos. BENEFICIO = VENTAS - COSTOS - VENTAS: Es el producto de la cantidad vendida por el valor de cada unidad. VENTAS = PRECIO x CANTIDAD - COSTOS: Es la suma del costo fijo (alquiler del local) y del costo variable. COSTOS = COSTO FIJO + COSTO MARGINAL x CANTIDAD. (El costo marginal es el costo de cada unidad extra que se fabrica) ¿Cuál sería el ingreso o beneficio para 300 unidades? BENEFICIO = PRECIO X CANTIDAD - (COSTO FIJO + COSTO MARGINAL X CANTIDAD ) Beneficio: 25 x cantidad – (1200 + 15 x cantidad)

A. FUNCIONES POLINÓMICAS. Función afín • Interpolación lineal: Si de una función conocemos solamente dos de sus puntos, es claro que nada o casi nada podremos decir de su comportamiento en otros puntos. Sin embargo, si pudiéramos suponer que entre esos dos puntos la función es lineal, podríamos hallar exacta o aproximadamente sus valores en puntos intermedios valiéndonos de la ecuación de una recta. Supongamos que la función que pasa por los puntos A(x 0, x 1), B(y 0, y 1) es lineal en el intervalo [x 0, x 1], entonces podemos hallar su valor para cualquier abscisa, x, de este intervalo:

A. FUNCIONES POLINÓMICAS. Función afín • Extrapolación lineal: x es exterior al intervalo [x 0, x 1]. En la extrapolación, cuanto mas alejado esté x del intervalo, menos fiable es el valor que obtenemos para f(x). Ejemplo: si colgamos de un muelle una pesa de 40 g, se estira hasta 12 mm. Y si colgamos una pesa de 60 g, se estira has 20 mm. a) ¿Cuál sería su longitud si colgáramos una pesa de 55 g? b) ¿Cuál sería su longitud si colgáramos una pesa de 100 g? (resultado razonable) c) ¿Y si la pesa fuera de 5 kg? (el muelle se deforma o se rompe. Es un disparate)

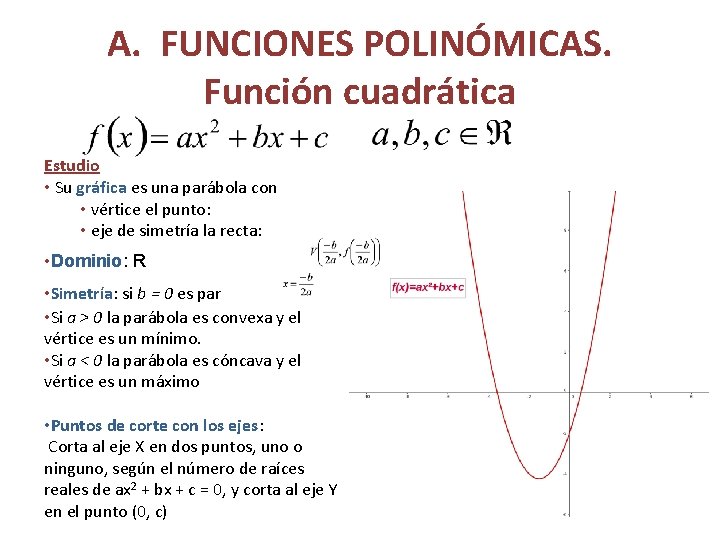
A. FUNCIONES POLINÓMICAS. Función cuadrática Estudio • Su gráfica es una parábola con • vértice el punto: • eje de simetría la recta: • Dominio: R • Simetría: si b = 0 es par • Si a > 0 la parábola es convexa y el vértice es un mínimo. • Si a < 0 la parábola es cóncava y el vértice es un máximo • Puntos de corte con los ejes: Corta al eje X en dos puntos, uno o ninguno, según el número de raíces reales de ax 2 + bx + c = 0, y corta al eje Y en el punto (0, c)



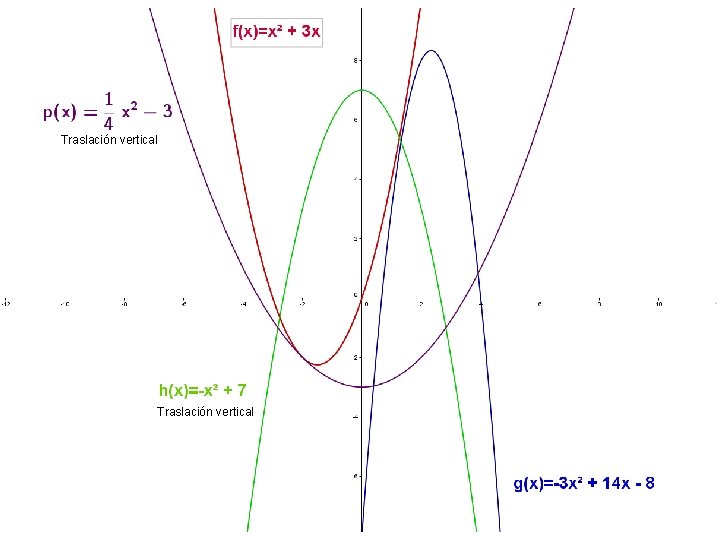
• A. FUNCIONES POLINÓMICAS. Función cuadrática Traslación vertical y = ax + c 2 La parábola y = ax 2 + c es una traslación vertical de c unidades de la parábola y = ax 2 -Si c > 0, la traslación es hacia arriba. -Si c < 0, la traslación es hacia abajo. • Traslación horizontal y = a(x – p)2 La parábola y = a(x – p)2 es una traslación horizontal de p unidades de la parábola y = ax 2 - El eje de simetría es la recta x = p - El vértice es el punto V(p, 0) • Traslación horizontal y vertical y = a(x – p)2 + k La parábola y = a(x – p)2 + k es una traslación horizontal de p unidades de la parábola y = ax 2 y una traslación vertical de k unidades, o viceversa. - El eje de simetría es la recta x = p - El vértice es el punto V(p, k)

Traslación vertical

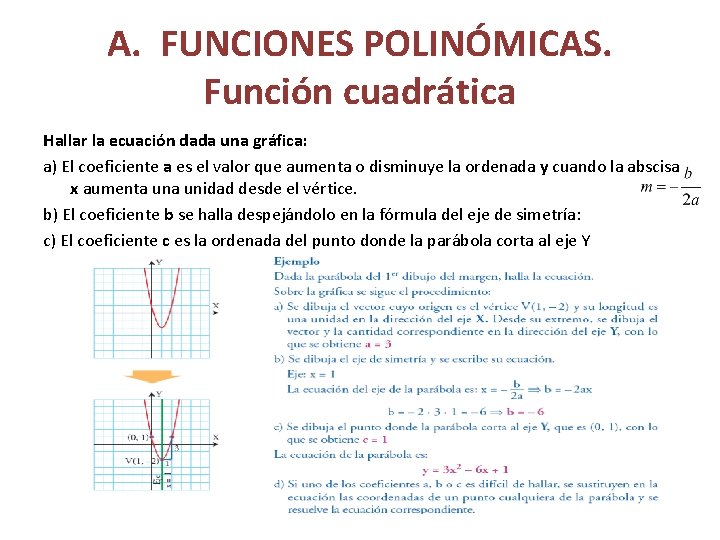
A. FUNCIONES POLINÓMICAS. Función cuadrática Hallar la ecuación dada una gráfica: a) El coeficiente a es el valor que aumenta o disminuye la ordenada y cuando la abscisa x aumenta unidad desde el vértice. b) El coeficiente b se halla despejándolo en la fórmula del eje de simetría: c) El coeficiente c es la ordenada del punto donde la parábola corta al eje Y

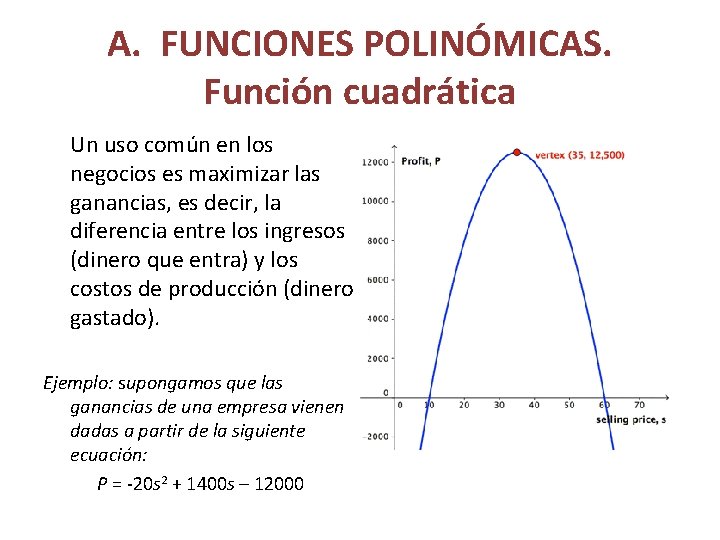
A. FUNCIONES POLINÓMICAS. Función cuadrática Un uso común en los negocios es maximizar las ganancias, es decir, la diferencia entre los ingresos (dinero que entra) y los costos de producción (dinero gastado). Ejemplo: supongamos que las ganancias de una empresa vienen dadas a partir de la siguiente ecuación: P = -20 s 2 + 1400 s – 12000

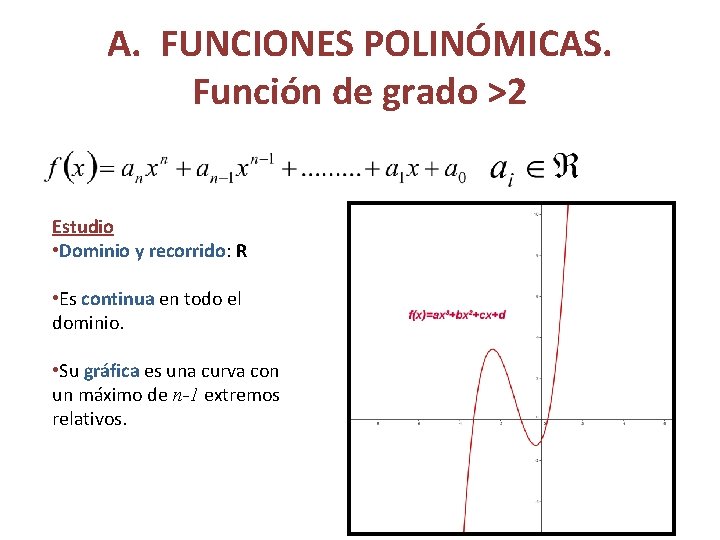
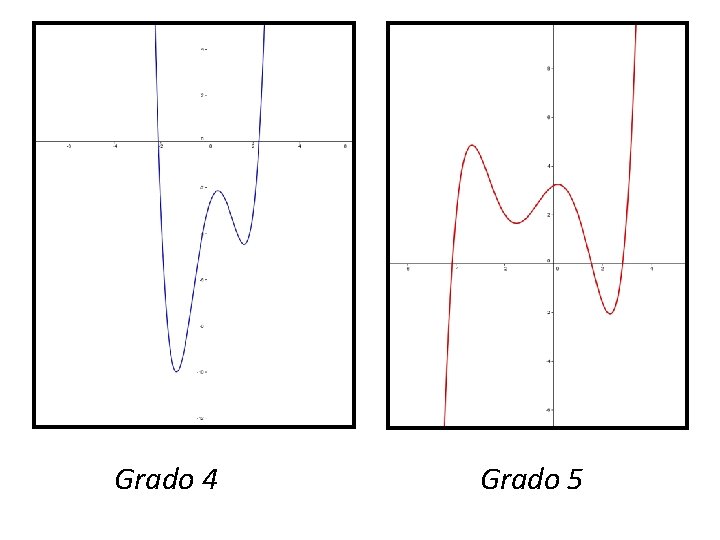
A. FUNCIONES POLINÓMICAS. Función de grado >2 Estudio • Dominio y recorrido: R • Es continua en todo el dominio. • Su gráfica es una curva con un máximo de n-1 extremos relativos.

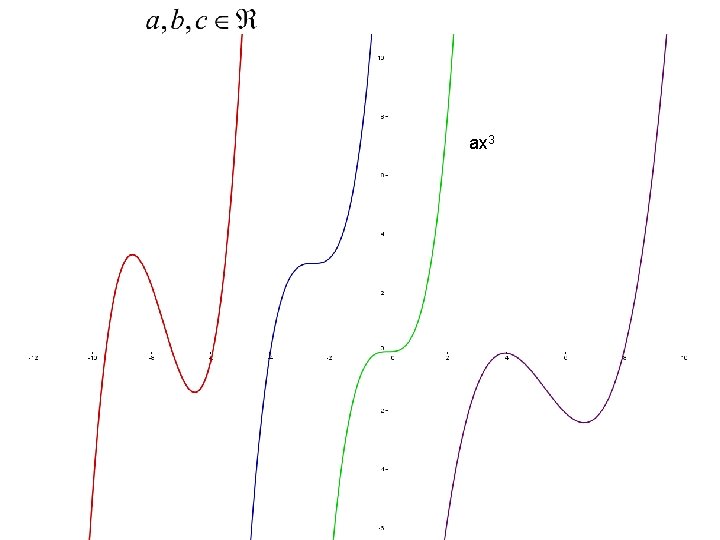
ax 3

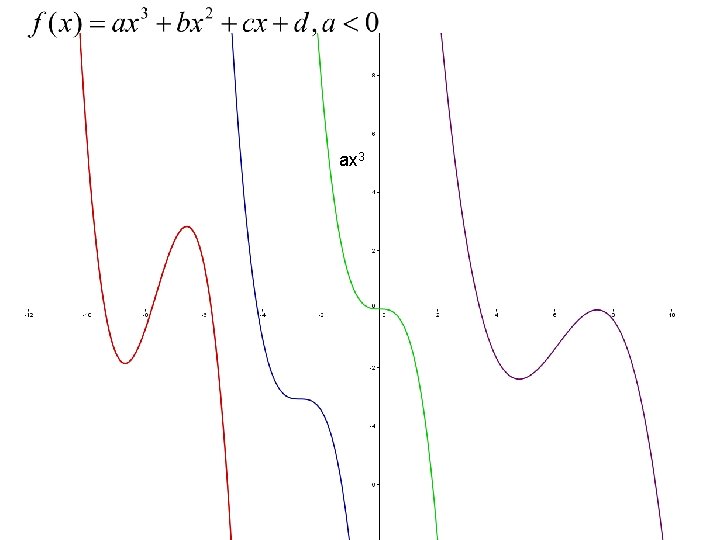
ax 3

Grado 4 Grado 5

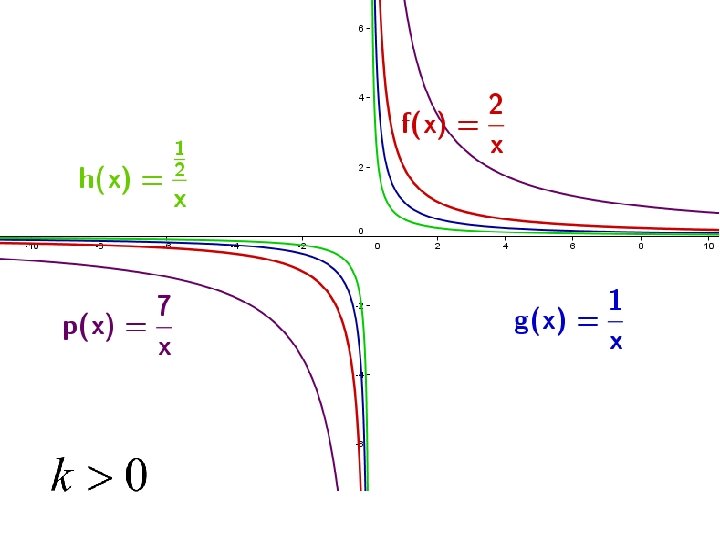
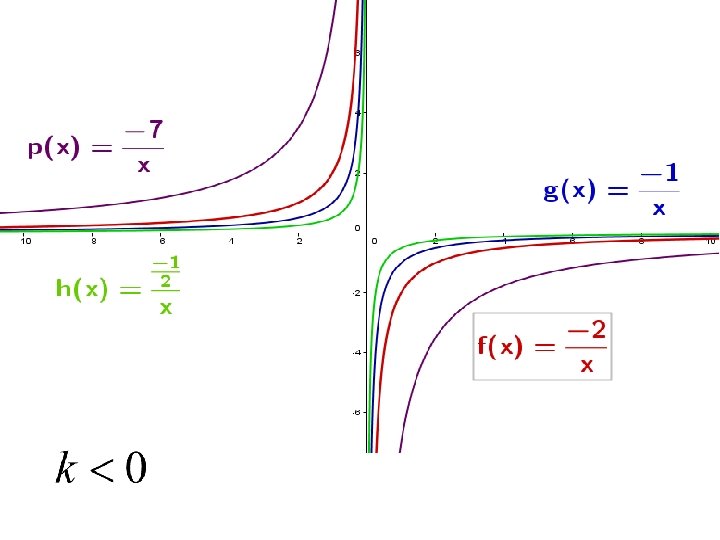
B. FUNCIONES RACIONALES Función de proporcionalidad inversa Estudio • Su gráfica es una hipérbola con asíntotas en los ejes de coordenadas. • Dominio: • Ramas: • Si k > 0 la hipérbola se sitúa en el primer y el tercer cuadrantes. Es decreciente en todo su dominio. • Si k < 0 la hipérbola se sitúa en el segundo y cuarto cuadrantes. Es creciente en todo su dominio. • Simetría: impar, respecto del origen de coordenadas



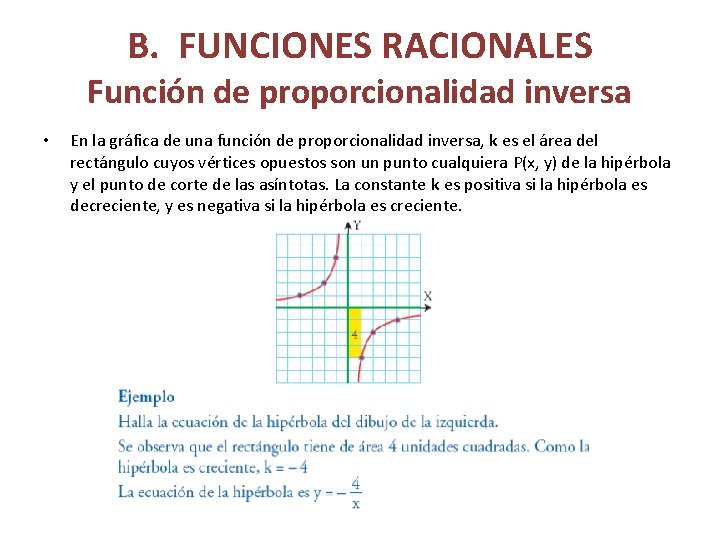
B. FUNCIONES RACIONALES Función de proporcionalidad inversa • En la gráfica de una función de proporcionalidad inversa, k es el área del rectángulo cuyos vértices opuestos son un punto cualquiera P(x, y) de la hipérbola y el punto de corte de las asíntotas. La constante k es positiva si la hipérbola es decreciente, y es negativa si la hipérbola es creciente.

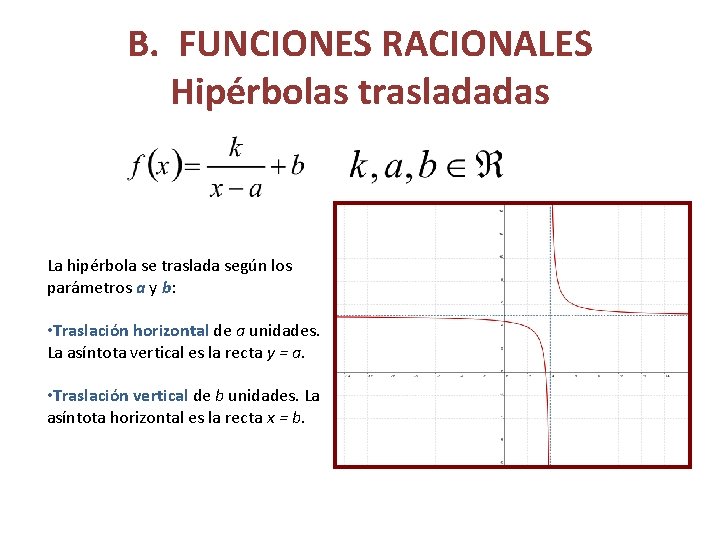
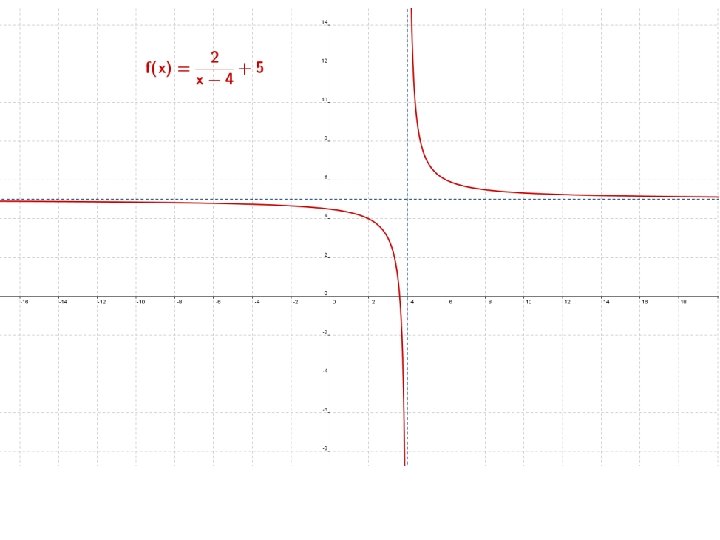
B. FUNCIONES RACIONALES Hipérbolas trasladadas La hipérbola se traslada según los parámetros a y b: • Traslación horizontal de a unidades. La asíntota vertical es la recta y = a. • Traslación vertical de b unidades. La asíntota horizontal es la recta x = b.


B. FUNCIONES RACIONALES

B. FUNCIONES RACIONALES Estudio • Dominio: • Asíntotas: en los ejes coordenados. • Ramas: • Si k > 0 la hipérbola se sitúa en el primer y el segundo cuadrantes. • Si k < 0 la hipérbola se sitúa en el tercer y el cuarto cuadrantes. • Simetría: Par, respecto del eje OY.


B. FUNCIONES RACIONALES General Estudio Dominio todos los números reales excepto aquellos en los que se anula el denominador, es decir, Q(x)=0. En esos puntos puede tener asíntotas verticales u oblicuas. Asíntotas: • Puede presentar una asíntota horizontal si el grado del numerador es menor o igual al denominador. • También tiene una asíntota oblicua si el grado del numerador es uno más que el denominador. Las posibles asíntotas verticales provienen de las raíces del denominador. Para un mejor estudio de las asíntotas es necesario el conocimiento de límites de funciones.



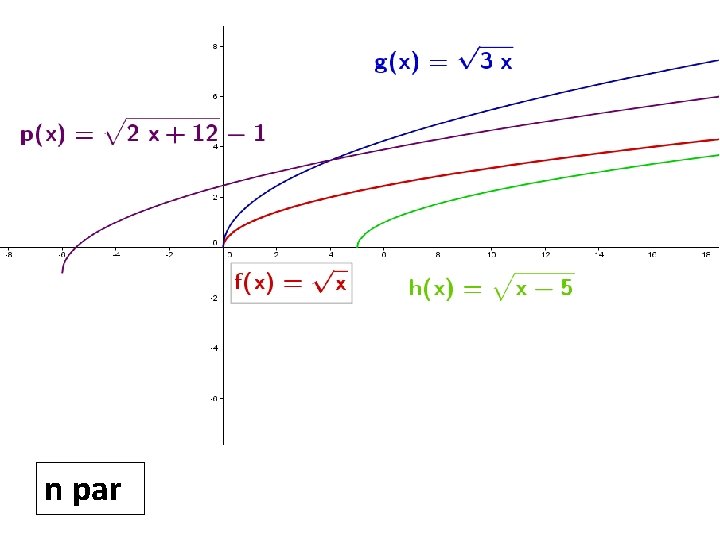
C. FUNCIONES RADICALES (funciones irracionales) Estudio • Dominio: • Si n es par: el intervalo en el que • Si n es impar: • Monotonía: Creciente en todo su dominio (Para que sea función consideramos solo uno de los resultados, el positivo o el negativo) El periodo de un péndulo T (tiempo de una oscilación) en función de su longitud l: T =

n par

n impar

RESUMEN TRANSFORMACIONES DE FUNCIONES • Representación de y = f(x) + k, y = f(x) – k es una traslación de f(x) hacia arriba o hacia abajo respectivamente. • Representación de y = -f(x) es la simétrica de f(x) respecto del eje X. • Representación de y = f(x + k), y = f(x + k) es una traslación a unidades hacia la derecha o hacia la izquierda. • Representación y = f(-x) es la simétrica de f(x) respecto del eje Y.

E. FUNCIONES DEFINIDAS A TROZOS Definición: “Una función definida a trozos es aquella cuyo dominio está dividido en intervalos disjuntos, de forma que en cada intervalo la función viene dada por expresiones matemáticas distintas”. Para dibujar las funciones a trozos tendremos que representar cada una de las partes de las que está compuesta teniendo en cuenta, además, que solo tienen validez en el intervalo en el que están definidas.

Ejemplo 1:

TRAMO I

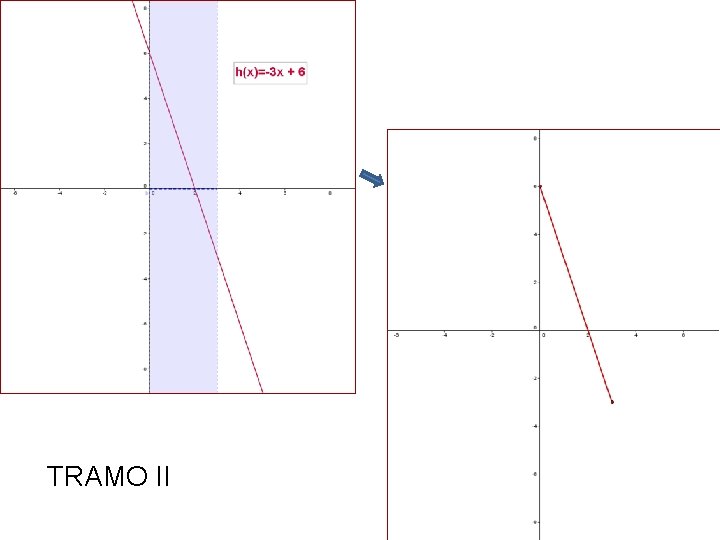
TRAMO II

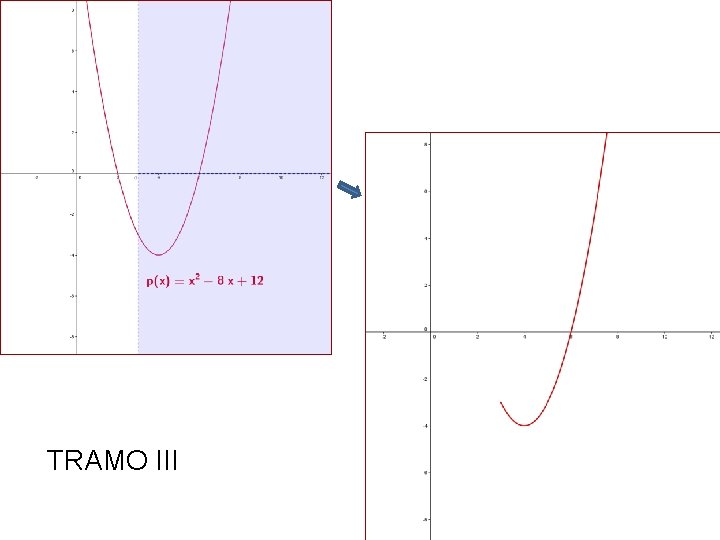
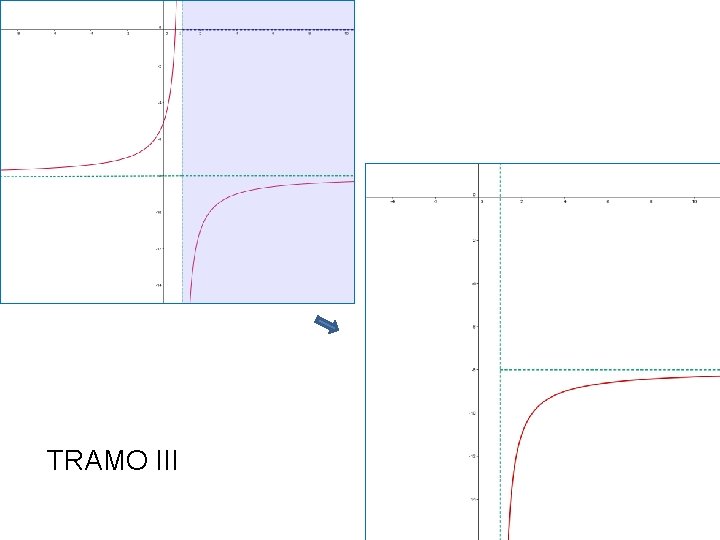
TRAMO III

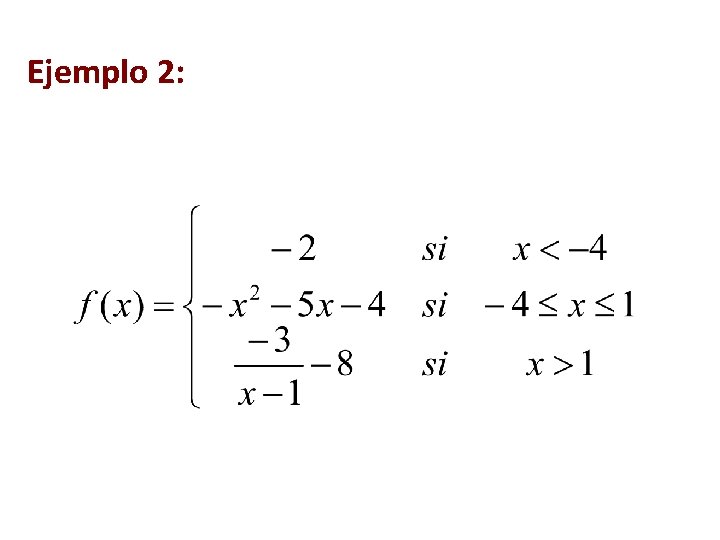
Ejemplo 2:

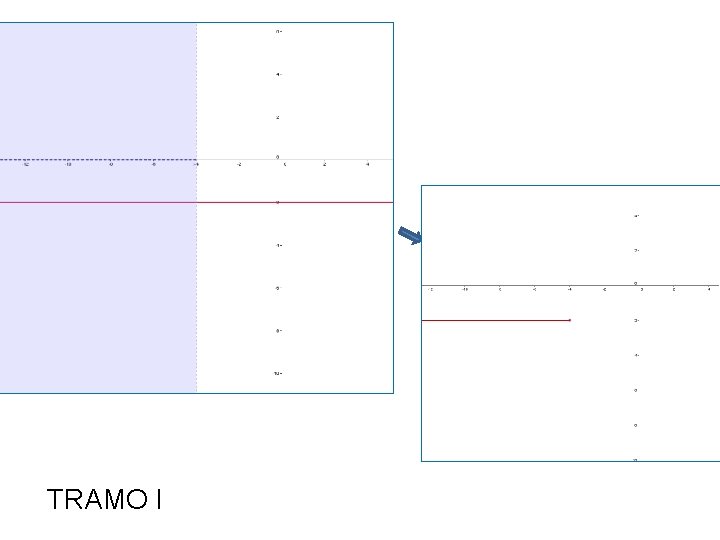
TRAMO I

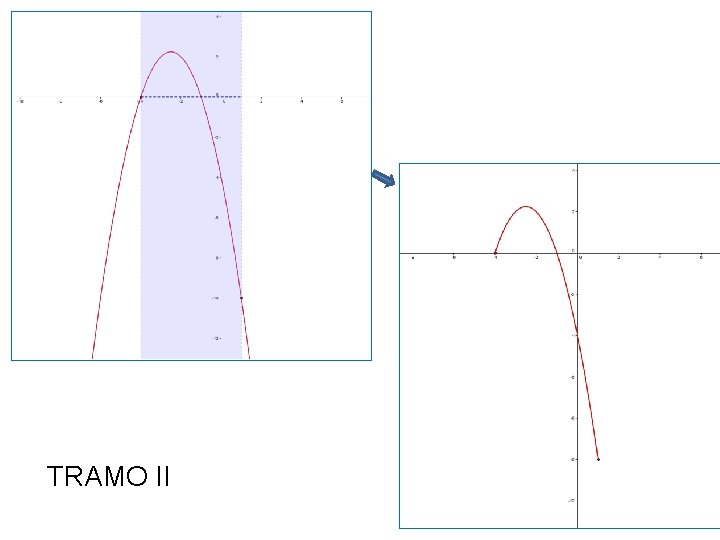
TRAMO II

TRAMO III


H. FUNCIÓN VALOR ABSOLUTO Se denomina así la función que a cada número real hace corresponder su valor absoluto. Se puede expresar también como una función definida a trozos Estudio • Recorrido: Puesto que el valor absoluto de un número es siempre positivo el recorrido de una función con valor absoluto estará incluido en los .


H. FUNCIÓN VALOR ABSOLUTO De un polinomio A trozos: Para establecer los intervalos en los que P(x) tiene signo negativo hay que resolver la ecuación P(x)=0 y estudiar el signo de P en cada uno de los intervalos en los queda dividida la recta real. Para dibujar su gráfica, se dibuja normalmente y después se hace la simetría respecto del eje horizontal en aquellos tramos en los que la función sea negativa.

Ejemplo Para expresar la función a trozos se buscan las raíces del polinomio P. Se estudia el signo de P en cada intervalo de la recta real.

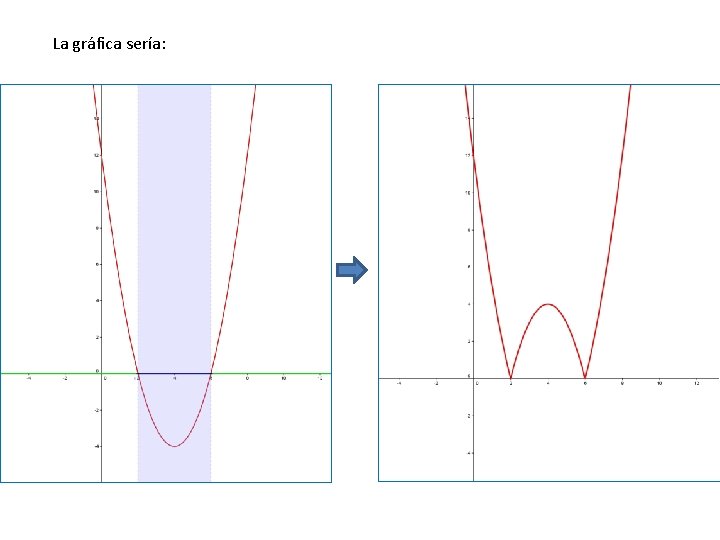
La gráfica sería:
![G FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación fxEx que a G. FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación f(x)=E[x], que a](https://slidetodoc.com/presentation_image_h/0ea219ed97e88aba7e4282219c9e85eb/image-57.jpg)
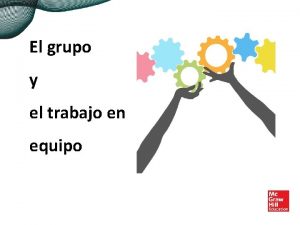
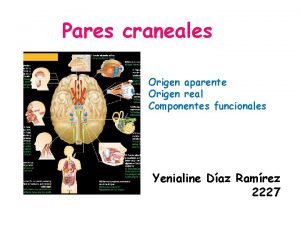
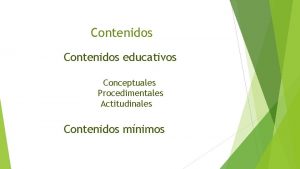
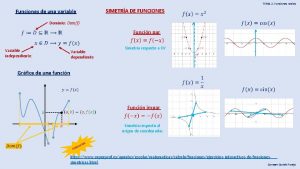
G. FUNCIÓN PARTE ENTERA Se denomina así la función de ecuación f(x)=E[x], que a cada número real hace corresponder el mayor número entero que es menor o igual que él. Se puede expresar también como una función definida a trozos
![fxEx f(x)=E[x]](https://slidetodoc.com/presentation_image_h/0ea219ed97e88aba7e4282219c9e85eb/image-58.jpg)
f(x)=E[x]

FUNCIÓN PARTE DECIMAL La parte decimal o mantisa de un número x es Mant(x) = x – Ent(x) • A partir de esto, definimos la función decimal de x, Mant(x), que hace corresponder a cada número x su parte decimal.
 Funciones reales ejemplos
Funciones reales ejemplos La pendiente
La pendiente Proposicion atomica
Proposicion atomica Operaciones elementales algoritmos
Operaciones elementales algoritmos Señales elementales
Señales elementales Elementales
Elementales Objetivos de los papeles de trabajo
Objetivos de los papeles de trabajo Principales funciones de la mitocondria
Principales funciones de la mitocondria Particulas elementales
Particulas elementales Las funciones de las palabras
Las funciones de las palabras Procedimental conceptual y actitudinal
Procedimental conceptual y actitudinal Ejemplos de contenidos actitudinales
Ejemplos de contenidos actitudinales Contenidos de aprendizaje.
Contenidos de aprendizaje. Indicadores de logro ejemplos
Indicadores de logro ejemplos Enfoque de conocimiento del medio segundo grado de primaria
Enfoque de conocimiento del medio segundo grado de primaria Objetivo actitudinal ejemplos
Objetivo actitudinal ejemplos S-nhyzk-bvg -site:youtube.com
S-nhyzk-bvg -site:youtube.com Secuenciación de contenidos
Secuenciación de contenidos Objetivos de repaso
Objetivos de repaso Contenidos desarrollados
Contenidos desarrollados Contenidos interdisciplinares
Contenidos interdisciplinares Texto expositivo esquema
Texto expositivo esquema Introduccion de un trabajo
Introduccion de un trabajo Fuentes reales del derecho
Fuentes reales del derecho Organizador grafico de numeros reales
Organizador grafico de numeros reales Elementos reales de un contrato
Elementos reales de un contrato Oraciones imaginarias y reales
Oraciones imaginarias y reales Oraciones imaginarias
Oraciones imaginarias Slidetodoc.com
Slidetodoc.com Ron basada
Ron basada Salmos reales
Salmos reales Parametros reales
Parametros reales Fuentes del derecho
Fuentes del derecho Elementos reales de un contrato
Elementos reales de un contrato El pianista hechos reales
El pianista hechos reales El cuento es una
El cuento es una Publicidad posesoria
Publicidad posesoria Contrato de reporto mercantil
Contrato de reporto mercantil Carta de compresibilidad generalizada termodinamica
Carta de compresibilidad generalizada termodinamica Raices complejas conjugadas+ecuaciones diferenciales
Raices complejas conjugadas+ecuaciones diferenciales Nervio olfatorio origen real
Nervio olfatorio origen real Diagrama representativo
Diagrama representativo Mercados reales
Mercados reales Fluidos ideales
Fluidos ideales Criterio del cociente series
Criterio del cociente series Tipos de opciones reales
Tipos de opciones reales Kamasutra posiciones reales
Kamasutra posiciones reales Extinción de derechos
Extinción de derechos Derechos reales administrativos ejemplos
Derechos reales administrativos ejemplos Numeros reales definicion
Numeros reales definicion Salmo primero
Salmo primero Estado financiero presupuestado
Estado financiero presupuestado Lri y lrs
Lri y lrs Es un arreglo rectangular de números reales
Es un arreglo rectangular de números reales Nmeros reales
Nmeros reales Vph flujo amarillo
Vph flujo amarillo Matriz del perfil competitivo
Matriz del perfil competitivo Obligaciones propter rem
Obligaciones propter rem Nmeros reales
Nmeros reales Division de reales
Division de reales