Funciones Calculo 1 Definicin de conjunto Un conjunto

Funciones Calculo 1

Definición de conjunto Un conjunto es una colección de objetos que cumplen con alguna propiedad. Los conjunto pueden especificarse de varias formas: a. Enumerando sus elementos entre llaves: {1, 2 , 3}, {2, 4, 6 , 8 , 10, …} b. Mediante una frase que especifique elementos contiene: el conjunto de los números pares. Se acostumbra utilizar la siguiente notación: {x | p(x) } Donde ”|” se lee “tal que” y p(x) es una proposición acerca de la variable x. {x | x es un número par} {x | x es un entero mayor que 0 y menor que 4} = {1, 2, 3} Un conjunto A es subconjunto de otro B sui todos los elementos de A también perteneces a B. Se denota por A B El conjunto vacío es aquel que no contiene elementos.

Conjuntos numéricos Número enteros: N = {…, -4. -3, -2, -1, 0 , 1, 2, 3, 4, …} Números racionales: Q = { x | x = p/q donde p y q N y q ≠ 0} Números irracionales: T = { x | x no puede expresarse como p/q donde p y q N y q ≠ 0} Números Reales: es la unión del conjunto de los racionales y los irracionales.

subconjunto Un conjunto A es subconjunto de otro conjunto B si todos los elementos de A también son elementos de B. A B a A b B El conjunto vacío es subconjunto de todos los conjuntos.

Cuantificadores Los cuantificadores se utilizan para indicar cuantos elementos de un conjunto cumplen con una propiedad. Cuantificador universal: x para todo x. Cuantificador existencial: x existe x. x A P(x) {x A | P(x) } = A x A P(x) {x A | P(x) } A B = { x | x A x B}

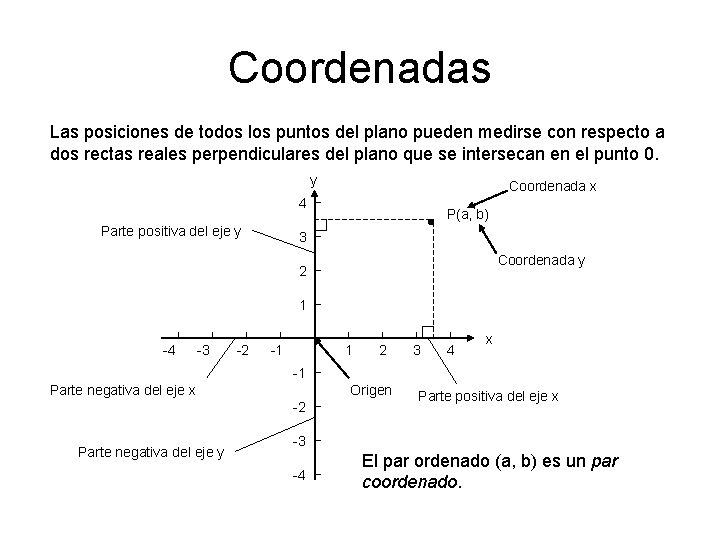
Coordenadas Las posiciones de todos los puntos del plano pueden medirse con respecto a dos rectas reales perpendiculares del plano que se intersecan en el punto 0. y Coordenada x 4 Parte positiva del eje y P(a, b) 3 Coordenada y 2 1 -4 -3 -2 -1 1 2 3 4 x -1 Parte negativa del eje x Origen -2 Parte negativa del eje y Parte positiva del eje x -3 -4 El par ordenado (a, b) es un par coordenado.

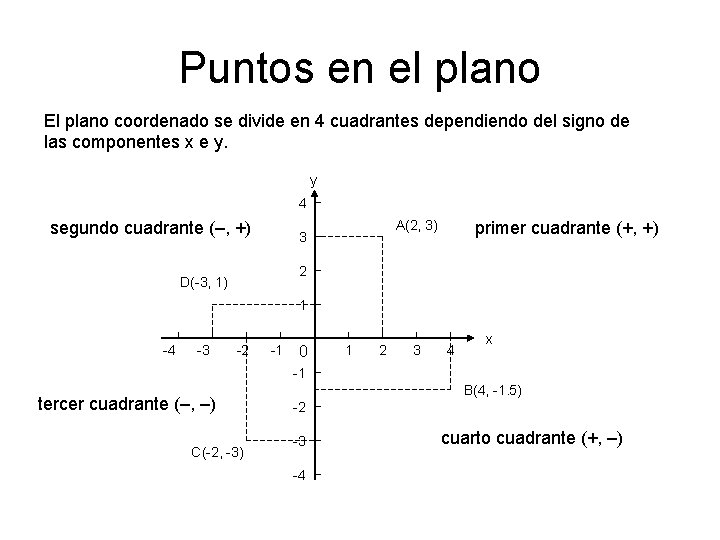
Puntos en el plano El plano coordenado se divide en 4 cuadrantes dependiendo del signo de las componentes x e y. y 4 segundo cuadrante (–, +) A(2, 3) 3 primer cuadrante (+, +) 2 D(-3, 1) 1 -4 -3 -2 -1 0 1 2 3 4 x -1 tercer cuadrante (–, –) C(-2, -3) B(4, -1. 5) -2 -3 -4 cuarto cuadrante (+, –)

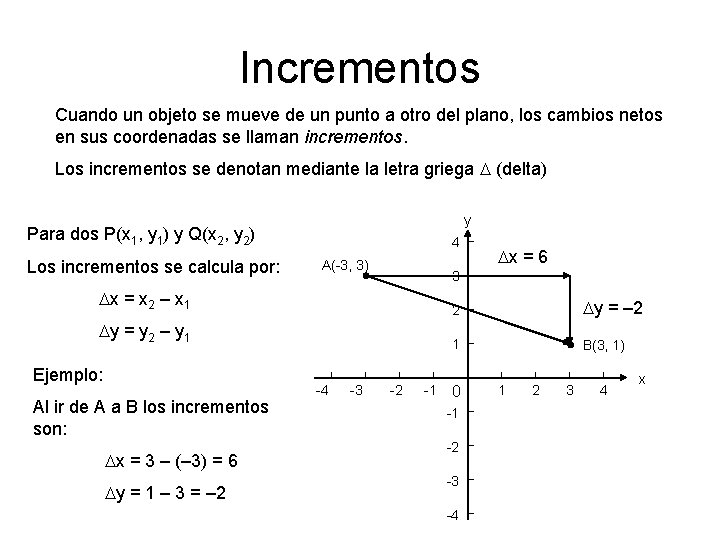
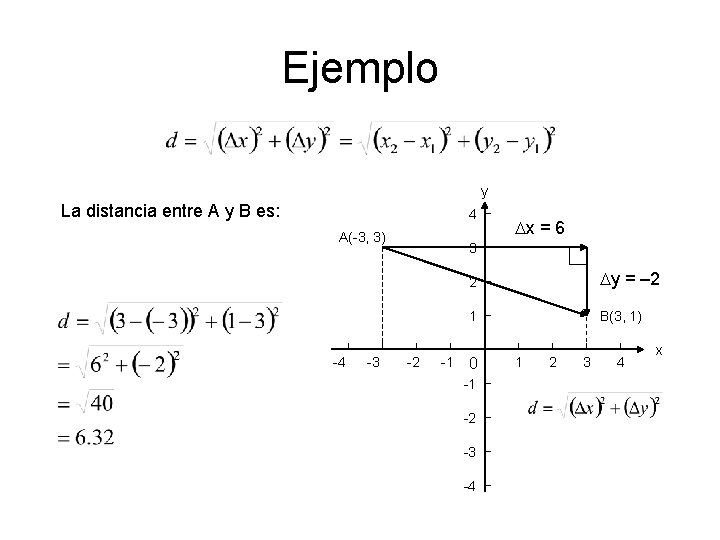
Incrementos Cuando un objeto se mueve de un punto a otro del plano, los cambios netos en sus coordenadas se llaman incrementos. Los incrementos se denotan mediante la letra griega D (delta) y Para dos P(x 1, y 1) y Q(x 2, y 2) Los incrementos se calcula por: 4 A(-3, 3) 3 Dx = x 2 – x 1 Dy = y 2 – y 1 Ejemplo: Al ir de A a B los incrementos son: Dx = 3 – (– 3) = 6 Dy = 1 – 3 = – 2 -4 -3 Dx = 6 -2 -1 2 Dy = – 2 1 B(3, 1) 0 -1 -2 -3 -4 1 2 3 4 x

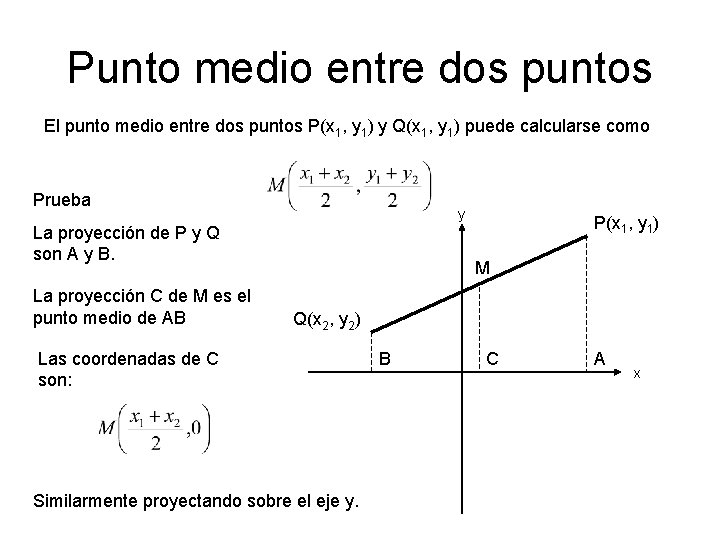
Punto medio entre dos puntos El punto medio entre dos puntos P(x 1, y 1) y Q(x 1, y 1) puede calcularse como Prueba y La proyección de P y Q son A y B. La proyección C de M es el punto medio de AB P(x 1, y 1) M Q(x 2, y 2) Las coordenadas de C son: Similarmente proyectando sobre el eje y. B C A x

Distancia entre dos puntos La distancia entre dos puntos P(x 1, y 1) y Q(x 2, y 2) se calcula por el teorema de Pitágoras y Prueba |PR| = | x 2 – x 1 | |RQ| = | y 2 – y 1 | Q(x 2, y 2) Por el teorema de Pitágoras |PQ|2 = | x 2 – x 1 |2 + | y 2 – y 1 |2 = (x 2 – x 1)2 + (y 2 – y 1)2 x P(x 1, y 1) R(x 2, y 1)

Ejemplo y La distancia entre A y B es: 4 A(-3, 3) -4 -3 Dx = 6 3 -2 -1 2 Dy = – 2 1 B(3, 1) 0 -1 -2 -3 -4 1 2 3 4 x

Tarea #3 Dibuje los siguientes puntos en el plano coordenado: P(– 4, 5), Q(3, – 4), R(3, 6), S(– 3, – 3) Encuentre y dibuje el punto medio entre el punto P y los puntos Q, R y S. Encuentre los incrementos en x y y al ir del punto P a los puntos Q, R y S. Encuentre la distancia entre P y los puntos Q, R y S.

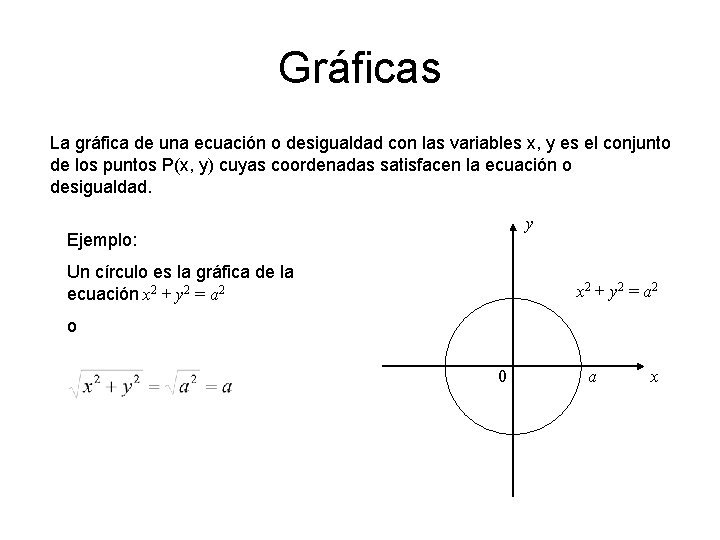
Gráficas La gráfica de una ecuación o desigualdad con las variables x, y es el conjunto de los puntos P(x, y) cuyas coordenadas satisfacen la ecuación o desigualdad. y Ejemplo: Un círculo es la gráfica de la ecuación x 2 + y 2 = a 2 o 0 a x

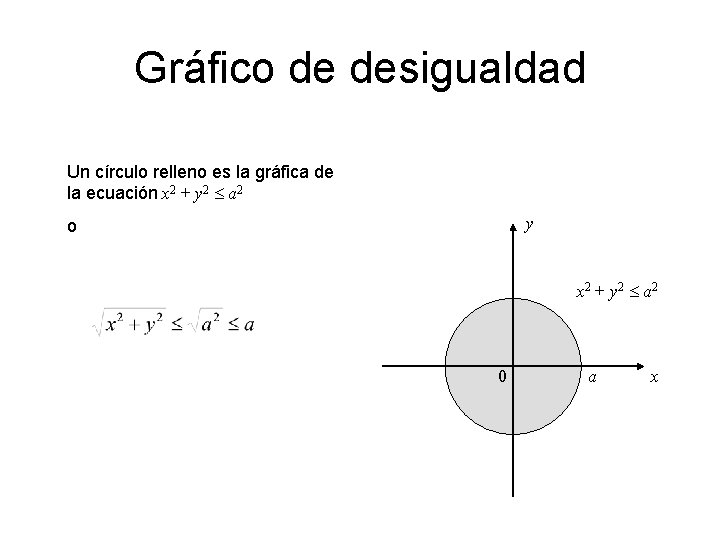
Gráfico de desigualdad Un círculo relleno es la gráfica de la ecuación x 2 + y 2 a 2 y o x 2 + y 2 a 2 0 a x

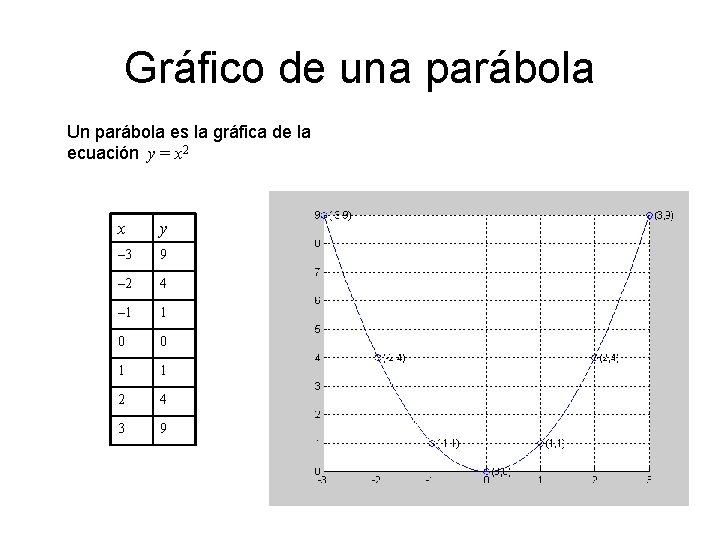
Gráfico de una parábola Un parábola es la gráfica de la ecuación y = x 2 x y – 3 9 – 2 4 – 1 1 0 0 1 1 2 4 3 9

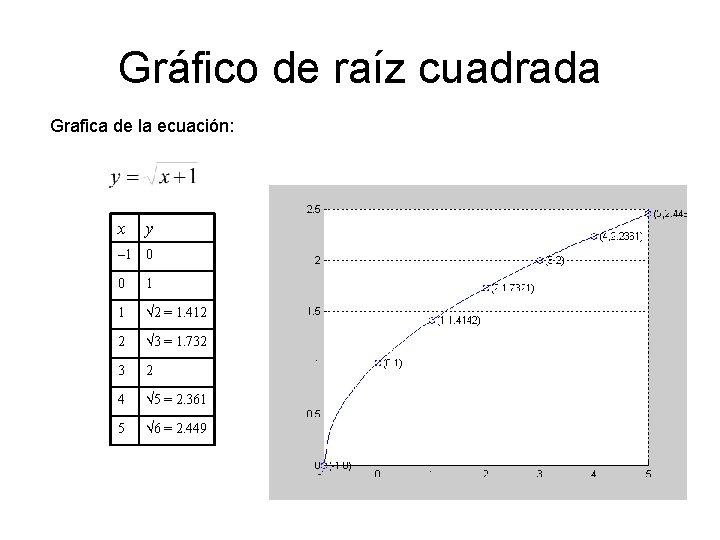
Gráfico de raíz cuadrada Grafica de la ecuación: x y – 1 0 0 1 1 2 = 1. 412 2 3 = 1. 732 3 2 4 5 = 2. 361 5 6 = 2. 449

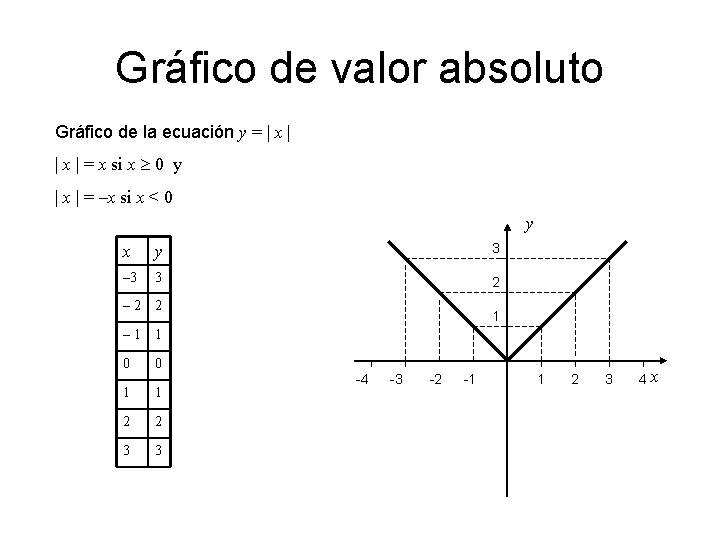
Gráfico de valor absoluto Gráfico de la ecuación y = | x | = x si x 0 y | x | = –x si x < 0 y x y 3 – 3 3 2 – 2 2 – 1 1 0 0 1 1 2 2 3 3 1 -4 -3 -2 -1 1 2 3 4 x

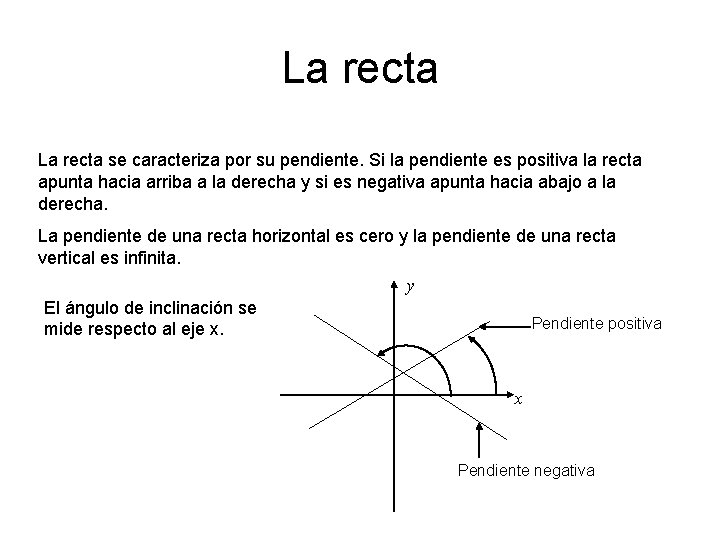
La recta se caracteriza por su pendiente. Si la pendiente es positiva la recta apunta hacia arriba a la derecha y si es negativa apunta hacia abajo a la derecha. La pendiente de una recta horizontal es cero y la pendiente de una recta vertical es infinita. y El ángulo de inclinación se mide respecto al eje x. Pendiente positiva x Pendiente negativa

Definición de pendiente Dados puntos P 1(x 1, y 1) y P 2(x 2, y 2), definimos el avance como Dx = x 2 – x 1 P 2’ y el ascenso como Dy = y 2 – y 1 La pendiente se define como Los triángulos P 1 QP 2 y P 1’Q’P 2’ son semejantes, asi que P 2(x 2, y 2) f Dy ascenso Dy’ P 1(x 1, y 1) Dx P 1’ Q(x 2, y 1) avance Dx’ Q’

Rectas paralelas y perpendiculares Dos rectas L 1 y L 2 con pendientes m 1 y m 2 son paralelas si y solo si tienen la misma pendiente, o sea, m 1 = m 2. Dos rectas L 1 y L 2 con pendientes m 1 y m 2 son perpendiculares si y solo si m 1 = – 1/m 2. Demostración Si L 1 y L 2 son ’s a 2 – a 2 = 90° cos(a 2 – a 1 )= 90° = 0 cos(a 2 – a 1 )= cosa 2 cos a 1+sena 2 sen a 1 = 0 dividiendo entre cosa 2 cos a 1 1 + tana 2 tan a 1 = 1 + m 1 m 2 = 0 a 2 – a 1 a 2 a 1

Tarea #4 1. Calcule el ángulo que hacen con el eje x las siguientes rectas si su pendiente es a) m = 2. 5 b) m = 1. 3 c) m = -0. 5 d ) m = -1. 25 2. Diga si las siguientes rectas definidas por cada par de puntos son paralelas o perpendiculares o ninguna. A(3, 1) y B(-2, 5) C(-4, 2) y D(4, 12) 3. Mostrar por medio de la pendiente que los siguientes puntos son colineales: a) (1, -1), (-2, 5), (3, -5) b) (2, 0), (4, 1), (-6, -4) c) (-1, 1), (2, 3), (-4, -1) d) (-6, 3), (4, -1), (3, -3/5)

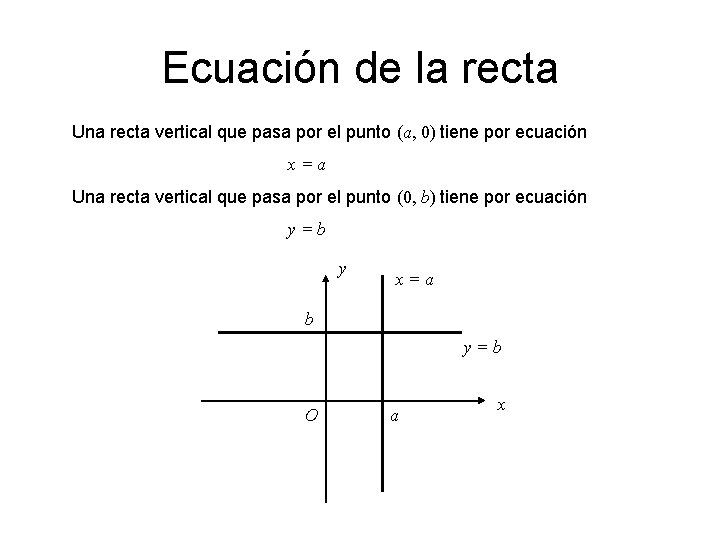
Ecuación de la recta Una recta vertical que pasa por el punto (a, 0) tiene por ecuación x=a Una recta vertical que pasa por el punto (0, b) tiene por ecuación y=b y x=a b y=b O a x

Ecuación dada la pendiente Si conocemos la pendiente de una recta que pasa por el punto P(x 1, y 1), podemos encontrar su ecuación. Sea P(x, y) cualquier punto sobre la recta, entonces y o y – y 1 = m(x – x 1) P(x 1, y 1) m y = y 1 + m(x – x 1) O x

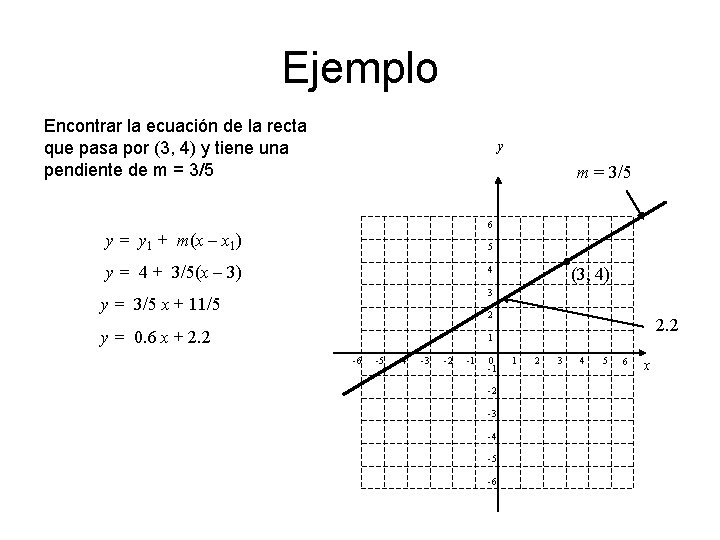
Ejemplo Encontrar la ecuación de la recta que pasa por (3, 4) y tiene una pendiente de m = 3/5 y m = 3/5 6 y = y 1 + m(x – x 1) 5 y = 4 + 3/5(x – 3) (3, 4) 4 3 y = 3/5 x + 11/5 2 y = 0. 6 x + 2. 2 1 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 1 2 3 4 5 6 x

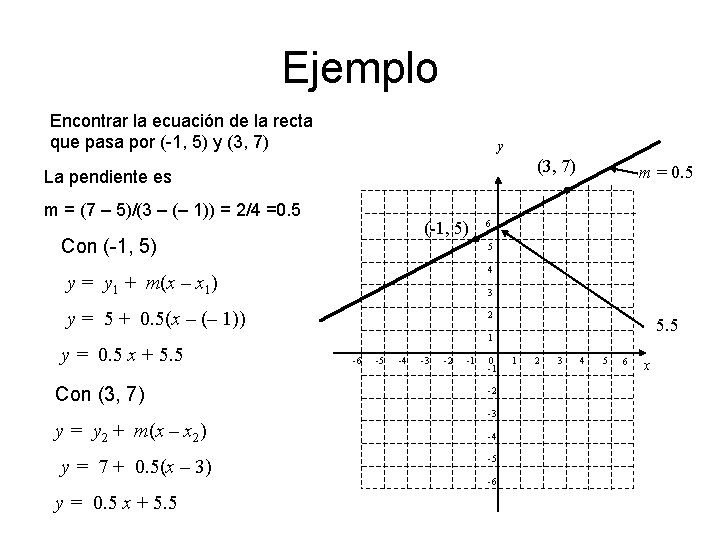
Ejemplo Encontrar la ecuación de la recta que pasa por (-1, 5) y (3, 7) La pendiente es m = (7 – 5)/(3 – (– 1)) = 2/4 =0. 5 (-1, 5) Con (-1, 5) m = 0. 5 6 5 4 y = y 1 + m(x – x 1) 3 y = 5 + 0. 5(x – (– 1)) 2 5. 5 1 y = 0. 5 x + 5. 5 Con (3, 7) y = y 2 + m(x – x 2) y = 7 + 0. 5(x – 3) y = 0. 5 x + 5. 5 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 1 2 3 4 5 6 x

Ordenada al origen La coordenada y donde una recta no vertical corta el eje y se llama “ordenada al origen” , y se designa por b. Sustituyendo en la ecuación de la recta el punto (0, b) se obtiene y = b + m(x – 0) y=mx+b Esta es la ecuación pendiente-ordenada al origen.

Ecuación general de la recta La ecuación general de la recta tiene la forma: Ax + By = C Esta ecuación puede representar cualquier recta Ec. general Valores de A, B, C Forma de pendiente-ordenada – 5 x + 8 y = 6 A= – 5, B = 8, C = 6 y = 0. 625 x + 0. 75 x+y=3 A= 1, B = 1, C = 3 y=–x+3 x = – 2 A= 1, B = 0, C = – 2 no es posible y=5 A= 0, B = 1, C = 5 no es posible

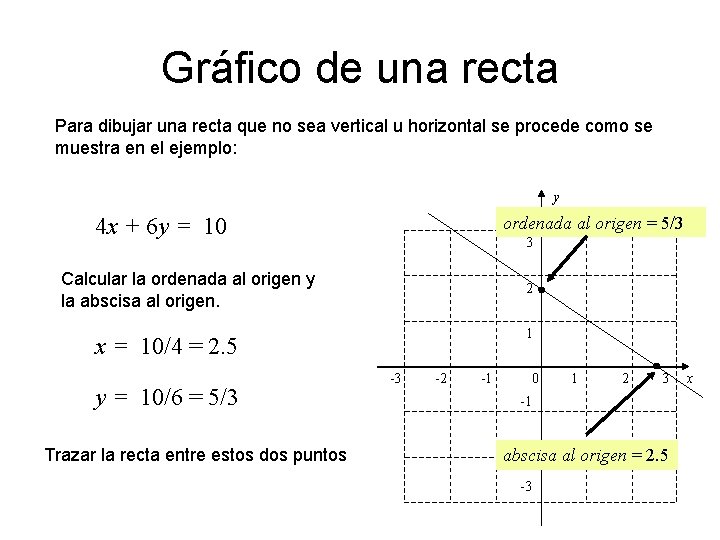
Gráfico de una recta Para dibujar una recta que no sea vertical u horizontal se procede como se muestra en el ejemplo: y ordenada al origen = 5/3 4 x + 6 y = 10 3 Calcular la ordenada al origen y la abscisa al origen. 2 1 x = 10/4 = 2. 5 y = 10/6 = 5/3 Trazar la recta entre estos dos puntos -3 -2 -1 0 1 2 3 -1 -2 abscisa al origen = 2. 5 -3 x

Tarea #5 Encuentre la ecuación de la recta dados a) el punto (2, – 3) y la pendiente m = 1/2 b) la pendiente 1/2 y la ordenada al origen b = – 3 c) pasa por (5, – 1) y es paralela a la recta 2 x + 5 y = 5 d) pasa por (4, 10) y es perpendicular a la recta 6 x – 3 y = 5 Dibuje la recta encontrando primero la ordenada y la abscisa al origen para la recta 1. 5 x – y = – 3

Funciones Una función de un conjunto D a un conjunto I es una regla que asigna un único elemento f(x) de I a cada elemento de D. f D I El conjunto D = D(f) (“D de f”) es el dominio de la función f e I es el conjunto imagen. Las funciones se expresan mediante una fórmula: y = expresión O f(x) = expresión

Ejemplo de funciones El volumen de una esfera depende del radio de esta. V=4 pr 3/3 O V(r) = 4 p r 3 / 3 Ejemplo: V(2) = 4 p 2 3 / 3 = 33. 5 m 3 Área y perímetro de un triángulo equilátero como función de la longitud de un lado x. Área = A = base x altura /2 = perímetro = P = 3 x

Dominio e imagen El dominio de una función puede ser el conjunto de los números reales o puede estar restringido Función Dominio Imagen y = x 2 (– , ) [0, ) [– 1, 1] [0, 1] y = 1/x (– , 0) (0, ) y = x 2/(x – 1) (– , 1) (1, ) (– , )

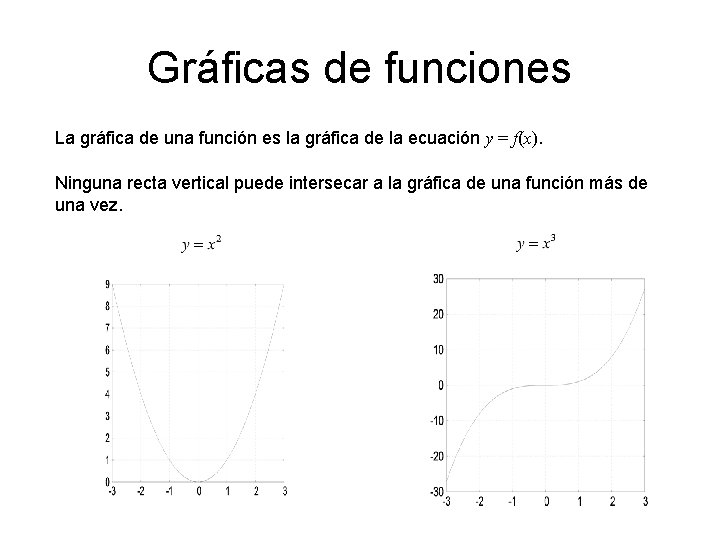
Gráficas de funciones La gráfica de una función es la gráfica de la ecuación y = f(x). Ninguna recta vertical puede intersecar a la gráfica de una función más de una vez.

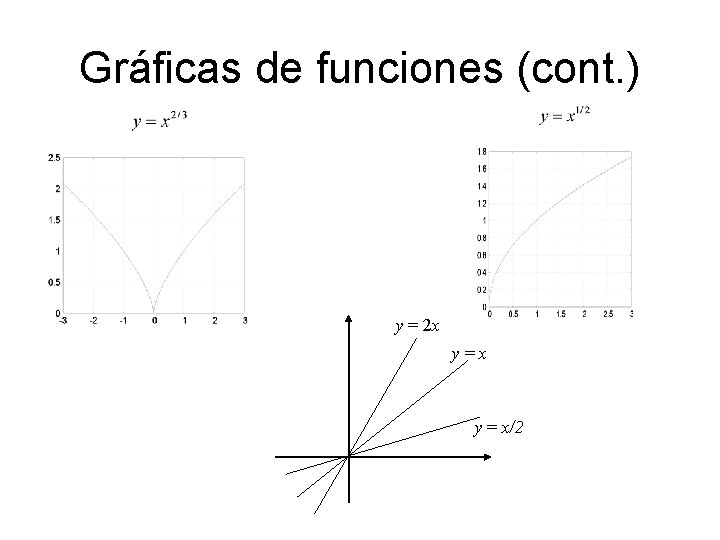
Gráficas de funciones (cont. ) y = 2 x y=x y = x/2

Operaciones con funciones Operaciones aritméticas Suma: (f + g)(x) = f (x) + g(x) Resta: (f - g)(x) = f (x) - g(x) Multiplicación: (f g)(x) = f (x) g(x) División: (f / g)(x) = f (x) / g(x) Multiplicación: (c f)(x) = c f (x) por constante

Ejemplo de operaciones Función fórmula dominio f f(x) = x 2 (– , ) g g(x) = 1 + x [-1, ) 3 f 3 f(x) = 3 x 2 (– , ) f–g (f – g)(x) = x 2 – 1 + x [-1, ) f g (fg)(x) = x 2 1 + x [-1, ) f /g (f / g)(x) = x 2 / 1 + x (-1, ) g /f (g / f)(x) = 1 + x / x 2 [-1, 0) (0, )

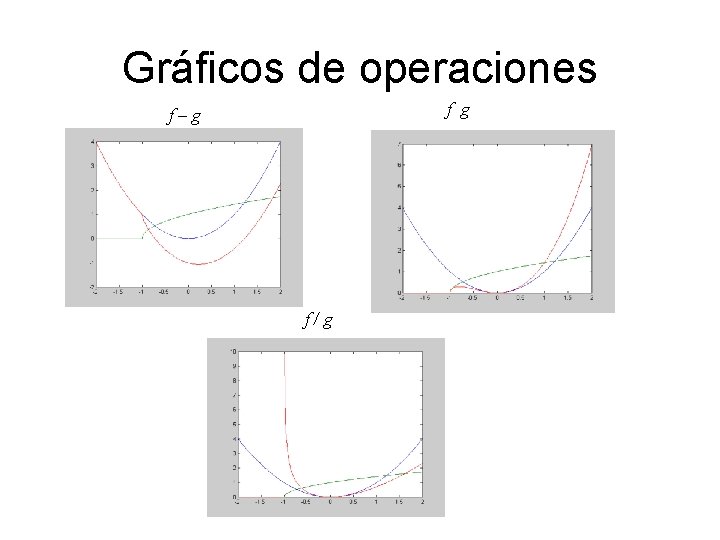
Gráficos de operaciones f g f–g f/g

Composición de funciones Definición Si f y g son funciones, la composición f ° g (“f círculo g”) es la función definida mediante (f ° g) (x) = f(g(x)) El dominio de f ° g consiste de todos los números y del dominio de g para los cuales g(x) está en el dominio de f. f°g f (g(x)) g f

Ejemplos de composición

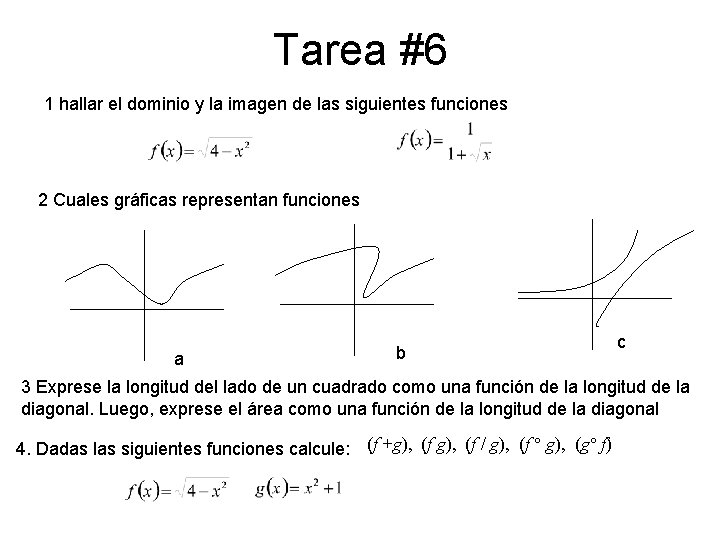
Tarea #6 1 hallar el dominio y la imagen de las siguientes funciones 2 Cuales gráficas representan funciones a b c 3 Exprese la longitud del lado de un cuadrado como una función de la longitud de la diagonal. Luego, exprese el área como una función de la longitud de la diagonal 4. Dadas las siguientes funciones calcule: (f +g), (f / g), (f ° g), (g° f)

Funciones pares e impares una función y = f(x) es par si f(-x) = f(x) para toda x del dominio de f. una función y = f(x) es impar si f(-x) = -f(x) para toda x del dominio de f. Funciones pares Funciones impares

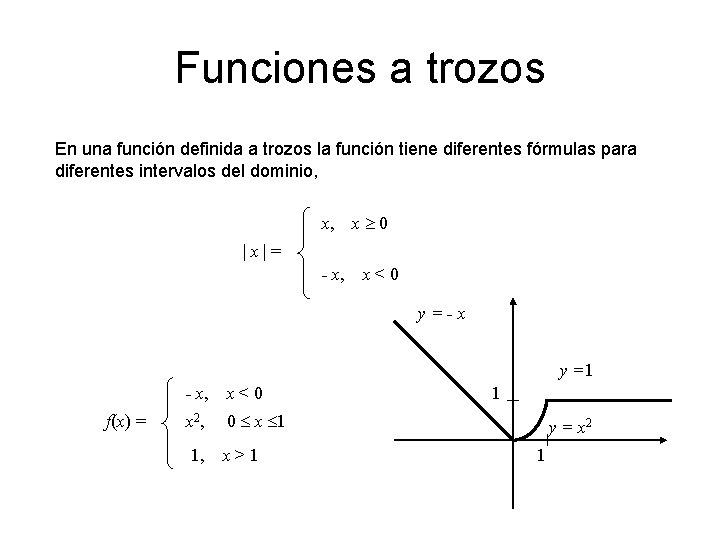
Funciones a trozos En una función definida a trozos la función tiene diferentes fórmulas para diferentes intervalos del dominio, x, x 0 |x|= - x, x < 0 y=-x y =1 - x, x < 0 f(x) = x 2 , 1 0 x 1 1, x > 1 y = x 2 1

Función máximo entero Se define como el mayor entero menor o igual que x o función piso entero (floor). Se denota por: 3 y=x 2 1 1 -1 2 3

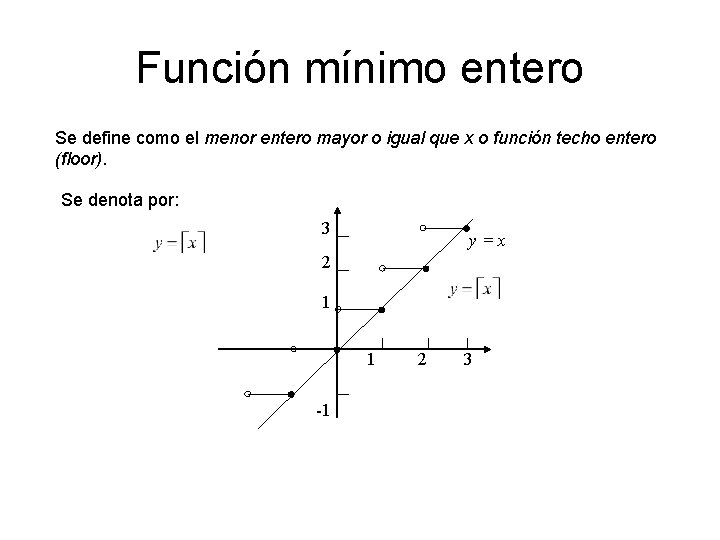
Función mínimo entero Se define como el menor entero mayor o igual que x o función techo entero (floor). Se denota por: 3 y=x 2 1 1 -1 2 3

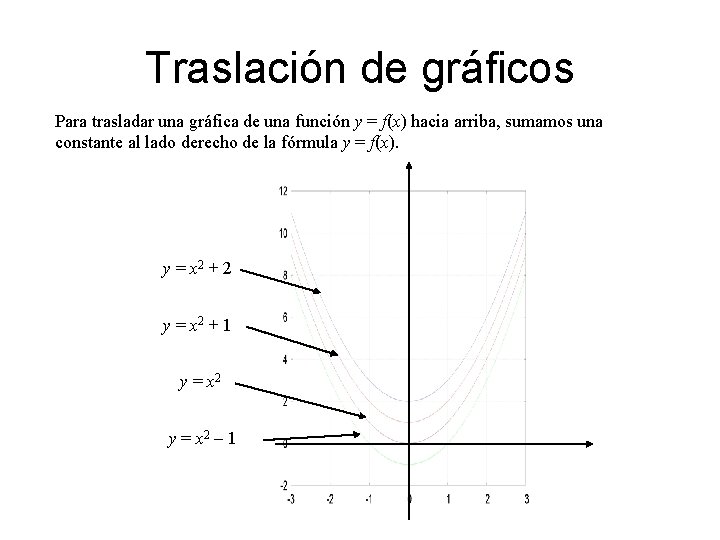
Traslación de gráficos Para trasladar una gráfica de una función y = f(x) hacia arriba, sumamos una constante al lado derecho de la fórmula y = f(x). y = x 2 + 2 y = x 2 + 1 y = x 2 – 1

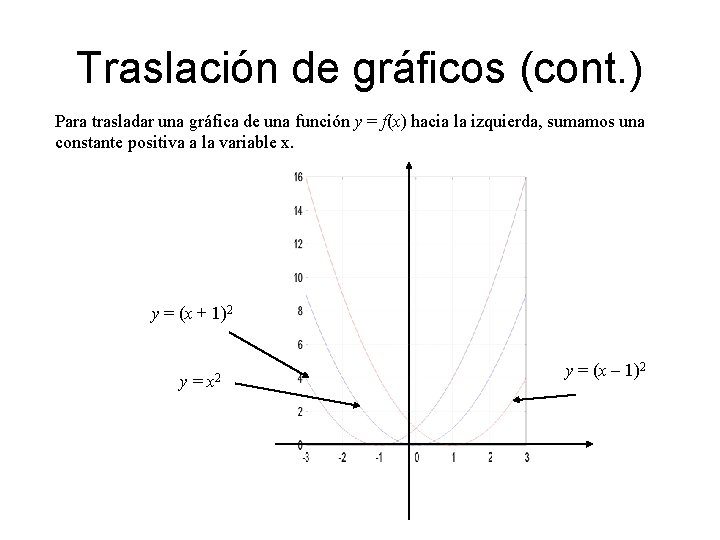
Traslación de gráficos (cont. ) Para trasladar una gráfica de una función y = f(x) hacia la izquierda, sumamos una constante positiva a la variable x. y = (x + 1)2 y= x 2 y = (x – 1)2

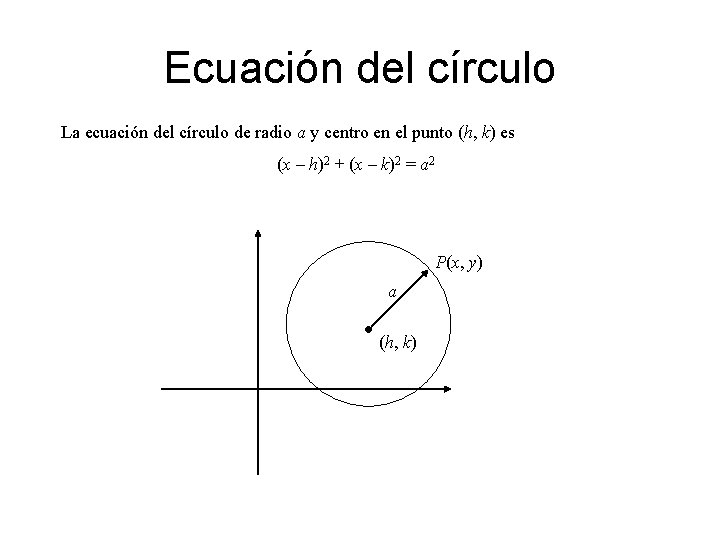
Ecuación del círculo La ecuación del círculo de radio a y centro en el punto (h, k) es (x – h)2 + (x – k)2 = a 2 P(x, y) a (h, k)

Ejemplo La ecuación del circulo con centro en (4, 6) y radio 3. 5 es (x – 4)2 + (y – 6)2 = 3. 52 = 12. 25 Encontrar el centro y el radio del círculo x 2 + y 2 + 4 x – 6 y – 3 = 0 Agrupando los términos con x y con y y completando el cuadrado x 2 + 4 x + y 2 – 6 y – 3 = 0 x 2 + 4 x + 4 + y 2 – 6 y + 9 – 4 – 9 – 3 = 0 (x + 2)2 + (y 2 – 3)2 = 16 Centro en (– 2, 3) y radio = 4

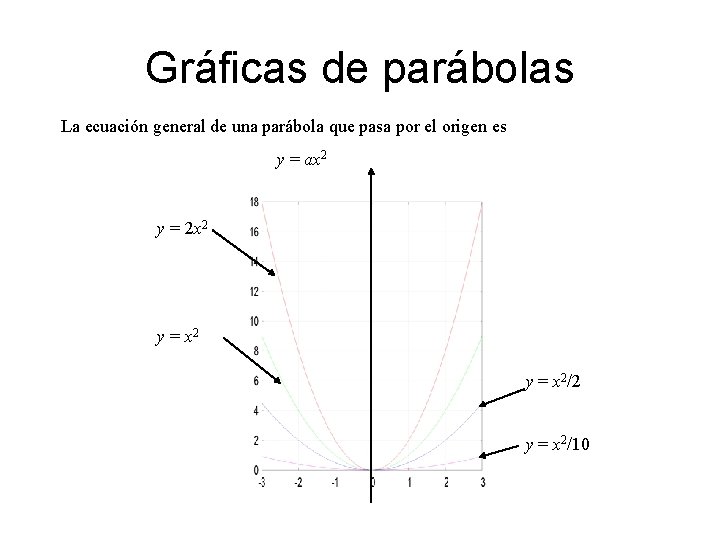
Gráficas de parábolas La ecuación general de una parábola que pasa por el origen es y = ax 2 y = 2 x 2 y = x 2/2 y = x 2/10

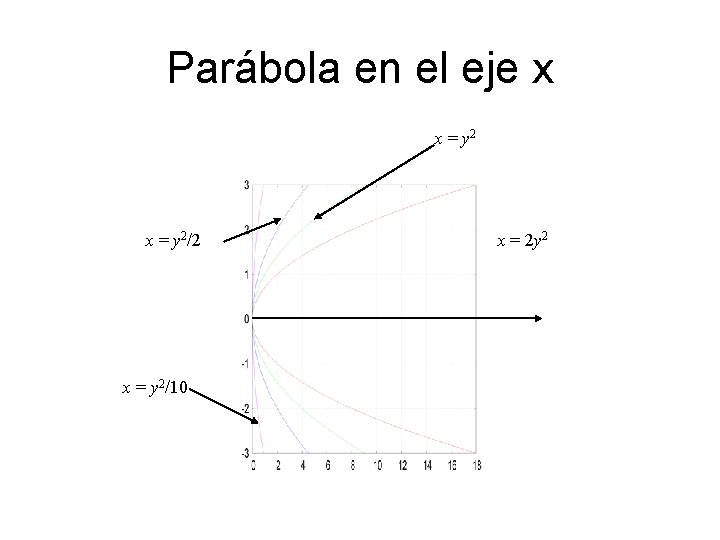
Parábola en el eje x x = y 2/2 x = y 2/10 x = 2 y 2

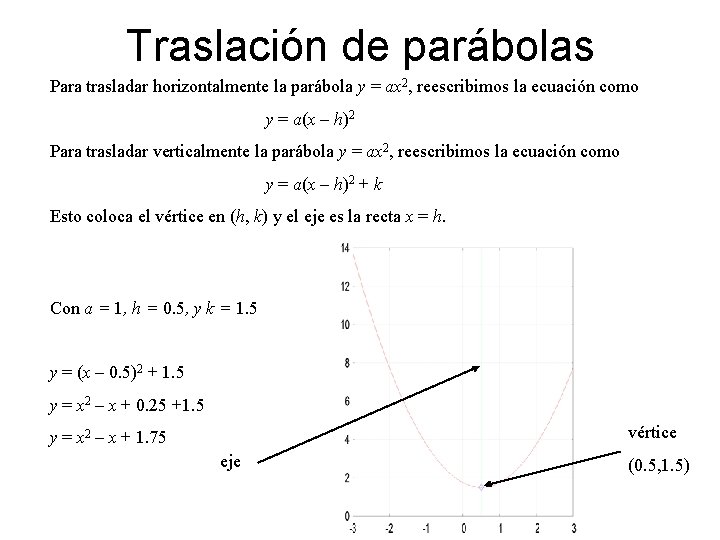
Traslación de parábolas Para trasladar horizontalmente la parábola y = ax 2, reescribimos la ecuación como y = a(x – h)2 Para trasladar verticalmente la parábola y = ax 2, reescribimos la ecuación como y = a(x – h)2 + k Esto coloca el vértice en (h, k) y el eje es la recta x = h. Con a = 1, h = 0. 5, y k = 1. 5 y = (x – 0. 5)2 + 1. 5 y = x 2 – x + 0. 25 +1. 5 vértice y = x 2 – x + 1. 75 eje (0. 5, 1. 5)

Parábola general La gráfica de y = ax 2 + bx + c, a 0, es una parábola. Se abre hacia arriba si a > 0, y hacia abajo si a < 0. el eje es la recta x = –b/2 a El vértice de la parábola es el punto donde la parábola y su eje se intersecan. Su coordenada x es –b/2 a, su coordenada y se encuentra sustituyendo x = – b/2 a en la ecuación de la parábola.

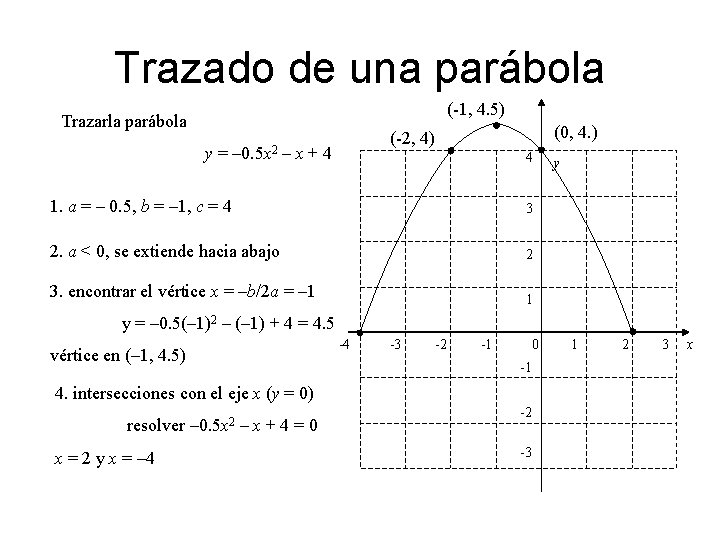
Trazado de una parábola (-1, 4. 5) Trazarla parábola (0, 4. ) (-2, 4) y = – 0. 5 x 2 – x + 4 4 1. a = – 0. 5, b = – 1, c = 4 3 2. a < 0, se extiende hacia abajo 2 3. encontrar el vértice x = –b/2 a = – 1 1 y y = – 0. 5(– 1)2 – (– 1) + 4 = 4. 5 vértice en (– 1, 4. 5) -4 -3 -2 -1 0 -1 4. intersecciones con el eje x (y = 0) resolver – 0. 5 x 2 – x + 4 = 0 x = 2 y x = – 4 -2 -3 1 2 3 x

Funciones Trigonométricas Medición en radianes La medida en radianes q de un ángulo ABC se define como la longitud del arco circular AB en un círculo de radio unitario. Para cualquier otro círculo un radian es la razón de la longitud del arco al radio del círculo. B q q 1 A C Un ángulo de 360 tiene 2 p radianes, un radian serán 360/2 p = 57. 3°

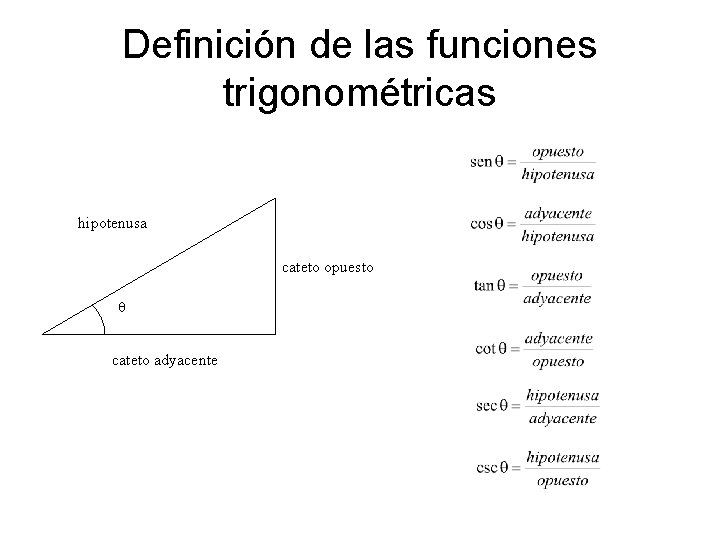
Definición de las funciones trigonométricas hipotenusa cateto opuesto q cateto adyacente

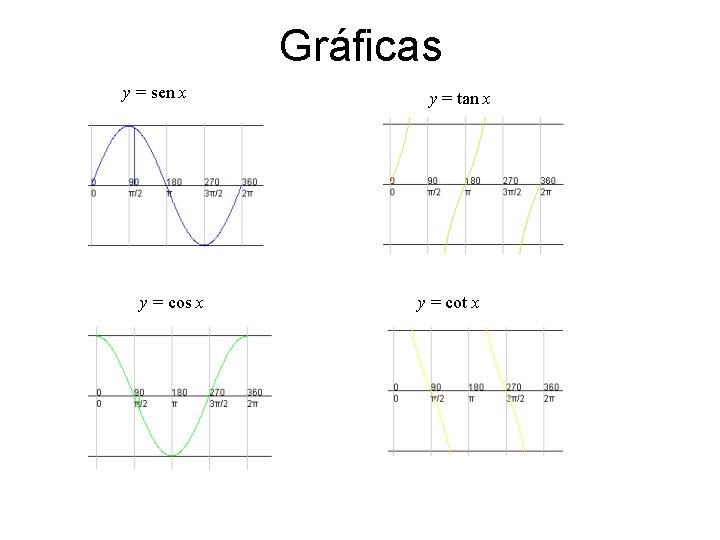
Gráficas y = sen x y = cos x y = tan x y = cot x

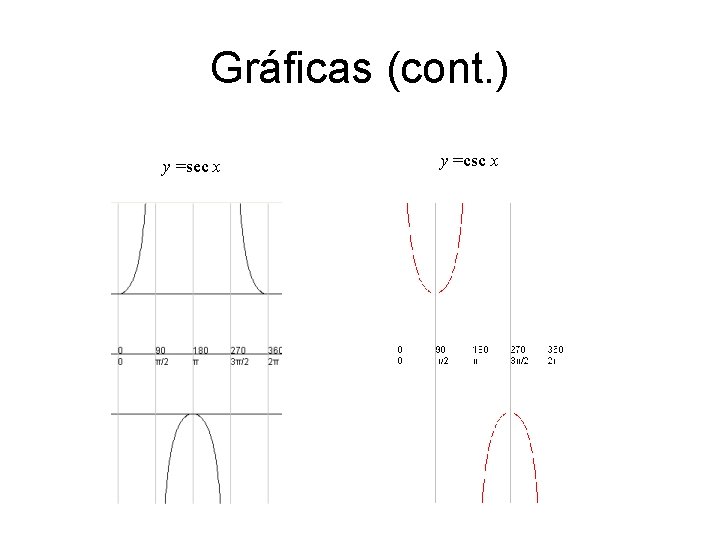
Gráficas (cont. ) y =sec x y =csc x

Periodicidad Una función es periódica si existe un número positivo p tal que f(x + p) = f(x). El valor mínimo posible de p es el periodo de f(x). Periodo p: tan(x + p) = tan(x) cot(x + p) = cot(x) Periodo 2 p: sen(x + 2 p) = sen(x) cos(x + 2 p) = cos(x) sec(x + 2 p) = sec(x) csc(x + 2 p) = csc(x)

Funciones trig. pares e impares Pares: cos(–x) = cos(x) sec(–x) = sec(x) Impares: sen(–x) = –sen(x) tan(–x) = –tan(x) cot(–x) = –cot(x) csc(–x) = –csc(x)

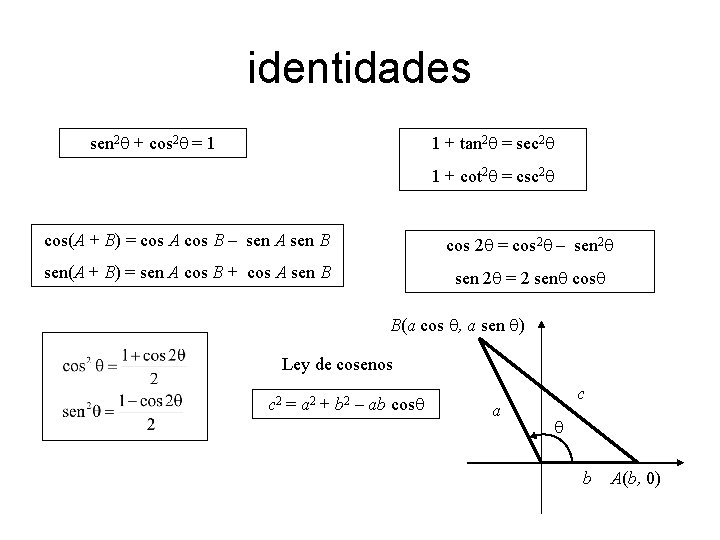
identidades sen 2 q + cos 2 q = 1 1 + tan 2 q = sec 2 q 1 + cot 2 q = csc 2 q cos(A + B) = cos A cos B – sen A sen B cos 2 q = cos 2 q – sen 2 q sen(A + B) = sen A cos B + cos A sen B sen 2 q = 2 senq cosq B(a cos q, a sen q) Ley de cosenos c 2 = a 2 + b 2 – ab cosq a c q b A(b, 0)

Tarea #8 En un círculo de radio 10, ¿que longitud tiene el arco que subtiende un ángulo central de a) 4 p/5 radianes b) 110°? Se da el valor del sen x, cos x o tan x. Encuentra los dos restantes sen x =3/5 x en [p /2, p] cos x = 1/3 x en [ - p /2, 0] tan x = 1/2 x en [p , 3 p/2]

-6 -5 -4 -3 -2 -1 -6 -5 -4 -3 -2 0 -1 1 2 3 4 5 6 1 y 2 1. 5 x – y = – 3 3 4 5 6 Dibuje la recta encontrando primero la ordenada y la abscisa al origen para la recta d) pasa por (4, 10) y es perpendicular a la recta 6 x – 3 y = 5 c) pasa por (5, – 1) y es paralela a la recta 2 x + 5 y = 5 b) la pendiente 1/2 y la ordenada al origen b = – 3 a) el punto (2, – 3) y la pendiente m = 1/2 Encuentre la ecuación de la recta dados Tarea #5 x

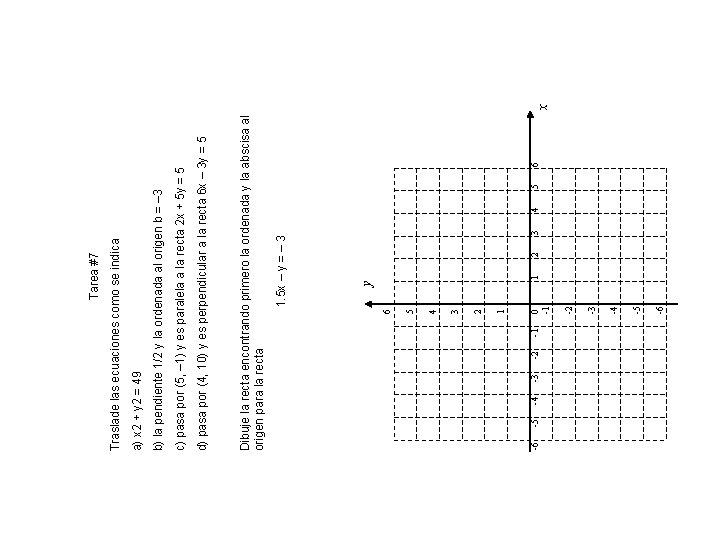
-6 -5 -4 -3 -2 -1 -6 -5 -4 -3 -2 0 -1 1 2 3 4 5 6 1 y 2 1. 5 x – y = – 3 3 4 5 6 Dibuje la recta encontrando primero la ordenada y la abscisa al origen para la recta d) pasa por (4, 10) y es perpendicular a la recta 6 x – 3 y = 5 c) pasa por (5, – 1) y es paralela a la recta 2 x + 5 y = 5 b) la pendiente 1/2 y la ordenada al origen b = – 3 a) x 2 + y 2 = 49 Traslade las ecuaciones como se indica Tarea #7 x

y 6 5 4 3 2 1 -6 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 -6 11 2 3 4 5 6 x