Funciones 1 parte Asignatura Lmite Derivada e Integrales

Funciones 1º parte Asignatura: Límite, Derivada e Integrales. Curso: III º Medio. Profesora: Alejandra Cañete Valenzuela.

Introducción histórica Descartes y Fermat estudiaron en profundidad las curvas y sus ecuaciones, pero las habían tratado como casos individualizados. A partir de ellos, muchos matemáticos a lo largo del siglo XVII se esforzaron en el estudio de las curvas, pero ninguno dio con los elementos que permitían establecer un método general. Newton y Leibniz lo proporcionaron, e introdujeron un tipo de técnicas que permitían estudiar con las mismas herramientas los problemas de física y geometría. Sus avances en el cálculo diferencial e integral posibilitaron un desarrollo de las matemáticas espectacular, cuyo resultado se apreció posteriormente durante los siglos XVIII y XIX. Desde el punto de vista del desarrollo de la matemática, les corresponde a estos dos autores la elaboración de un método general y nuevo, que puede aplicarse a muchos tipos de problemas sobre el cálculo algebraico, el infinitesimal y, en general, a toda la geometría analítica. El concepto de función se hizo el eje central de la matemática, sobre todo en el análisis. Su estudio se hizo totalmente indispensable para llevar adelante el desarrollo científico y tecnológico. El nombre de “función” proviene del gran matemático Leibniz, y su estudio más profundo sobre funciones fue estimulado por su interés geométrico de analizar, matemáticamente, los puntos de las curvas donde éstas alcanzan su máximo y su mínimo valor y dar un método general para determinar las rectas tangentes es estos puntos. Estos cálculos se realizan mediante el cálculo de las funciones derivadas y forman parte importante del cálculo diferencial, que se estudia más adelante.

Introducción histórica Newton y Leibniz, los dos grandes científicos de finales del siglo XVII y principios del XVIII, vivieron en una Europa caracterizada por la revolución del realismo científico y la explosión cultural del Barroco. Newton, en su obra ”Methodus fluxionum et serierum infiniturum”, introduce su nueva concepción de fluxiones y fluentes al abordar dos problemas; el primero consiste en encontrar la velocidad del movimiento en un tiempo dado cualquiera, dada la longitud del espacio descrito. El segundo problema es la inversa del primero. Disponiendo de su método general, determina los máximos y mínimos de relaciones, las tangentes a curvas, el radio de curvatura, los puntos de inflexión y el cambio de concavidad de las curvas, su área y su longitud. Isaac Newton (1642 -1727) Gottfried Leibniz (1646 -1716)

Justificación ¢ Las funciones nacen de la necesidad de resolver problemas prácticos y se sustentan por su capacidad para tratar, explicar, predecir y modelar situaciones reales y dar rigor a los conocimientos científicos. ¢ Tienen una fuerte conexión con la realidad, debido a su constante interrelación con otras áreas, especialmente en el ámbito de la ciencia y la técnica. ¢ El estudio de las funciones es principalmente estratégico y se manifiesta en tres aspectos: como base conceptual, como instrumento esencial de desarrollo de la Ciencia y la Tecnología y como valor inherente a la propia cultura. ¢ Los estudiantes deben aprender a apreciar la utilidad de las funciones, sobre todo, su capacidad para dar respuesta a la mayoría de las necesidades humanas.

Objetivos ¢ Calcular dominios y recorridos de funciones reales de variable real. ¢ Distinguir correspondencias funcionales de las que no lo son. ¢ Identificar funciones creciente/decreciente, monótona en un intervalo y saber aplicar esos conceptos al análisis de funciones elementales. Representar gráficamente funciones polinómicas, racionales, radicales, exponenciales, logarítmicas, trigonométricas y algunas transformaciones de dichas funciones ¢ ¢ Conocer y aplicar los conceptos de función par/impar, así como las simetrías correspondientes de sus gráficas. ¢ Saber qué son funciones periódicas y distinguir su periodo gráficamente.

Contenidos ¢ Conceptuales: l l l l Concepto de función. Dominio e imagen de una función. Gráficas de funciones polinómicas, racionales, radicales, exponenciales, logarítmicas, trigonométricas Simetrías. Crecimiento y decrecimiento. Máximos y mínimos. Funciones periódicas. Asíntotas.

¿Qué está en función de? ¢ Haga corresponder las columnas El precio del transporte La velocidad El camino recorrido La altura La presión atmosférica El precio del petróleo

¿Qué significan? A cada precio del petróleo le corresponde un precio de transporte A cada velocidad le corresponde un camino recorrido A cada altura le corresponde una presión atmosférica

Variable: es algo que cambia, hay variables que son independientes y otras dependientes. Independientes Dependientes Precio del petróleo Precio del transporte altura Presión atmosférica velocidad Distancia recorrida

Función: ¢ ¢ Una función , es un tipo de relación (correspondencia) que existe entre dos variables f: A B en donde a cada elemento perteneciente al conjunto de partida A (variable independiente), le corresponde un único elemento del conjunto de llegada B (variable dependiente). Se puede representar en un Diagrama. A f B x Y=f(x)

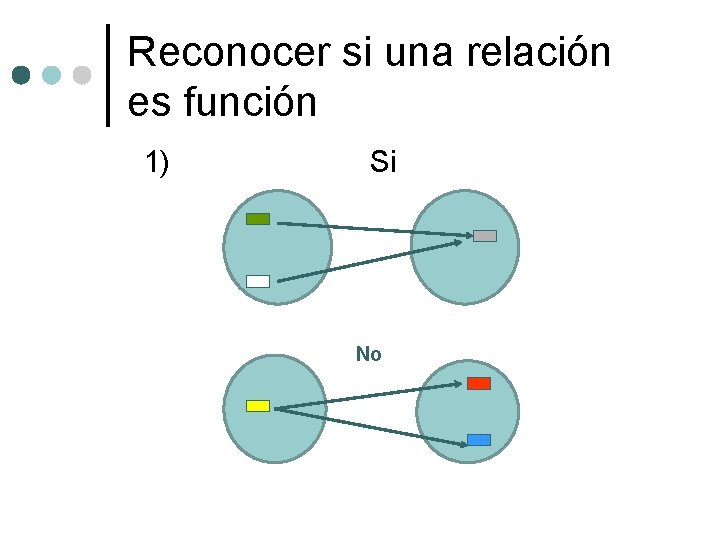
Reconocer si una relación es función 1) Si No

2)

Relaciones no funcionales Ejemplo 1: El peso de una persona, ¿es función de su altura? Se ha consultado mediante una encuesta a personas y se obtuvo este gráfico. La relación, ¿es función? No es una relación funcional, dada la altura de una persona no se puede determinar su peso exactamente. Hay una relación estadística ya que dada una altura determinada se puede esperar que el peso esté en un cierto intervalo. Ejemplo 2 La siguiente

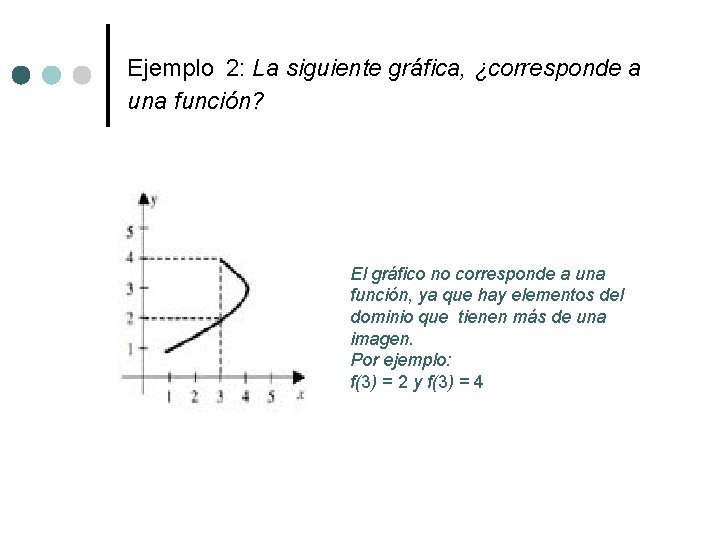
Ejemplo 2: La siguiente gráfica, ¿corresponde a una función? El gráfico no corresponde a una función, ya que hay elementos del dominio que tienen más de una imagen. Por ejemplo: f(3) = 2 y f(3) = 4

Ejemplo 3: La siguiente gráfica, ¿corresponde a una función? Como no se define el dominio de la relación, analicemos dos posibilidades: a) Si el f = [1; 5], entonces el elemento 3 no tiene imagen y no cumple con una condición para ser función, por lo que la relación con ese dominio NO es función. b) Si el Domf f = [1; 5] - {3}, el elemento 3 no forma parte del dominio, por lo tanto, con el dominio así definido, la relación SI es función.

Dominio y Recorrido ¢ Dominio: Conjunto de valores que pueden asignarse a la variable independiente(x), para los cuales la función existe o está definida. (Se denota Domf) ¢ Recorrido o Rango: Conjunto de valores que puede tomar la variable dependiente(y) en una función. (Se denota Recf)

Identificar el dominio y recorrido en un gráfico 1) El dominio es un intervalo del eje x El recorrido es un intervalo del eje y

2) Dom f=[-10, 10] Rec f =[0, 4]

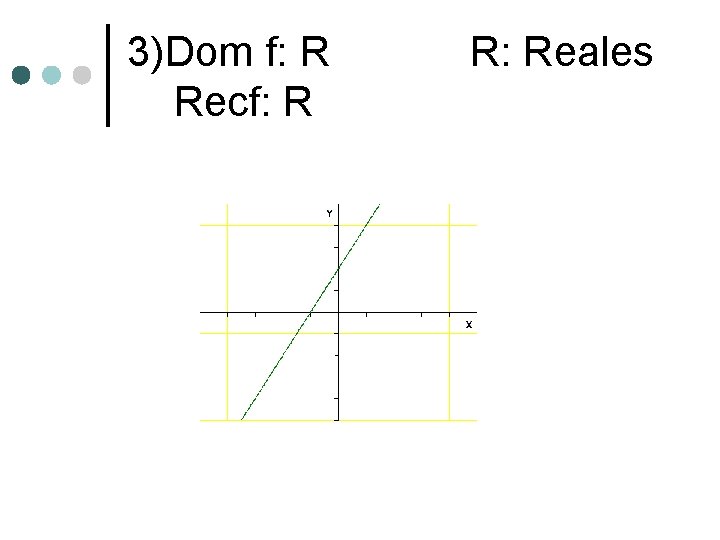
3)Dom f: R Recf: R R: Reales

Funciones definidas por tramos. ¢ ¢ Hay un tipo de funciones que vienen definida con distintas expresiones algebraicas según los valores de x, se dice que están definidas en tramos. Para describir analíticamente una función que está formada por tramos de otras funciones, se dan las expresiones de los distintos tramos, por orden de izquierda a derecha indicando en cada tramo, los valores de x para los que la función está definida.

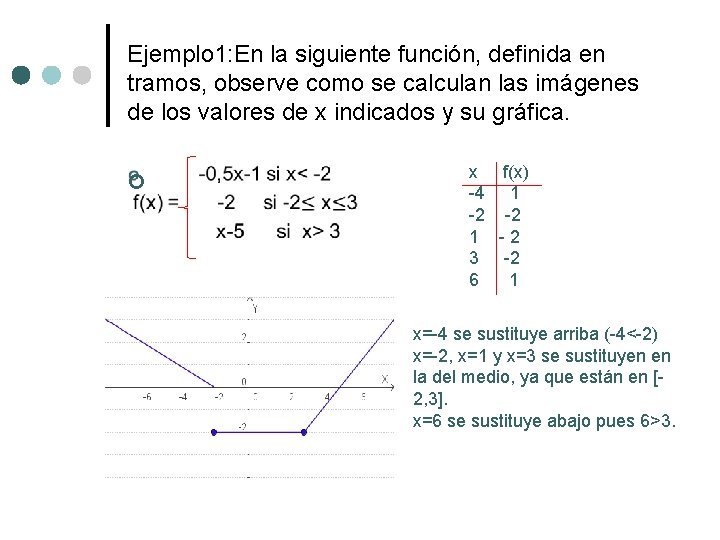
Ejemplo 1: En la siguiente función, definida en tramos, observe como se calculan las imágenes de los valores de x indicados y su gráfica. ¢ x f(x) -4 1 -2 -2 1 -2 3 -2 6 1 x=-4 se sustituye arriba (-4<-2) x=-2, x=1 y x=3 se sustituyen en la del medio, ya que están en [2, 3]. x=6 se sustituye abajo pues 6>3.

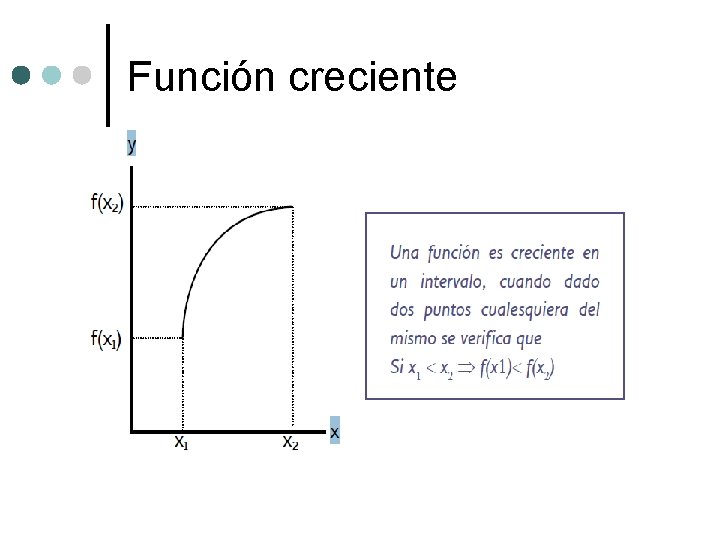
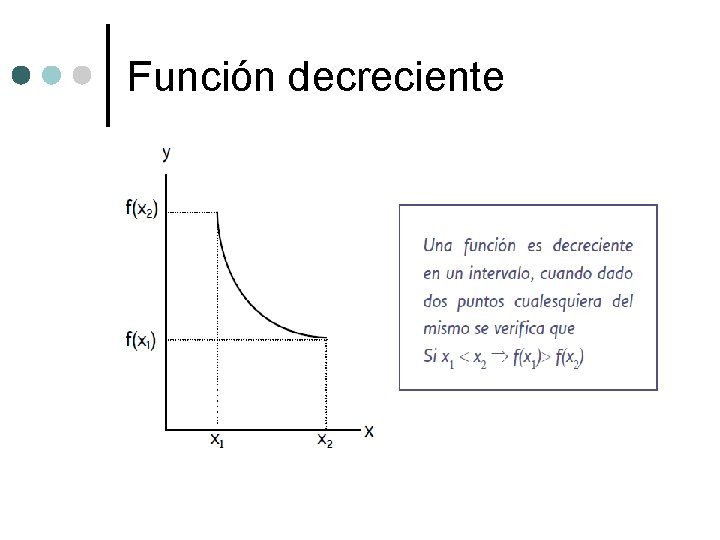
Características del comportamiento de las funciones. ¢ ¢ ¢ Crecimiento y decrecimiento El crecimiento de una función se puede visualizar rápidamente con una inspección en el gráfico, pero se comprueba además, analíticamente que, a medida que la variable independiente aumenta, la variable dependiente también aumenta. El decrecimiento de una función se puede visualizar rápidamente con una inspección en el gráfico, pero se comprueba además, analíticamente que, a medida que la variable independiente aumenta, la variable dependiente disminuye.

Función creciente

Función decreciente

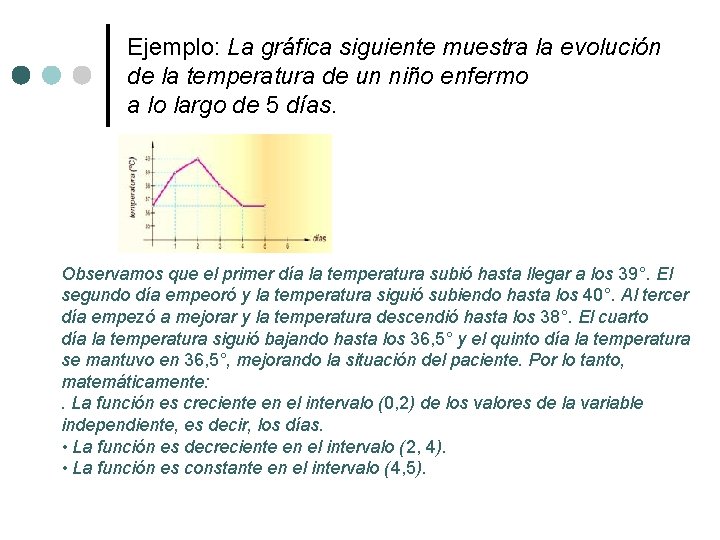
Ejemplo: La gráfica siguiente muestra la evolución de la temperatura de un niño enfermo a lo largo de 5 días. Observamos que el primer día la temperatura subió hasta llegar a los 39°. El segundo día empeoró y la temperatura siguió subiendo hasta los 40°. Al tercer día empezó a mejorar y la temperatura descendió hasta los 38°. El cuarto día la temperatura siguió bajando hasta los 36, 5° y el quinto día la temperatura se mantuvo en 36, 5°, mejorando la situación del paciente. Por lo tanto, matemáticamente: . La función es creciente en el intervalo (0, 2) de los valores de la variable independiente, es decir, los días. • La función es decreciente en el intervalo (2, 4). • La función es constante en el intervalo (4, 5).

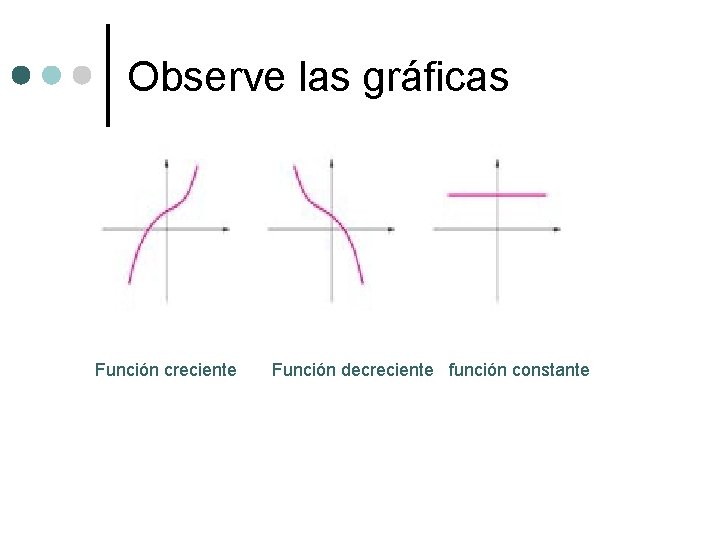
Observe las gráficas Función creciente Función decreciente función constante

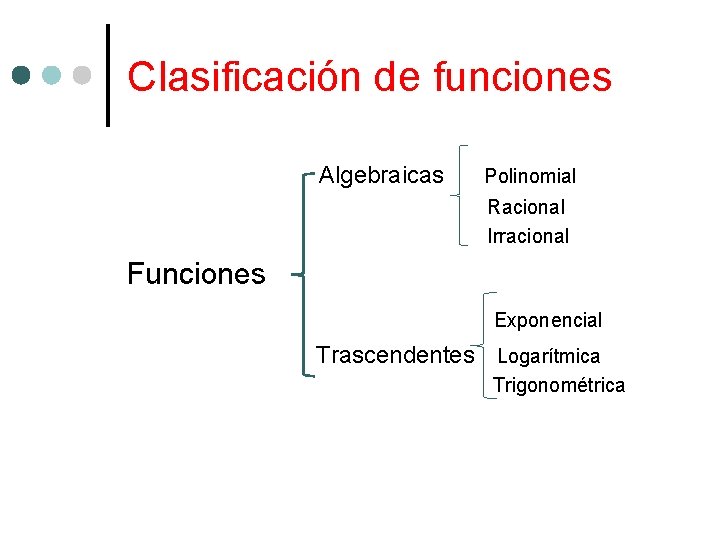
Clasificación de funciones Algebraicas Polinomial Racional Irracional Funciones Exponencial Trascendentes Logarítmica Trigonométrica