Fun with Capacitors Part II Two capacitors are

Fun with Capacitors - Part II

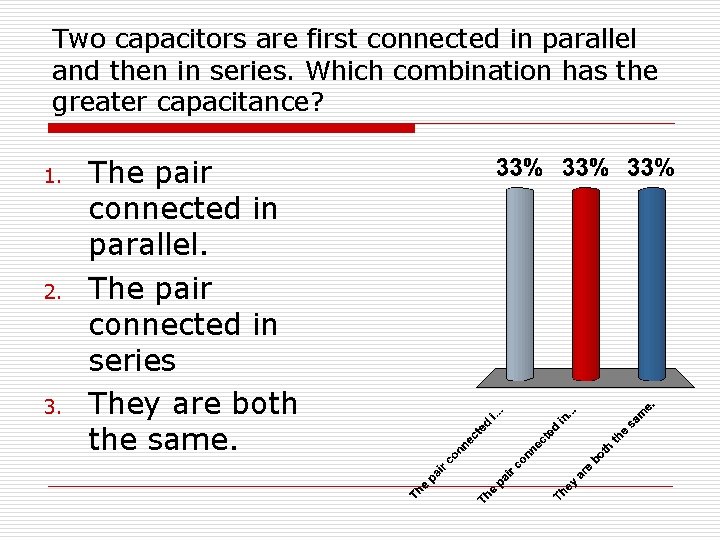
Two capacitors are first connected in parallel and then in series. Which combination has the greater capacitance? 1. 2. 3. The pair connected in parallel. The pair connected in series They are both the same.

Capacitor Circuits

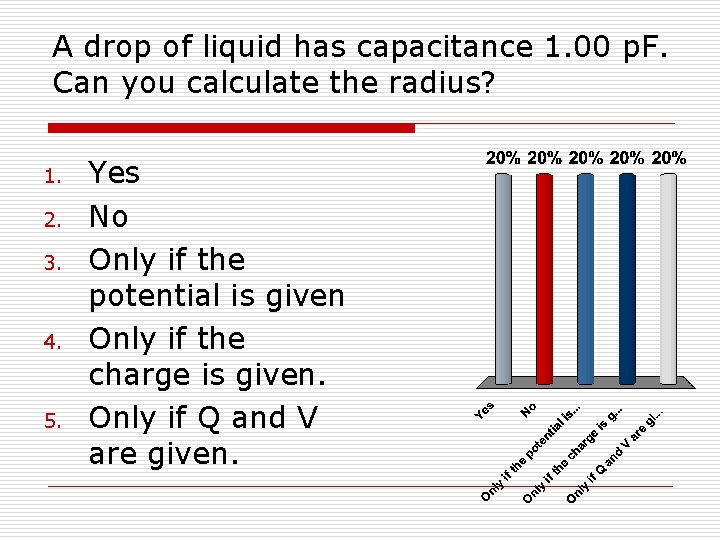
A drop of liquid has capacitance 1. 00 p. F. Can you calculate the radius? 1. 2. 3. 4. 5. Yes No Only if the potential is given Only if the charge is given. Only if Q and V are given.

A Thunker If a drop of liquid has capacitance 1. 00 p. F, what is its radius? STEPS Assume a charge on the drop. Calculate the potential See what happens

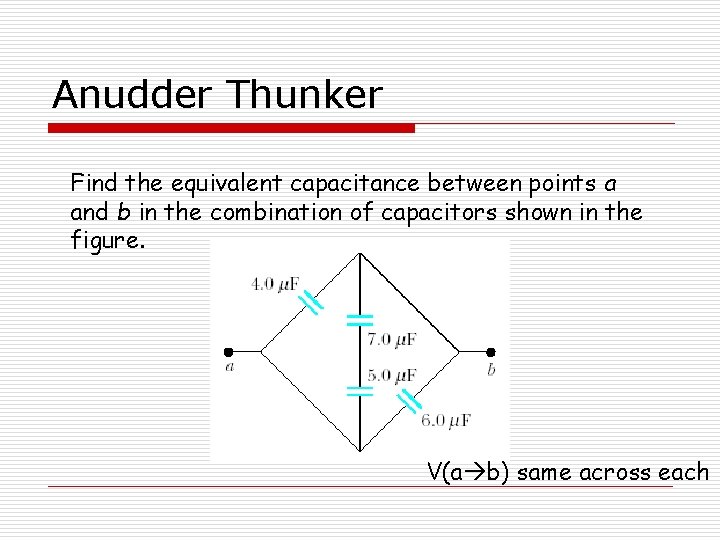
Anudder Thunker Find the equivalent capacitance between points a and b in the combination of capacitors shown in the figure. V(a b) same across each

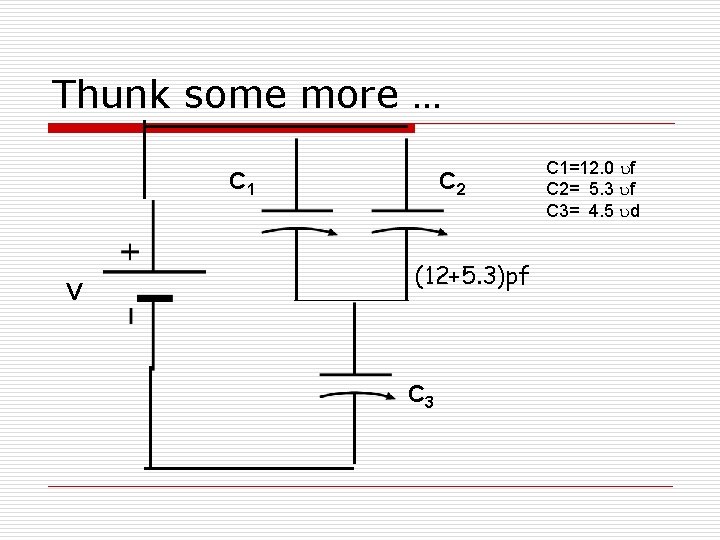
Thunk some more … C 1 V C 2 (12+5. 3)pf C 3 C 1=12. 0 uf C 2= 5. 3 uf C 3= 4. 5 ud

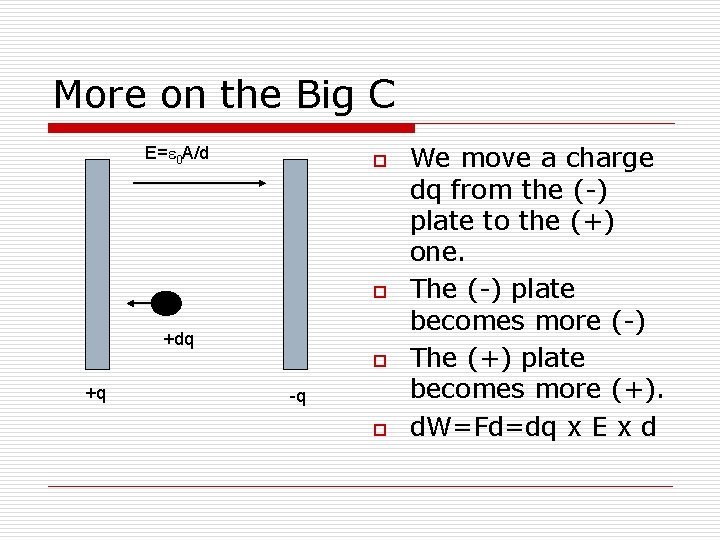
More on the Big C E=e 0 A/d o o +dq o +q -q o We move a charge dq from the (-) plate to the (+) one. The (-) plate becomes more (-) The (+) plate becomes more (+). d. W=Fd=dq x E x d

So…. Sorta like (1/2)mv 2

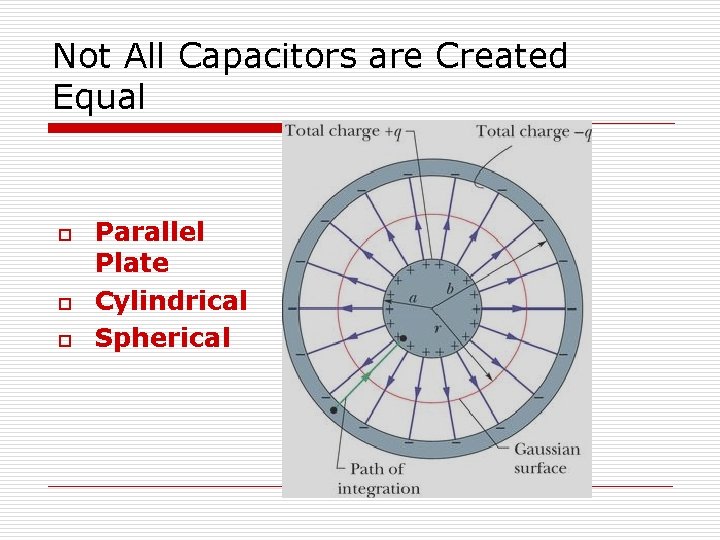
Not All Capacitors are Created Equal o o o Parallel Plate Cylindrical Spherical

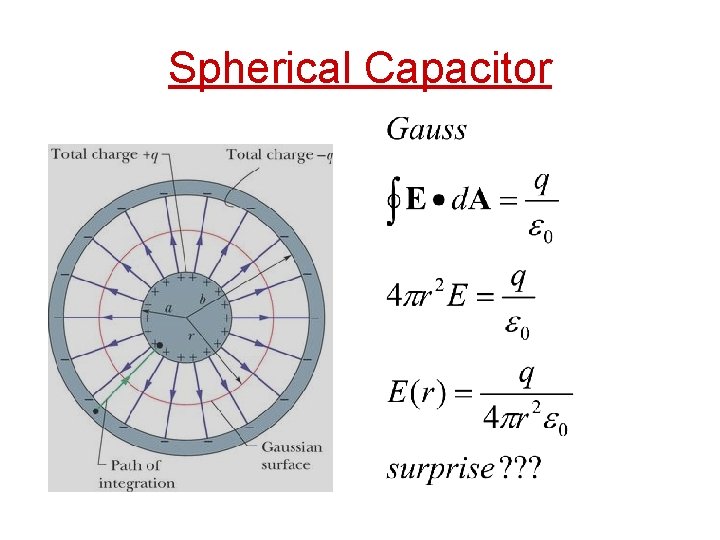
Spherical Capacitor

Calculate Potential Difference V (-) sign because E and ds are in OPPOSITE directions.

Continuing… Lost (-) sign due to switch of limits.

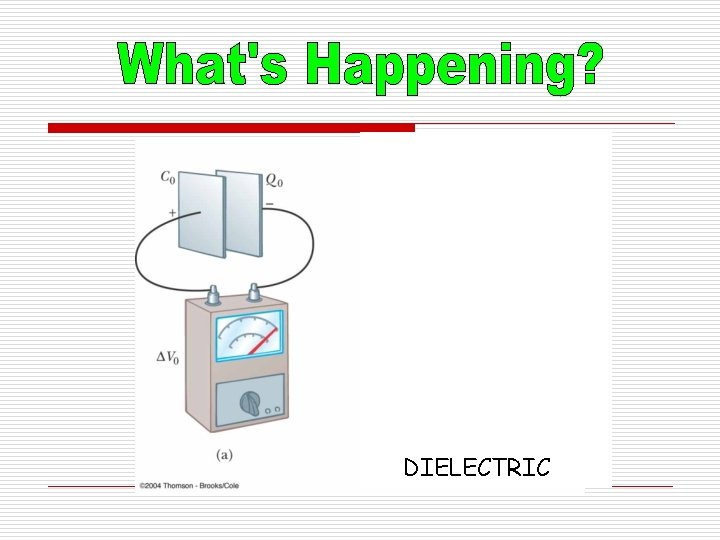
DIELECTRIC

Polar Materials (Water)

If you fill a capacitor with water, what will happen? 1. 2. 3. 4. Nothing The thing will blow up. The capacitance will change. The battery will discharge.

Not a fair question o o All answers = 3 points. Let’s check it out.

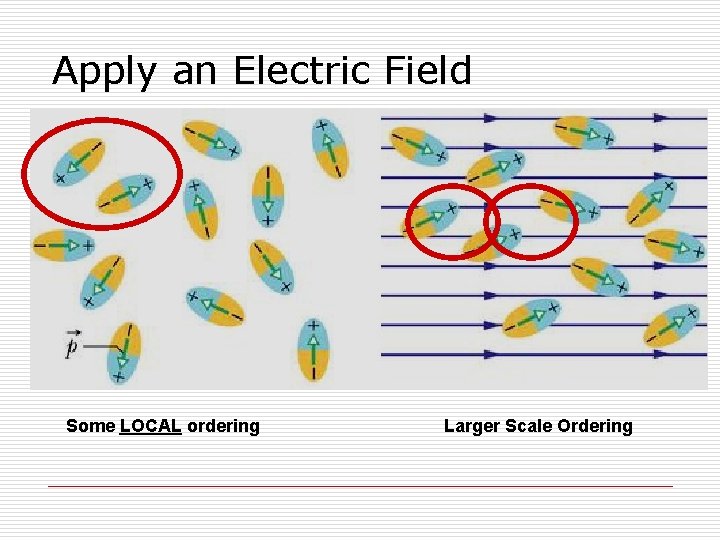
Apply an Electric Field Some LOCAL ordering Larger Scale Ordering

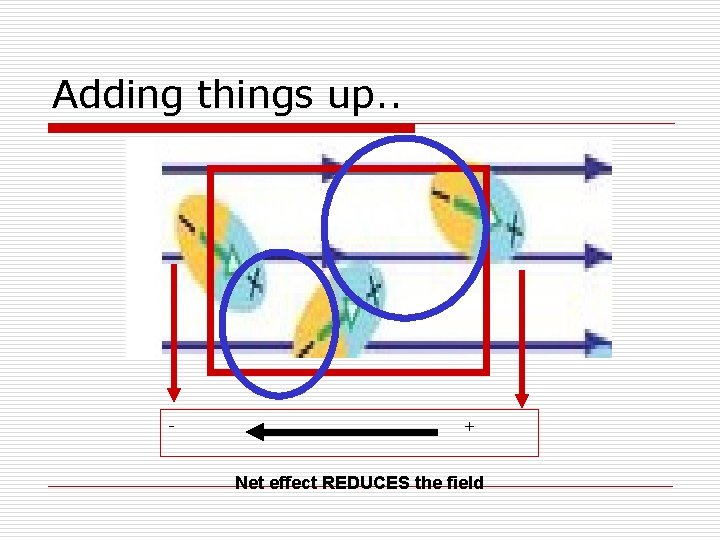
Adding things up. . - + Net effect REDUCES the field

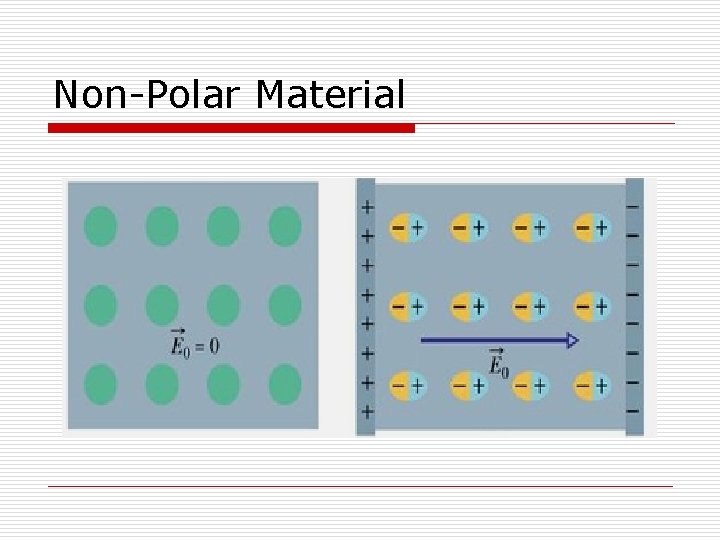
Non-Polar Material

Non-Polar Material Effective Charge is REDUCED

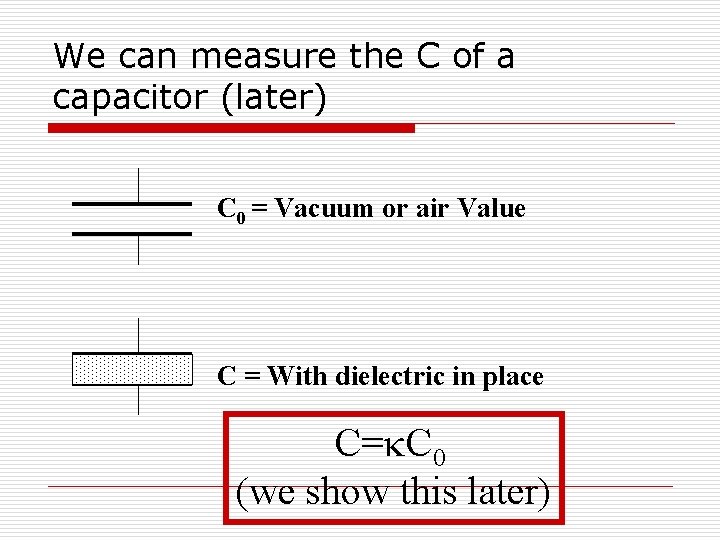
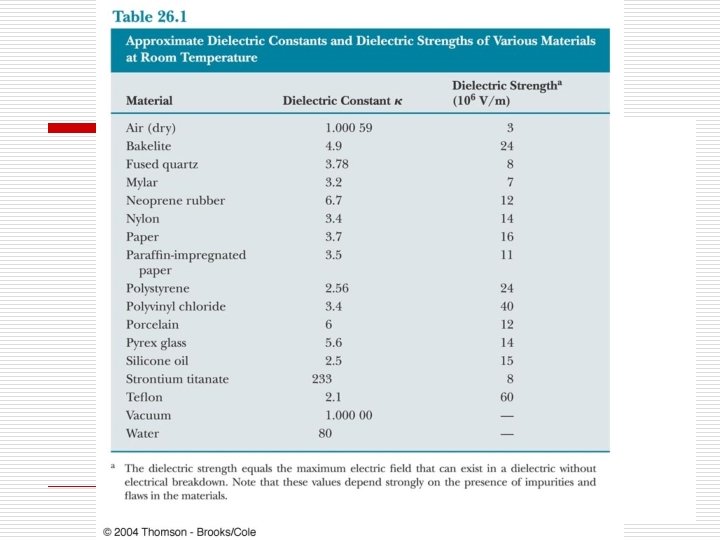
We can measure the C of a capacitor (later) C 0 = Vacuum or air Value C = With dielectric in place C=k. C 0 (we show this later)

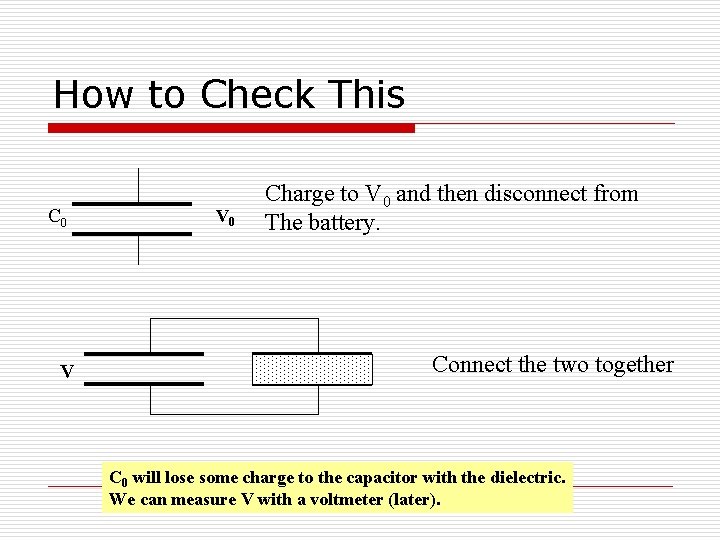
How to Check This C 0 V V 0 Charge to V 0 and then disconnect from The battery. Connect the two together C 0 will lose some charge to the capacitor with the dielectric. We can measure V with a voltmeter (later).

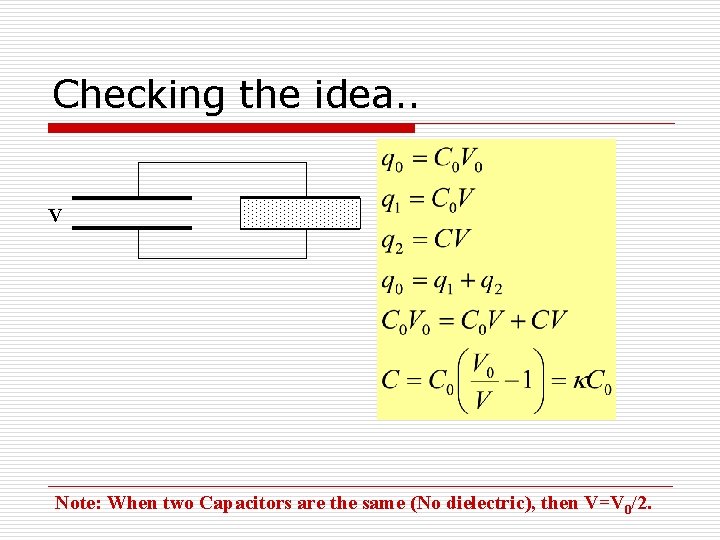
Checking the idea. . V Note: When two Capacitors are the same (No dielectric), then V=V 0/2.

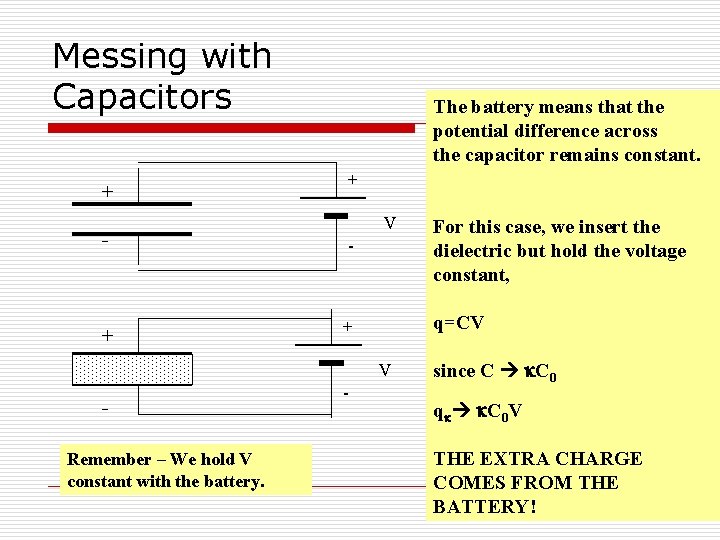
Messing with Capacitors + The battery means that the potential difference across the capacitor remains constant. + V - - For this case, we insert the dielectric but hold the voltage constant, + + q=CV V Remember – We hold V constant with the battery. - since C k. C 0 qk k. C 0 V THE EXTRA CHARGE COMES FROM THE BATTERY!

Another Case o o We charge the capacitor to a voltage V 0. We disconnect the battery. We slip a dielectric in between the two plates. We look at the voltage across the capacitor to see what happens.

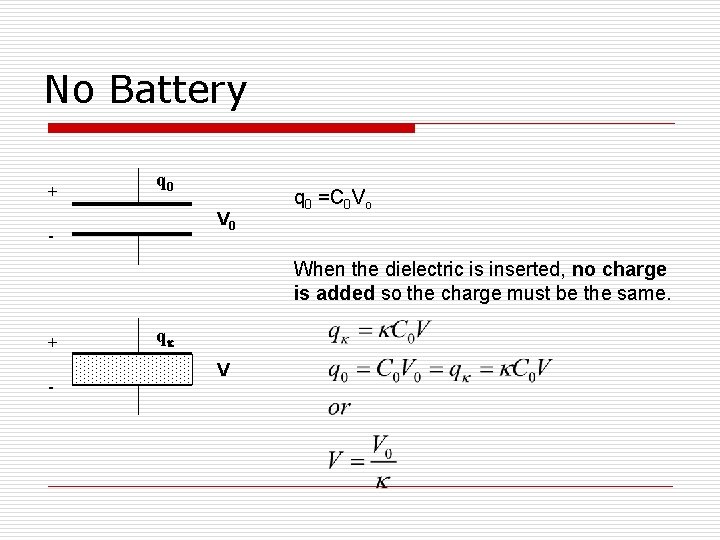
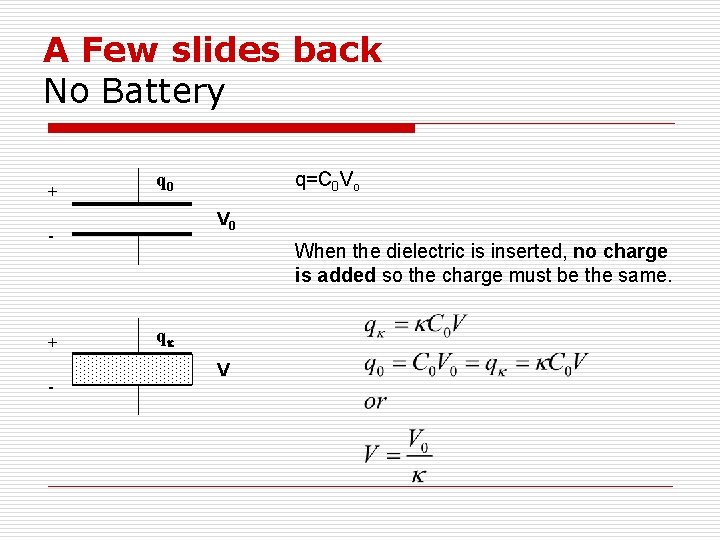
No Battery + q 0 V 0 - q 0 =C 0 Vo When the dielectric is inserted, no charge is added so the charge must be the same. + - qk V

Another Way to Think About This o o There is an original charge q on the capacitor. If you slide the dielectric into the capacitor, you are adding no additional STORED charge. Just moving some charge around in the dielectric material. If you short the capacitors with your fingers, only the original charge on the capacitor can burn your fingers to a crisp! The charge in q=CV must therefore be the free charge on the metal plates of the capacitor.

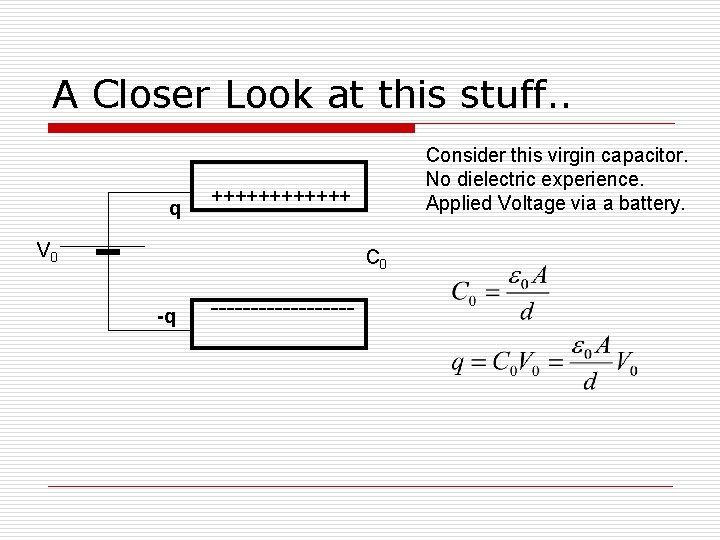
A Closer Look at this stuff. . q Consider this virgin capacitor. No dielectric experience. Applied Voltage via a battery. ++++++ V 0 C 0 -q ---------

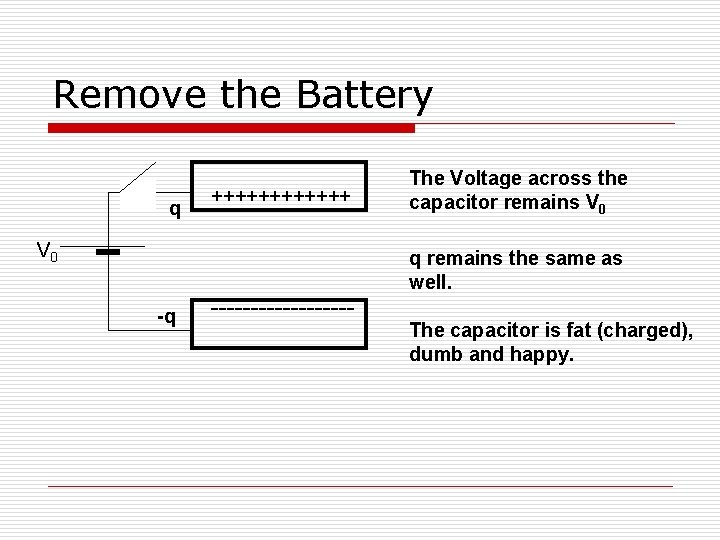
Remove the Battery q ++++++ V 0 The Voltage across the capacitor remains V 0 q remains the same as well. -q --------- The capacitor is fat (charged), dumb and happy.

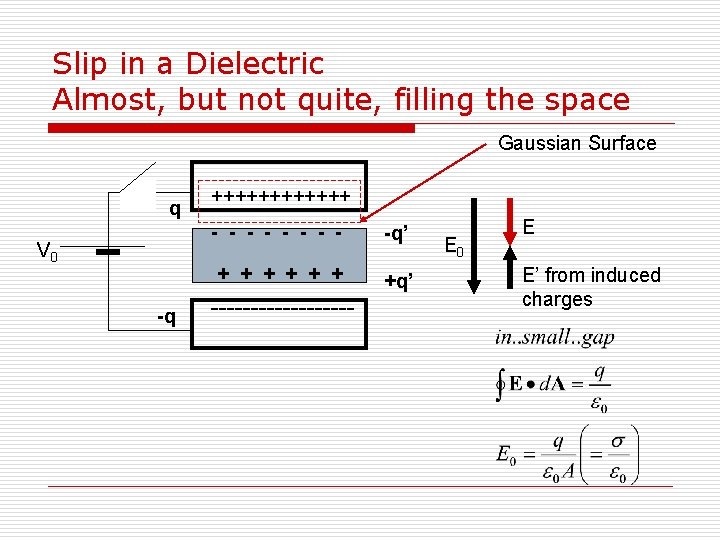
Slip in a Dielectric Almost, but not quite, filling the space Gaussian Surface q V 0 -q ++++++ - - - - -q’ + + + +q’ --------- E 0 E E’ from induced charges

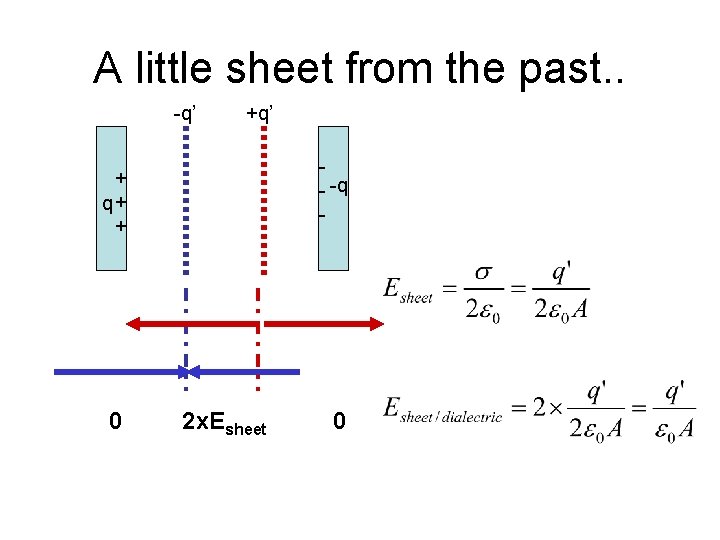
A little sheet from the past. . -q’ +q’ - -q - + q+ + 0 2 x. Esheet 0

Some more sheet…

A Few slides back No Battery + V 0 - + - q=C 0 Vo q 0 When the dielectric is inserted, no charge is added so the charge must be the same. qk V

From this last equation

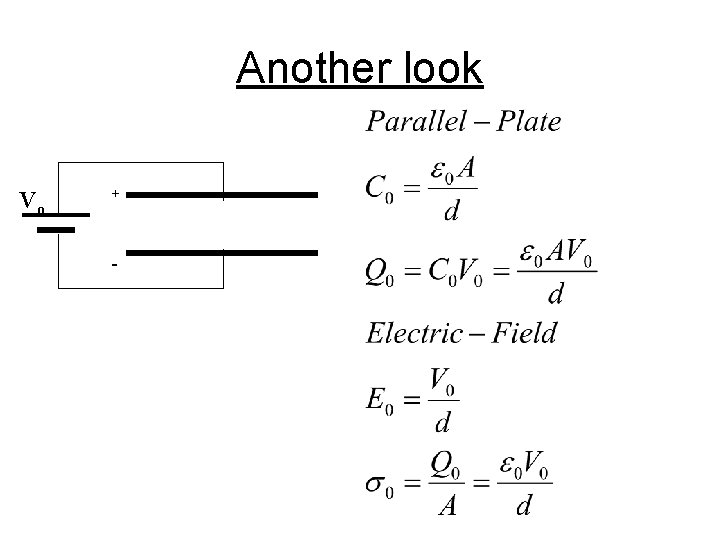
Another look Vo + -

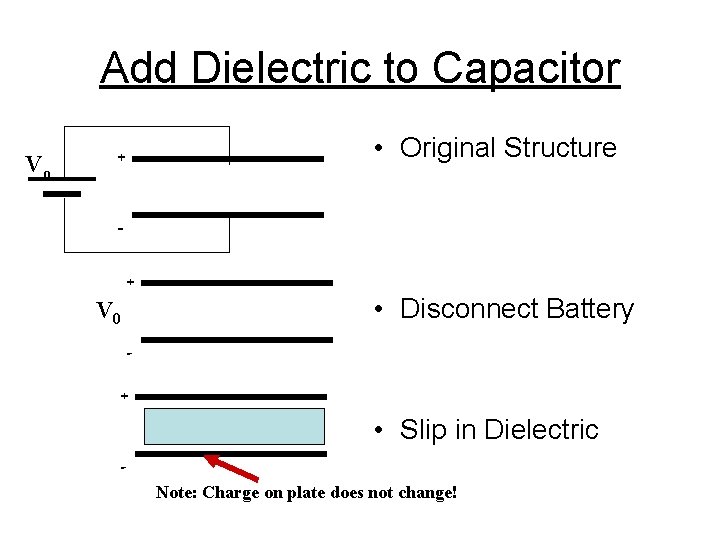
Add Dielectric to Capacitor Vo • Original Structure + - V 0 + • Disconnect Battery + • Slip in Dielectric - Note: Charge on plate does not change!

What happens? so + so - si + si Potential Difference is REDUCED by insertion of dielectric. Charge on plate is Unchanged! Capacitance increases by a factor of k as we showed previously

SUMMARY OF RESULTS

APPLICATION OF GAUSS’ LAW

New Gauss for Dielectrics